График на функција

График на функција f е збир од сите подредени парови (x, f(x)), каде нивната функционална врска е претставена графички^[1]. Ако x е реален број, графикот дава ликовна претстава на овој збир, во облик на крива на координатна рамнина со оски. Доколку аргументот x е подреден пар (x₁, x₂) од реални броеви, графикот е збир од сите подредени тројки (x₁, x₂, f(x₁, x₂)), и графички се претставува како површина.

Графикот на функцијата на реални броеви е ист со графичката претстава на функцијата. Кај општите функции не може да се примени графичка претстава, п затпа формалната дефиниција на графикот на функцијата одговара на потребите на математичките искази, како на пр. теоремата за затворениот график во функционалната анализа.

Поимањето за график на функција се воопштува во график на релација. Иако една функција е секогаш во потесна врска со нејзиниот график, тие не се исти бидејќи се случува две функции со различен кодомен да имаат ист график. На пример, долуспоменатиот кубен полином е сурјекција ако неговиот кодомен се реалните броеви, но не ако кодоменот му е комплексното поле.

Графиките наоѓаат широка примена во науката, инженерството, технологијата, економијата и други области, за претставување на информации, состојби и трендови.

Примери

График на функцијата f(x)=x³ - 9x

Функции со една променлива

График на функцијата

${\displaystyle f(x)=\left\{{\begin{matrix}0,&{\mbox{if }}x<0\\2x,&{\mbox{if }}0<x<1\\0,&{\mbox{if }}x>1.\end{matrix}}\right.}$

е

{(x<0,0), (0<x<1,2x), (x>1,0)}.

Графикот на кубниот полином со една променлива

${\displaystyle f(x)={(x<0,0)}\!\ }$

е

{(x, x³-9x) : x е реален број}.

Ако множеството го исцртаме на Декартова рамнина, добиваме крива.

График на функцијата f(x, y) = sin(x²)·cos(y²).

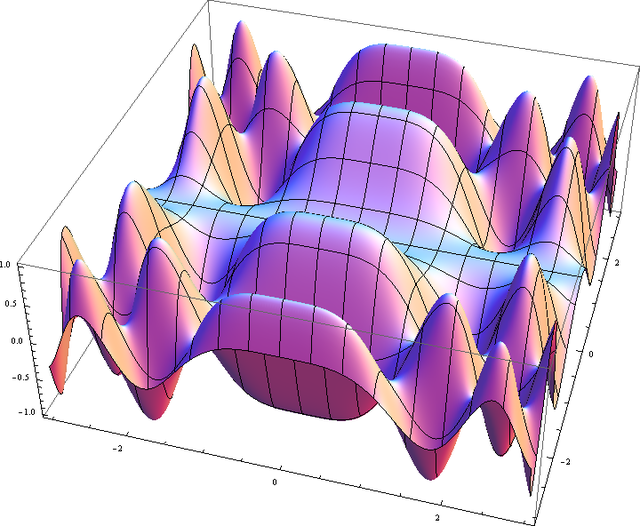
Функции со две променливи

Графот на тригонометриска функција на реалната бројна оска

f(x, y) = sin(x²)·cos(y²)

е

{(x, y, sin(x²)·cos(y²)) : x е реален број}.

Ако множеството го исцртаме во тридимензионални координати, добиваме површина.

Поврзано

• Граф
• Извод од функција
• Транслација (математика)
• Извод на имплицитна функција
• Извод на сложена функција

Наводи

1. Андреевски, Венцислав П. (2007). „4.9. Функции“. Прирачник за математички поими и формули. Скопје: Винсент графика. стр. 89. ISBN 978-9989-2474-4-6.

Надворешни врски

„График на функција“ на Ризницата ?

„График на функција“ од Ерик В. Вајсштајн — MathWorld (англиски)

• Портал: Математика