Numerus realis

Numerus realis^[1] est numerus ullus qui punctis decimalibus infinitis scribatur, sicut 9.73985647892038457. . . . Includuntur numeri rationales sicut 42 et −23/129, et irrationales sicut π et radices quadratae. Copia de numeri reales ${\displaystyle \mathbb {R} }$ aut ${\displaystyle \mathbf {R} }$ notatur.

Linea numerorum

Systemata Numerica Mathematicae

Numeri Elementarii
Naturales ${\displaystyle \mathbb {N} }$ {0,1,2,3,...} sive {1,2,3,...} Primi ${\displaystyle \mathbb {P} }$ {2,3,5,7,11,...} Abundantes Amicabiles Compositi Defectivi Perfecti Sociabiles Integri ${\displaystyle \mathbb {Z} }$ {...,-2,-1,0,+1,+2,...} Pares {...,-2,0,+2,...} Impares {...,-3,-1,+1,+3,...} Rationales ${\displaystyle \mathbb {Q} }$ Reales ${\displaystyle \mathbb {R} }$ Irrationales Complexi ℂ Algebraici Transcendentes Numerus pi ${\displaystyle \pi =3.14159265358979\ldots }$ Numerus Euleri ${\displaystyle e=2.718281828459045\ldots }$ Numerus imaginarius ${\displaystyle i={\sqrt {-1}}}$ Quaterni ${\displaystyle \mathbb {H} }$ Octoni ${\displaystyle \mathbb {O} }$ Infinitas ${\displaystyle \infty }$
Variae radices
Radix binaria(2) Radix octalis(8) Radix decimalis(10) Radix sedecimalis(16)

Puncta lineae infinitae numeros reales repraesentant: numeri positivi ad dexteram partem, negativi ad sinistram; numeri quorum magnitudo maior sit longior absunt ab puncto quod zero repraesentat.

Numeri integri (... -3, -2, -1, 0, 1, 2, 3, ...) punctis repraesentantur quae intervallis aequis inter se distant. Numeri rationales inter puncta integralia sunt; tanti rationales sunt quanti sunt integri. Plures autem numeri irrationales sunt quam rationales.

Numerus irrationalis ${\displaystyle {\sqrt {2}}}$ inter duas copias rationalium. Numeri rubri quadratum < 2 habent; numeri caeruli quadratum > 2 habent.

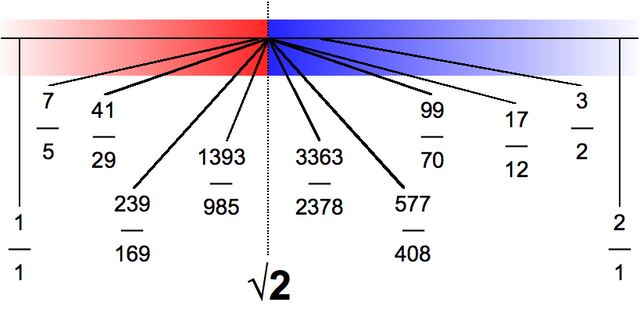
Numeri rationales sunt rationes vel fractiones. Numeri irrationales (per definitionem) non sunt. Definitio numeri cuiusdam irrationalis est limes sequentiae numerorum rationalium; haec est repraesentatio decimalis. Definitio analytica sectione Dedekind utitur. Sectio Dedekind numeri realis X est divisio numerorum rationalium in duas partes, quarum una, pars sinistra, omnes numeros < X continet, altera, pars dextra, omnes numeros > X. Si X = ${\displaystyle {\sqrt {2}}}$, copia sinistra sectionis Dedekind X continet 1, 13/10, 239/169, 1393/185, etc. Copia dextra continet 3/2, 3363/2378, etc.

Notae

1. Renatus Cartesius, Geometria III p. 76. "Quemadmodum, tametsi tres imaginari possimus in hac, x3—6xx+13x—10 = 0; tamen una tantùm est realis; nempe 2; et quod ad reliquas duas attinet, quamvis illae augeantur, diminuantur, aut multiplicentur, sicut iam exposui; tamen non nisi imaginariae fieri possunt.

Bibliographia

• Cantor, Georg. 1874. "Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen". Journal für die Reine und Angewandte Mathematik 77: 258–62.
• Feferman, Solomon. 1989. The Number Systems: Foundations of Algebra and Analysis, AMS Chelsea. ISBN 0-8218-2915-7.
• Katz, Robert. 1964. Axiomatic Analysis. D.C. Heath and Company.
• Landau, Edmund. 2001. Foundations of Analysis. American Mathematical Society. ISBN 0-8218-2693-X.
• Howie, John M. 2005. Real Analysis. Springer. ISBN 1-85233-314-6.
• Schumacher, Carol. 1996. ChapterZero: Fundamental Notions of Abstract Mathematics. Addison-Wesley. ISBN 978-0-201-82653-1.

Nexus externi

• Numeri reales: Pythagoras ad Stevin (Anglice)
• Numeri reales: Stevin ad Hilbertum (Anglice)
• Numeri reales: Intellegere (Anglice)