반사 (기하학)

기하학에서 반사(反射, 영어: reflection) 또는 대칭 이동(對稱 移動)은 유클리드 공간 위의 점을 어떤 초평면에 대한 ‘거울상’으로 변환시키는 함수이다.

정의

유클리드 공간 ${\displaystyle \mathbb {R} ^{n}}$의 ${\displaystyle (n-1)}$차원 부분 아핀 공간 ${\displaystyle \operatorname {Fix} (R)\subset \mathbb {R} ^{n}}$을 반사 초평면으로 하는 반사

${\displaystyle R\colon \mathbb {R} ^{n}\to \mathbb {R} ^{n}}$

는 다음과 같다.

• 임의의 ${\displaystyle \mathbf {x} \in \mathbb {R} ^{n}}$에 대하여, ${\displaystyle R(\mathbf {x} )}$는 ${\displaystyle \operatorname {Fix} (R)}$가 선분 ${\displaystyle (\mathbf {x} ,R(\mathbf {x} ))}$의 수직 이등분 초평면이 되게 만드는 유일한 점이다.

반사 초평면의 점 ${\displaystyle \mathbf {x} _{0}}$ 및 단위 법벡터 ${\displaystyle \mathbf {n} }$이 주어졌을 때, 이는 다음과 같이 나타낼 수 있다.

${\displaystyle R(\mathbf {x} )=\mathbf {x} -2((\mathbf {x} -\mathbf {x} _{0})\cdot \mathbf {n} )\mathbf {n} }$

성질

모든 반사는 유클리드 공간의 등거리 변환이며, 방향을 보존하지 않는다. 특히, 모든 반사는 아핀 변환이며, 선형 변환 성분의 행렬식은 −1이다. 원점을 지나는 반사 초평면을 갖는 반사는 선형 변환이다. 모든 반사는 대합이다. 즉, 스스로를 두 번 합성하면 항등 함수를 얻는다.

고정점

반사의 고정점의 집합은 반사 초평면이다.

연산에 대한 닫힘

반사 ${\displaystyle R}$의 등거리 변환 ${\displaystyle I}$에 의한 켤레 역시 반사이며, 그 반사 초평면은 다음과 같다.

${\displaystyle \operatorname {Fix} (I\circ R\circ I^{-1})=I(\operatorname {Fix} (R))}$

행렬 표현

반사의 선형 변환 성분은 적절한 기저에 대하여 다음과 같은 행렬 표현을 갖는다.

${\displaystyle {\begin{pmatrix}1\\&\ddots \\&&1\\&&&-1\end{pmatrix}}}$

합성

평면 위에서, 평행하는 두 직선을 축으로 하여 연이어 반사하면 평행 이동을 얻는다.

평면 위에서, 교차하는 두 직선을 축으로 하여 연이어 반사하면 회전을 얻는다.

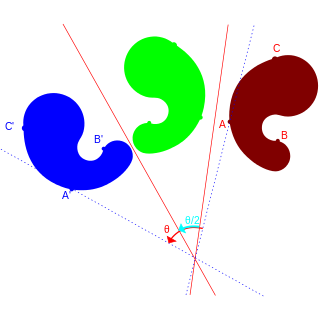
평행하는 반사 초평면을 갖는 두 반사 ${\displaystyle R}$, ${\displaystyle R'}$의 합성 ${\displaystyle R'\circ R}$은 평행 이동이며, (${\displaystyle R}$의 반사 초평면에서 ${\displaystyle R'}$의 반사 초평면을 향하는) 공통 법벡터의 방향으로 반사 초평면 사이 거리의 2배만큼 평행 이동한다. 즉, 만약

${\displaystyle \operatorname {Fix} (R)=\{\mathbf {x} \in \mathbb {R} ^{n}\colon (\mathbf {x} -\mathbf {x} _{0})\cdot \mathbf {n} =0\}}$

${\displaystyle \operatorname {Fix} (R')=\{\mathbf {x} \in \mathbb {R} ^{n}\colon (\mathbf {x} -\mathbf {x} _{0}')\cdot \mathbf {n} =0\}}$

${\displaystyle \|\mathbf {n} \|=1}$

이라면, ${\displaystyle R'\circ R}$의 평행 이동 벡터는

${\displaystyle 2(\mathbf {x} _{0}'-\mathbf {x} _{0})\cdot \mathbf {n} }$

이다. 반대로, 모든 평행 이동은 이러한 두 반사의 합성으로 나타낼 수 있다.

교차하는 반사 초평면을 갖는 두 반사 ${\displaystyle R}$, ${\displaystyle R'}$의 합성 ${\displaystyle R'\circ R}$은 회전이다. 구체적으로, 이 회전은 두 반사 초평면의 교집합을 고정점 집합으로 가지며, 고정점 집합과 수직인 각 평면으로 제한되었을 때 두 반사 초평면 사이의 각의 2배만큼 (${\displaystyle R}$에서 ${\displaystyle R'}$을 향하여) 회전시킨다. 즉, 만약

${\displaystyle \operatorname {Fix} (R)=\{\mathbf {x} \in \mathbb {R} ^{n}\colon (\mathbf {x} -\mathbf {x} _{0})\cdot \mathbf {n} =0\}}$

${\displaystyle \operatorname {Fix} (R')=\{\mathbf {x} \in \mathbb {R} ^{n}\colon (\mathbf {x} -\mathbf {x} _{0}')\cdot \mathbf {n} '=0\}}$

${\displaystyle \|\mathbf {n} \|=\|\mathbf {n} '\|=1}$

${\displaystyle \mathbf {n} \times \mathbf {n} '\neq 0}$

이라면, ${\displaystyle R'\circ R}$의 고정점 집합은

${\displaystyle \operatorname {Fix} (R)\cap \operatorname {Fix} (R')}$

이다. 또한, 평면 ${\displaystyle \mathbf {x} _{0}+(\operatorname {Fix} (R)\cap \operatorname {Fix} (R'))^{\perp }}$ (${\displaystyle \mathbf {x} _{0}\in \operatorname {Fix} (R)\cap \operatorname {Fix} (R')}$)로 제한되었을 때, 회전

${\displaystyle R'\circ R\upharpoonright (\mathbf {x} _{0}+(\operatorname {Fix} (R)\cap \operatorname {Fix} (R'))^{\perp })}$

의 회전 중심은 ${\displaystyle \mathbf {x} _{0}}$이며, 회전 각도는

${\displaystyle 2\arccos(\mathbf {n} \cdot \mathbf {n} ')}$

이다. 반대로, 3차원 이하 유클리드 공간 위의 회전은 두 반사의 합성으로 나타낼 수 있다. 그러나 이는 4차원부터는 성립하지 않는다.

사원수 표현

3차원 벡터를 순허수 사원수로 여겼을 때, ${\displaystyle \mathbb {R} ^{3}}$ 위의 반사는 사원수 곱셈을 통해 간단하게 나타낼 수 있다. 구체적으로, 점 ${\displaystyle \mathbf {x} _{0}}$을 지나며 단위 법벡터 ${\displaystyle \mathbf {n} }$을 갖는 초평면 ${\displaystyle \operatorname {Fix} (R)\subset \mathbb {R} ^{3}}$에 대한 반사는 다음과 같이 나타낼 수 있다.

${\displaystyle R(\mathbf {x} )=\mathbf {x} _{0}+\mathbf {n} (\mathbf {x} -\mathbf {x} _{0})\mathbf {n} }$

여기서 우변의 곱셈은 사원수의 곱셈이다.

예

2차원 유클리드 공간 ${\displaystyle \mathbb {R} ^{2}}$ 위의 x축 및 y축에 대한 반사는 각각 다음과 같다.

${\displaystyle {\begin{pmatrix}x\\y\end{pmatrix}}\mapsto {\begin{pmatrix}1&0\\0&-1\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}x\\-y\end{pmatrix}}}$

${\displaystyle {\begin{pmatrix}x\\y\end{pmatrix}}\mapsto {\begin{pmatrix}-1&0\\0&1\end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}}={\begin{pmatrix}-x\\y\end{pmatrix}}}$

같이 보기

• 덧셈 역원
• 하우스홀더 변환
• 반전기하학

외부 링크

• “Reflection”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
• Weisstein, Eric Wolfgang. “Reflection”. 《Wolfram MathWorld》 (영어). Wolfram Research.