리 군 이론에서, 근계 (根系, 영어 : root system )는 일련의 기하학적 성질을 만족하는 유한 차원 벡터 의 집합 이다. 근계의 원소인 벡터는 근 (根, 영어 : root )이라고 부른다. 주어진 근계에 대하여 특정 성질을 만족하는 부분집합인 단순근 (單純根, 영어 : simple root )의 집합을 고를 수 있고, 이를 딘킨 도표 (영어 : Dynkin diagram )로 나타내어 분류할 수 있다. 반단순 리 군 에 근계를 대응시킬 수 있으며, 이를 통해 반단순 리 군들을 분류할 수 있다.
이 문서는 수학에서
리 대수 를 분류하는 벡터의 집합에 관한 것입니다.
식물학 에서 식물의 뿌리들의 구조에 대해서는
뿌리 문서를, 대한민국의 지명에 대해서는
근계리 문서를 참고하십시오.
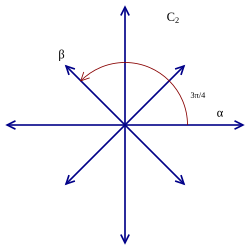
예외 리 군 G2 의 근계.
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
모든 근계는 기약 근계 (旣約根系, 영어 : irreducible root system )의 합으로 나타낼 수 있다. 기약 근계(의 동형류)는 복소수체 위의 단순 리 대수 (의 동형류)와 일대일로 대응한다.
유한 차원 실수 내적 공간
(
V
,
(
⋅
,
⋅
)
)
{\displaystyle (V,(\cdot ,\cdot ))}
Φ
⊆
V
{\displaystyle \Phi \subseteq V}
근계 라고 한다.
(선형 생성)
V
=
Span
R
Φ
{\displaystyle V=\operatorname {Span} _{\mathbb {R} }\Phi }
V
{\displaystyle V}
Φ
{\displaystyle \Phi }
선형 결합 으로 나타낼 수 있다. (이는 유일하지 않을 수 있다.)
(스칼라배의 제한)
α
∈
Φ
{\displaystyle \alpha \in \Phi }
−
α
∈
Φ
{\displaystyle -\alpha \in \Phi }
t
Φ
{\displaystyle t\Phi }
t
∈
R
{\displaystyle t\in \mathbb {R} }
Φ
{\displaystyle \Phi }
(반사에 대한 닫힘) 임의의
α
,
β
∈
Φ
{\displaystyle \alpha ,\beta \in \Phi }
α
{\displaystyle \alpha }
β
{\displaystyle \beta }
β
−
2
α
(
α
,
β
)
/
(
α
,
α
)
{\displaystyle \beta -2\alpha (\alpha ,\beta )/(\alpha ,\alpha )}
Φ
{\displaystyle \Phi }
(정수성)
0
∉
Φ
{\displaystyle 0\not \in \Phi }
∀
α
,
β
∈
Φ
:
2
(
α
,
β
)
/
(
α
,
α
)
∈
Z
{\displaystyle \forall \alpha ,\beta \in \Phi \colon 2(\alpha ,\beta )/(\alpha ,\alpha )\in \mathbb {Z} }
유한 집합 이다.근계의 원소는 근 이라고 부른다. 근계의 계수 (階數, 영어 : rank )는
V
{\displaystyle V}
두 실수 내적 공간
V
{\displaystyle V}
V
′
{\displaystyle V'}
Φ
⊆
V
{\displaystyle \Phi \subseteq V}
Φ
′
⊆
V
′
{\displaystyle \Phi '\subseteq V'}
f
(
Φ
)
=
Φ
′
{\displaystyle f(\Phi )=\Phi '}
전단사 실수 선형 변환
f
:
V
→
V
′
{\displaystyle f\colon V\to V'}
(
f
(
α
)
,
f
(
β
)
)
V
′
(
f
(
α
)
,
f
(
α
)
)
V
′
=
(
α
,
β
)
V
(
α
,
α
)
V
∀
α
,
β
∈
Φ
{\displaystyle {\frac {(f(\alpha ),f(\beta ))_{V'}}{(f(\alpha ),f(\alpha ))_{V'}}}={\frac {(\alpha ,\beta )_{V}}{(\alpha ,\alpha )_{V}}}\qquad \forall \alpha ,\beta \in \Phi }
라면,
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
(
V
′
,
Φ
′
)
{\displaystyle (V',\Phi ')}
동형
특히, 동형이 등거리 변환 일 필요는 없다. 예를 들어, 항등 함수
(
V
,
(
−
,
−
)
)
→
(
V
,
2
(
−
,
−
)
)
{\displaystyle (V,(-,-))\to (V,2(-,-))}
노름 을
2
{\displaystyle {\sqrt {2}}}
1
{\displaystyle 1}
2
/
3
{\displaystyle {\sqrt {2/3}}}
통상적으로, 다음과 같은 표기를 사용한다.
⟨
α
,
β
⟩
=
2
(
α
,
β
)
(
α
,
α
)
{\displaystyle \langle \alpha ,\beta \rangle ={\frac {2(\alpha ,\beta )}{(\alpha ,\alpha )}}}
(이는 물론 쌍선형 형식 을 이루지 못한다.)
근계
Φ
{\displaystyle \Phi }
양근의 집합 (陽根의 集合, 영어 : set of positive roots )
Φ
+
⊂
Φ
{\displaystyle \Phi ^{+}\subset \Phi }
임의의
α
∈
Φ
{\displaystyle \alpha \in \Phi }
α
∈
Φ
+
{\displaystyle \alpha \in \Phi ^{+}}
−
α
∈
Φ
+
{\displaystyle -\alpha \in \Phi ^{+}}
{
α
,
−
α
}
⊂
Φ
+
{\displaystyle \{\alpha ,-\alpha \}\subset \Phi ^{+}}
α
,
β
∈
Φ
+
{\displaystyle \alpha ,\beta \in \Phi ^{+}}
α
+
β
∈
Φ
{\displaystyle \alpha +\beta \in \Phi }
α
+
β
∈
Φ
+
{\displaystyle \alpha +\beta \in \Phi ^{+}}
양근의 집합의 원소를 양근 (陽根, 영어 : positive root )이라고 한다. 양근의 집합
Φ
+
⊆
Φ
{\displaystyle \Phi ^{+}\subseteq \Phi }
{
v
∈
V
:
∀
α
∈
Φ
:
α
∨
(
v
)
∈
Z
}
{\displaystyle \{v\in V\colon \forall \alpha \in \Phi \colon \alpha ^{\vee }(v)\in \mathbb {Z} \}}
위에 다음과 같은 부분 순서 를 줄 수 있다.
u
≤
v
⟺
∀
α
∈
Φ
+
:
α
∨
(
v
−
u
)
≥
0
{\displaystyle u\leq v\iff \forall \alpha \in \Phi ^{+}\colon \alpha ^{\vee }(v-u)\geq 0}
이 구성은 리 대수 의 표현론 에 등장하며, 이 경우 위의 격자는 정수 무게 의 격자에 해당한다.
어떤 양근의 집합이 주어졌을 때, 단순근 (單純根, 영어 : simple root )은 두 양근의 합으로 나타낼 수 없는 근이다. 단순근들의 집합은
V
{\displaystyle V}
기저 를 이룬다.
근계
Φ
{\displaystyle \Phi }
단순근 의 열
α
1
,
…
,
α
r
{\displaystyle \alpha _{1},\dots ,\alpha _{r}}
카르탕 행렬 (영어 : Cartan matrix )
M
{\displaystyle M}
r
×
r
{\displaystyle r\times r}
정사각 행렬 이다.
M
=
(
M
i
j
)
i
,
j
=
1
,
…
,
r
{\displaystyle M=(M_{ij})_{i,j=1,\dots ,r}}
M
i
j
=
2
(
α
i
,
α
j
)
(
α
i
,
α
i
)
{\displaystyle M_{ij}=2{\frac {(\alpha _{i},\alpha _{j})}{(\alpha _{i},\alpha _{i})}}}
정의에 따라, 카르탕 행렬의 대각선 성분의 값은 모두 2이다.
카르탕 행렬이 주어지면, 이에 대응하는 근계 (및 복소수 반단순 리 대수 )를 재구성할 수 있다.
기약근계의 딘킨 도표 각 근계
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
딘킨 도표 (Дынкин圖表, 영어 : Dynkin diagram )라는, 일종의 유향 그래프 를 대응시킬 수 있다. 우선, 임의로
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
Φ
+
⊆
Φ
{\displaystyle \Phi ^{+}\subseteq \Phi }
딘킨 도표는 각 단순근에 대응하는 꼭짓점 을 갖는다.
두 꼭짓점 사이에는 0개, 1개, 2개, 또는 3개의 변(邊)이 존재할 수 있다. 변이 2개 또는 3개인 경우, 변은 방향을 가지며, 이 방향은 항상 더 짧은 단순근을 가리킨다. (이 경우 두 단순근의 길이는 항상 다르다.)
두 꼭짓점 사이의 변의 수는 두 단순근 사이의 각도에 대응하며, 다음 표를 따른다. 딘킨 도표는 단순근의 선택에 관계없이 동일하다.
기약 근계의 딘킨 도표는 연결되어 있다. 딘킨 도표의 연결 성분 분해는 근계의 (기약 근계들로의) 직합 분해와 같다.
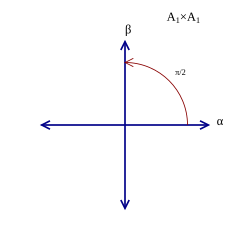
정수성 공리에 따라, 두 근 사이의 각은
π
/
2
{\displaystyle \pi /2}
π
/
3
{\displaystyle \pi /3}
π
/
4
{\displaystyle \pi /4}
π
/
6
{\displaystyle \pi /6}
근계의 정수성은 두 근 사이의 각들을 제한한다. 정수성 공리에 따라, 두 근 사이의 각의 코사인 은 정수의 제곱근의 반이어야 한다.
Z
∋
2
(
α
,
β
)
(
α
,
α
)
⋅
2
(
α
,
β
)
(
β
,
β
)
=
4
(
α
,
β
)
2
|
α
|
2
|
β
|
2
=
4
cos
2
(
θ
)
=
(
2
cos
(
θ
)
)
2
.
{\displaystyle \mathbb {Z} \ni 2{\frac {(\alpha ,\beta )}{(\alpha ,\alpha )}}\cdot 2{\frac {(\alpha ,\beta )}{(\beta ,\beta )}}=4{\frac {(\alpha ,\beta )^{2}}{\vert \alpha \vert ^{2}\vert \beta \vert ^{2}}}=4\cos ^{2}(\theta )=(2\cos(\theta ))^{2}.}
2
cos
(
θ
)
∈
[
−
2
,
2
]
{\displaystyle 2\cos(\theta )\in [-2,2]}
cos
θ
=
0
,
±
1
2
,
±
2
2
,
±
3
2
,
±
1
{\displaystyle \cos \theta =0,\pm {\tfrac {1}{2}},\pm {\tfrac {\sqrt {2}}{2}},\pm {\tfrac {\sqrt {3}}{2}},\pm 1}
이다. 즉,
θ
{\displaystyle \theta }
두 근계
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
(
V
′
,
Φ
′
)
{\displaystyle (V',\Phi ')}
직합
Φ
⊕
Φ
′
{\displaystyle \Phi \oplus \Phi '}
Φ
⊕
Φ
′
=
ι
(
Φ
)
∪
ι
′
(
Φ
′
)
{\displaystyle \Phi \oplus \Phi '=\iota (\Phi )\cup \iota '(\Phi ')}
V
→
ι
V
⊕
V
′
←
ι
′
V
′
{\displaystyle V{\xrightarrow {\iota }}V\oplus V'{\xleftarrow {\iota '}}V'}
여기서
ι
{\displaystyle \iota }
ι
′
{\displaystyle \iota '}
직합 의 정의에 등장하는 표준 포함 사상이다.
기약 근계 (旣約根系, 영어 : irreducible root system )는 두 (자명하지 않은) 근계의 합이 아닌, 자명하지 않은 근계다. 모든 근계는 기약 근계의 합으로 유일하게 나타낼 수 있다.
기약 근계의 근은 모두 길이가 같거나, 길이가 두 가지가 있다. 길이가 두 가지가 있을 경우는 긴 것은 긴 근 (영어 : long root ), 짧은 것은 짧은 근 (영어 : short root )으로 분류한다. (만약 길이가 모두 같다면, 모든 근이 긴 근이다.) 이 경우, 긴 근과 짧은 근의 노름 의 비는
2
{\displaystyle {\sqrt {2}}}
2
{\displaystyle {\sqrt {2}}}
1
{\displaystyle 1}
근계
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
쌍대 근계 (雙對根系, 영어 : dual root system )는 다음과 같다.
V
∨
{\displaystyle V^{\vee }}
V
{\displaystyle V}
쌍대 공간 이다. 물론, 내적을 사용하여 표준적인 동형 사상
V
→
V
∨
{\displaystyle V\to V^{\vee }}
Φ
∨
=
{
α
∨
:
α
∈
Φ
}
{\displaystyle \Phi ^{\vee }=\{\alpha ^{\vee }\colon \alpha \in \Phi \}}
임의의
u
,
v
∈
V
{\displaystyle u,v\in V}
u
∨
∈
V
∗
{\displaystyle u^{\vee }\in V^{*}}
u
∨
(
v
)
=
⟨
u
,
v
⟩
=
2
(
u
,
v
)
/
(
u
,
u
)
{\displaystyle u^{\vee }(v)=\langle u,v\rangle =2(u,v)/(u,u)}
그렇다면
(
V
∨
,
Φ
∨
)
{\displaystyle (V^{\vee },\Phi ^{\vee })}
임의의 근계
(
V
,
Φ
)
{\displaystyle (V,\Phi )}
(
V
∨
∨
,
Φ
∨
∨
)
{\displaystyle (V^{\vee \vee },\Phi ^{\vee \vee })}
단순 근계 가운데,
B
n
{\displaystyle B_{n}}
C
n
{\displaystyle C_{n}}
A
n
{\displaystyle A_{n}}
D
n
{\displaystyle D_{n}}
E
6
,
E
7
,
E
8
,
F
4
,
G
2
{\displaystyle E_{6},E_{7},E_{8},F_{4},G_{2}}
기약 근계는 다음과 같이 분류한다. 고전 근계 (영어 : classical root system )는 네 개의 족
A
n
{\displaystyle A_{n}}
B
n
{\displaystyle B_{n}}
C
n
{\displaystyle C_{n}}
D
n
{\displaystyle D_{n}}
예외 근계 (영어 : exceptional root system )
G
2
,
F
4
,
E
6
,
E
7
,
E
8
{\displaystyle G_{2},F_{4},E_{6},E_{7},E_{8}}
고전군 (직교군 , 특수 유니터리 군 , 심플렉틱 군 )의 리 대수 (의 복소화)의 근계이나, 예외 근계는 그렇지 않다. 아래 표에서는 관례를 따라 긴 근의 길이가
2
{\displaystyle {\sqrt {2}}}
[1]
A
n
{\displaystyle A_{n}}
R
n
+
1
{\displaystyle \mathbb {R} ^{n+1}}
α
1
=
(
1
,
−
1
,
0
,
…
,
0
,
0
)
{\displaystyle \alpha ^{1}=(1,-1,0,\dots ,0,0)}
α
2
=
(
0
,
1
,
−
1
,
…
,
0
,
0
)
{\displaystyle \alpha ^{2}=(0,1,-1,\dots ,0,0)}
⋮
{\displaystyle \vdots }
α
n
=
(
0
,
0
,
…
,
1
,
−
1
)
{\displaystyle \alpha ^{n}=(0,0,\dots ,1,-1)}
B
n
{\displaystyle B_{n}}
α
1
=
(
1
,
−
1
,
0
,
…
,
0
,
0
)
{\displaystyle \alpha ^{1}=(1,-1,0,\dots ,0,0)}
α
2
=
(
0
,
1
,
−
1
,
…
,
0
,
0
)
{\displaystyle \alpha ^{2}=(0,1,-1,\dots ,0,0)}
⋮
{\displaystyle \vdots }
α
n
−
1
=
(
0
,
0
,
…
,
1
,
−
1
)
{\displaystyle \alpha ^{n-1}=(0,0,\dots ,1,-1)}
α
n
=
(
0
,
0
,
…
,
0
,
1
)
{\displaystyle \alpha ^{n}=(0,0,\dots ,0,1)}
C
n
{\displaystyle C_{n}}
α
1
=
(
1
,
−
1
,
0
,
…
,
0
,
0
)
{\displaystyle \alpha ^{1}=(1,-1,0,\dots ,0,0)}
α
2
=
(
0
,
1
,
−
1
,
…
,
0
,
0
)
{\displaystyle \alpha ^{2}=(0,1,-1,\dots ,0,0)}
⋮
{\displaystyle \vdots }
α
n
−
1
=
(
0
,
0
,
…
,
1
,
−
1
)
{\displaystyle \alpha ^{n-1}=(0,0,\dots ,1,-1)}
α
n
=
(
0
,
0
,
…
,
0
,
2
)
{\displaystyle \alpha ^{n}=(0,0,\dots ,0,2)}
D
n
{\displaystyle D_{n}}
α
1
=
(
1
,
−
1
,
0
,
…
,
0
,
0
)
{\displaystyle \alpha ^{1}=(1,-1,0,\dots ,0,0)}
α
2
=
(
0
,
1
,
−
1
,
…
,
0
,
0
)
{\displaystyle \alpha ^{2}=(0,1,-1,\dots ,0,0)}
⋮
{\displaystyle \vdots }
α
n
−
1
=
(
0
,
0
,
…
,
1
,
−
1
)
{\displaystyle \alpha ^{n-1}=(0,0,\dots ,1,-1)}
α
n
=
(
0
,
0
,
…
,
1
,
1
)
{\displaystyle \alpha ^{n}=(0,0,\dots ,1,1)}
근계의 이론은 복소수 반단순 리 대수 의 표현론 에서 비롯하였다. 각 반단순 리 대수에는 근계를 대응시킬 수 있으며, 단순 리 대수 에 대응되는 근계는 기약 근계이다.
카르탕 행렬의 개념은 엘리 카르탕 이 도입하였다. 딘킨 도표의 개념은 예브게니 딘킨 이 도입하였다.
이 문서는 수학에서 리 대수를 분류하는 벡터의 집합에 관한 것입니다. 식물학에서 식물의 뿌리들의 구조에 대해서는 뿌리 문서를, 대한민국의 지명에 대해서는 근계리 문서를 참고하십시오.
, 
...
...
.svg)
![{\displaystyle 2\cos(\theta )\in [-2,2]}](http://wikimedia.org/api/rest_v1/media/math/render/svg/9a5c767297a7512c69089c0b49082c5623727b25)
