무게 (표현론)

리 대수 이론에서, 무게(영어: weight)는 리 대수의 표현을 분류하는 일련의 수들이다.

정의

체 ${\displaystyle K}$에 대한 리 대수 ${\displaystyle {\mathfrak {g}}}$의 무게 ${\displaystyle \lambda \in {\mathfrak {g}}^{\vee }}$는 다음 성질을 만족시키는 ${\displaystyle K}$-선형 범함수이다. (여기서 ${\displaystyle (-)^{\vee }}$는 쌍대 공간이다.)

${\displaystyle \lambda ([a,b])=0\qquad \forall a,b\in {\mathfrak {g}}}$

무게는 리 괄호에 대하여 0이므로, 리 대수 ${\displaystyle {\mathfrak {g}}}$의 무게는 그 가환화 ${\displaystyle {\mathfrak {g}}/[{\mathfrak {g}},{\mathfrak {g}}]}$의 무게로 제한될 수 있다. 즉, ${\displaystyle {\mathfrak {g}}}$의 무게는 ${\displaystyle ({\mathfrak {g}}/[{\mathfrak {g}},{\mathfrak {g}}])^{*}}$의 원소를 정의한다.

무게 가군

다음이 주어졌다고 하자.

• 체 ${\displaystyle K}$
• ${\displaystyle K}$-리 대수 ${\displaystyle {\mathfrak {g}}}$
• ${\displaystyle {\mathfrak {g}}}$의 표현 ${\displaystyle {\mathfrak {g}}\to \operatorname {\mathfrak {gl}} (V;K)}$
• ${\displaystyle {\mathfrak {g}}}$의 무게 ${\displaystyle \lambda \in {\mathfrak {g}}^{*}}$

그렇다면, ${\displaystyle V}$ 속의, 무게 ${\displaystyle \lambda }$의 무게 공간(영어: weight space) ${\displaystyle V_{\lambda }}$는 ${\displaystyle V}$의 다음과 같은 부분 공간이다.

${\displaystyle V_{\lambda }=\{v\in V\colon \forall a\in {\mathfrak {g}}\colon av=\lambda (a)v\}}$

${\displaystyle V_{\lambda }\neq \{0\}}$이라면 ${\displaystyle \lambda }$를 ${\displaystyle V}$의 무게라고 하고, 무게 공간의 원소를 무게 벡터(영어: weight vector)라고 한다.

만약 ${\displaystyle V}$가 그 무게 공간들의 직합이라면, ${\displaystyle V}$를 ${\displaystyle {\mathfrak {g}}}$의 무게 가군(-加群, 영어: weight module)이라고 한다.

마찬가지로, 다음을 정의하자. ${\displaystyle V}$ 속의, 무게 ${\displaystyle \lambda }$의 일반화 무게 공간(영어: generalized weight space) ${\displaystyle V_{\lambda }}$는 ${\displaystyle V}$의 다음과 같은 부분 공간이다.^[1]:130

${\displaystyle V_{\lambda }=\{v\in V\colon \forall a\in {\mathfrak {g}}\colon \exists n\in \mathbb {Z} ^{+}\colon (a-\lambda (a))^{n}v=v\}}$

${\displaystyle V_{\lambda }\neq \{0\}}$이라면 ${\displaystyle \lambda }$를 ${\displaystyle V}$의 일반화 무게(영어: generalized weight)라고 하고, 무게 공간의 원소를 일반화 무게 벡터(영어: generalized weight vector)라고 한다. (유한 차원 ${\displaystyle V}$의 경우 사실 항상 ${\displaystyle n=\dim V}$로 잡을 수 있다.)

마찬가지로, 일반화 무게 공간들의 직합으로 표현되는 표현을 일반화 무게 가군(영어: generalized weight module)이라고 한다.

성질

복소수체 위의 유한 차원 멱영 리 대수 ${\displaystyle {\mathfrak {n}}}$의 모든 유한 차원 표현은 항상 일반화 무게 가군이다.^{[1]:130, Proposition II.2.4}

복소수체 위의 유한 차원 아벨 리 대수 ${\displaystyle {\mathfrak {a}}}$의 모든 유한 차원 표현은 항상 무게 가군이다.

반단순 리 대수의 카르탕 부분 대수의 무게

만약 ${\displaystyle {\mathfrak {g}}}$가 복소수체 위의 유한 차원 반단순 리 대수라고 하고, 그 카르탕 부분 대수 ${\displaystyle {\mathfrak {h}}\subseteq {\mathfrak {g}}}$를 고르자. ${\displaystyle [{\mathfrak {g}},{\mathfrak {g}}]={\mathfrak {g}}}$이므로, ${\displaystyle {\mathfrak {g}}}$ 위의 모든 무게는 자명하다. 그러나 아벨 리 대수 ${\displaystyle {\mathfrak {h}}}$는 (물론) 자명하지 않을 수 있다. 이 경우, ${\displaystyle {\mathfrak {g}}}$의 모든 유한 차원 표현은 (${\displaystyle {\mathfrak {h}}}$에 제한되었을 때) ${\displaystyle {\mathfrak {h}}}$의 무게 가군을 이룬다.

딸림표현 ${\displaystyle V={\mathfrak {g}}}$의 ${\displaystyle {\mathfrak {h}}}$-무게들을 ${\displaystyle {\mathfrak {g}}}$의 근(根, 영어: root)이라고 하며, 이들은 ${\displaystyle {\mathfrak {h}}^{*}}$의 벡터들의 집합으로서 근계를 이룬다. 근 ${\displaystyle \lambda }$에 대응하는 쌍대근(雙對根, 영어: coroot) ${\displaystyle \lambda ^{\vee }\in {\mathfrak {h}}}$은

${\displaystyle \lambda ^{\vee }={\frac {2\lambda }{\langle \lambda ,\lambda \rangle }}}$

이다.

단순 리 대수의 무게

${\displaystyle {\mathfrak {g}}}$가 복소수체 위의 유한 차원 단순 리 대수라고 하고, 그 카르탕 부분 대수 ${\displaystyle {\mathfrak {h}}\subseteq {\mathfrak {g}}}$를 고르자. ${\displaystyle {\mathfrak {g}}}$의 정수 무게(整數-, 영어: integral weight) ${\displaystyle \lambda \in {\mathfrak {h}}^{*}}$는 다음 조건을 만족시키는 무게이다.

• 모든 쌍대근 ${\displaystyle \gamma ^{\vee }=2\gamma /\langle \gamma ,\gamma \rangle }$에 대하여, ${\displaystyle \lambda (\gamma ^{\vee })\in \mathbb {Z} }$. (다시 말해, 모든 근 ${\displaystyle \gamma }$에 대하여, ${\displaystyle 2\langle \lambda ,\gamma \rangle /\langle \gamma ,\gamma \rangle \in \mathbb {Z} }$.)

정수 무게들의 집합 ${\displaystyle P({\mathfrak {g}},{\mathfrak {h}})\subseteq \mathbb {h} }$는 (덧셈군으로서) ${\displaystyle \mathbb {Z} ^{\oplus \dim {\mathfrak {h}}}}$와 동형이며, 이를 정수 무게 격자(영어: integral weight lattice)라고 한다.

${\displaystyle {\mathfrak {g}}}$의 근계의 양근 ${\displaystyle \Delta ^{+}({\mathfrak {g}},{\mathfrak {h}})\subseteq \Delta ({\mathfrak {g}},{\mathfrak {h}})}$ 및 이를 생성하는 단순근 ${\displaystyle \operatorname {S} ({\mathfrak {g}},{\mathfrak {h}})\subseteq \Delta ^{+}({\mathfrak {g}},{\mathfrak {h}})}$를 고르자. 그렇다면, ${\displaystyle {\mathfrak {g}}}$의 기본 무게(基本-, 영어: fundamental weight) ${\displaystyle \lambda _{i}}$는 (선택한 양근 집합에 대한) 단순근에 대응되는 쌍대근들의 집합의 쌍대 기저의 원소이다. 즉, 단순근 집합 ${\displaystyle \operatorname {S} ({\mathfrak {g}},{\mathfrak {h}})=(\alpha _{i})_{i\in \{1,\dotsc ,\dim _{\mathbb {h} }\}}}$에 대하여 다음 조건을 만족시키는 무게 ${\displaystyle (\omega _{i})_{i\in \{1,\dotsc ,\dim _{\mathbb {h} }\}}\subseteq {\mathfrak {h}}}$이다.

${\displaystyle 2{\frac {\langle \omega _{i},\alpha _{j}\rangle }{\langle \alpha _{j},\alpha _{j}\rangle }}=\delta _{ij}}$

이에 따라, 정수 무게는 기본 무게의 정수 계수 선형 결합이 된다.

${\displaystyle {\mathfrak {g}}}$의 우세 무게(優勢-, 영어: dominant weight)는 기본 무게의 음이 아닌 실수 계수 선형 결합이다. 즉, 무게 ${\displaystyle \gamma \in {\mathfrak {h}}}$가 우세 무게가 될 필요 충분 조건은 모든 양근 (또는 단순근) ${\displaystyle \alpha }$에 대하여

${\displaystyle \langle \gamma ,\alpha \rangle \geq 0}$

인 것이다. ${\displaystyle {\mathfrak {g}}}$의 우세 정수 무게(優勢-, 영어: dominant integral weight)는 기본 무게들의 음이 아닌 정수 계수의 선형 결합이다. 우세 무게들의 닫힌집합(즉, 우세 정수 무게들의 볼록포)를 기본 바일 방(영어: fundamental Weyl chamber)이라고 한다.

즉, 다음과 같은 포함 관계가 성립한다.

무게	⊃	정수 무게	⊃	근	⊃	양근	⊃	단순근
∪		∪
우세 무게	⊃	우세 정수 무게	⊃	기본 무게
		⟒
		영벡터 (0)

여기서

• 밑줄로 강조된 것들은 양근의 선택에 의존하지만, 나머지는 그렇지 않다.
• 기울어지게 쓰인 것들은 유한 집합이며, 나머지는 무한 집합이다.

예

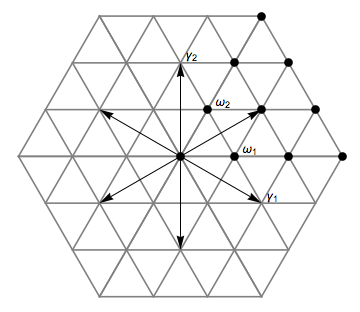
다음과 같은 A₂ 근계를 생각하자.

여기서

• 평면의 모든 점은 무게이다. (즉, 그 수는 비가산 무한 개이다.)
• 삼각형 격자의 모든 꼭짓점은 정수 무게이다. (즉, 그 수는 가산 무한 개이다.)
• 굵게 칠해진 꼭짓점들은 우세 정수 무게이다. (즉, 그 수는 가산 무한 개이다.)
• 굵게 칠해진 꼭짓점들의 볼록포인 60° 부채꼴 속의 점은 우세 무게이다. (즉, 그 수는 비가산 무한 개이다.)
• 화살표의 머리들(${\displaystyle \pm \gamma _{1}}$, ${\displaystyle \pm \gamma _{2}}$, ${\displaystyle \pm (\gamma _{1}+\gamma _{2})}$)은 근이다. (즉, 총 6개의 근이 있다.)
• 양근은 ${\displaystyle \gamma _{1}}$, ${\displaystyle \gamma _{2}}$, ${\displaystyle \gamma _{1}+\gamma _{2}}$이다. (즉, 총 3개의 양근이 있다.)
• 단순근은 ${\displaystyle \gamma _{1}}$, ${\displaystyle \gamma _{2}}$이다. (즉, 총 2개의 단순근이 있다.)
• 기본 무게는 ${\displaystyle \omega _{1}}$, ${\displaystyle \omega _{2}}$이다. (즉, 총 2개의 기본 무게가 있다.)

다음과 같은 B₂ 근계를 생각하자.

여기서

• 평면의 모든 점은 무게이다. (즉, 그 수는 비가산 무한 개이다.)
• 격자 ${\displaystyle \mathbb {Z} \alpha +\mathbb {Z} \beta /2}$의 원소는 정수 무게이다. (즉, 그 수는 가산 무한 개이다.)
• ${\displaystyle \mathbb {N} (\alpha +\beta )+\mathbb {N} (\alpha +\beta /2)}$의 원소는 우세 정수 무게이다. (즉, 그 수는 가산 무한 개이다.)
• 제1사분면의 점 가운데, y좌표가 x좌표보다 더 큰 점들로 구성된 45° 부채꼴 속의 점은 우세 무게이다. (즉, 그 수는 비가산 무한 개이다.)
• 화살표의 머리들(${\displaystyle \pm \alpha }$, ${\displaystyle \pm \beta }$, ${\displaystyle \pm (\alpha +\beta )}$ ${\displaystyle \pm (2\alpha +\beta )}$)은 근이다. (즉, 총 8개의 근이 있다.)
• 양근은 ${\displaystyle \alpha }$, ${\displaystyle \beta }$, ${\displaystyle \alpha +\beta }$, ${\displaystyle 2\alpha +\beta }$이다. (즉, 총 4개의 양근이 있다.)
• 단순근은 ${\displaystyle \alpha }$, ${\displaystyle \beta }$이다. (즉, 총 2개의 단순근이 있다.)
• 기본 무게는 ${\displaystyle \alpha +\beta }$, ${\displaystyle \alpha +\beta /2}$이다. (즉, 총 2개의 기본 무게가 있다.)

같이 보기

• 리 대수의 표현
• 근계

각주

1. Knapp, Anthony W. (2002). 《Lie groups beyond an introduction》. Progress in Mathematics (영어) 140 2판. Boston: Birkhäuser. ISBN 0-8176-4259-5. MR 1920389. Zbl 1075.22501. CS1 관리 - 추가 문구 (링크)

• Fulton, William; Harris, Joe (1991). 《Representation theory: a first course》. Graduate Texts in Mathematics (영어) 129. Springer. doi:10.1007/978-1-4612-0979-9. ISBN 978-3-540-00539-1. ISSN 0072-5285. MR 1153249. Zbl 0744.22001.

외부 링크

• “Weight of a representation of a Lie algebra”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
• Weisstein, Eric Wolfgang. “Lie algebra weight”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• Weisstein, Eric Wolfgang. “Lie algebra root”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• Weisstein, Eric Wolfgang. “Root lattice”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• “Weight (in representation theory)”. 《nLab》 (영어).
• “Root (in representation theory)”. 《nLab》 (영어).