허블-르메트르 법칙

허블의 법칙이라고도 알려진 허블-르메트르 법칙^[1]은 은하가 거리에 비례하는 속도로 지구에서 멀어지고 있다는 물리 우주론의 관측이다. 다른 말로 하자면, 지구에서 멀수록 더 빨리 멀어진다. 은하의 속도는 은하의 적색편이, 즉 은하에 의하여 방출되는 빛이 가시광선 스펙트럼의 적색 끝쪽으로 이동하는 것에 의하여 결정된다.

은하 대신에 떠오르는 빵 덩어리의 건포도를 사용하여 허블의 법칙을 설명하기 위한 비유이다. 건포도가 다른 건포도보다 한 장소에서 두 배 멀리 떨어져 있다면 더 멀리 있는 건포도는 그 장소에서 두 배 더 빨리 멀어질 것이다.

허블-르메트르의 법칙은 우주팽창에 대한 최초의 관측 근거로 간주되며 오늘날 대폭발(빅뱅) 모형을 뒷받침하는 가장 자주 인용되는 증거 중 하나이다.^[2][3] 이러한 팽창만으로 천체가 움직이는 현상을 허블 흐름(Hubble flow)이라고 한다.^[4] 이는 방정식 v = H₀D 로 기술되는데, 여기서 H₀는, 은하까지의 "고유거리"(proper distance)인 D (이는 공변거리와 달리 시간이 지남에 따라 변할 수 있다)와 분리 속도 v, 즉 우주론적 시간 좌표(cosmological time coordinate)에 대한-아래첨자 0은 오늘날 우주론적 시간의 값을 가리킴- 고유거리의 미분 값("속도"에 대한 이러한 정의의 미묘함에 대한 논의는 "고유거리의 사용"을 참조) 사이의 비례 상수인 허블 상수(Hubble constant)이다.

허블 상수는 가장 자주 (km/s)/Mpc의 단위로 인용되고, 따라서 1메가파섹(3.09 × 10¹⁹ km) 떨어진 은하의 속도를 km/s 단위로 나타내는데, 그 값-근래 측정치-은 약 70(km/s)/Mpc이다. 그런데 H₀의 SI 단위는 단순히 s^-1 이고 H₀의 역수에 대한 SI 단위는 단순히 초이다. H₀의 역수는 허블 시간(Hubble time)으로 알려져 있다. 허블 상수는 팽창의 상대 속도로 해석될 수도 있다. 이 형식에서 H₀ = 7%/Gyr는 현재 팽창 속도에서 비속박(unbound) 구조가 7% 성장하는 데 10억 년이 걸리는 것을 의미한다.

에드윈 허블에 의해 널리 알려졌지만,^[5][6][7] 우주가 계산 가능한 속도로 팽창한다는 개념은 1922년 알렉산더 프리드만에 의해 일반 상대성이론 방정식에서 처음으로 도출되었다. 프리드만은 현재 프리드만 방정식으로 알려진 일련의 방정식을 발표했는데, 이 방정식은 우주가 팽창하고 있는 것 같음을 보여주고, 그러할 경우에서의 팽창 속도를 보여준다.^[8] 그런 다음 1927년 소논문에서 조르주 르메트르는 독립적으로 우주가 팽창하는 것 같다는 것을 도출했고, 멀리 떨어진 물체의 후퇴 속도와 거리 사이의 비례를 관찰하고 비례 상수의 추정값을 제안했는데; 이 상수는 에드윈 허블이 우주 팽창의 존재를 확인하고 2년 후 더 정확한 값을 결정했을 때 허블 상수라는 이름으로 알려지게 되었다.^{[2][9][10][11][12]} 허블은 적색편이로부터 물체의 후퇴 속도를 추론했는데, 그 중 많은 것들이 1917년 베스토 슬라이퍼에 의해 속도와 관련되어 더 일찍 측정되었다.^[13][14][15] 허블 상수 H₀는 주어진 순간에 속도-거리 공간에서는 개략 일정하지만, 허블 상수가 현재 값인 허블 매개변수 H가 시간에 따라 변하기 때문에 상수라는 용어는 때때로 잘못된 이름(misnomer)으로 여겨진다.^[16][17]

발견

허블 상수로 가는 3단계^[18]

허블이 그의 관측을 하기 10년 전, 많은 물리학자와 수학자들은 일반 상대성 이론의 아인슈타인 방정식을 사용하여 팽창하는 우주에 대한 일관된 이론을 확립했다. 가장 일반적인 원리를 우주의 본질(nature)에 적용하기는 당시 우세했던 정적 우주 개념과 충돌하는 동역학적 해를 산출하였다.

슬리퍼의 관찰

1912년 베스토 슬라이퍼는 "나선형 성운"(나선은하의 구식 용어)의 첫 번째 도플러 효과를 측정했으며 곧 거의 모든 그러한 성운이 지구에서 멀어지고 있음을 발견했다. 그는 이 사실의 우주론적 의미를 이해하지 못했으며, 실제로 당시에는 이 성운이 우리 은하수 밖에 있는 "섬 우주"인지 여부에 대하여 대논쟁이 있었다.^[19][20]

FLRW 방정식

1922년 알렉산더 프리드만은 아인슈타인 방정식에서 그의 프리드만 방정식을 유도하여 우주가 방정식으로 계산할 수 있는 속도로 팽창하는 것 같음을 보여주었다.^[21] 프리드만이 사용하는 매개변수는 오늘날 척도인자로 알려져 있으며 허블 법칙의 비례 상수의 척도 불변 형태로 간주될 수 있다. 조르주 르메트르는 다음 단락에서 논의된 1927년 논문에서 유사한 해를 독립적으로 찾았다. 프리드만 방정식은 균질한 등방성 우주에 대한 계량을 주어진 밀도와 압력을 갖는 유체에 대한 아인슈타인의 장 방정식에 삽입하여 도출된다. 팽창하는 시공간에 대한 이러한 아이디어는 결국 우주론의 대폭발(빅뱅) 및 정상우주론으로 이어지게 되었다.

르메트르의 방정식

허블이 자신의 논문을 발표하기 2년 전인 1927년, 벨기에의 성직자이자 천문학자인 조르주 르메트르는 현재 허블의 법칙으로 알려진 것을 도출한 연구를 최초로 발표했다. 캐나다 천문학자 시드니 반 덴 버그_{Sidney van den Bergh}에 따르면 "1927년 르메트르에 의한 우주 팽창의 발견은 영향력이 적은 저널에 프랑스어로 출판되었다. 이 기사의 1931년 영향력 있는 영어 번역에서 결정적인 방정식이 현재 허블 상수로 알려진 것에 대한 참조를 생략함으로써 변경되었다."^[22] 번역된 논문의 변경은 르메트르 자신이 수행한 것으로 현재 알려져 있다.^[10][23]

우주의 모양

현대 우주론이 등장하기 전에는 우주의 모양와 크기에 대해서 상당한 논의가 있었다. 1920년, 할로우 섀플리와 히버 다우스트 커티스 사이에 이 문제에 대해 섀플리-커티스 논쟁이 일어났다. 섀플리는 우리 은하 크기의 작은 우주를 주장했고, 커티스는 우주가 훨씬 더 크다고 주장했다. 이 문제는 허블의 개선된 관측으로 향후 10년 안에 해결되었다.

우리은하 밖의 세페이드 변광성

에드윈 허블은 당시 세계에서 가장 강력한 망원경이 있던 윌슨산 천문대^[24]에서 전문적인 천문 관측 작업의 대부분을 수행했다. 그는 1920년대에 "나선 성운" 속에 있는 세페이드 변광성 하나를 이용하여 이 은하의 거리를 측정했다. (그는 이 별의 변광 주기를 측정하고 이 별 밝기의 절대등급을 확인함으로써 거리를 계산할 수 있었다. 세페이드 변광성 덕분에 천문학자들은 최초로 거리의 척도를 마련하여 이를 은하에도 적용할 수 있게 되었다. 나중에 허블과 다른 천문학자들이 은하의 거리를 측정하는 다른 방법들을 개발했지만 지금도 여전히 세페이드 변광성 기법은 모든 사람들로부터 신뢰를 받고 있다.) 놀랍게도, 이 물체는 은하수 바깥쪽에 위치한 거리에 있는 것으로 밝혀졌다. 그것들은 계속해서 '성운'으로 불리었고, '은하'라는 용어가 그것을 단지 점진적으로 대체하였다.

적색편이와 거리 측정의 결합

허블의 법칙에 대한 적색편이 속도의 적합성.^[25] 허블 상수에 대한 다양한 추정치가 존재한다. 허블망원경(HST) Key H₀ 그룹은 H₀ = 71 ± 2(통계적) ± 6(체계적) km s⁻¹Mpc⁻¹,^[26]을 발견하기 위해 0.01과 0.1 사이의 적색편이에 대해 유형 Ia 초신성을 적용한 반면에, 샌디지_Sandage 등은 H₀ = 62.3 ± 1.3(통계적) ± 5(체계적) km s⁻¹Mpc⁻¹을 발견한다.^[27]

허블의 법칙, 속도, 거리에 나타나는 변수들은 직접적으로 측정되는 것이 아니다. 실제로 우리가, 말하자면, 한 초신성 밝기를 결정하면, 이 밝기가 그 거리와 복사 스펙트럼의 적색편이 z = ∆λ/λ에 대한 정보를 제공한다. 허블은 밝기와 변수 z를 상호연관시켰다.

허블은 그의 은하 거리 측정값을 베스토 슬라이퍼와 밀턴 휴메이슨의 은하계와 관련된 적색편이 측정값과 결합하여 물체의 적색편이와 그 거리 사이의 대략적인 비례성을 발견했다. 상당한 분산(scattering)이 있었지만(지금은 특이속도로 인해 발생하는 것으로 알려져 있음-'허블 흐름'은 후퇴 속도가 국부적인 고유 속도보다 더 클 정도로 충분히 멀리 떨어진 공간 영역을 나타내는 데 사용됨), 허블은 그가 연구한 46개 은하의 추세선(trend line)을 분석하여 500 km/s/Mpc의 허블 상수 값을 얻는다(그의 거리 보정 오류로 인해 현재 허용되는 값보다 훨씬 높음; 자세한 내용은 우주 거리 사다리 참조).

허블의 법칙이 발견되고 발전될 당시에는 적색편이 현상을 특수 상대성이론의 맥락에서 도플러 편이로 설명하고, 적색편이 z 와 속도를 연관시키기 위해 도플러 공식을 사용하는 것이 용인되었다. 오늘날에는 일반 상대성이론의 맥락에서 먼 물체 사이의 속도는 사용되는 좌표의 선택에 따라 달라지므로 적색 편이는 도플러 효과 또는 팽창하는 공간으로 인한 우주론적 이동(cosmological shift)(또는 중력적)이거나 또는 둘의 어떤 조합으로 똑같이 기술될 수 있다.^[28]

허블 다이어그램

허블의 법칙은 물체의 속도(적색편이에 대략적으로 비례한다고 가정)가 관찰자로부터의 거리에 대해 표시되는 "허블 다이어그램"으로 쉽게 묘사될 수 있다.^[29] 이 다이어그램에서 양의 기울기의 직선은 허블의 법칙을 시각적인 묘사이다.

버려진 우주상수

 이 부분의 본문은 우주상수입니다.

허블의 발견이 발표된 후 알베르트 아인슈타인은 일반 상대성 이론을 수정하여 우주의 올바른 상태라고 생각한 정적 해를 생성하도록 설계한 우주상수에 대한 작업을 포기했다. 가장 단순한 형태 모형인 아인슈타인 방정식은 팽창하거나 수축하는 우주를 생성하므로 완벽한 정적 및 평평한 우주를 얻기 위해 팽창 또는 수축에 대응하기 위해 아인슈타인의 우주상수가 인위적으로 생성되었다.^[30] 우주가 실제로 팽창하고 있다는 허블의 발견 이후, 아인슈타인은 우주가 정지되어 있다는 잘못된 가정을 자신의 "가장 큰 실수"라고 불렀다.^[30] 일반 상대성 이론은, 자체적으로도, 우주의 팽창을 예측할 수 있었고, 그것은 (거대한 질량에 의한 빛의 휘어짐이나 수성 궤도의 세차 운동과 같은 관측을 통해) 실험적으로 관찰될 수 있었고 또한 그가 원래 공식화했던 방정식의 특정 해를 사용한 그의 이론적 계산과 비교될 수 있었다.

1931년에 아인슈타인은 현대 우주론의 관측 기반을 제공한 허블에 감사하기 위해서 윌슨 산 천문대를 방문했다.^[31]

우주상수는 최근 수십 년 동안 암흑 에너지에 대한 가설로 다시 주목을 받고 있다.^[32]

해석

단순 선형 관계 v = cz를 포함하여 가능한 다양한 후퇴 속도 대 적색편이 함수 '; 일반 상대성 이론과 관련된 이론으로부터 가능한 다양한 형태; 특수 상대성 이론에 따라 빛보다 빠른 속도를 허용하지 않는 곡선. 모든 곡선은 낮은 적색 편이에서 선형이다. 데이비스_Davis와 라인위버_Lineweaver를 참조하라.

적색편이와 거리 사이의 선형 관계에 대한 발견은 후퇴 속도(recessional velocity)와 적색편이 사이의 선형 관계에 대한 가정과 결합되어 허블의 법칙에 대한 간단한 수학적 표현을 다음과 같이 제시한다:

${\displaystyle v=H_{0}\,D}$

여기서

• ${\displaystyle v}$는 일반적으로 km/s 로 표시되는 후퇴 속도이다.
• H₀는 허블 상수이며 다음 값에 해당한다.

시간 아래첨자 0으로 표시된 관찰 시점(보통 오늘날을 가리킴)에 취한 프리드만 방정식에서 H(종종 시간 종속적인 값이고 척도인자로 표현될 수 있는 값인 허블 매개변수라고도 함). 이 값은 주어진 한 공변시간에 우주 전체에서 동일하다.

• ${\displaystyle D}$는 주어진 우주시에 의해 정의된 3차원 공간에서 메가파섹(Mpc)으로 측정되는 은하에서 관찰자까지의 고유거리(공변거리와 달리 시간이 지남에 따라 변할 수 있음)이다. (후퇴 속도는 바로 v = dD/dt).

허블-르메트르의 법칙은 후퇴 속도와 거리 사이의 근본적인 관계로 간주된다. 그러나 후퇴 속도와 적색편이 사이의 관계는 채택된 우주론적 모형에 따라 달라지며 작은 적색편이를 제외하고는 확립되지 않았다.

거리 D가 허블 구(Hubble sphere) r_HS의 반경보다 큰 경우 물체는 광속보다 빠른 비례로 후퇴한다(이의 중요성에 대한 논의는 고유거리의 사용 참조):

${\displaystyle r_{HS}={\frac {c}{H_{0}}}\ .}$

허블 "상수"는 시간이 아닌 공간에서만 상수이기 때문에 허블 구의 반경은 다양한 시간 간격에 따라 증가하거나 감소할 수 있다. 아래첨자 0은 그중 오늘의 허블 상수 값을 나타낸다.^[33] 현재의 증거는 우주의 팽창이 가속되고 있음을 시사하며(우주의 가속 팽창 참조), 이는 주어진 은하에 대해 은하가 점점 더 먼 거리로 이동함에 따라 후퇴 속도 dD/dt가 시간이 지남에 따라 증가한다는 것을 의미한다. 그러나 허블 매개변수는 실제로 시간이 지남에 따라 감소하는 것으로 생각된다. 즉, 고정된 거리 D를 보고 일련의 서로 다른 은하가 그 거리를 통과하는 것을 지켜본다면 이후의 은하들은 이전 은하보다 더 느린 속도로 그 거리를 통과할 것이다.^[34]

적색편이 속도와 후퇴 속도

적색편이는 먼 퀘이사에 대한 수소 α선과 같은 알려진 전이의 파장을 결정하고 고정 기준과 비교된 부분 이동을 찾음으로써 측정할 수 있다. 따라서 적색편이는 실험적 관찰에 있어 모호하지 않은 양이다. 적색편이와 후퇴 속도의 관계는 또 다른 문제이다. 광범위한 토론은 해리슨_Harrison을 참조하라.^[35]

적색편이 속도

적색편이 z는 종종 '적색편이 속도'로 설명되며, 이는 '만일' 선형 도플러 효과에 의해 유발되면 동일한 적색편이를 생성하는 후퇴 속도이다(그러나 편이가 부분적으로 공간의 우주론적 팽창과 관련된 경우는 그렇지 않은데, 이는 속도가 너무 커서 도플러 이동에 대한 비상대론적 공식을 사용하기 어렵기 때문이다). 이 적색편이 속도는 빛의 속도를 쉽게 초과할 수 있다.^[36] 다시 말해, 적색편이 속도 v_rs를 결정하기 위해서 관계:

${\displaystyle v_{rs}\equiv cz,}$ 가

사용된다.^[37][38] 즉, 적색편이 속도와 적색편이 사이에는 '근본적인 차이가 없음'이니: 즉, 적색편이 속도는 엄격하게 비례하며 어떠한 이론적 추론과도 관련이 없다. "적색편이 속도"라는 용어의 배경은 적색편이 속도가 소위 피조-도플러 공식(Fizeau-Doppler formula)의 낮은 속도의 단순화로부터의 속도와 일치하기 때문이다.^[39]

${\displaystyle z={\frac {\lambda _{o}}{\lambda _{e}}}-1={\sqrt {\frac {1+{\frac {v}{c}}}{1-{\frac {v}{c}}}}}-1\approx {\frac {v}{c}}.}$

여기서 λ_o, λ_e는 각각 관측 파장과 방출 파장이다. 그러나 "적색편이 속도" v_rs는 더 큰 속도에서의 실제 속도와 그렇게 단순하게 관련되지 않으며, 이 용어가 실제 속도로 해석되는 경우에는 혼동을 야기한다. 다음으로 적색편이 또는 적색편이 속도와 후퇴 속도 사이의 관계에 대해 논의한다. 이 논의는 사르토리_Sartori를 기반으로 한다.^[40]

후퇴 속도

R(t)가 우주의 척도인자라고 하고 선택된 우주론적 모형에 의존하는 방식으로 우주가 팽창함에 따라 증가한다고 가정하라. 그 의미는 공변하는 점 사이에서 측정된 모든 고유거리 D(t)는 R에 비례하여 증가한다는 것이다. (공변하는 점들은 공간의 확장에 의한 결과 외에는 서로 상대적으로 움직이지 않는다.) 바꾸어 말하면:

${\displaystyle {\frac {D(t)}{D(t_{0})}}={\frac {R(t)}{R(t_{0})}},}$^[41]

여기서 t₀은 어떤 기준 시간이다. 빛이 시간 t_e에서 은하에서 방출되고 t₀에서 우리에 의해 관측되면 공간 확장으로 인해 적색편이가 되며 이 적색편이 z는 간단히:

${\displaystyle z={\frac {R(t_{0})}{R(t_{e})}}-1.}$

은하가 거리 D에 있고 이 거리는 d_tD의 비율로 시간에 따라 변한다고 가정하라. 우리는 이 후퇴의 비율을 "후퇴 속도" v_r이라고 부른다:

${\displaystyle v_{r}=d_{t}D={\frac {d_{t}R}{R}}D.}$

이제 허블 상수를 다음과 같이 정의하여

${\displaystyle H\equiv {\frac {d_{t}R}{R}},}$

그리고 허블-르메트르 법칙을 발견한다:

${\displaystyle v_{r}=HD.}$

이러한 관점에서 허블-르메트르 법칙은 (i) 우주의 팽창에 의한 후퇴 속도와 (ii) 물체까지의 거리 사이의 근본적인 관계이다. 적색편이와 거리 사이의 연결은 허블-르메트르 법칙과 관측을 연결하는 데 사용되는 한 버팀목(crutch)이다. 이 법칙은 테일러 급수 확장을 통해 대략적으로 적색편이 z와 연관 시킬 수 있다:

${\displaystyle z={\frac {R(t_{0})}{R(t_{e})}}-1\approx {\frac {R(t_{0})}{R(t_{0})\left(1+(t_{e}-t_{0})H(t_{0})\right)}}-1\approx (t_{0}-t_{e})H(t_{0}),}$

거리가 너무 크지 않으면 모형의 다른 모든 복잡성은 작은 보정이 되며, 시간 간격은 단순히 거리를 빛의 속도로 나눈 것이다:

${\displaystyle z\approx (t_{0}-t_{e})H(t_{0})\approx {\frac {D}{c}}H(t_{0}),}$

또는

${\displaystyle cz\approx DH(t_{0})=v_{r}.}$

이 접근법에 따르면 관계 cz = v_r 은 낮은 적색편이에서 유효한 근사치이며, 모형-의존적인 큰 적색편이에서의 관계로 대체된다. 앞의 속도-적색편이 그림을 참조하라.

매개변수의 관찰 가능성

엄밀히 말해서 공식에서 v와 D는 모두 직접 관측할 수 없다. 왜냐하면 그것들은 현재 은하의 속성이기 때문이다. 반면에 우리의 관측은 우리가 현재 보고 있는 빛이 떠난 당시의 과거 은하를 나타낸다.

상대적으로 가까운 은하의 경우(적색편이 z가 1보다 훨씬 작음) v와 D는 크게 변하지 않을 것이며 v는 ${\displaystyle v=zc}$ (여기서 c는 빛의 속도) 공식을 사용하여 추정할 수 있다. 이것은 허블이 발견한 경험적 관계를 제공한다.

멀리 떨어진 은하의 경우에는 시간에 따라 H가 어떻게 변하는지에 대한 상세한 모형을 지정하지 않고는 z에서 v(또는 D)를 계산할 수 없다. 적색편이는 빛이 방출할 때의 후퇴 속도와 직접적인 관련이 없지만 간단한 해석이 있으니: (1+z)는 광자가 관찰자를 향해 이동하는 동안 우주가 팽창한 요인이다.

팽창속도 대 상대속도

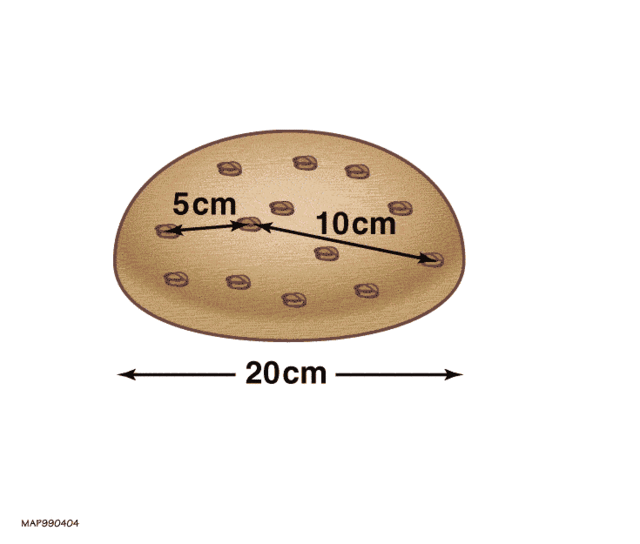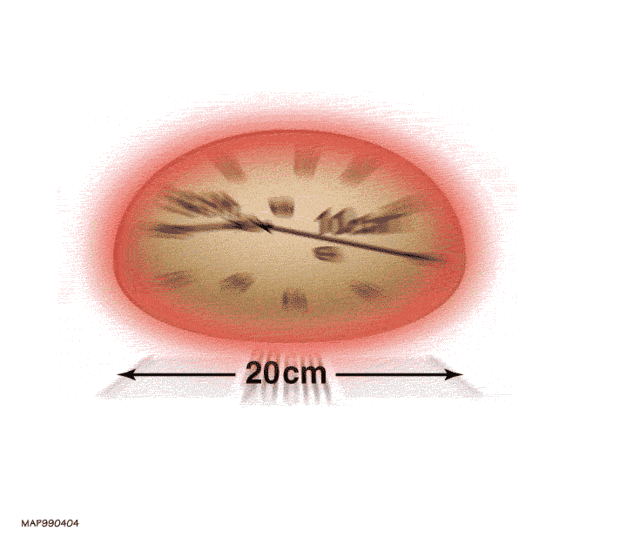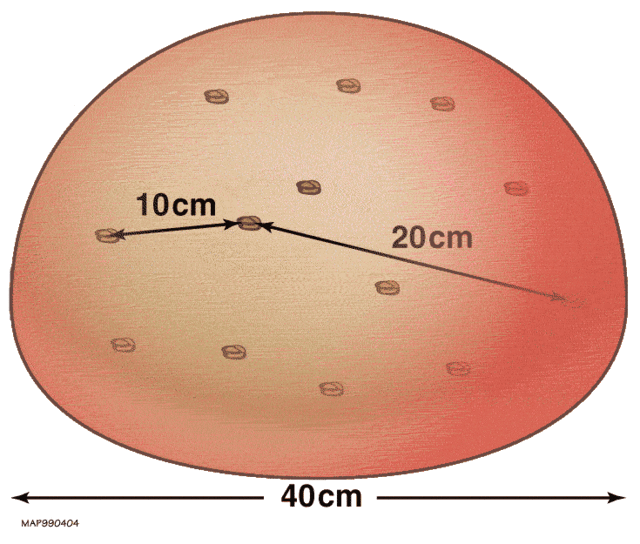
거리를 결정하기 위해 허블의 법칙을 사용할 때 우주의 팽창으로 인한 속도만 사용할 수 있다. 중력적으로 상호작용하는 은하는 우주의 팽창과 무관하게 서로에 대해 상대적으로 움직이기 때문에^[42] 특이속도라고 불리는 이러한 상대속도는 허블의 법칙을 적용할 때 고려되어야 한다.

신의 손가락(Finger of God) 효과는 이 현상의 한 결과이다. 은하계나 행성계와 같이 중력적으로 구속된 시스템에서는 공간의 팽창은 중력의 인력보다 훨씬 약한 효과이다.

허블 매개변수의 시간 의존성

매개변수 ${\displaystyle H}$는 일반적으로 "허블 상수"라고 하지만 고정된 시간에만 공간에서 일정하기 때문에 잘못된 이름이다. 그것은 거의 모든 우주론적 모형에서 시간에 따라 변하며, 멀리 떨어진 물체에 대한 모든 관찰은 "상수"가 다른 값을 가졌던 먼 과거에 대한 관찰이기도 하다. 오늘날 값을 나타내는 ${\displaystyle H_{0}}$와 더불어 "허블 매개변수"가 더 정확한 용어이다.

혼란의 또 다른 일반적인 원인은 가속 팽창하는 우주는 허블 매개변수가 실제로 시간이 지남에 따라 증가한다는 것을 의미하지 않는다는 것이니; 왜냐하면 ${\displaystyle H(t)\equiv {\dot {a}}(t)/a(t)}$ 이고, 대부분의 가속 모형에서는 ${\displaystyle a}$는 ${\displaystyle {\dot {a}}}$ 보다 상대적으로 빠르게 증가하기 때문에, 따라서 H는 시간이 지남에 따라 감소한다. (선택된 한 은하의 후퇴 속도는 증가하지만, 고정된 반지름을 가진 구를 통과하는 다른 은하는 나중에 구를 더 느리게 통과한다.)

무차원 감속 매개변수를 정의하는 데에는

${\displaystyle q\equiv -{\frac {{\ddot {a}}\,a}{{\dot {a}}^{2}}}}$, 그것은 다음으로 되어

${\displaystyle {\frac {dH}{dt}}=-H^{2}(1+q).}$

이것으로부터 ${\displaystyle q<-1}$ 가 아니면 허블 매개변수는 시간이 지남에 따라 감소한다는 것을 알 수 있으며; 그것은 우주가 팬텀 에너지(phantom energy)를 포함하는 경우에만 발생할 수 있으며, 이론적으로 다소 있을 수 없는 것으로 간주된다.

그러나, 표준 ΛCDM 모형에서 우주상수가 물질에 대해 점점 더 우세해짐에 따라 먼 미래에 ${\displaystyle q}$는 위에서 -1이 되는 경향이 있으며; 이것은 ${\displaystyle H}$가 위로부터 ${\displaystyle \approx 57}$ km/s/Mpc의 일정한 값에 접근할 것이고, 또한 우주의 척도인자가 그래서 시간에 따라 지수적으로 증가할 것을 의미한다.

이상화된 허블의 법칙

균일하게 팽창하는 우주에 대한 이상화된 허블 법칙의 수학적 유도는 3차원 데카르트 좌표계/뉴턴 좌표 공간에서 기하학의 상당히 기본적인 정리이며, 그것은 거리 공간으로 간주되며 완전히 균질하고 등방성이다 (속성은 위치나 방향에 따라 변하지 않는다.). 간단히 말해서 정리는 다음과 같으니:

직선을 따라 원점으로부터의 거리에 비례하는 속도로 원점에서 멀어지는 모든 두 점은 거리에 비례하는 속도로 서로 멀어진다.

사실 이것은 비데카르트 공간이 국지적으로 균질하고 등방성인 한, 특히 우주론적 모형로 자주 고려되는 음과 양으로 구부러진 공간에도 적용된다(우주의 모양을 참조하라).

이 정리에서 비롯된 관찰은 지구에서 물체가 멀어지는 것을 보는 것은 팽창이 일어나는 중심에 지구가 가까이 있다는 표시가 아니라 팽창하는 우주의 "모든" 관찰자가 그것들로부터 멀어지는 물체를 볼 것이라는 것이다.

우주의 궁극적 운명과 나이

우주의 나이와 우주의 종말은 오늘날 허블 상수를 측정하고 밀도 매개 변수(물질을 위해서 (Ω_M 또한 암흑 에너지를 위해서는 Ω_Λ)로 고유하게 특징지어지는 감속 매개변수의 관측값으로 추론하여 결정할 수 있다. Ω_M > 1 및 Ω_Λ = 0과 함께 하는 "닫힌 우주"는 대함몰에서 끝나며 허블 나이보다 상당히 젊다. Ω_M ≤ 1 및 Ω_Λ = 0과 함께 하는 "열린 우주"는 영원히 팽창하며 허블 나이에 가까운 나이를 가지고 있다. 우리가 살고 있는 0 아닌 Ω_Λ과 함께 하는 가속 우주의 나이는 공교롭게도 허블 시대에 매우 가깝다.

허블 매개변수의 값은 시간이 지남에 따라 변경되는데, 소위 감속 매개변수(deceleration parameter)의 다음에 의해 정의된 q 값에 따라 증가하거나 감소하니

${\displaystyle q=-\left(1+{\frac {\dot {H}}{H^{2}}}\right).}$

감속 매개변수가 0인 우주에서는 H = 1/t이며, 여기서 t는 대폭발(빅뱅) 이후 시간dl다. 0이 아닌 시간 의존적인 ${\displaystyle q}$ 값은 단순히 현재로부터 입자 지평선 크기가 0이었던 시점까지 프리드만 방정식의 적분을 필요로 한다.

중력에 의해 팽창이 느려지고 있음을 나타내는 q는 양수라고 오랫동안 생각되어 왔다. 이것은 우주의 나이가 1/H(그것은 약 140억 년) 미만임을 의미한다. 예를 들어, 1/2(한때 대부분의 이론가들이 선호했던)인 q값은 우주의 나이를 2/(3H)로 나타낸다. 1998년 q가 분명히 음수라는 발견은 우주가 실제로 1/H 보다 더 오래되었을 수 있음을 의미한다. 그러나 우주의 나이 추정치는 1/H에 매우 가깝다.

올베르스의 역설

 이 부분의 본문은 올베르스의 역설입니다.

허블-르메트르 법칙의 대폭발(빅뱅) 해석으로 요약된 우주의 팽창은 올베르스의 역설로 알려진 오래된 수수께끼와 관련이 있다. 만약 우주가 무한하고, 정적이고, 별들의 균일한 분포로 가득 차 있다면, 하늘의 모든 시선은 한 별 위에서 끝날 것이고, 하늘은 한 별의 표면만큼 밝을 것이다. 하지만 밤하늘은 대체로 어둡다.^[43][44]

17세기 이래로 천문학자들과 다른 사상가들은 이 역설을 해결할 수 있는 여러 가지 가능한 방법을 제안했지만 현재 받아들여지는 해결 방법은 부분적으로는 대폭발(빅뱅) 이론에, 부분적으로는 허블 확장에 달려 있으니: 유한한 양의 시간으로 존재하는 우주에서는 유한한 별들의 빛만이 우리에게 도달할 수 있는 충분한 시간을 가지므로 그래서 역설이 해결된다. 게다가 팽창하는 우주에서는 멀리 있는 물체는 우리가 볼 때 시간에 따라 물체에서 방출되는 빛이 적색 편이되고 또한 밝기가 감소하면서 멀어진다.^[43][44]

무차원 허블 상수

허블 상수로 작업하는 대신에 보통 h로 표시되고 일반적으로 "작은 h"^[45]라고 하는 무차원 허블 상수를 도입한 다음 허블 상수 H₀를 h = 100 km s⁻¹ Mpc 로 작성하는 것이 일반적 실행이며, H₀의 참 값의 모든 상대 불확실성은 h로 위임된다.^[46] 무차원 허블 상수는 공식 d ≈ c/H₀ × z를 사용하여 적색편이 z에서 계산된 거리를 제공할 때 자주 사용된다. H₀가 정확히 알려져 있지 않기 때문에 그 거리는 표현되기를:

${\displaystyle cz/H_{0}\approx (2998\times z){\text{ Mpc }}h^{-1}.}$

다른 말로는, 2998 × z를 계산하고 단위를 ${\displaystyle {\text{Mpc }}h^{-1}}$ 또는 ${\displaystyle h^{-1}{\text{ Mpc}}}$ 로 부여한다.

때때로 100 이외의 참조 값이 선택될 수 있으며, 이 경우 혼동을 피하기 위해 h뒤에 아래첨자가 표시된다. 예를 들어 h₇₀ 은 ${\displaystyle h/0.7}$를 의미하는${\displaystyle H_{0}=70\,\mathrm {km\,s^{-1}\,Mpc^{-1}} }$를 나타낸다.

이것은 일반적으로 H₀에 1.75 × 10⁻⁶³ (파섹 및 t_P의 정의에서)를 곱하여 얻은 플랑크 단위로 표시되는 허블 상수의 무차원 값과 혼동되어서는 안 되며, 예를 들어 H₀ = 70를 위해서는 1.2 × 10⁻⁶¹의 플랑크 단위 버전을 얻는다.

팽창의 가속화

 이 부분의 본문은 우주의 가속 팽창입니다.

1998년에 음수로 결정된 Ia형 초신성의 표준 촉광(standard candles) 관측에서 측정된 q의 값은 우주의 팽창이 현재 "가속"한다는 암시로서 많은 천문학자들을 놀라게 했다^[47] (하지만 앞에서 해석 섹션에서 언급했듯이 허블 계수는 여전히 시간이 지남에 따라 여전히 감소하고 있음; 암흑 에너지 및 ΛCDM 모형에 대한 항(article) 참조).

허블 매개변수의 유도

프리드만 방정식으로부터 (약간 변형해서) 시작하면:

${\displaystyle H^{2}\equiv \left({\frac {\dot {a}}{a}}\right)^{2}={\frac {8\pi G}{3}}\rho -{\frac {kc^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}},}$

여기서 ${\displaystyle H}$는 허블 매개변수, ${\displaystyle a}$는 척도인자, G는 중력 상수, ${\displaystyle k}$는 우주의 정규화된 공간 곡률이며 -1, 0 또는 1과 같고 또한 ${\displaystyle \Lambda }$는 우주 상수이다.

물질-지배 우주 (우주 상수 포함)

우주가 물질-지배라면 우주 ${\displaystyle \rho }$의 질량 밀도는 단지 물질을 포함하는 것으로 간주할 수 있으므로

${\displaystyle \rho =\rho _{m}(a)={\frac {\rho _{m_{0}}}{a^{3}}},}$

여기서 ${\displaystyle \rho _{m_{0}}}$는 오늘날 물질의 밀도이다. 프리드만 방정식과 열역학 원리로부터 우리는 질량 밀도가 우주의 부피에 역비례하여 감소한다는 비상대론적 입자에 대해 알고 있으므로 위의 방정식이 참이어야 한다. 우리는 정의할 수도 있다(${\displaystyle \Omega _{m}}$ 에 대한 밀도 매개변수 참조).

${\displaystyle \rho _{c}={\frac {3H_{0}^{2}}{8\pi G}};}$

${\displaystyle \Omega _{m}\equiv {\frac {\rho _{m_{0}}}{\rho _{c}}}={\frac {8\pi G}{3H_{0}^{2}}}\rho _{m_{0}};}$

그러므로

${\displaystyle \rho ={\frac {\rho _{c}\Omega _{m}}{a^{3}}}.}$

또한 정의에 따라서,

${\displaystyle \Omega _{k}\equiv {\frac {-kc^{2}}{(a_{0}H_{0})^{2}}}}$

${\displaystyle \Omega _{\Lambda }\equiv {\frac {\Lambda c^{2}}{3H_{0}^{2}}},}$

여기서 아래첨자 0은 오늘의 값을 나타내고 ${\displaystyle a_{0}=1}$이다. 이 모든 것을 이 항 시작의 프리드만 방정식에 대입하고 ${\displaystyle a}$를 ${\displaystyle a=1/(1+z)}$ 로 바꾸면 주기를

${\displaystyle H^{2}(z)=H_{0}^{2}\left(\Omega _{m}(1+z)^{3}+\Omega _{k}(1+z)^{2}+\Omega _{\Lambda }\right).}$

물질-지배 및 암흑 에너지-지배 우주

우주가 물질-지배하고 암흑 에너지-지배 둘 다라면, 위의 허블 매개변수 방정식은 암흑 에너지 상태 방정식의 함수이기도 하다. 그래서 지금은:

${\displaystyle \rho =\rho _{m}(a)+\rho _{de}(a),}$

여기서 ${\displaystyle \rho _{de}}$는 암흑 에너지의 질량 밀도이다. 정의에 따르면, 우주론의 상태 방정식은 ${\displaystyle P=w\rho c^{2}}$이며, 이것을 유체 방정식에 대입하면 우주의 질량 밀도가 시간에 따라 어떻게 진화하는지 기술하는데, 그러면

${\displaystyle {\dot {\rho }}+3{\frac {\dot {a}}{a}}\left(\rho +{\frac {P}{c^{2}}}\right)=0;}$

${\displaystyle {\frac {d\rho }{\rho }}=-3{\frac {da}{a}}(1+w).}$

만일 w 가 상수라면,

${\displaystyle \ln {\rho }=-3(1+w)\ln {a};}$

의미하기를:

${\displaystyle \rho =a^{-3(1+w)}.}$

따라서 상태 w의 상수 방정식을 갖는 암흑 에너지의 경우 ${\displaystyle \rho _{de}(a)=\rho _{de0}a^{-3(1+w)}}$이다. 이것을 이전과 유사한 방식으로 프리드만 방정식에 대입하되, 이번에는 공간적으로 평평한 우주를 가정하는 ${\displaystyle k=0}$ 을 설정하면 (우주의 모양 참조)

${\displaystyle H^{2}(z)=H_{0}^{2}\left(\Omega _{m}(1+z)^{3}+\Omega _{de}(1+z)^{3(1+w)}\right).}$

암흑 에너지가 아인슈타인이 도입한 것과 같은 우주상수에서 파생된 경우 ${\displaystyle w=-1}$ 로 표시할 수 있다. 그런 다음 방정식은 ${\displaystyle \Omega _{k}}$ 가 0으로 설정된 앞의 물질-지배 우주 항의 마지막 방정식으로 축소된다. 이 경우 초기 암흑 에너지 밀도 ${\displaystyle \rho _{de0}}$는 주어지기를^[48]

${\displaystyle \rho _{de0}={\frac {\Lambda c^{2}}{8\pi G}}}$ and ${\displaystyle \Omega _{de}=\Omega _{\Lambda }.}$

이를 해결하려면 ${\displaystyle w(a)}$를 매개변수화해야 한다. 예를 들어 ${\displaystyle w(a)=w_{0}+w_{a}(1-a)}$ 인 경우에는, 주기를

${\displaystyle H^{2}(z)=H_{0}^{2}\left(\Omega _{m}a^{-3}+\Omega _{de}a^{-3\left(1+w_{0}+w_{a}\right)}e^{3w_{a}a}\right).}$^[49]

다른 성분들은 최근에 공식화되었다.^[50][51][52]

허블 상수에서 파생된 단위들

허블 시간

허블 상수 ${\displaystyle H_{0}}$에는 역시간 단위가 있으니; 허블 시간 t_H는 단순히 허블 상수의 역수로 정의되어,^[53] 즉

${\displaystyle t_{H}\equiv {\frac {1}{H_{0}}}={\frac {1}{67.8{\textrm {(km/s)/Mpc}}}}=4.55\times 10^{17}s=14.4{\text{ billion years}}.}$

이것은 우주의 나이가 약 138억 년인 것과는 약간 다르다. 허블 시간은 팽창이 선형이었다면 가졌을 나이로, 팽창이 선형이 아니기 때문에 우주의 실제 나이와 다르니; 그것들은 표준 ΛCDM 모형에서 약 0.96인 우주의 질량-에너지 함량에 의존하는 무차원 요인에 의해 관련된다.

우리는 현재 진공 에너지(vacuum energy)의 지배력 증가로 인해 우주의 팽창이 지수적으로 증가하는 시기에 접근하고 있는 것으로 보인다. 이 체제에서 허블 매개변수는 일정하고 우주는 각 허블 시간마다 계수 e 만큼 성장한다:

${\displaystyle H\equiv {\frac {\dot {a}}{a}}={\textrm {constant}}\quad \Longrightarrow \quad a\propto e^{Ht}=e^{\frac {t}{t_{H}}}}$

마찬가지로, 일반적으로 허용되는 값 2.27 Es⁻¹ 은 (현재 속도에서) 우주가 엑사(10¹⁸-백경)초당 ${\displaystyle e^{2.27}}$ 배로 성장할 것이라는 것을 의미한다.

오랜 시간 동안에 걸쳐서, 그 역학은 위에서 설명한 일반 상대성 이론, 암흑 에너지, 급팽창 이론 등에 의해서 복잡해진다.

허블 길이

허블 길이 또는 허블 거리는 ${\displaystyle cH_{0}^{-1}}$ 로 정의되는 우주론의 거리 단위로, 빛의 속도에 허블 시간을 곱한 값이다. 44억 2000만 파섹 또는 144억 광년에 해당한다. (광년 단위의 허블 길이의 숫자 값은 정의상 허블 시간의 연도와 같다.) 허블 거리는 ${\displaystyle D=cH_{0}^{-1}}$를 허블-르메트르 법칙을 위한 방정식 v = H₀D 에 대입하여 알 수 있는 것처럼 지구와 우리에게서 '현재로' 멀어지고 있는 은하 사이의 거리이다.

허블 부피

 이 부분의 본문은 en:Hubble volume입니다.

허블 부피는 때때로 ${\displaystyle cH_{0}^{-1}}$의 공변하는 크기를 갖는 우주 부피로 정의된다. 정확한 정의는 다양한데: 때때로 반지름이 ${\displaystyle cH_{0}^{-1}}$ 인 구의 부피, 또는 대안으로서 한 변이 ${\displaystyle cH_{0}^{-1}}$ 인 정육면체로 정의된다. 일부 우주론자들은 허블 부피라는 용어를, 그 반지름이 약 3배 더 크기는 하지만, 관측 가능한 우주의 부피를 참조하는데 사용하기도 한다.

허블 상수 결정하기

최근 조사에 대한 측정 불확실성을 포함한 허블 상수 값^[54]

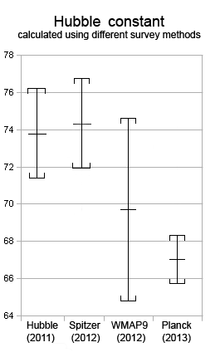
허블 상수의 값은 먼 은하의 적색편이를 측정한 다음 허블의 법칙이 아닌 다른 방법으로 거리를 결정함으로써 추정된다. 이 접근 방식은 은하 외 물체까지의 거리를 측정하기 위한 우주 거리 사다리의 일부를 형성한다. 이러한 거리를 결정하는 데 사용된 물리적 가정의 불확실성으로 인해 허블 상수에 대한 다양한 추정치가 발생했다.^[2]

허블 텐션

허블 상수를 결정하기 위해 여러 방법이 사용되었다. 보정된 거리 사다리 기술을 사용한 "후기 우주" 측정값은 약 73 km/s/Mpc의 값으로 수렴된다. 2000년 이후로 우주 마이크로파 배경 측정을 기반으로 한 "초기 우주" 기술이 사용 가능하게 되었으며 이는 67.7 km/s/Mpc 에 가까운 값에 일치한다. (이것은 초기 우주 이후의 팽창률의 변화를 설명하므로 첫 번째 숫자와 비슷하다.) 기술이 향상됨에 따라 추정 측정 불확실성(measurement uncertainty)은 줄어들었지만 측정 값의 범위는 줄어들지 않았다. 불일치는 이제 통계적으로 유의미하다. 이 불일치는 허블 텐션(Hubble tension)이라고 불린다.^[55][56]

2021년 12월 내셔널 지오그래픽은 허블 텐션 불일치의 원인을 알 수 없다고 보도했다.^[57] 그러나 우주론 원리가 실패하면("ΛCDM 모형" 기사의 "우주론 원리 위배" 참조) 허블 상수와 허블 텐션에 대한 기존 해석을 수정해야 한다.^[58]

한 가지 가능성은 허블 장력이 KBC 거시공동에 의해 발생한다는 것인데, 보이드 내부의 은하 초신성을 측정하는 것이 허블 상수의 우주론적 측정치보다 허블 상수에 대해 더 큰 국지적 값을 산출할 것이라고 일부 저자가 예측했기 때문이다.^[59] 그러나 다른 연구에서는 주장된 저밀도의 규모가 반지름을 넘어 확장된 관측과 양립할 수 없음을 발견하여 관측에서 이에 대한 증거를 찾지 못했다.^[60] 이후 이 분석에서 중요한 결함이 지적되어 허블 텐션이 실제로 KBC 거시공동의 유출로 인해 발생했을 가능성을 열어 두었다.^[61]

또 다른 가능성은 허블 장력이 ΛCDM 모델을 넘어서는 새로운 물리학을 요구한다는 것이다.^[56] 모리츠 하슬바우어_{Moritz Haslbauer}와 공동 연구자는 허블 텐션에 대한 가능한 해로 수정 뉴턴 역학을 제안했으며^[61], 마크 카미온코프스키_{Marc Kamionkowski}와 공동 연구자는 허블 텐션에 대한 가능한 해로로 초기 암흑 에너지 모형을 제안했다.^[62] 다른 이들은 텐션의 적어도 일부가 데이터의 불확실성을 과소평가한 결과일 수 있다고 제안했다.^[63][64]

초기 측정 및 논의 접근 방식

천문학자 발터 바데의 관찰은 그가 뚜렷한 별들을 위한 "종족"(종족I과 종족II)을 정의하도록 이끌었다. 같은 관측을 통해 그는 세페이드 변광성에는 두 가지 유형이 있다는 것을 발견했다. 이 발견을 통해 그는 1929년 허블이 계산한 우주의 크기를 두 배로 늘렸다.^[65][66][67] 그는 1952년 로마에서 열린 국제천문연맹 회의에서 이 결과를 발표하여 상당히 놀랐다.

20세기 후반의 대부분의 기간 동안 ${\displaystyle H_{0}}$의 값은 50과 90 (km/s)/Mpc 사이로서 추정되었다.

허블 상수의 값은 값이 약 100이라고 주장한 제라르 드보쿨뢰르와 값이 50에 가깝다고 주장한 앨런 샌디지_{Allan Sandage} 사이에 길고 다소 격렬한 논쟁의 주제였다.^[68] 당사자들 사이에 공유된 독설의 한 데모에서 샌디지와 [[w:Gustav Andreas Tammann|구스타프 안드레아스 탐만_{Gustav Andreas Tammann}(샌디지의 연구 동료)이 1975년에 그들의 방법의 체계적 오류를 확인하는 단점을 공식적으로 인정했을 때 드보쿨뢰르는 다음과 같이 응답했다. "대부분의 천문학자와 교과서 저술가들이 이 진지한 경고를 너무 빨리 잊고 무시한 것은 유감이다."^[69] 1996년에 존 바콜_{John Bahcall}이 중재한 시드니 반 덴 버그_{Sidney van den Bergh}와 구스타프 탐만_{Gustav Tammann} 사이의 토론은 이 두 경쟁 가치에 대한 초기 섀플리-커티스 논쟁과 유사한 방식으로 진행되었다.

이전에 추정치의 이 넓은 편차는 1990년대 후반에 우주의 ΛCDM 모형이 도입되면서 부분적으로 해결되었다. 수냐에프-젤도비치 효과를 사용하여 X선 및 마이크로파 파장에서 높은 적색편이 클러스터에 대한 ΛCDM 모델 관찰, 우주 마이크로파 배경 복사의 등방성 측정 및 광학 조사는 모두 상수에 대해 약 70의 값을 제공했다.

21세기 측정

Planck(2018) 및 SH0ES(2020) 값이 각각 분홍색과 청록색으로 강조 표시된 2021년경 H0 측정의 풍경^[56]

2018년에 발표된 플랑크 미션의 최근 측정값은 67.66±0.42 (km/s)/Mpc의 더 낮은 값을 나타낸다. 2019년 3월, 허블 우주 망원경과 관련된 개선된 절차를 사용하여 74.03±1.42 (km/s)/Mpc의 더 높은 값이 결정되었다.^[70] 두 측정값은 4.4σ 수준에서 일치하지 않으며 그럴듯한 확률 수준을 넘어선다.^[71] 이 불일치에 대한 해결책은 현재 진행 중인 활발한 연구 분야이다.^[72]

2018년 10월, 과학자들은 허블 상수를 결정하는 중력파 사건(특히 GW170817과 같은 중성자별의 병합(neutron star merger)과 관련된 사건)의 정보를 이용하여 새로운 세 번째 방법(두가지 초기 방법들, 적색편이에 기초한 방법과 우주 거리 사다리에 의한 다른 방법은 서로 일치하지 않는 결과를 제공했다.)을 제시했다.^[73][74]

2019년 7월, 천문학자들은 다크 사이렌(dark siren)으로 알진 GW170817의 중성자별 병합이 감지된 후 중성자별 쌍의 병합을 기반으로 허블 상수를 결정하고 이전 방법의 불일치를 해결하는 새로운 방법이 제안되었다고 보고했다.^[75][76] 그들의 허블 상수의 측정값은 73.3+5.3
−5.0 (km/s)/Mpc이다.^[77]

또한 2019년 7월에 천문학자들은 허블 우주 망원경의 데이터를 사용하고 적색거성가지의 첨단부(TRGB)를 사용하여 계산된 적색거성까지의 거리를 기반으로 하는 또 다른 새로운 방법을 보고했다. 그들의 허블 상수의 측정값은 69.8+1.9
−1.9 (km/s)/Mpc이다.^[78][79][80]

2020년 2월, 메가메이저(Megamaser) 우즈론 프로젝트는 거리 사다리 결과를 확인하고 95%의 통계적 유의 수준에서 초기 우주 결과와 다른 독립적인 결과를 발표했다.^[81] 2020년 7월, 아타카마 우주론 망원경(Atacama Cosmology Telescope)이 우주 배경 복사를 측정한 결과 우주가 현재 관측되는 것보다 더 느리게 팽창해야 한다고 예측했다.^[82]

허블 상수의 추정값, 2001-2020. 검은색 추정치는 73 km/s/Mpc 주위에 클러스터링되는 경향이 있는 보정된 거리 사다리 측정을 나타낸다. 빨간색은 67 km/s/Mpc 근처의 수치와 잘 일치하는 ΛCDM 매개변수를 사용한 초기 우주 CMB/BAO 측정을 나타내며, 반면에 파란색은 그 불확실성이 아직 둘 사이를 결정하기에 충분히 작지 않은 다른 테크닉들이다.

허블 상수의 측정

발표날짜 published	허블 상수 (km/s)/Mpc	관측 주체	인용 citation	언급 / 방법론
2023-05-11	66.6+4.1 −3.3	P. L. 켈리Kelly 외.	[83]	초신성 Refsdal의 중력 렌즈 이미지의 타이밍 지연. 우주 거리 사다리 또는 CMB와 무관하다.
2022-12-12	68.3±1.5	SPT-3G	[84]	CMB TT/TE/EE 파워 스펙트럼. 플랑크와 1σ 미만의 불일치. (사전 인쇄)
2022-02-08	73.4+0.99 −1.22	Pantheon+	[85]	Ia형 초신성 거리 사다리 (+SH0ES)
2022-06-17	75.4+3.8 −3.7	T. 드 예거de Jaeger 외.	[86]	II형 초신성을 표준화할 수 있는 촉광으로 사용하여 허블 상수를 독립적으로 측정—세페이드 변광성, 적색거성가지의 첨단부, 기하학적 거리(NGC 4258)에서 측정한 호스트 은하와 있는 13 SNe II-
2021-12-08	73.04±1.04	SH0ES	[87]	세페이드-Ia형 초신성 거리 사다리 (HST+Gaia EDR3+"Pantheon+"). 5σ 플랑크와의 불일치
2021-09-17	69.8±1.7	W. 프리드먼Freedman	[88]	[적색거성가지의 첨단부]](TRGB) 거리 표시기 (HST+Gaia EDR3)
2020-12-16	72.1±2.0	허블 우주망원경 / Gaia EDR3	[89]	TRGB 거리 표시기를 사용하여 적색 거성에 대한 이전 작업을 Gaia EDR3에서 얻은 센타우루스자리 오메가의 시차 측정과 결합한다.
2020-12-15	73.2±1.3	허블 우주망원경 / Gaia EDR3	[90]	HST 측광학(photometry)과 우리 은하에 대한 Gaia EDR3 시차[세페이드의 조합으로 세페이드 광도 보정의 불확실성을 1.0%로 줄인다. ${\displaystyle H_{0}}$에 대한 값의 전반적인 불확실성은 1.8%이며, 알려진 세페이드 호스트로 알려진 은하에서 Ia형 초신성 샘플이 더 많을 경우 1.3%로 감소할 것으로 예상된다. SHoES(암흑 에너지 상태 방정식를 위한 초산성들, ${\displaystyle H_{0}}$)로 알려진 공동 연구의 연속.
2020-12-04	73.5±5.3	E. J. 백스터Baxter, B. D. 셔윈Sherwin	[91]	CMB의 중력 렌즈 효과는 중입자 음향 진동을 참조하지 않고 ${\displaystyle H_{0}}$를 추정하는 데 사용된다. 플랑크 데이터를 분석하는 대체 방법.
2020-11-25	71.8+3.9 −3.3	P. 덴젤Denzel 외.	[92]	8개의 4중 중력 렌즈 은하계는 "초기" 우주 추정치와 "후기" 우주 추정치 모두와 일치하여 5%의 정확도로 ${\displaystyle H_{0}}$를 결정하는 데 사용된다. 거리 사다리 및 우주 마이크로파 배경과 무관하다.
2020-11-07	67.4 ± 1.0	T. 세지윅Sedgwick 외.	[93]	88 0.02 < ${\displaystyle z}$ < 0.05에서 파생된 표준 촉광 거리 표시기로 사용되는 Ia형 초신성에서 유도됨. ${\displaystyle H_{0}}$ 추정치는 은하 밀도장에서 추정한 대로 초신성 환경에서 고유 속도의 영향에 대해 수정되었다. 결과는 Ωm = 0.3, ΩΛ = 0.7 그리고 앤더슨Anderson 외. (2014)에서 가져온 값인 149.3Mpc의 음향 지평선을 가정한다.[94]
2020-09-29	67.6+4.3 −4.2	S. 무케르지Mukherjee et al.	[95]	중력파는 츠비키 과도기 시설(Zwicky Transient Facility)에 의해 발견된 과도 ZTF19abanrh가 GW190521에 대한 광학 대응물이라고 가정한다. 거리 사다리 및 우주 마이크로파 배경과 무관하다.
2020-06-18	75.8+5.2 −4.9	T. 드 예거 외.	[96]	세페이드 변광성 또는 적색거성가지의 첨단부에서 측정된 호스트-은하 거리와 함께 허블 상수의 독립적인 측정값을 얻기 위해 II형 초신성을 표준화 가능한 촉광으로 사용한다.
2020-02-26	73.9±3.0	메가마이저(Megamaser) 우주론 프로젝트	[81]	메가마이저(Megamaser) 호스팅 은하에 대한 기하학적 거리 측정. 거리 사다리 및 우주 마이크로파 배경과 무관하다.
2019-10-14	74.2+2.7 −3.0	STRIDES	[97]	렌즈된 퀘이사 DES J0408-5354의 질량 분포 및 시간 지연 모델링.
2019-09-12	76.8±2.6	SHARP/H0LiCOW	[98]	지상 기반 적응 광학 및 허블 우주 망원경을 사용하여 3개의 렌즈화된 은하계 개체와 해당 렌즈를 모델링한다.
2019-08-20	73.3+1.36 −1.35	K. 두타Dutta 외.	[99]	이 ${\displaystyle H_{0}}$는 ΛCDM 모델 내에서 낮은 적색편이 우주 데이터를 분석하여 얻은 것이다. 사용된 데이터 세트는 Ia형 초신성, 중입자 음향 진동, 강력한 렌즈를 사용한 시간 지연 측정, 우주 크로노미터를 사용한 ${\displaystyle H(z)}$ 측정 및 거대구조 관측으로부터의 성장 측정이다.
2019-08-15	73.5±1.4	M. J. 리드Reid, D. W. 페스Pesce, A. G. 리스Riess	[100]	초대형 블랙홀을 사용하여 메시에 106까지의 거리를 측정하고 대마젤란운에서 일식 바이너리 측정과 결합된다.
2019-07-16	69.8±1.9	허블 우주망원경	[78][79][80]	적색 거성까지의 거리는 TRGB 거리 표시기를 사용하여 계산된다.
2019-07-10	73.3+1.7 −1.8	H0LiCOW 공동 연구	[101]	우주 거리 사다리와 우주 마이크로파 배경 측정과는 독립적으로 이제 6개의 퀘이사를 사용하는 다중 이미지 퀘이사에 대한 업데이트된 관측.
2019-07-08	70.3+5.3 −5.0	LIGO 및 Virgo 탐지기	[77]	이전 중력파(GW) 및 전자기(EM) 데이터와 결합된 GW170817의 무선 대응물을 사용한다.
2019-03-28	68.0+4.2 −4.1	페르미 감마선 우주망원경	[102]	외부은하의 빛으로 인한 감마선 감쇠. 우주 거리 사다리와 우주 마이크로파 배경과는 무관하다.
2019-03-18	74.03±1.42	허블 우주망원경	[71]	대마젤란운(LMC)에서 세페이드의 정밀 HST 측광은 LMC까지의 거리에 대한 불확실성을 2.5%에서 1.3%로 줄인다. 개정판은 CMB 측정의 텐션을 4.4σ 수준(가우시안 오류의 경우 P=99.999%)으로 증가시켜 그럴듯한 수준 이상의 불일치를 높였다. SHoES 공동 연구의 연속이다.
2019-02-08	67.78+0.91 −0.87	조지프 라이언Joseph Ryan 외.	[103]	평평한 ΛCDM 모형을 가정한 퀘이사 각도 크기 및 중입자 음향 진동. 대안 모형은 허블 상수에 대해 다른(일반적으로 더 낮은) 값을 생성한다.
2018-11-06	67.77±1.30	암흑 에너지 탐사(DES)	[104]	중입자 음향 진동에 기반한 역 거리 사다리 방법을 사용한 초신성 측정.
2018-09-05	72.5+2.1 −2.3	H0LiCOW 공동 연구	[105]	우주 거리 사다리와 우주 마이크로파 배경 측정과는 독립적인 다중 이미지 퀘이사의 관측.
2018-07-18	67.66±0.42	플랑크 미션	[106]	최종 플랑크 2018 결과.
2018-04-27	73.52±1.62	허블 우주망원경 및 Gaia	[107][108]	초기 Gaia 시차 측정과 함께 은하 세페이드의 추가 HST 측광학. 수정된 값은 3.8σ 수준에서 CMB 측정으로 텐션을 높인다. SHoES 공동 연구의 지속.
2018-02-22	73.45±1.66	허블 우주망원경	[109][110]	거리 사다리의 향상된 보정을 위한 은하 세페이드의 시차 측정; 이 값은 3.7σ 수준에서 CMB 측정치와의 불일치를 나타낸다. 불확실성은 Gaia 카탈로그의 최종 릴리스와 함께 1% 미만으로 감소할 것으로 예상된다. SHoES 공동 연구.
2017-10-16	70.0+12.0 −8.0	LIGO 과학적 공동 연구 및 Virgo 간섭계 공동 연구	[111]	표준 사이렌 일반적인 "표준 촉광" 기술과 독립적인 측정; 쌍성자 중성자별(BNS) 합병 GW170817의 중력파 분석은 우주적 규모까지의 광도 거리를 직접 추정했다. 향후 10년 동안 50개의 유사한 탐지가 예상되면 다른 방법론의 텐션을 중재할 수 있다.[112] 중성자별-블랙홀 합병(NSBH)의 탐지 및 분석은 BNS가 허용할 수 있는 것보다 더 큰 정밀도를 제공할 수 있다.[113]
2016-11-22	71.9+2.4 −3.0	허블 우주망원경	[114]	강한 중력 렌즈에 의해 생성된 멀리 떨어진 가변 소스의 여러 이미지 사이에 시간 지연을 사용한다. COSMOGRAIL의 Wellspring(H0LiCOW)에서 ${\displaystyle H_{0}}$ 렌즈로 알려진 공동 연구.
2016-08-04	76.2+3.4 −2.7	Cosmicflows-3	[115]	Tully-Fisher, 세페이드 변광성 및 Ia형 초신성을 포함한 다른 거리 방법과 적색편이를 비교한다. 데이터의 제한적인 추정치는 75±2의 더 정확한 값을 의미한다.
2016-07-13	67.6+0.7 −0.6	SDSS 3차 중입자진동 분광탐사(BOSS)	[116]	중입자 음향 진동. 확장 조사(eBOSS)는 2014년에 시작되어 2020년까지 진행될 예정이다. 확장 조사는 빅뱅 이후 30억년에서 80억년까지 우주가 중력의 감속 효과에서 벗어나 전환하는 시간을 탐색하도록 설계되었다.[117]
2016-05-17	73.24±1.74	허블 우주망원경	[118]	Ia형 초신성, 다가오는 Gaia 측정 및 기타 개선으로 불확실성이 두 배 이상 감소할 것으로 예상된다. SHoES 공동 연구.
2015-02	67.74±0.46	플랑크 미션	[119][120]	2014년 12월 1일 이탈리아 페라라에서 열린 회의에서 플랑크 전체 임무 분석 결과가 공개되었다. 2015년 2월 임무 결과를 자세히 설명하는 전체 문서 세트가 공개되었다.
2013-10-01	74.4±3.0	Cosmicflows-2	[121]	Tully-Fisher, 세페이드 변광성, Ia형 초신성을 포함한 다른 거리 방법과 적색편이를 비교한다.
2013-03-21	67.80±0.77	플랑크 미션	[54][122][123][124][125]	ESA 플랑크 탐사선는 2009년 5월에 발사되었다. 4년에 걸쳐 [ 고전자 이동설 트랜지스터(HEMT) 라디오미터(radiometer)와 볼로미터 기술로 WMAP보다 작은 규모로 CMB를 측정한다. 2013년 3월 21일, 플랑크 우주 탐사선 뒤에 있는 유럽 주도의 연구팀은 새로운 CMB 전천지도와 허블 상수 결정을 포함한 미션 데이터를 발표했다.
2012-12-20	69.32±0.80	WMAP (9년간), 다른 측정과 결합됨	[126]
2010	70.4+1.3 −1.4	WMAP (7년간), 다른 측정과 결합됨	[127]	이러한 값은 WMAP 및 기타 우주 데이터의 조합을 ΛCDM 모형의 가장 간단한 버전에 맞추는 데서 발생한다. 데이터가 보다 일반적인 버전에 적합한 경우 H0은 더 작고 불확실한 경향이 있다. 일부 모형은 63 (km/s)/Mpc에 가까운 값을 허용하지만, 일반적으로 약 67±4 (km/s)/Mpc[128]
2010	71.0±2.5	WMAP 단독 (7년간).	[127]
2009-02	70.5±1.3	WMAP (5년간), 다른 측정과 결합됨	[129]
2009-02	71.9+2.6 −2.7	WMAP 단독 (5년간)	[129]
2007	70.4+1.5 −1.6	WMAP (3년간), 다른 측정과 결합됨	[130]
2006-08	76.9+10.7 −8.7	찬드라 엑스선 관측선	[131]	수냐에프-젤도비치 효과와 은하단에 대한 찬드라 X선 관측을 결합했다. 플랑크 공동 연구 2013에서 테이블의 조정된 불확실성.[132]
2003	72 ± 5	WMAP (첫해) 단독	.[133]
2001-05	72±8	허블 우주망원경 주요 게획	[26]	이 프로젝트는 유사한 정확도를 가진 많은 은하단에 대한 수냐에프-젤도비치 효과 관측에 기반한 H0 측정과 일치하는 가장 정밀한 광학 결정을 확립했다.
1996년 이전	50–90 (est.)		[68]
1994	67 ± 7	1a형 초신성 광도 곡선 모양	[134]	SN 1a의 광도와 광도 곡선 모양 사이의 결정된 관계. 리스 등은 상수를 결정하기 위해 SN 1972E의 광도 곡선과 NGC 5253까지의 세페이드 거리의 비율을 사용했다.
1970년대 중반	100 ± 10	제라르 드 보클레르Gerard de Vaucouleurs	[69]	제라르 드 보클레르Gerard de Vaucouleurs는 그가 100 ± 10을 도출하기 위해 5배 더 많은 1차 지표, 10배 더 많은 보정 방법, 2차 지표, 3배 더 많은 은하 데이터 점을 사용했기 때문에 샌디지Sandage의 상수로부터 허블 상수의 정확도를 향상시켰다고 생각했다.
1970년대 초	≈ 55 (est.)	앨런 샌디지Allan Sandage와 구스타브 탐만Gustav Tammann	[135]
1958	75 (est.)	앨런 샌디지Allan Sandage	[136]	이것은 H0의 첫 번째 좋은 추정치였지만 합의가 이루어지기까지는 수십 년이 걸렸다.
1956	180	휴머슨Humason, 메이올Mayall과 샌디지	[135]
1929	500	에드윈 허블, 후커 망원경	[137][135][138]
1927	625	조르주 르메트르	[139]	우주 팽창의 징후로 최초의 측정 및 해석

같이 보기

• 우주의 가속 팽창
• 우주론
• 암흑 물질
• 일반 상대성 원리의 테스트(Tests of general relativity)

각주

1. "IAU members vote to recommend renaming the Hubble law as the Hubble–Lemaître law" (Press release). IAU. 29 October 2018.
2. Overbye, Dennis (20 February 2017). "Cosmos Controversy: The Universe Is Expanding, but How Fast?". New York Times.
3. Coles, P., ed. (2001). Routledge Critical Dictionary of the New Cosmology. Routledge. p. 202.
4. "Hubble Flow". The Swinburne Astronomy Online Encyclopedia of Astronomy. Swinburne University of Technology.
5. van den Bergh, S. (2011). "The Curious Case of Lemaitre's Equation No. 24". Journal of the Royal Astronomical Society of Canada. 105 (4): 151. arXiv:1106.1195.
6. Nussbaumer, H.; Bieri, L. (2011). "Who discovered the expanding universe?". The Observatory. 131 (6): 394–398. arXiv:1107.2281.
7. Way, M.J. (2013). "Dismantling Hubble's Legacy?". ASP Conference Proceedings. 471: 97–132. arXiv:1301.7294.
8. Friedman, A. (December 1922). "Über die Krümmung des Raumes". Zeitschrift für Physik. 10 (1): 377–386. (English translation in Friedman, A. (December 1999). "On the Curvature of Space". General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F.
9. Lemaître, G. (1927). "Un univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques". Annales de la Société Scientifique de Bruxelles A. 47: 49–59. Partially translated in Lemaître, G. (1931). "Expansion of the universe, A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra-galactic nebulae". Monthly Notices of the Royal Astronomical Society. 91 (5): 483–490.
10. Livio, M. (2011). "Lost in translation: Mystery of the missing text solved". Nature. 479 (7372): 171–3. Bibcode:2011Natur.479..171L.
11. Livio, M.; Riess, A. (2013). "Measuring the Hubble constant". Physics Today. 66 (10): 41. Bibcode:2013PhT....66j..41L.
12. Hubble, E. (1929). "A relation between distance and radial velocity among extra-galactic nebulae". Proceedings of the National Academy of Sciences. 15 (3): 168–73. Bibcode:1929PNAS...15..168H.
13. Slipher, V.M. (1917). "Radial velocity observations of spiral nebulae". The Observatory. 40: 304–306. Bibcode:1917Obs....40..304S.
14. Longair, M. S. (2006). The Cosmic Century. Cambridge University Press. p. 109.
15. Nussbaumer, Harry (2013). 'Slipher's redshifts as support for de Sitter's model and the discovery of the dynamic universe' In Origins of the Expanding Universe: 1912-1932. Astronomical Society of the Pacific. pp. 25–38. arXiv:1303.1814.
16. Overbye, Dennis (25 February 2019). "Have Dark Forces Been Messing With the Cosmos? – Axions? Phantom energy? Astrophysicists scramble to patch a hole in the universe, rewriting cosmic history in the process". The New York Times.
17. O'Raifeartaigh, Cormac (2013). The Contribution of V.M. Slipher to the discovery of the expanding universe in 'Origins of the Expanding Universe'. Astronomical Society of the Pacific. pp. 49–62. arXiv:1212.5499.
18. "Three steps to the Hubble constant". www.spacetelescope.org.
19. Slipher, V. M. (1913). "The Radial Velocity of the Andromeda Nebula". Lowell Observatory Bulletin. 1: 56–57. Bibcode:1913LowOB...2...56S.
20. 20] Slipher, V. M. (1915). "Spectrographic Observations of Nebulae". Popular Astronomy. 23: 21–24. Bibcode:1915PA.....23...21S.
21. Friedman, A. (1922). "Über die Krümmung des Raumes". Zeitschrift für Physik. 10 (1): 377–386. Translated in Friedmann, A. (1999). "On the Curvature of Space". General Relativity and Gravitation. 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F.
22. van den Bergh, Sydney (2011). "The Curious Case of Lemaître's Equation No. 24". Journal of the Royal Astronomical Society of Canada. 105 (4): 151. arXiv:1106.1195.
23. Block, David (2012). 'Georges Lemaitre and Stigler's law of eponymy' in Georges Lemaître: Life, Science and Legacy (Holder and Mitton ed.). Springer. pp. 89–96.
24. Sandage, Allan (December 1989). "Edwin Hubble 1889-1953". Journal of the Royal Astronomical Society of Canada. 83 (6): 351–362.
25. Keel, W. C. (2007). The Road to Galaxy Formation (2nd ed.). Springer. pp. 7–8.
26. Freedman, W. L.; et al. (2001). "Final results from the Hubble Space Telescope Key Project to measure the Hubble constant". The Astrophysical Journal. 553 (1): 47–72. arXiv:astro-ph/0012376.
27. Weinberg, S. (2008). Cosmology. Oxford University Press. p. 28.
28. Bunn, E. F. (2009). "The kinematic origin of the cosmological redshift". American Journal of Physics. 77 (8): 688–694. arXiv:0808.1081.
29. Kirshner, R. P. (2003). "Hubble's diagram and cosmic expansion". Proceedings of the National Academy of Sciences. 101 (1): 8–13. Bibcode:2003PNAS..101....8K.
30. "What is a Cosmological Constant?". Goddard Space Flight Center.
31. Isaacson, W. (2007). Einstein: His Life and Universe. Simon & Schuster. p. 354.
32. "Einstein's Biggest Blunder? Dark Energy May Be Consistent With Cosmological Constant". Science Daily. 28 November 2007.
33. Keel, W. C. (2007). The Road to Galaxy Formation (2nd ed.). Springer. pp. 7–8.
34. "Is the universe expanding faster than the speed of light?". Ask an Astronomer at Cornell University. Archived from the original on 23 November 2003.
35. Harrison, E. (1992). "The redshift-distance and velocity-distance laws". The Astrophysical Journal. 403: 28–31. Bibcode:1993ApJ...403...28H.
36. Madsen, M. S. (1995). The Dynamic Cosmos. CRC Press. p. 35.
37. Dekel, A.; Ostriker, J. P. (1999). Formation of Structure in the Universe. Cambridge University Press. p. 164.
38. Padmanabhan, T. (1993). Structure formation in the universe. Cambridge University Press. p. 58.
39. Sartori, L. (1996). Understanding Relativity. University of California Press. p. 163, Appendix 5B.
40. Sartori, L. (1996). Understanding Relativity. University of California Press. pp. 304–305.
41. "Introduction to Cosmology", Matts Roos
42. Scharping, Nathaniel (18 October 2017). "Gravitational Waves Show How Fast The Universe is Expanding". Astronomy.
43. Chase, S. I.; Baez, J. C. (2004). "Olbers' Paradox". The Original Usenet Physics FAQ.
44. Asimov, I. (1974). "The Black of Night". Asimov on Astronomy. Doubleday.
45. Croton, Darren J. (14 October 2013). "Damn You, Little h! (Or, Real-World Applications of the Hubble Constant Using Observed and Simulated Data)". Publications of the Astronomical Society of Australia. 30.
46. Peebles, P. J. E. (1993). Principles of Physical Cosmology. Princeton University Press.
47. Perlmutter, S. (2003). "Supernovae, Dark Energy, and the Accelerating Universe" (PDF). Physics Today. 56 (4): 53–60.
48. Carroll, Sean (2004). Spacetime and Geometry: An Introduction to General Relativity (illustrated ed.). San Francisco: Addison-Wesley. p. 328.
49. Heneka, C.; Amendola, L. (2018). "General modified gravity with 21cm intensity mapping: simulations and forecast". Journal of Cosmology and Astroparticle Physics. 2018 (10): 004. arXiv:1805.03629.
50. Tawfik, A.; Harko, T. (2012). "Quark-hadron phase transitions in the viscous early universe". Physical Review D. 85 (8): 084032. arXiv:1108.5697.
51. Tawfik, A. (2011). "The Hubble parameter in the early universe with viscous QCD matter and finite cosmological constant". Annalen der Physik. 523 (5): 423–434. arXiv:1102.2626.
52. Tawfik, A.; Wahba, M.; Mansour, H.; Harko, T. (2011). "Viscous quark-gluon plasma in the early universe". Annalen der Physik. 523 (3): 194–207. arXiv:1001.2814.
53. Hawley, John F.; Holcomb, Katherine A. (2005). Foundations of modern cosmology (2nd ed.). Oxford [u.a.]: Oxford Univ. Press. p. 304.
54. Bucher, P. A. R.; et al. (Planck Collaboration) (2013). "Planck 2013 results. I. Overview of products and scientific Results". Astronomy & Astrophysics. 571: A1. arXiv:1303.5062.
55. Mann, Adam (26 August 2019). "One Number Shows Something Is Fundamentally Wrong with Our Conception of the Universe - This fight has universal implications". Live Science.
56. di Valentino, Eleonora; et al. (2021). "In the realm of the Hubble tension—a review of solutions". Classical and Quantum Gravity. 38 (15): 153001. arXiv:2103.01183.
57. Gresko, Michael. "The universe is expanding faster than it should be". nationalgeographic.com. National Geographic.
58. Elcio Abdalla; Guillermo Franco Abellán; et al. (11 Mar 2022), "Cosmology Intertwined: A Review of the Particle Physics, Astrophysics, and Cosmology Associated with the Cosmological Tensions and Anomalies"], Journal of High Energy Astrophysics, 34: 49, arXiv:2203.06142v1.
59. Shanks, T; Hogarth, L M; Metcalfe, N (2019-03-21). "Gaia Cepheid parallaxes and 'Local Hole' relieve H 0 tension". Monthly Notices of the Royal Astronomical Society: Letters. 484 (1): L64–L68.
60. Kenworthy, W. D’Arcy; Scolnic, Dan; Riess, Adam (2019-04-24). "The Local Perspective on the Hubble Tension: Local Structure Does Not Impact Measurement of the Hubble Constant". The Astrophysical Journal. 875 (2): 145. arXiv:1901.08681.
61. Haslbauer, M; Banik, I; Kroupa, P (2020-12-21). "The KBC void and Hubble tension contradict LCDM on a Gpc scale - Milgromian dynamics as a possible solution". Monthly Notices of the Royal Astronomical Society. 499 (2): 2845–2883.
62. Poulin, Vivian; Smith, Tristan L.; Karwal, Tanvi; Kamionkowski, Marc (2019-06-04). "Early Dark Energy can Resolve the Hubble Tension". Physical Review Letters. 122 (22): 221301. arXiv:1811.04083.
63. Rameez, Mohamed; Sarkar, Subir (15 July 2021). "Is there really a Hubble tension?". Classical and Quantum Gravity. 38 (15): 154005.
64. Singh, Ritesh (28 October 2021). "Evidence for possible systematic underestimation of uncertainties in extragalactic distances and its cosmological implications". Astrophysics and Space Science. 366 (10): 99.
65. Baade W (1944) The resolution of Messier 32, NGC 205, and the central region of the Andromeda nebula. ApJ 100 137-146
66. Baade W (1956) The period-luminosity relation of the Cepheids. PASP 68 5-16
67. Allen, Nick. "Section 2: The Great Debate and the Great Mistake: Shapley, Hubble, Baade". The Cepheid Distance Scale: A History. Archived from the original on 10 December 2007.
68. Overbye, D. (1999). "Prologue". Lonely Hearts of the Cosmos (2nd ed.). HarperCollins. p. 1ff.
69. de Vaucouleurs, G. (1982). The cosmic distance scale and the Hubble constant. Mount Stromlo and Siding Spring Observatories, Australian National University.
70. Ananthaswamy, Anil (2019년 3월 22일). “Best-Yet Measurements Deepen Cosmological Crisis”. 《Scientific American》. 2019년 3월 23일에 확인함.
71. Millea, Marius; Knox, Lloyd (2019년 8월 10일). “The Hubble Hunter's Guide” (영어). arXiv:1908.03663v1 [astro-ph.CO].
72. Millea, Marius; Knox, Lloyd (2019-08-10). "The Hubble Hunter's Guide". arXiv:1908.03663v1 [astro-ph.CO].
73. Lerner, Louise (22 October 2018). "Gravitational waves could soon provide measure of universe's expansion". Phys.org.
74. Chen, Hsin-Yu; Fishbach, Maya; Holz, Daniel E. (17 October 2018). "A two per cent Hubble constant measurement from standard sirens within five years". Nature. 562 (7728): 545–547. arXiv:1712.06531.y
75. National Radio Astronomy Observatory (8 July 2019). "New method may resolve difficulty in measuring universe's expansion - Neutron star mergers can provide new 'cosmic ruler'". EurekAlert!.
76. Finley, Dave (8 July 2019). "New Method May Resolve Difficulty in Measuring Universe's Expansion". National Radio Astronomy Observatory.
77. Hotokezaka, K.; et al. (8 July 2019). "A Hubble constant measurement from superluminal motion of the jet in GW170817". Nature Astronomy. 3 (10): 940–944. arXiv:1806.10596.
78. Carnegie Institution of Science (16 July 2019). "New measurement of universe's expansion rate is 'stuck in the middle' - Red giant stars observed by Hubble Space Telescope used to make an entirely new measurement of how fast the universe is expanding". EurekAlert!.
79. Sokol, Joshua (19 July 2019). "Debate intensifies over speed of expanding universe". Science.
80. Wendy L. Freedman; Madore, Barry F.; Hatt, Dylan; Hoyt, Taylor J.; et al. (2019). "The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch". The Astrophysical Journal. 882 (1): 34. arXiv:1907.05922.
81. Pesce, D. W.; Braatz, J. A.; Reid, M. J.; Riess, A. G.; et al. (26 February 2020). "The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints". The Astrophysical Journal. 891 (1): L1. arXiv:2001.09213.
82. Castelvecchi, Davide (2020-07-15). "Mystery over Universe's expansion deepens with fresh data". Nature. 583 (7817): 500–501.
83. Kelly, P. L.; Rodney, S.; Treu, T.; Oguri, M.; Chen, W.; Zitri, A.; et al. (2023-05-11). "Constraints on the Hubble constant from Supernova Refsdal's reappearance". Science. 380 (6649): eabh1322. arXiv:2305.06367.
84. Balkenhol, L.; Dutcher, D.; Mancini, A. Spurio; Doussot, A.; Benabed, K.; Galli, S.; Ade, P. A. R.; Anderson, A. J.; Ansarinejad, B.; Archipley, M.; Bender, A. N.; Benson, B. A.; Bianchini, F.; Bleem, L. E.; Bouchet, F. R. (2022년 12월 14일). “A Measurement of the CMB Temperature Power Spectrum and Constraints on Cosmology from the SPT-3G 2018 TT/TE/EE Data Set”. arXiv:2212.05642.
85. Brout, Dillon; Scolnic, Dan; Popovic, Brodie; Riess, Adam G.; Carr, Anthony; Zuntz, Joe; Kessler, Rick; Davis, Tamara M.; Hinton, Samuel; Jones, David; Kenworthy, W. D'Arcy; Peterson, Erik R.; Said, Khaled; Taylor, Georgie; Ali, Noor; Armstrong, Patrick; Charvu, Pranav; Dwomoh, Arianna; Meldorf, Cole; Palmese, Antonella; Qu, Helen; Rose, Benjamin M.; Sanchez, Bruno; Stubbs, Christopher W.; Vincenzi, Maria; Wood, Charlotte M.; Brown, Peter J.; Chen, Rebecca; Chambers, Ken; Coulter, David A.; Dai, Mi; Dimitriadis, Georgios; Filippenko, Alexi V.; Foley, Ryan J.; Jha, Saurabh W.; Kelsey, Lisa; Kirshner, Robert P.; Möller, Anais; Muir, Jessie; Nadathur, Seshadri; Pan, Yen-Chen; Rest, Armin; Rojas-Bravo, Cesar; Sako, Masao; Siebert, Matthew R.; Smith, Mat; Stahl, Benjamin E.; Wiseman, Phil (2022년 2월 8일). “The Pantheon+ Analysis: Cosmological Constraints”. 《The Astrophysical Journal》 938 (2): 110. arXiv:2202.04077. Bibcode:2022ApJ...938..110B. doi:10.3847/1538-4357/ac8e04. S2CID 246679941.
86. de Jaeger, T.; Galbany, L.; Riess, A. G.; Stahl, Ben E.; 외. (2022년 6월 17일). “A 5 per cent measurement of the Hubble–Lemaître constant from Type II supernovae”. 《MNRAS》 514 (3): 4620–4628. arXiv:2203.08974. doi:10.1093/mnras/stac1661.
87. Riess, Adam G.; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan; Brout, Dillon; Casertano, Stefano; Jones, David O.; Murakami, Yukei; Breuval, Louise; Brink, Thomas G.; Filippenko, Alexei V. (2021년 12월 8일). “A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team”. 《The Astrophysical Journal》 934 (1). arXiv:2112.04510. Bibcode:2022ApJ...934L...7R. doi:10.3847/2041-8213/ac5c5b. S2CID 245005861.
88. Freedman, Wendy L. (2021년 9월 1일). “Measurements of the Hubble Constant: Tensions in Perspective*”. 《The Astrophysical Journal》 919 (1): 16. arXiv:2106.15656. Bibcode:2021ApJ...919...16F. doi:10.3847/1538-4357/ac0e95. ISSN 0004-637X. S2CID 235683396.
89. Soltis, J.; Casertano, S.; Riess, A. G. (2021). “The Parallax of Omega Centauri Measured from Gaia EDR3 and a Direct, Geometric Calibration of the Tip of the Red Giant Branch and the Hubble Constant”. 《The Astrophysical Journal》 908 (1): L5. arXiv:2012.09196. Bibcode:2021ApJ...908L...5S. doi:10.3847/2041-8213/abdbad. S2CID 229297709.
90. Riess, A. G.; Casertano, S.; Yuan, W.; Bowers, J. B.; 외. (2021). “Cosmic Distances Calibrated to 1% Precision with Gaia EDR3 Parallaxes and Hubble Space Telescope Photometry of 75 Milky Way Cepheids Confirm Tension with LambdaCDM”. 《The Astrophysical Journal》 908 (1): L6. arXiv:2012.08534. Bibcode:2021ApJ...908L...6R. doi:10.3847/2041-8213/abdbaf. S2CID 229213131.
91. Baxter, E. J.; Sherwin, B. D. (February 2021). “Determining the Hubble constant without the sound horizon scale: measurements from CMB lensing”. 《Monthly Notices of the Royal Astronomical Society》 501 (2): 1823–1835. arXiv:2007.04007. Bibcode:2021MNRAS.501.1823B. doi:10.1093/mnras/staa3706. S2CID 220404332.
92. Denzel, P.; Coles, J. P.; Saha, P.; Williams, L. L. R. (February 2021). “The Hubble constant from eight time-delay galaxy lenses”. 《Monthly Notices of the Royal Astronomical Society》 501 (1): 784–801. arXiv:2007.14398. Bibcode:2021MNRAS.501..784D. doi:10.1093/mnras/staa3603. S2CID 220845622.
93. Sedgwick, Thomas M; Collins, Chris A; Baldry, Ivan K; James, Philip A (2020년 11월 7일). “The effects of peculiar velocities in SN Ia environments on the local H0 measurement”. 《Monthly Notices of the Royal Astronomical Society》 500 (3): 3728–3742. arXiv:1911.03155. doi:10.1093/mnras/staa3456. ISSN 0035-8711.
94. Anderson, Lauren; Aubourg, Éric; Bailey, Stephen; Beutler, Florian; Bhardwaj, Vaishali; Blanton, Michael; Bolton, Adam S.; Brinkmann, J.; Brownstein, Joel R.; Burden, Angela; Chuang, Chia-Hsun (2014년 4월 21일). “The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: baryon acoustic oscillations in the Data Releases 10 and 11 Galaxy samples”. 《Monthly Notices of the Royal Astronomical Society》 441 (1): 24–62. doi:10.1093/mnras/stu523. hdl:2445/101758. ISSN 1365-2966.
95. Mukherjee, S.; Ghosh, A.; Graham, M. J.; Karathanasis, C.; 외. (2020년 9월 29일). “First measurement of the Hubble parameter from bright binary black hole GW190521”. arXiv:2009.14199.
96. de Jaeger, T.; Stahl, B.; Zheng, W.; Filippenko, A.V.; 외. (2020년 6월 18일). “A measurement of the Hubble constant from Type II supernovae”. 《MNRAS》 496 (3): 3402–3411. arXiv:2006.03412. doi:10.1093/mnras/staa1801.
97. Shajib, A. J.; Birrer, S.; Treu, T.; Agnello, A.; 외. (2019년 10월 14일). “STRIDES: A 3.9 per cent measurement of the Hubble constant from the strongly lensed system DES J0408-5354”. 《Monthly Notices of the Royal Astronomical Society》. arXiv:1910.06306. doi:10.1093/mnras/staa828. S2CID 204509190.
98. Chen, G.C.-F.; Fassnacht, C.D.; Suyu, S.H.; Rusu, C.E.; 외. (2019년 9월 12일). “A SHARP view of H0LiCOW: H0 from three time-delay gravitational lens systems with adaptive optics imaging”. 《Monthly Notices of the Royal Astronomical Society》 (영어) 490 (2): 1743–1773. arXiv:1907.02533. Bibcode:2019MNRAS.490.1743C. doi:10.1093/mnras/stz2547. S2CID 195820422.
99. Dutta, Koushik; Roy, Anirban; Ruchika, Ruchika; Sen, Anjan A.; Sheikh-Jabbari, M. M. (2019년 8월 20일). “Cosmology With Low-Redshift Observations: No Signal For New Physics”. 《Phys. Rev. D》 (영어) 100 (10): 103501. arXiv:1908.07267. Bibcode:2019PhRvD.100j3501D. doi:10.1103/PhysRevD.100.103501. S2CID 201107151.
100. Reid, M. J.; Pesce, D. W.; Riess, A. G. (2019년 8월 15일). “An Improved Distance to NGC 4258 and its Implications for the Hubble Constant”. 《The Astrophysical Journal》 (영어) 886 (2): L27. arXiv:1908.05625. Bibcode:2019ApJ...886L..27R. doi:10.3847/2041-8213/ab552d. S2CID 199668809.
101. Kenneth C. Wong (2020). “H0LiCOW XIII. A 2.4% measurement of H₀ from lensed quasars: 5.3σ tension between early and late-Universe probes”. 《Monthly Notices of the Royal Astronomical Society》. arXiv:1907.04869. doi:10.1093/mnras/stz3094. S2CID 195886279.
102. Domínguez, Alberto; 외. (2019년 3월 28일). “A new measurement of the Hubble constant and matter content of the Universe using extragalactic background light γ-ray attenuation”. 《The Astrophysical Journal》 885 (2): 137. arXiv:1903.12097. Bibcode:2019ApJ...885..137D. doi:10.3847/1538-4357/ab4a0e. S2CID 85543845.
103. Ryan, Joseph; Chen, Yun; Ratra, Bharat (2019년 2월 8일). “Baryon acoustic oscillation, Hubble parameter, and angular size measurement constraints on the Hubble constant, dark energy dynamics, and spatial curvature”. 《Monthly Notices of the Royal Astronomical Society》 488 (3): 3844–3856. arXiv:1902.03196. Bibcode:2019MNRAS.488.3844R. doi:10.1093/mnras/stz1966. S2CID 119226802.
104. Macaulay, E; 외. (DES collaboration) (2018). “First Cosmological Results using Type Ia Supernovae from the Dark Energy Survey: Measurement of the Hubble Constant”. 《Monthly Notices of the Royal Astronomical Society》 486 (2): 2184–2196. arXiv:1811.02376. doi:10.1093/mnras/stz978. S2CID 119310644.
105. Birrer, S; Treu, T; Rusu, C. E; Bonvin, V; 외. (2018). “H0LiCOW - IX. Cosmographic analysis of the doubly imaged quasar SDSS 1206+4332 and a new measurement of the Hubble constant”. 《Monthly Notices of the Royal Astronomical Society》 484 (4): 4726–4753. arXiv:1809.01274. Bibcode:2019MNRAS.484.4726B. doi:10.1093/mnras/stz200. S2CID 119053798.
106. Planck Collaboration; Aghanim, N.; 외. (2018). “Planck 2018 results. VI. Cosmological parameters”. arXiv:1807.06209. Bibcode:2018arXiv180706209P.
107. Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; 외. (2018). “Milky Way Cepheid Standards for Measuring Cosmic Distances and Application to Gaia DR2: Implications for the Hubble Constant”. 《The Astrophysical Journal》 (영어) 861 (2): 126. arXiv:1804.10655. Bibcode:2018ApJ...861..126R. doi:10.3847/1538-4357/aac82e. ISSN 0004-637X. S2CID 55643027.
108. Devlin, Hannah (2018년 5월 10일). “The answer to life, the universe and everything might be 73. Or 67”. 《the Guardian》 (영어). 2018년 5월 13일에 확인함.
109. Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas; 외. (2018년 2월 22일). “New parallaxes of galactic Cepheids from spatially scanning the Hubble Space Telescope: Implications for the Hubble constant” (PDF). 《The Astrophysical Journal》 855 (2): 136. arXiv:1801.01120. Bibcode:2018ApJ...855..136R. doi:10.3847/1538-4357/aaadb7. S2CID 67808349. 2022년 10월 9일에 원본 문서 (PDF)에서 보존된 문서. 2018년 2월 23일에 확인함.
110. Weaver, Donna; Villard, Ray; Hille, Karl (2018년 2월 22일). “Improved Hubble Yardstick Gives Fresh Evidence for New Physics in the Universe”. 《NASA》. 2018년 2월 24일에 확인함.
111. The LIGO Scientific Collaboration and The Virgo Collaboration; The 1M2H Collaboration; The Dark Energy Camera GW-EM Collaboration and the DES Collaboration; The DLT40 Collaboration; 외. (2017년 10월 16일). “A gravitational-wave standard siren measurement of the Hubble constant” (PDF). 《Nature》 (영어) 551 (7678): 85–88. arXiv:1710.05835. Bibcode:2017Natur.551...85A. doi:10.1038/nature24471. ISSN 1476-4687. PMID 29094696. S2CID 205261622. 2022년 10월 9일에 원본 문서 (PDF)에서 보존된 문서.
112. Feeney, Stephen M; Peiris, Hiranya V; Williamson, Andrew R; Nissanke, Samaya M; 외. (2019). “Prospects for resolving the Hubble constant tension with standard sirens”. 《Physical Review Letters》 122 (6): 061105. arXiv:1802.03404. Bibcode:2019PhRvL.122f1105F. doi:10.1103/PhysRevLett.122.061105. PMID 30822066. S2CID 73493934.
113. Vitale, Salvatore; Chen, Hsin-Yu (2018년 7월 12일). “Measuring the Hubble Constant with Neutron Star Black Hole Mergers”. 《Physical Review Letters》 121 (2): 021303. arXiv:1804.07337. Bibcode:2018PhRvL.121b1303V. doi:10.1103/PhysRevLett.121.021303. PMID 30085719. S2CID 51940146.
114. Bonvin, Vivien; Courbin, Frédéric; Suyu, Sherry H.; 외. (2016년 11월 22일). “H0LiCOW – V. New COSMOGRAIL time delays of HE 0435−1223: H₀ to 3.8 per cent precision from strong lensing in a flat ΛCDM model”. 《MNRAS》 465 (4): 4914–4930. arXiv:1607.01790. Bibcode:2017MNRAS.465.4914B. doi:10.1093/mnras/stw3006. S2CID 109934944.
115. Tully, R. Brent; Courtois, Hélène M.; Sorce, Jenny G. (2016년 8월 3일). “COSMICFLOWS-3”. 《The Astronomical Journal》 152 (2): 50. arXiv:1605.01765. Bibcode:2016AJ....152...50T. doi:10.3847/0004-6256/152/2/50. S2CID 250737862.
116. Grieb, Jan N.; Sánchez, Ariel G.; Salazar-Albornoz, Salvador (2016년 7월 13일). “The clustering of galaxies in the completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological implications of the Fourier space wedges of the final sample”. 《Monthly Notices of the Royal Astronomical Society》 467 (2): stw3384. arXiv:1607.03143. Bibcode:2017MNRAS.467.2085G. doi:10.1093/mnras/stw3384. S2CID 55888085.
117. “The Extended Baryon Oscillation Spectroscopic Survey (eBOSS)”. 《SDSS》. 2018년 5월 13일에 확인함.
118. Riess, Adam G.; Macri, Lucas M.; Hoffmann, Samantha L.; Scolnic, Dan; 외. (2016년 4월 5일). “A 2.4% Determination of the Local Value of the Hubble Constant”. 《The Astrophysical Journal》 826 (1): 56. arXiv:1604.01424. Bibcode:2016ApJ...826...56R. doi:10.3847/0004-637X/826/1/56. S2CID 118630031.
119. “Planck Publications: Planck 2015 Results”. European Space Agency. February 2015. 2015년 2월 9일에 확인함.
120. Cowen, Ron; Castelvecchi, Davide (2014년 12월 2일). “European probe shoots down dark-matter claims”. 《Nature》. doi:10.1038/nature.2014.16462. 2014년 12월 6일에 확인함.
121. Tully, R. Brent; Courtois, Helene M.; Dolphin, Andrew E.; Fisher, J. Richard; 외. (2013년 9월 5일). “Cosmicflows-2: The Data”. 《The Astronomical Journal》 146 (4): 86. arXiv:1307.7213. Bibcode:2013AJ....146...86T. doi:10.1088/0004-6256/146/4/86. ISSN 0004-6256. S2CID 118494842.
122. “Planck reveals an almost perfect universe”. ESA. 2013년 3월 21일. 2013년 3월 21일에 확인함.
123. “Planck Mission Brings Universe Into Sharp Focus”. JPL. 2013년 3월 21일. 2013년 3월 21일에 확인함.
124. Overbye, D. (2013년 3월 21일). “An infant universe, born before we knew”. 《New York Times》. 2013년 3월 21일에 확인함.
125. Boyle, A. (2013년 3월 21일). “Planck probe's cosmic 'baby picture' revises universe's vital statistics”. 《NBC News》. 2013년 3월 23일에 원본 문서에서 보존된 문서. 2013년 3월 21일에 확인함.
126. Bennett, C. L.; 외. (2013). “Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Final maps and results”. 《The Astrophysical Journal Supplement Series》 208 (2): 20. arXiv:1212.5225. Bibcode:2013ApJS..208...20B. doi:10.1088/0067-0049/208/2/20. S2CID 119271232.
127. Jarosik, N.; 외. (2011). “Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: Sky maps, systematic errors, and basic results”. 《The Astrophysical Journal Supplement Series》 192 (2): 14. arXiv:1001.4744. Bibcode:2011ApJS..192...14J. doi:10.1088/0067-0049/192/2/14. S2CID 46171526.
128. Results for H₀ and other cosmological parameters obtained by fitting a variety of models to several combinations of WMAP and other data are available at the NASA's LAMBDA website 보관됨 2014-07-09 - 웨이백 머신.
129. Hinshaw, G.; et al. (WMAP Collaboration) (2009). “Five-year Wilkinson Microwave Anisotropy Probe observations: Data processing, sky maps, and basic results”. 《The Astrophysical Journal Supplement》 180 (2): 225–245. arXiv:0803.0732. Bibcode:2009ApJS..180..225H. doi:10.1088/0067-0049/180/2/225. S2CID 3629998.
130. Spergel, D. N.; et al. (WMAP Collaboration) (2007). “Three-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Implications for cosmology”. 《The Astrophysical Journal Supplement Series》 170 (2): 377–408. arXiv:astro-ph/0603449. Bibcode:2007ApJS..170..377S. doi:10.1086/513700. S2CID 1386346.
131. Bonamente, M.; Joy, M. K.; Laroque, S. J.; Carlstrom, J. E.; 외. (2006). “Determination of the cosmic distance scale from Sunyaev–Zel'dovich effect and Chandra X‐ray measurements of high‐redshift galaxy clusters”. 《The Astrophysical Journal》 647 (1): 25. arXiv:astro-ph/0512349. Bibcode:2006ApJ...647...25B. doi:10.1086/505291. S2CID 15723115.
132. Planck Collaboration (2013). “Planck 2013 results. XVI. Cosmological parameters”. 《Astronomy & Astrophysics》 571: A16. arXiv:1303.5076. Bibcode:2014A&A...571A..16P. doi:10.1051/0004-6361/201321591. S2CID 118349591.
133. Spergel, D.N. (September 2003). “First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters”. 《The Astrophysical Journal Supplement Series》 148 (1): 175–194. arXiv:astro-ph/0302209. Bibcode:2003ApJS..148..175S. doi:10.1086/377226. S2CID 10794058.
134. Riess, Adam G. (January 1995). “Using SN Ia Light Curve Shapes to Measure The Hubble Constant”. 《The Astrophysical Journal》 438 (L17). arXiv:astro-ph/9410054. doi:10.1086/187704. S2CID 118938423.
135. John P. Huchra (2008). “The Hubble Constant”. 《Harvard Center for Astrophysics》.
136. Sandage, A. R. (1958). “Current problems in the extragalactic distance scale”. 《The Astrophysical Journal》 127 (3): 513–526. Bibcode:1958ApJ...127..513S. doi:10.1086/146483.
137. Edwin Hubble, A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae, Proceedings of the National Academy of Sciences, vol. 15, no. 3, pp. 168-173, March 1929
138. “Hubble's Constant”. 《Skywise Unlimited - Western Washington University》.
139. Lemaître, Georges (1927). “Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques”. 《Annales de la Société Scientifique de Bruxelles》 (프랑스어) A47: 49–59. Bibcode:1927ASSB...47...49L.

참고 문헌

• Hubble, E. P. (1937). The Observational Approach to Cosmology. Clarendon Press.
• Kutner, M. (2003). Astronomy: A Physical Perspective. Cambridge University Press.
• Liddle, A. R. (2003). An Introduction to Modern Cosmology (2nd ed.). John Wiley & Sons.

추가 자료

• Freedman, W. L.; Madore, B. F. (2010). "The Hubble Constant". Annual Review of Astronomy and Astrophysics. 48: 673–710. arXiv:1004.1856.

외부 링크

• NASA's WAMP - Big Bang Expansion: the Hubble Constant
• The Hubble Key Project
• The Hubble Diagram Project
• Coming to terms with different Hubble Constants (Forbes; 3 May 2019)
• Merrifield, Michael (2009). "Hubble Constant". Sixty Symbols. Brady Haran for University of Nottingham.

추가 링크

• Hubble's quantum law.
• 현대 우주론 Modern Cosmology: The Study of the Universe (2017-) Archived 2022년 9월 26일 - 웨이백 머신 by Kwanseok Kim