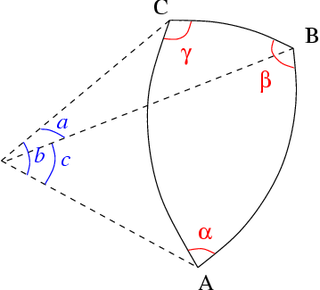
구면 삼각형의 세 각
A
,
B
,
C
{\displaystyle A,B,C}
a
,
b
,
c
{\displaystyle a,b,c}
단위 구면 위의 구면 삼각형
A
B
C
{\displaystyle ABC}
A
,
B
,
C
{\displaystyle A,B,C}
a
,
b
,
c
{\displaystyle a,b,c}
cos
c
=
cos
a
cos
b
+
sin
a
sin
b
cos
C
{\displaystyle \cos c=\cos a\cos b+\sin a\sin b\cos C}
여기서
cos
,
sin
{\displaystyle \cos ,\sin }
코사인 , 사인 이다. 이를 (제1) 구면 코사인 법칙 (第一球面cosine法則, 영어 : (first) spherical law of cosines )이라고 한다. 이에 대한 쌍대 명제는 다음과 같다.
cos
C
=
−
cos
A
cos
B
+
sin
A
sin
B
cos
c
{\displaystyle \cos C=-\cos A\cos B+\sin A\sin B\cos c}
이를 제2 구면 코사인 법칙 (第二球面cosine法則, 영어 : second spherical law of cosines )이라고 한다.
이 둘은 각각 다음과 같이 쓸 수 있다.
cos
C
=
cos
c
−
cos
a
cos
b
sin
a
sin
b
{\displaystyle \cos C={\frac {\cos c-\cos a\cos b}{\sin a\sin b}}}
cos
c
=
cos
C
+
cos
A
cos
B
sin
A
sin
B
{\displaystyle \cos c={\frac {\cos C+\cos A\cos B}{\sin A\sin B}}}
다음과 같은 벡터들을 정의하자.
u
=
O
A
→
−
(
O
C
→
⋅
O
A
→
)
O
C
→
|
O
A
→
−
(
O
C
→
⋅
O
A
→
)
O
C
→
|
,
v
=
O
B
→
−
(
O
C
→
⋅
O
B
→
)
O
C
→
|
O
B
→
−
(
O
C
→
⋅
O
B
→
)
O
C
→
|
{\displaystyle \mathbf {u} ={\frac {{\overrightarrow {OA}}-({\overrightarrow {OC}}\cdot {\overrightarrow {OA}}){\overrightarrow {OC}}}{|{\overrightarrow {OA}}-({\overrightarrow {OC}}\cdot {\overrightarrow {OA}}){\overrightarrow {OC}}|}},\;\mathbf {v} ={\frac {{\overrightarrow {OB}}-({\overrightarrow {OC}}\cdot {\overrightarrow {OB}}){\overrightarrow {OC}}}{|{\overrightarrow {OB}}-({\overrightarrow {OC}}\cdot {\overrightarrow {OB}}){\overrightarrow {OC}}|}}}
즉,
u
,
v
{\displaystyle \mathbf {u} ,\mathbf {v} }
C
{\displaystyle C}
A
,
B
{\displaystyle A,B}
접벡터 이다. 그렇다면,
u
,
v
{\displaystyle \mathbf {u} ,\mathbf {v} }
C
{\displaystyle C}
{
O
C
→
,
u
}
,
{
O
C
→
,
v
}
{\displaystyle \{{\overrightarrow {OC}},\mathbf {u} \},\{{\overrightarrow {OC}},\mathbf {v} \}}
O
A
C
,
O
A
B
{\displaystyle OAC,OAB}
정규 직교 기저 를 이루므로,
O
A
→
,
O
B
→
{\displaystyle {\overrightarrow {OA}},{\overrightarrow {OB}}}
O
A
→
=
cos
a
⋅
O
C
→
+
sin
a
⋅
u
{\displaystyle {\overrightarrow {OA}}=\cos a\cdot {\overrightarrow {OC}}+\sin a\cdot \mathbf {u} }
O
B
→
=
cos
b
⋅
O
C
→
+
sin
b
⋅
v
{\displaystyle {\overrightarrow {OB}}=\cos b\cdot {\overrightarrow {OC}}+\sin b\cdot \mathbf {v} }
따라서, 다음이 성립한다.
cos
c
=
O
A
→
⋅
O
B
→
=
(
cos
a
⋅
O
C
→
+
sin
a
⋅
u
)
⋅
(
cos
b
⋅
O
C
→
+
sin
b
⋅
v
)
=
cos
a
cos
b
+
sin
a
sin
b
cos
C
{\displaystyle {\begin{aligned}\cos c&={\overrightarrow {OA}}\cdot {\overrightarrow {OB}}\\&=(\cos a\cdot {\overrightarrow {OC}}+\sin a\cdot \mathbf {u} )\cdot (\cos b\cdot {\overrightarrow {OC}}+\sin b\cdot \mathbf {v} )\\&=\cos a\cos b+\sin a\sin b\cos C\end{aligned}}}
단위 구면의 중심을
O
{\displaystyle O}
a
=
O
A
→
,
b
=
O
B
→
,
c
=
O
C
→
{\displaystyle \mathbf {a} ={\overrightarrow {OA}},\;\mathbf {b} ={\overrightarrow {OB}},\;\mathbf {c} ={\overrightarrow {OC}}}
그렇다면,
a
,
b
,
c
{\displaystyle \mathbf {a} ,\mathbf {b} ,\mathbf {c} }
a
,
b
{\displaystyle \mathbf {a} ,\mathbf {b} }
c
{\displaystyle c}
a
,
c
{\displaystyle \mathbf {a} ,\mathbf {c} }
b
{\displaystyle b}
b
,
c
{\displaystyle \mathbf {b} ,\mathbf {c} }
a
{\displaystyle a}
벡터곱
a
×
b
{\displaystyle \mathbf {a} \times \mathbf {b} }
a
×
c
{\displaystyle \mathbf {a} \times \mathbf {c} }
b
×
c
{\displaystyle \mathbf {b} \times \mathbf {c} }
sin
c
{\displaystyle \sin c}
sin
b
{\displaystyle \sin b}
sin
a
{\displaystyle \sin a}
a
×
b
{\displaystyle \mathbf {a} \times \mathbf {b} }
a
×
c
{\displaystyle \mathbf {a} \times \mathbf {c} }
A
{\displaystyle A}
b
×
a
{\displaystyle \mathbf {b} \times \mathbf {a} }
b
×
c
{\displaystyle \mathbf {b} \times \mathbf {c} }
B
{\displaystyle B}
c
×
a
{\displaystyle \mathbf {c} \times \mathbf {a} }
c
×
b
{\displaystyle \mathbf {c} \times \mathbf {b} }
C
{\displaystyle C}
비네-코시 항등식 에 따라 다음이 성립함에 주의하자.
(
c
×
b
)
⋅
(
c
×
a
)
=
(
c
⋅
c
)
(
a
⋅
b
)
−
(
c
⋅
b
)
(
c
⋅
a
)
{\displaystyle (\mathbf {c} \times \mathbf {b} )\cdot (\mathbf {c} \times \mathbf {a} )=(\mathbf {c} \cdot \mathbf {c} )(\mathbf {a} \cdot \mathbf {b} )-(\mathbf {c} \cdot \mathbf {b} )(\mathbf {c} \cdot \mathbf {a} )}
여기에 위의 결과들을 대입하면 다음을 얻는다.
sin
a
sin
b
cos
C
=
cos
c
−
cos
a
cos
b
{\displaystyle \sin a\sin b\cos C=\cos c-\cos a\cos b}
이로써 제1 구면 코사인 법칙이 증명된다.
구면 삼각형
A
B
C
{\displaystyle ABC}
극삼각형 을
A
′
B
′
C
′
{\displaystyle A'B'C'}
a
′
=
π
−
A
,
b
′
=
π
−
B
,
c
′
=
π
−
C
{\displaystyle a'=\pi -A,\;b'=\pi -B,\;c'=\pi -C}
A
′
=
π
−
a
,
B
′
=
π
−
b
,
C
′
=
π
−
c
{\displaystyle A'=\pi -a,\;B'=\pi -b,\;C'=\pi -c}
따라서 제1 구면 코사인 법칙을 극삼각형
A
′
B
′
C
′
{\displaystyle A'B'C'}
A
B
C
{\displaystyle ABC}
가우스 곡률 -1의 쌍곡면 위의 쌍곡 삼각형
A
B
C
{\displaystyle ABC}
A
,
B
,
C
{\displaystyle A,B,C}
a
,
b
,
c
{\displaystyle a,b,c}
cosh
c
=
cosh
a
cosh
b
−
sinh
a
sinh
b
cos
C
{\displaystyle \cosh c=\cosh a\cosh b-\sinh a\sinh b\cos C}
여기서
cosh
,
sinh
{\displaystyle \cosh ,\sinh }
쌍곡 코사인 , 쌍곡 사인 이다. 이를 (제1) 쌍곡 코사인 법칙 ((第一)雙曲cosine法則, 영어 : (first) hyperbolic law of cosines )이라고 한다. 마찬가지로, 다음이 성립한다.
cos
C
=
−
cos
A
cos
B
+
sin
A
sin
B
cosh
c
{\displaystyle \cos C=-\cos A\cos B+\sin A\sin B\cosh c}
이를 제2 쌍곡 코사인 법칙 (第二雙曲cosine法則, 영어 : second hyperbolic law of cosines )이라고 한다.
이 두 법칙은 각각 다음과 같이 다시 쓸 수 있다.[6] :72
cos
C
=
cosh
a
cosh
b
−
cosh
c
sinh
a
sinh
b
{\displaystyle \cos C={\frac {\cosh a\cosh b-\cosh c}{\sinh a\sinh b}}}
cosh
c
=
cos
A
cos
B
+
cos
C
sin
A
sin
B
{\displaystyle \cosh c={\frac {\cos A\cos B+\cos C}{\sin A\sin B}}}
특히,
C
{\displaystyle C}
쌍곡 피타고라스 정리 가 된다.[6] :72
cosh
c
=
cosh
a
cosh
b
{\displaystyle \cosh c=\cosh a\cosh b}
복소 평면
C
{\displaystyle \mathbb {C} }
열린 단위 원판
D
⊆
C
{\displaystyle D\subseteq \mathbb {C} }
푸앵카레 원판 모형 을 취하자. 쌍곡 삼각형
z
1
,
z
2
,
z
3
{\displaystyle z_{1},z_{2},z_{3}}
A
,
B
,
C
{\displaystyle A,B,C}
a
,
b
,
c
{\displaystyle a,b,c}
D
{\displaystyle D}
등거리 변환 을 가하여
z
3
,
z
2
,
z
1
{\displaystyle z_{3},z_{2},z_{1}}
r
∈
R
+
{\displaystyle r\in \mathbb {R} ^{+}}
허수부
Im
z
>
0
{\displaystyle \operatorname {Im} z>0}
z
{\displaystyle z}
z
,
r
,
0
{\displaystyle z,r,0}
z
1
,
z
2
,
z
3
{\displaystyle z_{1},z_{2},z_{3}}
z
,
r
,
0
{\displaystyle z,r,0}
쌍곡 거리 의 정의에 따라, 세 변은 다음과 같다.
a
=
ln
1
+
r
1
−
r
{\displaystyle a=\ln {\frac {1+r}{1-r}}}
b
=
ln
1
+
|
z
|
1
−
|
z
|
{\displaystyle b=\ln {\frac {1+|z|}{1-|z|}}}
c
=
ln
|
1
−
r
z
|
+
|
z
−
r
|
|
1
−
r
z
|
−
|
z
−
r
|
{\displaystyle c=\ln {\frac {|1-rz|+|z-r|}{|1-rz|-|z-r|}}}
여기서
ln
{\displaystyle \ln }
자연 로그 이며,
|
−
|
{\displaystyle |-|}
절댓값 이다. 이 셋을 다음과 같이 변형할 수 있다.
tanh
a
2
=
r
{\displaystyle \tanh {\frac {a}{2}}=r}
tanh
b
2
=
|
z
|
{\displaystyle \tanh {\frac {b}{2}}=|z|}
tanh
c
2
=
|
z
−
r
|
|
1
−
r
z
|
{\displaystyle \tanh {\frac {c}{2}}={\frac {|z-r|}{|1-rz|}}}
여기서
tanh
{\displaystyle \tanh }
쌍곡 탄젠트 이다. 쌍곡선 함수 의 항등식을 사용한 뒤 위의 결과를 대입하여 정리하면 다음을 얻는다.
cosh
c
=
2
sinh
2
c
2
+
1
=
2
tanh
2
c
2
1
−
tanh
2
c
2
+
1
=
2
|
z
−
r
|
2
|
1
−
r
z
|
2
−
|
z
−
r
|
2
+
1
=
2
r
2
+
|
z
|
2
−
2
r
z
cos
C
(
1
−
r
2
)
(
1
−
|
z
|
2
)
+
1
=
(
1
+
r
2
)
(
1
+
|
z
|
2
)
−
4
r
z
cos
C
(
1
−
r
2
)
(
1
−
|
z
|
2
)
{\displaystyle {\begin{aligned}\cosh c&=2\sinh ^{2}{\frac {c}{2}}+1\\&=2{\frac {\tanh ^{2}{\frac {c}{2}}}{1-\tanh ^{2}{\frac {c}{2}}}}+1\\&=2{\frac {|z-r|^{2}}{|1-rz|^{2}-|z-r|^{2}}}+1\\&=2{\frac {r^{2}+|z|^{2}-2rz\cos C}{(1-r^{2})(1-|z|^{2})}}+1\\&={\frac {(1+r^{2})(1+|z|^{2})-4rz\cos C}{(1-r^{2})(1-|z|^{2})}}\end{aligned}}}
넷째 등호에서 분자 부분은 평면 삼각형
z
,
r
,
0
{\displaystyle z,r,0}
[6] :72-74
cosh
a
=
1
+
tanh
2
a
2
1
−
tanh
2
a
2
=
1
+
r
2
1
−
r
2
{\displaystyle \cosh a={\frac {1+\tanh ^{2}{\frac {a}{2}}}{1-\tanh ^{2}{\frac {a}{2}}}}={\frac {1+r^{2}}{1-r^{2}}}}
sinh
a
=
2
tanh
a
2
1
−
tanh
2
a
2
=
2
r
1
−
r
2
{\displaystyle \sinh a={\frac {2\tanh {\frac {a}{2}}}{1-\tanh ^{2}{\frac {a}{2}}}}={\frac {2r}{1-r^{2}}}}
cosh
b
=
1
+
|
z
|
1
−
|
z
|
{\displaystyle \cosh b={\frac {1+|z|}{1-|z|}}}
sinh
b
=
2
|
z
|
1
−
|
z
|
2
{\displaystyle \sinh b={\frac {2|z|}{1-|z|^{2}}}}
쌍곡 사인 법칙 에 나오는 비율의 구체적인 값은 다음과 같다.
sin
A
sinh
a
=
sin
B
sinh
b
=
sin
C
sinh
c
=
1
−
cosh
2
a
−
cosh
2
b
−
cosh
2
c
+
2
cosh
a
cosh
b
cosh
c
sinh
a
sinh
b
sinh
c
{\displaystyle {\frac {\sin A}{\sinh a}}={\frac {\sin B}{\sinh b}}={\frac {\sin C}{\sinh c}}={\frac {\sqrt {1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}{\sinh a\sinh b\sinh c}}}
이에 따라 각
A
,
B
,
C
{\displaystyle A,B,C}
sin
A
=
1
−
cosh
2
a
−
cosh
2
b
−
cosh
2
c
+
2
cosh
a
cosh
b
cosh
c
sinh
b
sinh
c
{\displaystyle \sin A={\frac {\sqrt {1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}{\sinh b\sinh c}}}
sin
B
=
1
−
cosh
2
a
−
cosh
2
b
−
cosh
2
c
+
2
cosh
a
cosh
b
cosh
c
sinh
a
sinh
c
{\displaystyle \sin B={\frac {\sqrt {1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}{\sinh a\sinh c}}}
sin
C
=
1
−
cosh
2
a
−
cosh
2
b
−
cosh
2
c
+
2
cosh
a
cosh
b
cosh
c
sinh
a
sinh
b
{\displaystyle \sin C={\frac {\sqrt {1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}{\sinh a\sinh b}}}
또한, 제1 쌍곡 코사인 법칙에 따라
A
,
B
,
C
{\displaystyle A,B,C}
cos
A
=
cosh
b
cosh
c
−
cosh
a
sinh
b
sinh
c
{\displaystyle \cos A={\frac {\cosh b\cosh c-\cosh a}{\sinh b\sinh c}}}
cos
B
=
cosh
a
cosh
c
−
cosh
b
sinh
a
sinh
c
{\displaystyle \cos B={\frac {\cosh a\cosh c-\cosh b}{\sinh a\sinh c}}}
cos
C
=
cosh
a
cosh
b
−
cosh
c
sinh
a
sinh
b
{\displaystyle \cos C={\frac {\cosh a\cosh b-\cosh c}{\sinh a\sinh b}}}
따라서, 다음이 성립한다.
cos
A
cos
B
+
cos
C
sin
A
sin
B
=
(
cosh
b
−
cosh
c
−
cosh
a
)
(
cosh
a
cosh
c
−
cosh
b
)
+
sinh
2
c
(
cosh
a
cosh
b
−
cosh
c
)
1
−
cosh
2
a
−
cosh
2
b
−
cosh
2
c
+
2
cosh
a
cosh
b
cosh
c
=
cosh
a
cosh
b
cosh
2
c
−
cosh
2
a
cosh
c
−
cosh
2
b
cosh
c
+
cosh
a
cosh
b
+
cosh
a
cosh
b
sinh
2
c
−
cosh
c
sinh
2
c
1
−
cosh
2
a
−
cosh
2
b
−
cosh
2
c
+
2
cosh
a
cosh
b
cosh
c
=
cosh
c
{\displaystyle {\begin{aligned}{\frac {\cos A\cos B+\cos C}{\sin A\sin B}}&={\frac {(\cosh b-\cosh c-\cosh a)(\cosh a\cosh c-\cosh b)+\sinh ^{2}c(\cosh a\cosh b-\cosh c)}{1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}\\&={\frac {\cosh a\cosh b\cosh ^{2}c-\cosh ^{2}a\cosh c-\cosh ^{2}b\cosh c+\cosh a\cosh b+\cosh a\cosh b\sinh ^{2}c-\cosh c\sinh ^{2}c}{1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}}\\&=\cosh c\end{aligned}}}
마지막 등호에는 항등식
cosh
2
c
−
sinh
2
c
=
1
{\displaystyle \cosh ^{2}c-\sinh ^{2}c=1}
[6] :74-75
평면 코사인 법칙은 제1 구면 및 쌍곡 코사인 법칙의 극한이다. 예를 들어, 평면 코사인 법칙이 제1 쌍곡 코사인 법칙의 극한임을 다음과 같이 보일 수 있다. 푸앵카레 원판의 반지름이
r
{\displaystyle r}
cosh
c
r
r
=
cosh
a
r
r
cosh
b
r
r
−
sinh
a
r
r
sinh
b
r
r
cos
C
r
{\displaystyle \cosh {\frac {c_{r}}{r}}=\cosh {\frac {a_{r}}{r}}\cosh {\frac {b_{r}}{r}}-\sinh {\frac {a_{r}}{r}}\sinh {\frac {b_{r}}{r}}\cos C_{r}}
이 경우,
r
→
∞
{\displaystyle r\to \infty }
a
r
,
b
r
,
c
r
{\displaystyle a_{r},b_{r},c_{r}}
2
a
∞
,
2
b
∞
,
2
c
∞
{\displaystyle 2a_{\infty },2b_{\infty },2c_{\infty }}
A
r
,
B
r
,
C
r
{\displaystyle A_{r},B_{r},C_{r}}
A
∞
,
B
∞
,
C
∞
{\displaystyle A_{\infty },B_{\infty },C_{\infty }}
테일러 정리 에 따라 다음이 성립한다.
cosh
a
r
r
=
1
+
1
2
(
a
r
r
)
2
+
o
(
1
r
2
)
(
r
→
∞
)
{\displaystyle \cosh {\frac {a_{r}}{r}}=1+{\frac {1}{2}}\left({\frac {a_{r}}{r}}\right)^{2}+o\left({\frac {1}{r^{2}}}\right)\qquad (r\to \infty )}
cosh
b
r
r
=
1
+
1
2
(
b
r
r
)
2
+
o
(
1
r
2
)
(
r
→
∞
)
{\displaystyle \cosh {\frac {b_{r}}{r}}=1+{\frac {1}{2}}\left({\frac {b_{r}}{r}}\right)^{2}+o\left({\frac {1}{r^{2}}}\right)\qquad (r\to \infty )}
cosh
c
r
r
=
1
+
1
2
(
c
r
r
)
2
+
o
(
1
r
2
)
(
r
→
∞
)
{\displaystyle \cosh {\frac {c_{r}}{r}}=1+{\frac {1}{2}}\left({\frac {c_{r}}{r}}\right)^{2}+o\left({\frac {1}{r^{2}}}\right)\qquad (r\to \infty )}
이를 법칙에 대입하면 다음을 얻는다.
c
r
2
r
2
=
a
r
2
r
2
+
b
r
2
r
2
−
2
sinh
a
r
r
sinh
b
r
r
cos
C
r
+
o
(
1
r
2
)
(
r
→
∞
)
{\displaystyle {\frac {c_{r}^{2}}{r^{2}}}={\frac {a_{r}^{2}}{r^{2}}}+{\frac {b_{r}^{2}}{r^{2}}}-2\sinh {\frac {a_{r}}{r}}\sinh {\frac {b_{r}}{r}}\cos C_{r}+o\left({\frac {1}{r^{2}}}\right)\qquad (r\to \infty )}
다음에 주의하여, 양변에
r
2
{\displaystyle r^{2}}
r
→
∞
{\displaystyle r\to \infty }
lim
r
→
∞
r
sinh
a
r
r
=
2
a
∞
{\displaystyle \lim _{r\to \infty }r\sinh {\frac {a_{r}}{r}}=2a_{\infty }}
lim
r
→
∞
r
sinh
b
r
r
=
2
b
∞
{\displaystyle \lim _{r\to \infty }r\sinh {\frac {b_{r}}{r}}=2b_{\infty }}
lim
r
→
∞
r
sinh
b
r
r
=
2
c
∞
{\displaystyle \lim _{r\to \infty }r\sinh {\frac {b_{r}}{r}}=2c_{\infty }}
그러면 평면 코사인 법칙을 얻는다.[6] :113-114
c
∞
2
=
a
∞
2
+
b
∞
2
−
2
a
∞
b
∞
cos
C
∞
{\displaystyle c_{\infty }^{2}=a_{\infty }^{2}+b_{\infty }^{2}-2a_{\infty }b_{\infty }\cos C_{\infty }}
제2 쌍곡 코사인 법칙
cos
C
r
=
−
cos
A
r
cos
B
r
+
sin
A
r
sin
B
r
cosh
c
r
r
{\displaystyle \cos C_{r}=-\cos A_{r}\cos B_{r}+\sin A_{r}\sin B_{r}\cosh {\frac {c_{r}}{r}}}
에 극한
r
→
∞
{\displaystyle r\to \infty }
cos
C
∞
=
−
cos
A
∞
cos
B
∞
+
sin
A
∞
sin
B
∞
{\displaystyle \cos C_{\infty }=-\cos A_{\infty }\cos B_{\infty }+\sin A_{\infty }\sin B_{\infty }}
이는
A
∞
+
B
∞
+
C
∞
=
π
{\displaystyle A_{\infty }+B_{\infty }+C_{\infty }=\pi }
[6] :114