지수 함수

지수 함수(指數函數, 영어: exponential function)란 거듭제곱의 지수를 변수로 하고, 정의역을 실수 전체로 정의하는 초월함수이다. 로그 함수의 역함수이다.

지수 함수 ${\displaystyle y=\exp x}$의 그래프

정의

거듭제곱을 통한 정의

지수 함수는 거듭제곱을 사용하여 정의할 수 있다. 먼저 거듭제곱 ${\displaystyle a^{b}}$를 다음과 같이 정의하자.

• ${\displaystyle b}$가 음이 아닌 정수일 때,

  ${\displaystyle a^{b}=\underbrace {a\times \cdots \times a} _{b}}$

• ${\displaystyle b}$가 음의 정수일 때,

  ${\displaystyle a^{b}={\frac {1}{a^{-b}}}}$

• ${\displaystyle b=m/n}$가 유리수이며, ${\displaystyle m}$과 ${\displaystyle n}$이 서로소이며, ${\displaystyle a>0}$일 때,

  ${\displaystyle a^{b}={\sqrt[{n}]{a^{m}}}}$

• ${\displaystyle b}$가 실수이며, ${\displaystyle a>0}$일 때,

  ${\displaystyle a^{b}=\sup _{{\scriptstyle c\in \mathbb {Q} } \atop {\scriptstyle c<b}}a^{c}}$

이제 지수 함수를 정의하자. 1이 아닌 양의 실수

${\displaystyle a>0}$

${\displaystyle a\neq 1}$

를 밑으로 하는 지수 함수 ${\displaystyle f_{a}\colon \mathbb {R} \to \mathbb {R} ^{+}}$는 다음과 같다.

${\displaystyle f_{a}(x)=a^{x}\qquad (x\in \mathbb {R} )}$

여기서 우변은 밑이 ${\displaystyle a}$, 지수가 ${\displaystyle x}$인 거듭제곱이다. 즉, 지수 함수는 밑이 고정된 채 변화하는 지수에 대한 거듭제곱을 구하는 함수이다.

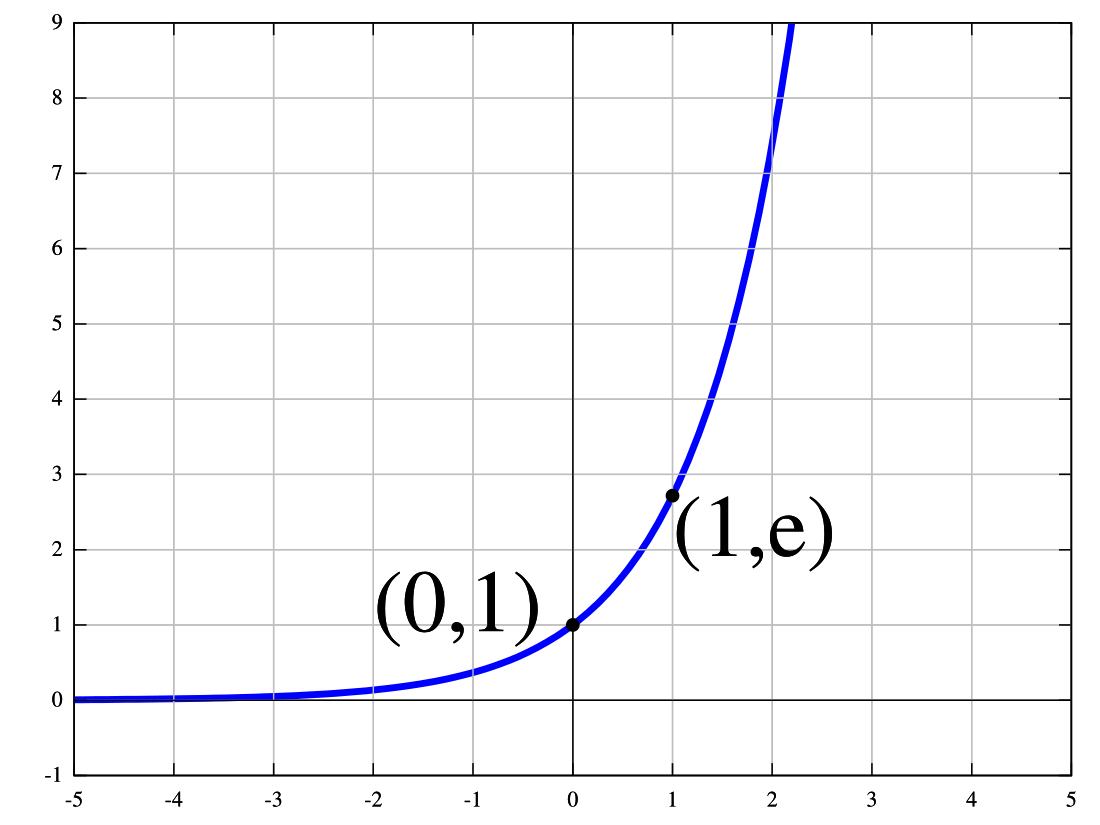
함수

${\displaystyle \exp \colon \mathbb {R} \to \mathbb {R} ^{+}}$

는 자연로그의 밑

${\displaystyle \mathrm {e} =2.71828\cdots }$

을 밑으로 하는 지수 함수

${\displaystyle \exp x=\mathrm {e} ^{x}}$

를 나타낸다. 지수 함수는 흔히 이 특수한 지수 함수만을 일컫는다. 또한, 이를 사용하여 일반적인 밑의 지수 함수를 다음과 같이 나타낼 수 있다.

${\displaystyle a^{x}={\mathrm {e} }^{x\ln a}}$

여기서 ${\displaystyle \ln }$은 자연로그이다. 물론, 다른 특수한 밑부터 시작하여 일반적인 지수 함수에 이를 수도 있다. 하지만 다른 밑에 대한 지수 함수의 직접적인 정의는 상대적으로 더 복잡하다.

극한을 통한 정의

지수 함수 ${\displaystyle \exp \colon \mathbb {R} \to \mathbb {R} ^{+}}$는 다음과 같다.

${\displaystyle \exp x=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}$

우변은 수열의 극한이다. 수열

${\displaystyle \left(1+{\frac {x}{n}}\right)^{n}}$

은 유계 수열이며, ${\displaystyle x>0}$인 경우 순증가, ${\displaystyle x<0}$인 경우 순감소한다. 이는 보통 이항 정리를 사용하여 증명하며, 산술-기하 부등식을 통한 증명도 존재한다. 단조 수렴 정리에 따라, 이 수열은 수렴한다.

일반적인 밑

${\displaystyle a>0}$

${\displaystyle a\neq 1}$

에 대한 지수 함수는 다음과 같다.

${\displaystyle a^{x}=\exp(x\ln a)}$

특히,

${\displaystyle \mathrm {e} ^{x}=\exp(x\ln \mathrm {e} )=\exp x}$

이다.

멱급수를 통한 정의

지수 함수 ${\displaystyle \exp \colon \mathbb {R} \to \mathbb {R} ^{+}}$는 다음과 같다.

${\displaystyle {\begin{aligned}\exp x&=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\\&=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots \end{aligned}}}$

우변은 지수 함수의 테일러 급수이다. 이 급수가 모든 ${\displaystyle x}$에 대하여 수렴함은 이를테면 비 판정법 또는 코시-아다마르 정리를 사용하여 보일 수 있다. 다른 정의를 사용하는 경우, 우변의 멱급수가 테일러 급수임은 이를테면 라그랑주 나머지 항에 대한 테일러 정리를 사용하여 보일 수 있다.

일반적인 밑

${\displaystyle a>0}$

${\displaystyle a\neq 1}$

에 대한 지수 함수는 다음과 같다.

${\displaystyle a^{x}=\exp(x\ln a)}$

특히,

${\displaystyle \mathrm {e} ^{x}=\exp(x\ln \mathrm {e} )=\exp x}$

이다.

로그 함수의 역함수로서의 정의

로그 함수를 정적분을 이용하여 정의할 경우, 지수 함수를 로그 함수의 역함수로 정의할 수 있다.

자연로그를 다음과 같이 정의하자.

${\displaystyle \ln x=\int _{1}^{x}{1 \over t}\,dt}$

이때 ${\displaystyle y=\ln x}$는 강한 증가 함수이며 치역이 실수 전체이므로 역함수가 존재한다. 이때의 역함수를 ${\displaystyle y=\exp(x)}$라고 표기한다.

이 함수의 도함수는 역함수의 미분에 의하여

${\displaystyle {dy \over dx}={1 \over {dx \over dy}}={1 \over {1 \over y}}=y}$

즉, ${\displaystyle {d \over dx}\exp(x)=\exp(x)}$이다. 또한, ${\displaystyle \ln 1=0}$ 이므로, ${\displaystyle \exp(0)=1}$이다.

그리고 로그함수와의 역함수 관계를 이용하여 다음 등식이 성립함을 간단히 보일 수 있다.

${\displaystyle \exp(a+b)=\exp(a)\cdot \exp(b)}$

${\displaystyle \exp(a)=p,\exp(b)=q}$로 놓으면

${\displaystyle a=\ln p,b=\ln q}$이므로 로그의 성질에 의하여 ${\displaystyle a+b=\ln p+\ln q=\ln pq}$

따라서 ${\displaystyle \exp(a+b)=pq=\exp(a)\cdot \exp(b)}$가 성립한다.

로그함수 ${\displaystyle y=\ln x}$는 정의역 전체에서 연속 함수이므로 중간값 정리에 의하여 방정식 ${\displaystyle \ln x=1}$를 만족하는 해 ${\displaystyle x}$가 존재하며, 단사함수이므로 실수 ${\displaystyle x}$는 단 한개만 존재한다. 방정식 ${\displaystyle \ln x=1}$의 해를 ${\displaystyle x=e}$라 하자.

${\displaystyle \therefore \ln e=1,\exp(1)=e}$

이제 ${\displaystyle \exp(x)=e^{x}}$로 놓고 이것을 지수함수로 정의한다.

수학적 귀납법을 이용하면 ${\displaystyle x}$가 자연수일 때 ${\displaystyle \exp(x)=\underbrace {e\times e\times e\times \cdots e} _{x}}$임을 보일 수 있다.

이제 일반적인 밑을 가진 지수를 ${\displaystyle a^{x}=e^{x\ln a}}$ ${\displaystyle (a>0)}$로 정의하자.

마찬가지로 수학적 귀납법을 이용하여 자연수 ${\displaystyle x}$에 대하여 ${\displaystyle a^{x}=\underbrace {a\times a\times a\times \cdots a} _{x}}$임을 보일 수 있다.

증명은 다음과 같다.

1에 대하여 성립

${\displaystyle a^{1}=e^{\ln a}=a}$

${\displaystyle n}$에 대하여 성립한다는 가정 아래, ${\displaystyle n+1}$에 대하여 성립

${\displaystyle a^{n}=\underbrace {a\times a\times a\times \cdots a} _{n}}$

양변에 a를 곱하면

${\displaystyle a^{n}\cdot a=\underbrace {a\times a\times a\times \cdots a} _{n+1}}$

위 식의 좌변은 다음과 같이 정리된다.

${\displaystyle a^{n}\cdot a=a^{n}\cdot a^{1}=e^{n\ln a}\cdot e^{\ln a}=e^{n\ln a+\ln a}=e^{(n+1)\ln a}=a^{n+1}}$

${\displaystyle \therefore a^{n+1}=\underbrace {a\times a\times a\times \cdots a} _{n+1}}$

따라서 수학적 귀납법에 의하여 자연수 ${\displaystyle x}$에 대하여 ${\displaystyle e^{x\ln a}}$로 정의된 ${\displaystyle a^{x}}$는 a를 x번 곱한 것과 같다.

성질

지수 함수의 정의역은 실수 전체이다. 지수 함수의 치역은 양의 실수의 집합 ${\displaystyle \mathbb {R} ^{+}}$이다.

단조성

지수 함수는 단조함수이다. 만약 ${\displaystyle a>1}$이라면, 지수 함수 ${\displaystyle f(x)=a^{x}}$는 증가함수이다. 만약 ${\displaystyle 0<a<1}$이라면, 지수 함수 ${\displaystyle f(x)=a^{x}}$는 감소함수이다.

극한

${\displaystyle a>1}$일 때, 지수 함수의 양과 음의 무한대에서의 극한은 다음과 같다.

${\displaystyle \lim _{x\to \infty }a^{x}=\infty }$

${\displaystyle \lim _{x\to -\infty }a^{x}=0}$

${\displaystyle 0<a<1}$일 때, 지수 함수의 양과 음의 무한대에서의 극한은 다음과 같다.

${\displaystyle \lim _{x\to \infty }a^{x}=0}$

${\displaystyle \lim _{x\to -\infty }a^{x}=\infty }$

따라서, 지수 함수는 ${\displaystyle x}$축을 점근선으로 갖는다.

지수 함수의 유한한 점에서의 극한은 함수의 값과 같다. 즉, 지수 함수는 연속 함수이다.

${\displaystyle \lim _{x\to x_{0}}a^{x}=a^{x_{0}}}$

미분

밑이 자연로그의 밑인 지수 함수 ${\displaystyle \mathrm {e} ^{x}}$의 도함수는 스스로와 같다.

${\displaystyle {\frac {d}{dx}}\mathrm {e} ^{x}=\mathrm {e} ^{x}}$

${\displaystyle a^{x}=\mathrm {e} ^{x\ln a}}$이므로, 일반적인 지수 함수의 도함수는

${\displaystyle {\frac {d}{dx}}a^{x}=a^{x}\ln a}$

가 된다.

연쇄 법칙을 통한 유도:

연쇄 법칙에 따라,

${\displaystyle {\frac {d}{dx}}a^{x}={\frac {d}{dx}}\mathrm {e} ^{x\ln a}={\frac {d\mathrm {e} {x\ln a}}{dx\ln a}}{\frac {dx\ln a}{dx}}=\mathrm {e} {x\ln a}\ln a=a^{x}\ln a}$

음함수 미분을 통한 유도:

${\displaystyle y=a^{x}}$ 양변에 로그를 취하면 다음을 얻는다.

${\displaystyle \ln y=x\ln a}$

양변을 ${\displaystyle x}$에 대하여 미분하면 다음을 얻는다.

${\displaystyle {\frac {1}{y}}{\frac {dy}{dx}}=\ln a}$

정리하면 다음과 같다.

${\displaystyle {\frac {dy}{dx}}=y\ln a=a^{x}\ln a}$

지수 함수 ${\displaystyle y=\mathrm {e} ^{x}}$는 미분 방정식

${\displaystyle dy/dx=y}$

${\displaystyle y(0)=1}$

의 유일한 해이다. 이는 지수 함수의 정의로 삼을 수 있다.

체론적 성질

다음과 같은 유리수 계수 다항식을 생각하자.

${\displaystyle {\begin{aligned}f_{n}(x)&=\sum _{i=0}^{n}x^{i}/i!\\&=((\exp x)/\Gamma (n+1))\int _{x}^{\infty }t^{n}\exp(-t)\,dt\\&\in \mathbb {Q} [x]\end{aligned}}}$

즉, 이는 지수 함수 ${\displaystyle \exp }$의 테일러 급수의 부분합이다. 이 다항식은 유리수 계수 다항식이며, ${\displaystyle n\neq 0}$인 경우 기약 다항식이다. 또한, 이 다항식의 분해체의 갈루아 군은 다음과 같다.^{[1][2][3]:274, Example 8(a)}

${\displaystyle \operatorname {Gal} (f_{n})\cong {\begin{cases}\operatorname {Sym} (n)&4\nmid n\\\operatorname {Alt} (n)&4\mid n\end{cases}}}$

같이 보기

• 자연로그의 밑
• 행렬 지수 함수
• 지수열