고른 다면체

고른 다면체는 정다각형을 면으로 가지고 점추이(그 꼭짓점에서 추이적이다. 즉, 어떤 꼭짓점에서 다른 어떤 꼭짓점으로 등거리 맵핑이 있다)인 다면체이다. 모든 꼭짓점은 합동인 것과 같다.

플라톤의 다면체: 정사면체

고른 별 다면체: 다듬은 십이십이면체

고른 다면체는 (면추이와 변추이일 경우) 정다면체일 수 있고, (변추이이지만 면추이가 아닐 경우) 준정다면체이거나 (변추이도 면추이도 아닌 경우)반정다면체일 수 있다. 면과 꼭짓점은 볼록할 필요는 없어서, 많은 고른 다면체는 별 다면체이다. 다른 75개와 두 가지의 무한한 고른 다면체의 분류가 있다.

• 무한한 분류
  • 각기둥
  • 엇각기둥
• 볼록한 예외
  • 플라톤의 다면체 5개 – 볼록 정다면체
  • 아르키메데스의 다면체 13개 – 볼록 준정다면체 2개와 볼록 반정다면체 11개
• 별다면체 예외
  • 케플러-푸앵소 다면체 4개 – 비볼록 정다면체
  • 고른 별 다면체 53개 – 준정다면체 5개와 반정다면체 48개

존 스킬링(John Skilling)이 발견한 큰 두번다듬은 이중마름모십이면체 (스킬링의 형태)를 포함해서, 모서리의 쌍이 일치하는 많은 불가능한 고른 다면체가 있다.

고른 다면체의 쌍대다면체는 면추이이고 꼭짓점 도형이 정다각형이고, 일반적으로 (고른) 쌍대다면체와 나란하게 분류된다. 정다면체의 쌍대는 정다면체이고, 아르키메데스의 다면체의 쌍대는 카탈랑의 다면체이다.

고른 다면체의 개념은 높은(낮은) 차원의 도형에 적용되는 고른 다포체의 개념의 특별한 경우이다.

정의

The Original Sin in the theory of polyhedra goes back to Euclid, and through Kepler, Poinsot, Cauchy and many others continues to afflict all the work on this topic (including that of the present author). It arises from the fact that the traditional usage of the term “regular polyhedra” was, and is, contrary to syntax and to logic: the words seem to imply that we are dealing, among the objects we call “polyhedra”, with those special ones that deserve to be called “regular”. But at each stage? Euclid, Kepler, Poinsot, Hess, Bruckner,…?the writers failed to define what are the “polyhedra” among which they are finding the “regular” ones.

(Branko Grunbaum 1994)

Coxeter, Longuet-Higgins & Miller (1954)는 고른 다면체를 정다각형 면을 가지는 점추이 다면체로 정의했다. 이들은 다면체를 다각형의 각 변이 다른 다각형의 변의 길이와 같아서 다면체의 적절한 진부분집합이 같은 특성을 가지는 다각형들의 유한집합으로 정의했다. 다각형에 따라서 암묵적으로 3차원 유클리드 공간에 있는 다각형을 의미한다; 이것들은 비볼록하거나 서로 교차하는 것이 가능하다.

고른 다면체의 개념의 일부 일반화가 있다. 만약 연결성 가정이 없어지면, 정육면체 5개의 결합과 같이 다면체 여럿으로 분리될 수 있는 고른 결합체를 얻을 수 있다. 만약 다면체는 불가능하지 않다는 구현화 조건이 없으면, 소위 불가능한 고른 다면체를 얻는다. 이것들은 다면체의 더 일반적인 정의가 필요하다. Grunbaum (1994) harvtxt error: 대상 없음: CITEREFGrunbaum1994 (help)은 다면체에 대한 보다 복잡한 정의를 내었고 McMullen & Schulte (2003) harvtxt error: 대상 없음: CITEREFMcMullenSchulte2003 (help)는 다면체에 대한 더 간단하고 더 일반적인 정의를 주었다: 그들의 용어에서 다면체는 불가능하지 않은 3차원 구현화가 가능한 2차원 추상다포체이다. 여기서 추상다포체는 다양한 조건을 만족하는 그 "면"들의 부분 순서 집합이고, 구현화는 그 꼭짓점을 공간으로 보내는 함수이며, 추상다포체의 어떤 두 구분되는 면이 구분되는 구현화를 가질 경우에 구현화는 불가능하지 않다. 불가능한 경우는 다음과 같다:

• 숨겨진 면. 어떤 다면체는 면이 숨겨져 있다, 즉, 그 면의 내부의 어떤 점도 외부에서 볼 수 없다. 이것들은 보통 고른다면체로 세지 않는다.
• 불가능한 결합체. 어떤 다면체는 다중의 모서리를 가지고 그 면들은 둘 이상의 다면체의 면이지만 이것들은 다면체들이 모서리를 공유하므로 이전 개념의 결합체는 아니다.
• 이중 덮음. 고른 다면체의 정의를 만족하는 이중으로 덮는 비등방성 다면체가 있다. 이것은 그 면과 모서리와 꼭짓점을 두배로 가진다. 이것은 대부분 고른 다면체로 계수하지 않는다.
• 이중 면. 위토프 생성으로 생긴 이중 면을 가지는 다면체가 일부 있다. 대부분의 사람들은 이중 면을 허용하지 않고 생성으로 생긴 것에서 제한다.
• 이중 모서리. 스킬링의 형태는 이중 모서리(불가능한 고른 다면체가 가지는 특성)를 가지지만 그 면들은 고른 다면체 둘의 결합으로 쓰이지는 않는다.

고른 별 다면체

기둥형이 아닌 비볼록 형태 57개는 슈바르츠 삼각형에서 위토프 구성으로 만들어졌다.

 이 부분의 본문은 고른 별 다면체입니다.

별 다면체에 속한다. 별다각형을 밑면으로 하는 각기둥과 엇각기둥을 제외하면 57개가 된다.

볼록다각형

• 팔면반팔면체(Octahemioctahedron)
• 사면반육면체(Tetrahemihexahedron)
• 육면반팔면체(Cubohemioctahedron)
• 큰 십이면체(Great dodecahedron)
• 큰 이십면체(Great icosahedron)
• 큰 이중삼각 이십십이면체(Great ditrigonal icosidodecahedron)
• 작은 마름모육면체(Small rhombihexahedron)
• 작은 육육팔면체(Small cubicuboctahedron)
• 비볼록 큰 마름모육팔면체(Nonconvex great rhombicuboctahedron)
• 작은 십이면반십이면체(Small dodecahemidodecahedron)
• 큰 십이면반이십면체(Great dodecahemicosahedron)
• 작은 이십면반십이면체(Small icosihemidodecahedron)
• 작은 십이이십면체(Small dodecicosahedron)
• 작은 마름모십이면체(Small rhombidodecahedron)
• 작은 십이이십십이면체(Small dodecicosidodecahedron)
• 마름모이십면체(Rhombicosahedron)
• 큰 이십이십십이면체(Great icosicosidodecahedron)

오목 다각형

• 작은 별모양 십이면체(Small stellated dodecahedron)
• 큰 별모양 십이면체(Great stellated dodecahedron)
• 이중삼각 십이십이면체(Ditrigonal dodecadodecahedron)
• 작은 이중삼각 이십십이면체(Small ditrigonal icosidodecahedron)
• 별모양 깎은 육면체(Stellated truncated hexahedron)
• 큰 마름모육면체(Great rhombihexahedron)
• 큰 육육팔면체(Great cubicuboctahedron)
• 큰 십이면반십이면체(Great dodecahemidodecahedron)
• 작은 십이면반이십면체(Small dodecahemicosahedron)
• 십이십이면체(Dodecadodecahedron)
• 큰 이십면반십이면체(Great icosihemidodecahedron)
• 큰 이십십이면체(Great icosidodecahedron)
• 육면체깎은 육팔면체(Cubitruncated cuboctahedron)
• 큰 깎은 육팔면체(Great truncated cuboctahedron)
• 깎은 큰 십이면체(Truncated great dodecahedron)
• 작은 별모양 깎은 십이면체(Small stellated truncated dodecahedron)
• 큰 별모양 깎은 십이면체(Great stellated truncated dodecahedron)
• 깎은 큰 이십면체(Truncated great icosahedron)
• 큰 십이이십면체(Great dodecicosahedron)
• 큰 마름모십이면체(Great rhombidodecahedron)
• 이십십이십이면체(Icosidodecadodecahedron)
• 작은 이중삼각 십이이십십이면체(Small ditrigonal dodecicosidodecahedron)
• 큰 이중삼각 십이이십십이면체(Great ditrigonal dodecicosidodecahedron)
• 큰 십이이십십이면체(Great dodecicosidodecahedron)
• 작은 이십이십십이면체(Small icosicosidodecahedron)
• 마름모십이십이면체(Rhombidodecadodecahedron)
• 비볼록 큰 마름모이십십이면체(Nonconvex great rhombicosidodecahedron)
• 다듬은 십이십이면체(Snub dodecadodecahedron)
• 뒤집어 다듬은 십이십이면체(Inverted snub dodecadodecahedron)
• 큰 다듬은 이십십이면체(Great snub icosidodecahedron)
• 큰 뒤집어 다듬은 이십십이면체(Great inverted snub icosidodecahedron)
• 큰 거꾸로다듬은 이십십이면체(Great retrosnub icosidodecahedron)
• 큰 다듬은 십이이십십이면체(Great snub dodecicosidodecahedron)
• 다듬은 이십십이십이면체(Snub icosidodecadodecahedron)
• 작은 다듬은 이십이십십이면체(Small snub icosicosidodecahedron)
• 작은 거꾸로다듬은 이십이십십이면체(Small retrosnub icosicosidodecahedron)
• 큰 이중마름모이십십이면체(Great dirhombicosidodecahedron)
• 이십면체깎은 십이십이면체(Icositruncated dodecadodecahedron)
• 깎은 십이십이면체(Truncated dodecadodecahedron)
• 큰 깎은 이십십이면체(Great truncated icosidodecahedron)

John Skilling의 다면체

한 모서리가 세 면이상에 속할 수 있는 다면체이다.

• 큰 두번다듬은 이중마름모십이면체(Great disnub dirhombidodecahedron)

위토프 구성의 볼록한 형태

정육면체와 정팔면체에서 만들어진 예

볼록한 고른 다면체는 위토프 생성 연산자와 원래 형태간의 관계를 통해 이름을 지을 수 있다.

졸록한 고른 다면체의 세부사항은 아래에 각 대칭군에서 위토프 구성으로 주어졌다.

위토프 생성에서, 낮은 대칭 형태에서 만들어진 것과 중복되는 것이 있다. 정육면체는 정다면체이면서 사각기둥이다. 정팔면체는 정다면체이자 고른엇각기둥이며 사각쌍뿔이다. 많은 다면체는 다른 생성 방법에서 중복되며 다르게 색칠된다.

위토프 생성은 고른 다면체와 구면위의 고른 타일링에 동일하게 적용하므로 그림은 둘 다 주어졌다. 구면 타일링은 호소헤드론과 이면체와 같은 불가능한 다면체를 포함한다.

이 대칭군은 삼차원의 점군의 대칭으로 생성되고, 각각은 기본 삼각형 (p q r)로 나타난다. 이 때, p > 1, q > 1, r > 1 이고 1/p + 1/q + 1/r < 1이다.

정다면체 대칭군은 이면체를 제외하고 다음의 3가지가 있다. 또한 종류거 무수히 많은 각기둥과 엇각기둥, 그리고 이면체와 호소헤드론을 제외하면 고른 다면체는 모두 28가지이다. 이중에서 반정다면채는 20개이고, 준정다면체를 재외하면 17개이다. 자세한 내용은 해당 문서를 참조할 것

• 정사면체 대칭 (3 3 2) – 24 차
• 정팔면체 대칭 (4 3 2) – 48 차
• 정이십면체 대칭 (5 3 2) – 120 차
• 이면체 대칭 n = 3,4,5,... 일 때, (n 2 2) – 4n 차

나머지 비반사 형태는 변이 짝수개인 다각형으로 덮인 다면체에 교대 연산을 적용해서 생성된다.

각기둥과 그 이면체 대칭을 따라, 구면 위토프 생성은 불가능한 정다면체 두 그룹을 만든다 – 이면체와 호소헤드론이다. 이면체는 면이 둘 뿐이고, 호소헤드론은 꼭짓점이 둘 뿐이다. 깎은 정호소헤드론은 각기둥을 만든다.

아래의 기둥형이 아닌 볼록한 고른 다면체는 대칭 형태의 표에서 1–18까지 색인되어있다.

기둥형의 무한한 집합에 대해서는 네 족만을 색인해놓았다:

1. 호소헤드론 H_2... (구면 타일링에서만 가능)
2. 이면체 D_2... (구면 타일링에서만 가능)
3. 각기둥 P_3... (깎은 호소헤드론)
4. 엇각기둥 A_3... (다듬은 각기둥)

나머지 비반사 형태들은 짝수개의 변을 가지는 면으로 이루어진 다면체에 교대 연산자를 적용하여 생성된다.

각기둥과 그 이면체 대칭을 따라, 구면 위토프 생성 과정은 불가능한 정다면체의 두 분류를 만든다 – 이면체와 호소헤드론이다. 이면체는 면이 둘 뿐이고, 호소헤드론은 꼭짓점이 둘 뿐이다. 호소헤드론을 깎으면 각기둥이 생간다.

아래의 볼록한 고른 다면체는 각기둥이 아닌 형태에 대해서 대칭 형태의 표에 1-18까지 색인하여 나타냈다.

기둥 형태의 무한집합에 대해서는 네 족으로 색인을 했다:

1. 호소헤드론 H_2... (구면 타일링에서만 가능)
2. 이면체 D_2... (구면 타일링에서만 가능)
3. 각기둥 P_3... (깎은 호소헤드론)
4. 엇각기둥 A_3... (다듬은 각기둥)

요약 표

존슨 이름	원본	깎기	절반 깎기	비트 깎기 (깎은 쌍대)	완전 깎기 (쌍대)	부풀림	부풀려 깎기	다듬음
콕서터 다이어그램
확장된 슐레플리 기호	${\displaystyle {\begin{Bmatrix}p,q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p,q\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}q,p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}q,p\end{Bmatrix}}}$	${\displaystyle r{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p\\q\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}p\\q\end{Bmatrix}}}$
	{p,q}	t{p,q}	r{p,q}	2t{p,q}	2r{p,q}	rr{p,q}	tr{p,q}	sr{p,q}
	t0{p,q}	t0,1{p,q}	t1{p,q}	t1,2{p,q}	t2{p,q}	t0,2{p,q}	t0,1,2{p,q}	ht0,1,2{p,q}
위토프 기호 (p q 2)	q | p 2	2 q | p	2 | p q	2 p | q	p | q 2	p q | 2	p q 2 |	| p q 2
꼭짓점 도형	pq	q.2p.2p	(p.q)2	p.2q.2q	qp	p.4.q.4	4.2p.2q	3.3.p.3.q
정사면체 (3 3 2)	3.3.3	3.6.6	3.3.3.3	3.6.6	3.3.3	3.4.3.4	4.6.6	3.3.3.3.3
정팔면체 (4 3 2)	4.4.4	3.8.8	3.4.3.4	4.6.6	3.3.3.3	3.4.4.4	4.6.8	3.3.3.3.4
정이십면체 (5 3 2)	5.5.5	3.10.10	3.5.3.5	5.6.6	3.3.3.3.3	3.4.5.4	4.6.10	3.3.3.3.5

그리고 이면체 대칭의 표본이다:

(p 2 2)	원본	깎기	절반 깎기	비트 깎기 (깎은 쌍대)	완전 깎기 (쌍대)	부풀림	부풀려 깎기	다듬음
콕서터 다이어그램
확장된 슐레플리 기호	${\displaystyle {\begin{Bmatrix}p,2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p,2\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}p\\2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}2,p\end{Bmatrix}}}$	${\displaystyle {\begin{Bmatrix}2,p\end{Bmatrix}}}$	${\displaystyle r{\begin{Bmatrix}p\\2\end{Bmatrix}}}$	${\displaystyle t{\begin{Bmatrix}p\\2\end{Bmatrix}}}$	${\displaystyle s{\begin{Bmatrix}p\\2\end{Bmatrix}}}$
	{p,2}	t{p,2}	r{p,2}	2t{p,2}	2r{p,2}	rr{p,2}	tr{p,2}	sr{p,2}
	t0{p,2}	t0,1{p,2}	t1{p,2}	t1,2{p,2}	t2{p,2}	t0,2{p,2}	t0,1,2{p,2}	ht0,1,2{p,2}
위토프 기호	2 | p 2	2 2 | p	2 | p 2	2 p | 2	p | 2 2	p 2 | 2	p 2 2 |	| p 2 2
꼭짓점 도형	p2	2.2p.2p	p.2.p.2	p.4.4	2p	p.4.2.4	4.2p.4	3.3.3.p
이면체 대칭 (2 2 2)	{2,2}	2.4.4	2.2.2.2	4.4.2	2.2	2.4.2.4	4.4.4	3.3.3.2
이면체 대칭 (3 2 2)	3.3	2.6.6	2.3.2.3	4.4.3	2.2.2	2.4.3.4	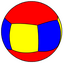4.4.6	3.3.3.3
이면체 대칭 (4 2 2)	4.4	2.8.8	2.4.2.4	4.4.4	2.2.2.2	2.4.4.4	4.4.8	3.3.3.4
이면체 대칭 (5 2 2)	5.5	2.10.10	2.5.2.5	4.4.5	2.2.2.2.2	2.4.5.4	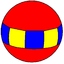4.4.10	3.3.3.5
이면체 대칭 (6 2 2)	6.6	2.12.12	2.6.2.6	4.4.6	2.2.2.2.2.2	2.4.6.4	4.4.12	3.3.3.6

(3 3 2) T_d 정사면체 대칭

구면에서 정사면체 대칭은 고른 다면체 5개를 만들고, 다듬음 연산자를 통해 여섯번째 형태를 만든다.

정사면체 대칭은 한 꼭짓점은 거울이 두 개 있고, 다른 두 꼭짓점은 거울이 세 개 있는 기본 삼각형 (3 3 2)로 나타난다. 이것은 콕서터 군 A₂또는 [3,3]과 콕서터 다이어그램 으로도 나타낼 수 있다.

삼각형이 24개가 있으며, 삼방육면체의 면에서, 구면에 교대로 색칠해서 나타냈다:

#	이름	그래프 A3	그래프 A2	그림	타일링	꼭짓점 도형	콕서터와 슐레플리 기호	위치에 있는 면			원소 수
								Pos. 2 [3] (4)	Pos. 1 [2] (6)	Pos. 0 [3] (4)	면	선	꼭짓점
1	정사면체						{3,3}	{3}			4	6	4
[1]	완전 깎은 정사면체 (정사면체와 같음)						t2{3,3}={3,3}			{3}	4	6	4
2	절반 깍은 정사면체 (정팔면체와 같음)						t1{3,3}=r{3,3}	{3}		{3}	8	12	6
3	깎은 정사면체						t0,1{3,3}=t{3,3}	{6}		{3}	8	18	12
[3]	비트 깎은 정사면체 (깎은 정사면체)						t1,2{3,3}=t{3,3}	{3}		{6}	8	18	12
4	마름모사사각형 (육팔면체와 같음)						t0,2{3,3}=rr{3,3}	{3}	{4}	{3}	14	24	12
5	깎은 사사면체 (깎은 정팔면체와 같음)						t0,1,2{3,3}=tr{3,3}	{6}	{4}	{6}	14	36	24
6	다듬은 사사면체 (정이십면체와 같음)		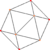				sr{3,3}	{3}	2 {3}	{3}	20	30	12

(4 3 2) O_h 정팔면체 대칭

구면에서 정팔면체 대칭은 고른 다면체 7개를 만들고, 교대 연산을 하면 7개 더 만든다. 이 형태중 여섯 개는 위에 있는 정사면체 대칭 표의 내용과 중복된다.

정팔면체 대칭은 꼭짓점에 있는 거울 개수로 (4 3 2)인 기본 삼각형으로 나타난다. 콕서터 군으로 B₂또는 [4,3]과 콕서터 다이어그램 으로 표시할 수 있다.

삼각형이 48개가 있으며, 육방팔면체의 면과 구면에 교대로 색칠해서 나타냈다:

#	이름	그래프 B3	그래프 B2	그림	타일링	꼭짓점 도형	콕서터와 슐레플리 기호	위치에 있는 면			원소 수
								Pos. 2 [4] (6)	Pos. 1 [2] (12)	Pos. 0 [3] (8)	면	모서리	꼭짓점
7	정육면체						{4,3}	{4}			6	12	8
[2]	정팔면체						{3,4}			{3}	8	12	6
[4]	절반 깎은 정육면체 절반 깎은 정팔면체 (육팔면체)						{4,3}	{4}		{3}	14	24	12
8	깎은 정육면체						t0,1{4,3}=t{4,3}	{8}		{3}	14	36	24
[5]	깎은 정팔면체						t0,1{3,4}=t{3,4}	{4}		{6}	14	36	24
9	부풀린 정육면체 부풀린 정팔면체 마름모육팔면체						t0,2{4,3}=rr{4,3}	{8}	{4}	{6}	26	48	24
10	부풀려 깎은 정육면체 부풀려 깎은 정팔면체 깎은 육팔면체						t0,1,2{4,3}=tr{4,3}	{8}	{4}	{6}	26	72	48
[6]	다듬은 정팔면체 (정이십면체와 같음)						= s{3,4}=sr{3,3}		{3}	{3}	20	30	12
[1]	절반 정육면체 (정사면체와 같음)						= h{4,3}={3,3}	1/2 {3}			4	6	4
[2]	Cantic 정육면체 (깎은 정사면체)						= h2{4,3}=t{3,3}	1/2 {6}		1/2 {3}	8	18	12
[4]	(육팔면체와 같음)						= rr{3,3}				14	24	12
[5]	(깎은 정팔면체와 같음)						= tr{3,3}				14	36	24
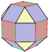
[9]	Cantic 깎은 정팔면체 (마름모육팔면체)						s2{3,4}=rr{3,4}				26	48	24
11	다듬은 육팔면체						sr{4,3}	{4}	2 {3}	{3}	38	60	24

(5 3 2) I_h 정이십면체 대칭

구면에서 정이십면체 대칭은 고른 다면체 7개를 만들고, 교대 연산을 통해 하나를 더 만든다. 하나만이 위의 정사면체나 정팔면체 대칭 표와 중복된다.

정이십면체 대칭은 꼭짓점에 있는 거울의 개수로 (5 3 2)인 기본 삼각형으로 나타낼 수 있다. 콕서터 군으로 G₂이나 [5,3]과 콕서터 다이어그램 으로 나타낼 수 있다.

삼각형이 120개가 있으며, 육방이십면체의 면과 구면에서 교대로 색칠해서 나타냈다:

#	이름	그래프 (A2) [6]	그래프 (H3) [10]	그림	타일링	꼭짓점 도형	콕서터와 슐레플리 기호	위치에 있는 면			원소 수
								Pos. 2 [5] (12)	Pos. 1 [2] (30)	Pos. 0 [3] (20)	면	모서리	꼭짓점
12	정십이면체						{5,3}	{5}			12	30	20
[6]	정이십면체						{3,5}			{3}	20	30	12
13	절반 깎은 정십이면체 절반 깎은 정이십면체 십이이십면체						t1{5,3}=r{5,3}	{5}		{3}	32	60	30
14	깎은 정십이면체						t0,1{5,3}=t{5,3}	{10}		{3}	32	90	60
15	깎은 정이십면체		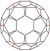				t0,1{3,5}=t{3,5}	{5}		{6}	32	90	60
16	부풀린 정십이면체 부풀인 정이십면체 마름모십이이십면체						t0,2{5,3}=rr{5,3}	{5}	{4}	{3}	62	120	60
17	부풀려 깎은 정십이면체 부풀려 깎은 정이십면체 깎은 십이이십면체						t0,1,2{5,3}=tr{5,3}	{10}	{4}	{6}	62	180	120
18	다듬은 십이이십면체						sr{5,3}	{5}	2 {3}	{3}	92	150	60

(p 2 2) 기둥형 [p,2], I₂(p) 족(D_ph 이면체 대칭)

 이 부분의 본문은 기둥형 고른 다면체입니다.

구면에서 이면체 대칭은 두 종류의 무한 고른 다면체 집합(각기둥과 엇각기둥)을 만들고, 구면에서 타일링으로만 존재하는 불가능한 두 종류의 다면체 그룹, 호소헤드론과 이면체를 만든다.

정이십면체 대칭은 꼭짓점에 있는 거울의 개수로 (p 2 2)인 기본 삼각형으로 나타낼 수 있다. 콕서터 군으로 I₂(p)이나 [n,2]와 기둥형의 콕서터 다이어그램 으로 나타낼 수 있다.

아래에는 D₂ ... D₆까지 처음 다섯가지 이면체 대칭을 나타냈다. 이면체 대칭 D_p는 4n차이고, 쌍각뿔의 면과 구의 적도와 n개의 등간격의 경도로 나타난다.

(2 2 2) 이면체 대칭

기본 삼각형은 8개가 있으며, 사각쌍뿔(정팔면체)의 면과 구면에서 교대로 색칠해서 나타냈다:

#	이름	그림	타일링	꼭짓점 도형	콕서터와 슐레플리 기호	위치에 있는 면			원소 수
						Pos. 2 [2] (2)	Pos. 1 [2] (2)	Pos. 0 [2] (2)	면	모서리	꼭짓점
D2 H2	이각형 이면체 이각 호소헤드론				{2,2}	{2}			2	2	2
D4	깎은 이각형 이면체 (사각형 이면체와 같다)				t{2,2}={4,2}	{4}			2	4	4
P4 [7]	부풀려 깍은 이각형 이면체 (정육면체와 같다)				t0,1,2{2,2}=tr{2,2}	{4}	{4}	{4}	6	12	8
A2 [1]	다듬은 이각형 이면체 (정사면체와 같다)				sr{2,2}		2 {3}		4	6	4

(3 2 2) D_3h 이면체 대칭

기본 삼각형은 12개가 있으며, 육각쌍뿔의 면과 구면에서 교대로 색칠해서 나타냈다:

#	이름	그림	타일링	꼭짓점 도형	콕서터와 슐레플리 기호	위치에 있는 면			원소 수
						Pos. 2 [3] (2)	Pos. 1 [2] (3)	Pos. 0 [2] (3)	면	모서리	꼭짓점
D3	삼각형 이면체				{3,2}	{3}			2	3	3
H3	삼각 호소헤드론				{2,3}			{2}	3	3	2
D6	깎은 삼각형 이면체 (육각형 이면체와 같다)				t{3,2}	{6}			2	6	6
P3	깎은 삼각 호소헤드론 (삼각기둥과 같다)				t{2,3}	{3}	{4}		5	9	6
P6	부풀려 깎은 삼각형 이면체 (육각기둥)				t0,1,2{2,3}=tr{2,3}	{6}	{4}	{4}	8	18	12
A3 [2]	다듬은 삼각형 이면체 (고른엇각기둥) (정팔면체와 같다)				sr{2,3}	{3}	2 {3}		8	12	6
P3	Cantic 다듬은 삼각형 이면체 (삼각기둥)				s2{2,3}=t{2,3}				5	9	6

(4 2 2) D_4h 이면체 대칭

기본 삼각형은 16개가 있으며, 팔각쌍뿔의 면으로 나타냈다:

#	이름	그림	타일링	꼭짓점 도형	콕서터와 슐레플리 기호	위치에 있는 면			원소 수
						Pos. 2 [4] (2)	Pos. 1 [2] (4)	Pos. 0 [2] (4)	면	모서리	꼭짓점
D4	사각형 이면체				{4,2}	{4}			2	4	4
H4	사각 호소헤드론				{2,4}			{2}	4	4	2
D8	깎은 사각형 이면체 (팔각 이면체와 같다)				t{4,2}	{8}			2	8	8
P4 [7]	깎은 사각 호소헤드론 (정육면체와 같다)				t{2,4}	{4}	{4}		6	12	8
D8	부풀려 깎은 사각형 이면체 (팔각기둥과 같다)				t0,1,2{2,4}=tr{2,4}	{8}	{4}	{4}	10	24	16
A4	다듬은 사각형 이면체 (엇사각기둥과 같다)				sr{2,4}	{4}	2 {3}		10	16	8
P4 [7]	Cantic 다듬은 사각형 이면체 (정육면체와 같다)				s2{4,2}=t{2,4}				6	12	8
A2 [1]	다듬은 사각 호소헤드론 (엇이각기둥) (정사면체)				s{2,4}=sr{2,2}				4	6	4

(5 2 2) D_5h 이면체 대칭

기본 삼각형은 20개가 있으며, 십각쌍뿔면에서 나타냈다:

#	이름	그림	타일링	꼭짓점 도형	콕서터와 슐레플리 기호	위치에 있는 면			원소 수
						Pos. 2 [5] (2)	Pos. 1 [2] (5)	Pos. 0 [2] (5)	면	모서리	꼭짓점
D5	오각형 이면체				{5,2}	{5}			2	5	5
H5	오각 호소헤드론				{2,5}			{2}	5	5	2
D10	깎은 오각형 이면체 (십각 이면체와 같다)				t{5,2}	{10}			2	10	10
P5	깎은 오각 호소헤드론 (오각기둥과 같다)				t{2,5}	{5}	{4}		7	15	10
P10	부풀려 깎은 오각형 이면체 (삽각기둥과 같다)				t0,1,2{2,5}=tr{2,5}	{10}	{4}	{4}	12	30	20
A5	다듬은 오각형 이면체 (엇오각기둥)				sr{2,5}	{5}	2 {3}		12	20	10
P5	Cantic 다듬은 오각형 이면체 (오각기둥)				s2{5,2}=t{2,5}				7	15	10

(6 2 2) D_6h 이면체 대칭

기본 삼각형은 24개가 있다.

#	이름	그림	타일링	꼭짓점 도형	콕서터와 슐레플리 기호	위치에 있는 면			원소 수
						Pos. 2 [6] (2)	Pos. 1 [2] (6)	Pos. 0 [2] (6)	면	모서리	꼭짓점
D6	육각형 이면체				{6,2}	{6}			2	6	6
H6	육각 호소헤드론				{2,6}			{2}	6	6	2
D12	깎은 육각형 이면체 (십이각형 이면체와 같다)				t{6,2}	{12}			2	12	12
H6	깎은 육각 호소헤드론 (육각기둥과 같다)				t{2,6}	{6}	{4}		8	18	12
P12	부풀려 깎은 육각형 이면체 (십이각기둥과 같다)				t0,1,2{2,6}=tr{2,6}	{12}	{4}	{4}	14	36	24
A6	다듬은 육각형 이면체 (엇육각기둥과 같다)				sr{2,6}	{6}	2 {3}		14	24	12
P3	Cantic 육각형 이면체 (삼각기둥과 같다)				= h2{6,2}=t{2,3}				5	9	6
P6	Cantic 다듬은 육각형 이면체 (육각기둥과 같다)				s2{6,2}=t{2,6}				8	18	12
A3 [2]	다듬은 육각 호소헤드론 (엇고른엇각기둥각기둥과 같다) (정팔면체와 같다)				s{2,6}=sr{2,3}				8	12	6

같이 보기

• 다면체
  • 정다면체
  • 준정다면체
  • 반정다면체
• 고른 다면체의 목록
• 존슨의 다면체의 목록
• 웨닝거 다면체 모델의 목록
• 다면체 모델
• 꼭짓점 도형에 의한 고른 다면체 목록
• 위토프 기호에 의한 고른 다면체 목록
• 슈바르츠 삼각형에 의한 고른 다면체 목록
• 고른 타일링
• 쌍곡면의 고른 타일링

참고 자료

• Brückner, M. Vielecke und vielflache. Theorie und geschichte.. Leipzig, Germany: Teubner, 1900.
• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). “Uniform polyhedra” (PDF). 《Philosophical Transactions of the Royal Society A》 (왕립학회) 246 (916): 401–450. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446.
• B., Grünbaum (1994), 〈Polyhedra with Hollow Faces〉, Tibor Bisztriczky; Peter McMullen; Rolf Schneider; 외., 《Proceedings of the NATO Advanced Study Institute on Polytopes: Abstract, Convex and Computational》, Springer, 43–70쪽, ISBN 978-94-010-4398-4
• Sopov, S. P. (1970). “A proof of the completeness on the list of elementary homogeneous polyhedra”. 《Ukrainskiui Geometricheskiui Sbornik》 (8): 139–156. MR 0326550.
• Wenninger, Magnus (1974). 《Polyhedron Models》. Cambridge University Press. ISBN 0-521-09859-9.
• Skilling, J. (1975). “The complete set of uniform polyhedra”. 《Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences》 278 (1278): 111–135. doi:10.1098/rsta.1975.0022. ISSN 0080-4614. JSTOR 74475. MR 0365333.

외부 링크

• Weisstein, Eric Wolfgang. “Uniform Polyhedron”. 《Wolfram MathWorld》 (영어). Wolfram Research.
• Uniform Solution for Uniform Polyhedra
• The Uniform Polyhedra
• Virtual Polyhedra Uniform Polyhedra
• Uniform polyhedron gallery Archived 2016년 10월 9일 - 웨이백 머신
• Uniform Polyhedron -- from Wolfram MathWorld Has a visual chart of all 75