モスクワ数学パピルス (モスクワすうがくパピルス、Moscow Mathematical Papyrus)は、古代エジプト の数学文書。エジプト学者ウラジーミル・セミョーノヴィチ・ゴレニシチェフ(Владимир Семёнович Голенищев , Vladimir Goleniščev )が1893年 にエジプト からロシア に持ち帰った。もとはテーベ (現・ルクソール )付近のネクロポリス 、ドゥラ・アブ・アル=ナーガ(Dra Abu el-Naga)にあった[1] ゴレニシチェフ数学パピルス (Golenischev Mathematical Papyrus)とも呼ばれる。その後1911年 にモスクワ のプーシキン美術館 に他の古代エジプト文物とともに寄贈され、今もそこにある。4676番という所蔵番号からモスクワ4676パピルスとも呼ばれる[2]
モスクワ数学パピルスの14番目の問題 ヒエラティック で書かれた古文書 であり、エジプト第11王朝 時代のものとされている。長さ約5m50cm、幅は4cmから7.5cmで、ソビエト連邦 の東洋学 者ヴァシーリー・ヴァシーリエヴィチ・シュトルーヴェ(Vasily Vasilievich Struve [3] [4] リンド数学パピルス と共に古代エジプトの数学文書として有名である。モスクワ数学パピルスの方が古いが、リンド数学パピルスの方が大きい[5]
モスクワ数学パピルスの第10問題は、半球 の表面積を問う問題である。曲面の面積の近似値を求める問題としては最も古い問題の1つである。
次のような例が書かれている。「かご(半球)の(表面積の)計算例。半球の開口部(の直径)は 4 + 1/2(の比率)。表面は? かごは卵形の半分(半球)なので、9の1/9を求める。すなわち1が得られる。(9から引いて)残りを計算すると8。8の1/9を計算する。2/3 + 1/6 + 1/18 が得られる。8からこれを引いた残りを求める。2/3 + 1/6 + 1/18 を引くと 7 + 1/9 が得られる。7 + 1/9 と 4 + 1/2 をかけると32が得られる。これが表面(積)である」[6]
この計算を式に表すと次のようになる(d は直径)。
A
=
2
×
d
×
8
9
×
8
9
×
d
=
128
81
d
2
{\displaystyle A=2\times d\times {\frac {8}{9}}\times {\frac {8}{9}}\times d={\frac {128}{81}}d^{2}}
一方、正しい半球面の表面積 は次のようになる。
A
=
1
2
π
d
2
{\displaystyle A={\frac {1}{2}}\pi d^{2}}
以上から、古代エジプト人は円周率 の近似値として、次の値を使っていたことがわかる。
π
≈
256
81
=
3
+
1
9
+
1
27
+
1
81
≈
3.1605....
{\displaystyle \pi \approx {\frac {256}{81}}=3+{\frac {1}{9}}+{\frac {1}{27}}+{\frac {1}{81}}\approx 3.1605....}
モスクワ数学パピルスの第14問題は、その中でも最も難問で、切頭体 の体積を求める問題である。切頭体の体積を求める最古の例の1つである。古代の数学で完全な多角錐や円錐の体積を求める例は知られていない[7] メソポタミア でも同様に、完全な角錐や円錐よりも切頭体の体積を求めることに興味を持っていたと思われる。例えばバビロニア の数学粘土板 BM 85194 には、城塞の壁の一部である台形状の部分の体積を求める計算が刻まれている。
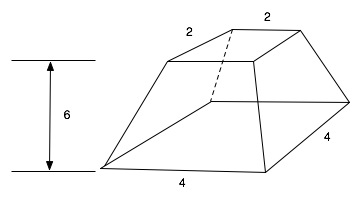
第14問題では、上面が1辺の長さ2の正方形で、底面が1辺の長さ4の正方形、高さが6の正四角錐台の体積を求めている。その解は56と記されていて、正しい解である。
解法は次のように書かれている。「正四角錐台は高さが6、底面の辺が4、上面の辺が2である。4を2乗して16となる。4を2倍して8となる。2を2乗して4となる。16と8と4を足して28を得る。6の1/3を求め2を得る。28を2倍して56を得る。この56が正しい解である」[8]
式で表すと次のようになり、正しい式である。
V
=
1
3
6
(
4
2
+
4
×
2
+
2
2
)
{\displaystyle V={\frac {1}{3}}6(4^{2}+4\times 2+2^{2})}
すなわち、古代エジプト人は正四角錐台の正しい体積 の公式を知っていたとわかる。高さを h 、底面の辺を a 、上面の辺を b とすると、次のような公式となる。
V
=
1
3
h
(
a
2
+
a
b
+
b
2
)
.
{\displaystyle V={\frac {1}{3}}h(a^{2}+ab+b^{2}).}
古代エジプト人がどのようにして正しい公式にたどり着いたのかは不明である。バビロニア人は、上面と底面の面積の平均をとり、それに高さをかけるという間違った計算法を採用していた[9]
不思議なことにモスクワ数学パピルスに最初に注釈をつけた Touraeff は、この第14問題が任意の切頭体の体積を与える公式を示していると考えた[10] A は底面の面積、B は上面の面積)。このような見方をするのは Touraeff だけではない[11]
V
=
1
3
h
(
A
+
A
B
+
B
)
.
{\displaystyle V={\frac {1}{3}}h(A+{\sqrt {AB}}+B).}
正四角錐台の体積を正しく求めていることから、これを積分法 の起源とする見方もある[12] [13]
Heinz-Wilhelm Alten: 4000 Jahre Algebra , Heidelberg, Springer, 2003. Seite 12
Struve, Vasilij Vasil'evič, and Boris Turaev. 1930. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau . Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer
as given in Gunn & Peet, Journal of Egyptian Archaeology, 1929, 15: 176. See also, Van der Waerden, 1961, Plate 5
see the examples in BM 85194, BM 85196, BM 85210, as given in O. Neugebauer, Mathematische Keilschrift-Texte, Volume 1, 1935, chapter 3, and F. Thureau-Dangin, Textes Mathematiques Babyloniens, 1938, chapter 1
B. A. Touraeff, "The Volume of the Truncated Pyramid in Egyptian Mathematics", Ancient Egypt , 1917, pages 100 – 102
Solomon Gandz echoed Touraeff in Quellen u. Studien z. Geschichte der Mathematik 1932, A, 2: 1– 96.
Morris Kline, Mathematical thought from ancient to modern times , Vol. I
モスクワ数学パピルス全文 Struve, Vasilij Vasil'evič, and Boris Turaev. 1930. Mathematischer Papyrus des Staatlichen Museums der Schönen Künste in Moskau . Quellen und Studien zur Geschichte der Mathematik; Abteilung A: Quellen 1. Berlin: J. Springer その他 Allen, Don. April 2001. The Moscow Papyrus Summary of Egyptian Mathematics
Clagett, Marshall. 1999. Ancient Egyptian Science: A Source Book. Volume 3: Ancient Egyptian Mathematics . Memoirs of the American Philosophical Society 232. Philadelphia: American Philosophical Society. ISBN 0-87169-232-5
Couchoud, Sylvia .Gardner, Milo,
Imhausen, A., Ägyptische Algorithmen. Eine Untersuchung zu den mittelägyptischen mathematischen Aufgabentexten, Wiesbaden 2003.
Mathpages.com. The Prismoidal Formula
O'Connor and Robertson, 2000. Mathematics in Egyptian Papyri
Truman State University, Math and Computer Science Division. Mathematics and the Liberal Arts: Ancient Egypt The Moscow Mathematical Papyrus
Williams, Scott W. Mathematicians of the African Diaspora Egyptian Mathematics Papyri
Zahrt, Kim R. W. Thoughts on Ancient Egyptian Mathematics