音の大きさ

音の大きさ（おとのおおきさ、（英: loudness）はヒトが聴覚で感じる音の大小を示す心理量である^[1]。ラウドネスとも。

概要

音の大きさはヒトが聴覚で感じる音の知覚的大小を示す心理量である^[1][2]（⇒ #定義）。単位はソーンであり（⇒ #単位）、主観評価実験により測定される（⇒ #測定）。その値は耳に届いた音波の物理的特性に大きく左右される（⇒ #音波との関係）。より簡便に値を推定するため音圧を補正した様々な心理物理量が提案されており（⇒ #推定）、この推定モデルが様々な場面で応用されている（⇒ #応用）。また統一的な扱いのために音の大きさとその推定に関する標準規格が定められている（⇒ #標準規格）。

音の大きさは音の高さ、音色と合わせて、音の知覚的属性である「音の3属性」を構成する^[3]。

定義

JIS Z8106:2000 では音の大きさ（ラウドネス）を次のように定義する^[4]：

音の大きさ，ラウドネス
聴覚にかかわる音の属性の一つで，小から大に至る尺度上に配列される。 — JIS Z 8106:2000

ISO 532-1:2017 では音の大きさ（ラウドネス）を次のように定義する^[2]：

loudness
perceived magnitude of a sound, which depends on the acoustic properties of the sound and the specific listening conditions, as estimated by otologically normal persons — ISO 532-1:2017

単位

ソーン（英: sone）は音の大きさの単位である^[5]。ソンとも^[5]。

音圧レベル40[dB]・周波数1,000[Hz]の純音をヒトが聴いた際に感じる音の大きさが1 soneと定義される^[5]。1 soneから、ヒトの感じる音の大きさが2倍になれば2 sone、半分になれば0.5 sone、無音であれば 0 soneとなる^[5][6]。

測定

音の大きさは心理量であるため、個々人が感じた音の大きさを聞き取ることで測定される。

ソーンの定義により 1 sone となる音源が用意できるため^[5]、これを基準値として「基準音の何倍に聞こえるか」を尋ねる主観評価実験で音の大きさの絶対値を測定できる。またリファレンス音と対象音を聴き比べ「どちらが大きく聞こえるか」を尋ねる主観評価実験を用いれば相対的な音の大きさの大小を測定できる。

音波との関係

音の大きさは耳へ到達した音波の物理的特性によって左右される^[7][8]。

音の強さの影響

音の大きさは音の強さに影響される^[9]。

周波数の影響

→「周波数マスキング」も参照

音の大きさは音の周波数と周波数スペクトル構造に影響される^[10][11][12]。

等ラウドネス曲線

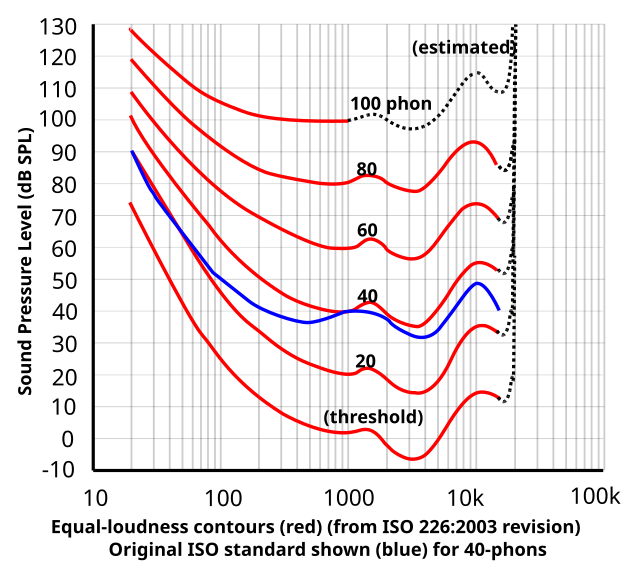
ヒトの聴覚は音波の周波数によって感度が異なる^[13]。つまり2つの純音が同じ音の強さであっても周波数が異なれば音の大きさが異なる^[11][14]。音の大きさが一定となる純音の音圧レベルを各周波数で示したグラフは等ラウドネス曲線として知られ^[15][14]、ここからヒトが 4kHz 周辺の純音に最も鋭敏であることがわかる^[13][16]（図参照）。等ラウドネス曲線の測定は古くから測定が繰り返されており、フレッチャー=マンソンによるものが著名であるが、近年では、鈴木と竹島によるものがISO 226:2003として規格化されている^[14][16]。

また同時に近しい周波数の音波が耳に届いた場合、片方が他方をマスクし音の大きさに影響する場合がある^[12]。すなわち各時刻の周波数スペクトル構造が音の大きさに影響しうる。この現象を周波数マスキングという。

時間構造の影響

→詳細は「経時マスキング § 聴覚の継時マスキング」を参照

音の大きさは音の時間構造に影響される。

推定

音の大きさはしばしば直接計測でなく心理物理量を介した推定によって測られる。

心理量の計測は高コストであり、しばしば代替として心理物理量を介した推定がなされる^[17]。音の大きさもこれに該当し、様々な推定モデルが提案されている。モデルごとに精度や適用可能条件が異なり^[18]、必要に応じて使い分けられる。周波数で補正した音圧を用いるモデルや周波数マスキングを考慮したモデルが存在する^[19][20]（例: 騒音レベル（A特性音圧レベル）、Moore-Glasberg法^[21]）。

ラウドネスレベル

等ラウドネス曲線。横軸は周波数、縦軸は音圧レベル。ラウドネスレベルのフォン[phon]と音圧レベルを表すデシベル[dB]との関係を示す。

→「ホン § ラウドネスレベル」も参照

ラウドネスレベル （あるいは音の大きさのレベル 英: loudness level）は、ある音の大きさについて、同じ大きさ（ラウドネス）に聞こえる周波数1,000ヘルツ[Hz]の純音の音圧レベル（単位:デシベル[dB]）で表した心理物理量である。単位はフォン[phon]^[22]。

ヒトの聴覚は音の周波数によって感度が異なり^[13]、これは等ラウドネス曲線で表現される^[15]（⇒ #周波数の影響）。周波数に依存しない音圧レベル（物理量）を周波数に依存する音の大きさ（心理量）に対応させるため、ラウドネスレベル（心理物理量）では音圧レベルを等ラウドネス曲線で補正する^[19]。この曲線において、周波数1000ヘルツ[Hz]の純音のラウドネスレベル（フォン[phon]）の値は、その音圧レベル（単位:デシベル[dB]）の値に等しく、これ以外の周波数では、同じラウドネスに聞こえる1000ヘルツの純音の音圧レベルに等しい^[22]。したがって、同じフォンの音は同じ音の大きさに聞こえると期待される^[23]。

等ラウドネス曲線は等間隔でないため、同じ周波数で音圧レベルが1デシベル増えてもラウドネスレベルが1フォン増えるとは限らず、後述の騒音レベルとは異なり、ラウドネスレベルのフォン値のみが判明している2つの音について、それらの音を合成したラウドネスレベルの値を算定することはできない。

純音の主観評価実験に基づく等ラウドネス曲線に依拠するタイプのラウドネスレベルを複合音計測に適用すると、ラウドネスとの関係は一般には保たれない。周波数マスキングはその原因の1つである^[12]（⇒ #周波数の影響）。

なお、ラウドネスとラウドネスレベルの尺度関係は明確でない。フォンとソーンには「フォン[phon] ÷ 10 - 4 = log₂ソーン[sone]」の関係があるという知見に基づき、比率尺度として${\displaystyle sone\sim k*phon^{0.3}}$、すなわち10[phon]で2倍のラウドネスが得られる（等比）という研究^[24]、間隔尺度として10[dB]で騒音カテゴリが1つあがる（等差）という研究が存在する^[25]。

算定ラウドネスレベル

等ラウドネス曲線などにより音声信号から計算して求めたラウドネスレベルをJISでは算定ラウドネスレベルという。単位は同じくフォン （phon）である。計算方法はISO 532に示されている^[26][27]。例えば ${\displaystyle f}$ [Hz] の純音に関して、補正係数を ${\displaystyle w_{f}}$、計測された音圧レベルを ${\displaystyle L}$ [dB_SPL]とすると、この純音のラウドネスレベルは ${\displaystyle w_{f}\times L}$ [phon] である。^[要出典]

騒音レベル（A特性音圧レベル）

→「A特性」および「ホン § 騒音レベル」も参照

周波数による聴感補正グラフ
平坦特性をZ特性といい、A,C特性は等ラウドネス曲線のそれぞれ60,100 phonに近似した重みづけである。その中間のB特性と、航空機騒音評価のために提案されたD特性は音源の改善により用いられなくなった^[28]。

さまざまな周波数により構成される音の大きさの評価について、周波数による感覚的な音の大きさの違いを踏まえて、周波数による聴感補正を行った音圧を用いる。通常用いられるサウンドレベルメータ（騒音計）には、このような周波数による聴感補正を行う周波数補正回路が、音の大きさのレベルを近似的に測定する目的で挿入されている^[29]。

騒音の測定に用いる聴感補正は、A特性によるものが一般的である。A特性は、フレッチャー=マンソンの40 phonにおける等ラウドネスレベル曲線を逆にしたものに近似される。このA特性により周波数重みづけを行った音圧p_Aを用いて算定した音圧レベル（A特性音圧レベル）L_Aを、騒音レベルといい、騒音の大きさの評価に用いられる^[30]。

応用

音量調整

音響機器・オーディオソフトウェアが発する音声信号の音量調整/volume control（音量正規化）にラウドネスは用いられる。

異なる2つの楽曲の音量について、最大振幅において出力される音圧のパワーレベルが同じになるように制御しても、ラウドネスは音圧のみによらず周波数成分などにも左右されるため、それぞれの楽曲のピークレベルの音に対して聞き手が感じる音の大きさ（ラウドネス）が一致しない場合がある。聞き手のラウドネスを一致させたいのであれば、機材側での音量調整段階でラウドネスを揃えればよい。すなわちラウドネスレベル等の聴感補正が行われた値を用いて、複数の音声信号間でラウドネスを均一化することをラウドネス正規化（英語版）という。

標準規格

音の大きさに関する様々な標準規格が提案されている。以下はその一例である：

表. 音の大きさに関する標準規格

番号	名称
Published
ISO 226:2023	Acoustics — Normal equal-loudness-level contours
ISO 532-1:2017	Acoustics — Methods for calculating loudness — Part 1: Zwicker method
ISO 532-2:2017	Acoustics — Methods for calculating loudness — Part 2: Moore-Glasberg method
JIS Z 8106:2000	音響用語
Withdrawn
ISO 226:2003	Acoustics — Normal equal-loudness-level contours
ISO 226:1987	Acoustics — Normal equal-loudness level contours
ISO 532:1975	Acoustics — Method for calculating loudness level
ISO/R 226:1961	Normal equal-loudness contours for pure tones and normal threshold of hearing under free field listening conditions