球面調和関数
ウィキペディアから
球面調和関数(きゅうめんちょうわかんすう、英: spherical harmonics[1])あるいは球関数(きゅうかんすう、英: spherical functions[2])は以下のいずれかを意味する関数である:
- n 次元ラプラス方程式の解となる斉次多項式を単位球面に制限する事で得られる関数。
- 次元 n が 3 の場合の 1 の意味での球面調和関数で、球面座標 (r, θ, φ) で書いたラプラス方程式の変数分離解を記述するのに用いる事ができる関数 Y n
k (θ, φ).


本項では 1 及び 2 双方の意味の球面調和関数について述べるが、特に断りがない限り、「球面調和関数」という言葉を 1 の意味で用いる。
定義
要約
視点
R を実数全体の集合とし、C を複素数全体の集合とし、n 個の実数からなる組の集合を Rn とし、Rn の元を (x1, …, xn) ∈ Rn と書き表すことにする。
Rn 上の複素数値関数
- φ: Rn → C
が2階微分可能なとき、Δφ を
と定義し、Δ をラプラス作用素という。さらに Rn 上の(複素数値の)多項式 p(x1, …, xn) で
- Δp = 0
を満たすものを調和多項式という[3]。なおラプラス作用素は回転行列 R に対し、
- Δp(R(x)) = R(Δp(x))
を満たすので[4]、調和多項式の定義は座標系のとり方に依存しない。
調和多項式 p が k 次の斉次多項式であるとき、p を単位球面
(P1)
に制限した制限写像
を k 次の球面調和関数という[5]。
(n 次元空間 Rn における)k 次の球面調和関数全体の集合を Hk とすると、Hk は C 上のベクトル空間であり、
(P2)
である[6]。
帯球関数
要約
視点
en を Rn 上のベクトル
- en = (0, ..., 0, 1) ∈ Rn
とする。
定義 (帯球関数) ― 以下の性質を満たす k 次の球面調和関数を、(en 方向の)k 次の帯球関数という[7]:
- R(en) = en を満たす任意の回転行列 R に対し、Y(R(x1, …, xn)) = Y(x1, …, xn)
次元 n が 3 であれば、z 軸 (0, 0, 1) を保つ回転によって球面 S2 を回せば、球面上に緯線が帯状に描かれる。帯球関数という名称は、「緯線による帯上で値が不変になる球面調和関数」である事に由来する[7]。
次の事実が成立する[7]。
定理 ― 任意の自然数 k に対し、Rn 上の k 次の帯球関数は定数倍を除いて一意である。すなわち Z1, Z2 を Rn 上の2つの k 次帯球関数とするとき、Z1 = aZ2 を満たす複素数 a ∈ C が存在する。
具体的表記
帯球関数を具体的に書き表す為、記号を導入する。自然数 n と非負の実数 x に対しポッホハマー記号 (x)n を
により定義する。ここで Γ(x) はガンマ関数である。さらにガウスの超幾何関数を
により定義する[注 2]。このとき、次が成立する。
- は k 次の帯球関数である[8]。
すでに述べたように、k 次の帯球関数は定数倍を除いて一意なので、全ての k 次帯球関数は上述したものの定数倍として表記可能である。
3次元空間における球面調和関数
要約
視点
3次元空間 R3 の場合、R3 を球面座標 (r, θ, φ) で表すと、下記の Y m
k (θ, φ) が球面調和関数になる事が知られている。
(B1)
ここで
m は整数で、k ≥ |m|
(B2)
であり、P m
k (t) はルジャンドルの陪多項式[9]
(B3)
である。すなわち P m
k (t) はルジャンドルの陪微分方程式
の解である。なお、ルジャンドルの陪微分方程式は条件 (B2) を満たすとき、およびそのときだけ解を持つことが知られている。また、Y m
k (θ, φ) の定義における係数は、後述するノルムが1になるよう選んだものである。
Y m
k (θ, φ) が球面調和関数の定義を満たすことは自明ではないが、p を p(r, θ, φ) = rk Y m
k (θ, φ) と定義した上で直交座標に変換すると p が斉次多項式になっている事を確認できる。
なお、本項では、「球面調和関数」という言葉をラプラス方程式の解となる斉次多項式(の球面への制限)一般を指す用語として用いるが、物理の教科書などでは上述した Y m
k (θ, φ) のみを球面調和関数と呼んでいるものも多い。
Ykm(θ, φ) の意義
Y m
k (θ, φ) は斉次多項式に関する3次元空間のラプラス方程式を変数分離で解く事で自然に得られる。k 次の斉次多項式 p に対し、変数分離形
- p(r, θ, φ) = R(r) Θ(θ) Φ(φ)
でラプラス方程式 Δp = 0 を解くと、変数分離形の解は必ず
- m は整数で k ≤ |m|
と書ける事を証明できる。
証明
Y m
k (θ, φ) は斉次多項式に関する3次元空間のラプラス方程式を変数分離で解く事で自然に得られるものである。このことを見るために3次元空間 R3 を球面座標 (r, θ, φ) でラプラス作用素を表記すると、
となる。ここで、
である。定義より次数 k の球面調和関数は、k 次の斉次多項式 p を単位球面上に制限したものとして表現可能である。p が k 次の斉次多項式である事から、p の極座標表示は
p(r, θ, φ) = rkY(θ, φ)
(A1)
の形に書ける。ラプラス方程式 Δp = 0 の以下、変数分離解
- Y(θ, φ) = Θ(θ) Φ(φ)
を求める。R(r) = rk とすれば、
なので、変数分離解をラプラス方程式の極座標表示に代入することで、
が成立する。上式に対してさらに変数分離を適用する事で、複素数 m を適切に選べば
(A2)
(A3)
が成立する事がわかる。以下、m が定数である場合の解を求める。
(A2) は初等的に解くことができ、一般解
(A4)
を得られる。ここで i は虚数単位である。それに対しスツルム=リウヴィル型の微分方程式 (A3) は t = cos θ と変数変換すると、y(t) = Θ(arccos t) はルジャンドルの陪微分方程式
を満たす。よってルジャンドルの陪多項式 P m
k (t) を (B3) のように定義すれば、結論として
(A5)
がわかる。ここで k は (B2) の条件を満たす整数である。そこで Y m
k (θ, φ) を
と定義すれば、(A1), (A4), (A5), (B2) より、変数分離形の k 次の調和多項式 p は必ず
- m は整数で k ≤ |m|,
と書ける事になる。なお、p を直交座標に変換すると p が斉次多項式になっている事を確認できる。
また、3次元空間の場合、k 次球面調和関数全体のなすベクトル空間 Hk の次元は、(P2) より
なので、(B2) より、以下の結論が得られる:
定理1 ― 3次元空間の場合、Y −k
k (θ, φ), …, Y k
k (θ, φ) は Hk の基底である。すなわち3次元空間の場合、(変数分離形とは限らない)次数 k の斉次多項式(の球面への制限)Y が球面調和関数となる必要十分条件は、Y がこれらの関数の線形和として書ける事である。
球面上の完全直交性
要約
視点
本節では、球面調和関数の空間に内積を定義し、球面調和関数がこの内積に関して完全直交性を満たすことを示す。
球面調和関数に対する内積
n 次元空間 Rn の単位球面 Sn − 1 を (P1) のように定義し、dS を Sn−1 上の面素とし、Sn − 1 上定義された2つの球面調和関数 f, g の内積を
(C1)
により定義する。なお、面素 dS は球面座標 (r, θ1, …, θn − 1) を
を用いて
と書ける[10]。特に 3 次元空間の場合は球面座標 (r, θ, φ) に対し、
である。
直交性
k 次球面調和関数全体のなすベクトル空間を Hk とすると、以上のように定義された内積に対し、以下の事実が成立する事が知られている。
定理 ― 2つの非負整数 k ≠ j に対し、Hk と Hj は (C1) で定義された内積に関して直交する。すなわち任意の f ∈ Hk, g ∈ Hj に対し、⟨f|g⟩Sn−1 = 0 が成立する[11]。
特に 3 次元空間では次が成立する。
定理 ―
完全直交性
Hk が更に強い性質を満たすことも証明可能である。Sn − 1 上の自乗可積分函数全体の空間
- L2(Sn − 1) = { f: Sn − 1 → C | f は可測かつ ⟨ f | f ⟩Sn − 1 が有限値 }
は Hk を使って直交分解可能である[11]:
定理 ― (ヒルベルト直和)。
これを言い換えると、以下の系が従う:
特に 3 次元の場合は、上述の事実と定理1から以下が成立する:
定理 ― 任意の f ∈ L2(Sn − 1) に対し、f を極座標で表したとき、
を満たす複素数の族 {Ak, m}k = 0, 1, …; m = −k, …, k で
となるものが一意に存在する。
3次元空間における完全直交性
要約
視点
3 次元空間 R3 の球面座標 (r, θ, φ) に対し、
が成立する。そこで、R 上の関数 χ, ξ に対し、χ, ξ の内積を
(D1)
により定義し、さらに R3 の関数 f1, f2 の内積を
(D2)
とする。f1, f2 が
- f1(x) = χ1(r) Y1(θ, φ), f2(x) = χ2(r) Y2(θ, φ)
と変数分離形で書けていた場合には、(C1), (D1), (D2) で定義した内積は以下の性質を満たす。
(C1), (D1), (D2) の内積を用いて自乗可積分な関数全体の集合をそれぞれ L2(S2, sin θ dθ dφ), L2(R, r2 dr), L2(R3, dx dy dz) と書くと、ヒルベルト空間の一般論から、次が成立する[注 3]。
定理 ― 次が成立する:
- (ヒルベルトテンソル積)。
上述した定理と定理1から、以下の結論が従う。
系 ― R3 上の任意の自乗可積分関数 f(x, y, z) に対し、⟨χk, m|χk, m⟩R < ∞ を満たす R 上の可積分関数の族 {χk, m(r)} で
となるものが一意に存在する。
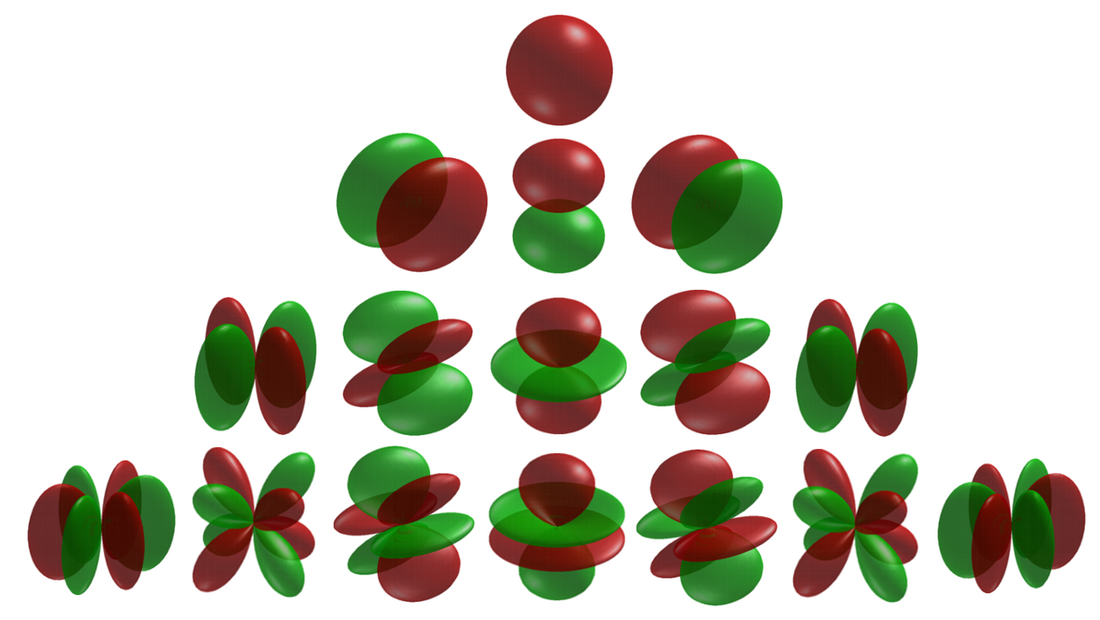
Ykm(θ, φ) の具体例
要約
視点
→詳細は「球面調和関数表」を参照
いくつかの球面調和関数の具体的な表式を示す。
代数的性質
要約
視点
加法定理
球面調和関数には「加法定理」と呼ばれる性質がある。これは三角関数における加法定理
を一般化したものと捉えることができる。上式の右辺は球面調和関数に、左辺はルジャンドル多項式に置き換えられる。
二つの単位ベクトル x および y を考え、それらの球面座標をそれぞれ (θ, φ) および (θ′, φ′) とする。このとき、加法定理は以下のように表すことができる[12]:
(1)
ここで Pℓ は ℓ 次のルジャンドル多項式である。この表式は実数調和関数・虚数調和関数の双方について成り立つ[注 4]。この結果は単位球面上のポアソン核の性質を用いて、あるいはベクトル y を z 軸に沿うように幾何的に回転させたのちに右辺を直接計算することにより解析的に証明することができる[13]。
特に、x = y の場合はウンゼルトの定理[14]
に帰着する。この式は一次元の三角関数における恒等式 cos2 θ + sin2θ = 1 を二次元に拡張したものとみなすことができる。
式 (1) の左辺 Pℓ(x⋅y) は ℓ 次の帯球調和関数の定数倍である。この観点から、より高次元の場合にも次のように一般化することができる。Yj を n 次元超球面上の ℓ 次の球面調和関数の張る空間 Hℓ の任意の正規直交基底とする。このとき、単位ベクトル x に対応する ℓ 次の帯球調和関数 Z (ℓ)
x は以下のように書き下せる[15]。
(2)
さらに、帯球調和関数 Z (ℓ)
x (y) は適切なゲーゲンバウアー多項式の定数倍として表すことができる:
(3)
x および y が球面座標で表される場合、(2) および (3) を組み合わせると (1) が得られる。最後に、x = y の場合を評価すると次の恒等式が得られる:
ここで ωn − 1 は (n − 1) 次元超球の体積である。
クレブシュ–ゴルダン係数
クレブシュ–ゴルダン係数とは、二つの球面調和関数の積を球面調和関数の線形結合で展開する際の展開係数である。ウィグナーの3-j記号やラカー係数、スレーター積分など様々な計算方法があるが、本質は同じである。抽象的には、クレブシュ–ゴルダン係数は二つの回転群の既約表現のテンソル積を既約表現の和で表わすときの係数と見ることができる。よって、適切に正規化すれば多重度と一致する。
パリティ
原点に対する点対称操作で符号が替わらない(偶関数)かあるいは符号が逆になる(奇関数)かに依って、球面調和関数に対する「パリティ」が定義される。原点を不動点とする点対称操作は PΨ(r→) = Ψ(−r→) と表わせる。立体角で表わせば、{θ, φ} を {π − θ, π + φ} に置き換える操作になる。ルジャンドル陪多項式(Associated Legendre polynomials)はパリティとして (−1)ℓ + m を、指数関数は (−1)m を与えるので、両者を併せると球面調和関数のパリティは(mには依らずに) (−1)ℓ となる。
このことは、高次元に一般化した場合にも成り立つ。ℓ 次の球面調和関数に点対称操作を施した場合、符号の変化は (−1)ℓ となる。 (これは調和多項式が次数の偶・奇に併せて空間反転で偶関数・奇関数であること、球面調和函数が調和多項式の球面上への制限であることからも容易に理解できる。)
量子力学での応用
要約
視点
量子力学で、球対称なポテンシャル V(r) に対する1粒子シュレーディンガー方程式(代表的なものは水素原子のシュレーディンガー方程式)
を解いたときに、球面調和関数が現れる。量子力学では Y m
ℓ の ℓ, m を量子数と呼び、それぞれ ℓ を方位量子数、m を磁気量子数という。
球面調和関数は軌道角運動量 ℓ と密接な関係がある。球面調和関数は ℓ2 と ℓz の同時固有関数になっており、その固有値はそれぞれ ħ2ℓ(ℓ + 1), mħ である。すなわち
となる。また、上昇下降演算子 ℓ+, ℓ− を球面調和関数に作用させると
となる。
脚注
文献
関連項目
外部リンク
Wikiwand - on
Seamless Wikipedia browsing. On steroids.










![{\displaystyle (1-t^{2})y''(t)-2t\,y'(t)+\left[k(k+1)-{\frac {m^{2}}{1-t^{2}}}\right]y(t)=0}](http://wikimedia.org/api/rest_v1/media/math/render/svg/e95eb38f855a0934ae78930f2c29765f5ab21260)









































