ヤコビの楕円関数

数学において、ヤコビの楕円関数（ヤコビのだえんかんすう、英: Jacobi elliptic functions）とは、基本的な楕円関数の一群であり、追加でテータ関数を含むこともあり、歴史的に重要な関数からなる。これらの関数は重要な構造を持っていて、さらに直接関連した応用も存在する。三角関数との類似性も便利で、sin に対応する関数を sn と表記する^[2]。実用的な問題にはヴァイエルシュトラスの楕円函数よりもヤコビの楕円関数のほうがよく用いられる。これは複素解析の概念を使わずに定義し考察できるからである。これらの関数はCarl Gustav Jakob Jacobi (1829)により導入された。

導入

説明用の長方形

ヤコビの楕円関数は全部で12種類ある。これら12種は長方形のある頂点から他の頂点へ引いた矢印に対応している。ここでは、この頂点を順に s、c、d、n と呼ぶことにする。この長方形を複素平面に配置して、s は原点に、c は実軸上の K の位置に、d は K + iK' の位置に、n は虚軸上の iK' の位置になるようにする。実数 K と K' は四半周期（英語版）と呼ばれる。このとき、 s、c、d、n から異なる2文字を選んで「p」と「q」とすると、ヤコビの楕円関数は「pq」と書くことができる。

ヤコビの楕円関数は二重周期を持つ有理型関数で、次の性質を満たす唯一のものをいう。

• 頂点 p に一位の零点を持ち、頂点 q には一位の極を持つ
• p から q までが関数 pq u の半周期となる。つまり、関数 pq u は pq の向きの周期を持っており、その周期は p と q の距離の倍である。さらに、関数 pq u はほかの2方向についても周期的であり、p から残りの頂点への距離が 1/4 周期である。
• 関数 pq u を各頂点で u について展開すると、先頭の項の係数は 1 となる。言い換えると、関数 pq u を、頂点 p において展開した場合の先頭の項は u であり、頂点 q では 1/u であり、残りの頂点では 1 である。

より一般的には、長方形である必要はなく、平行四辺形でもよい。しかし、K と iK' をそれぞれ実軸と虚軸に置いておくと、ヤコビの楕円関数 pq u は、u が実数のとき実数値を取る。

記法

楕円関数には様々な記法があり、無用な混乱を引き起こしている。楕円関数は2変数の関数である。最初の変数は振幅φを使って表すこともあるが、一般には、以下のように u を使う。二番目の変数はパラメタ m を使ったり、母数（英語版） k を使って表す。ここで、k² = m である。他にも、modular angle（英語版） α を使うこともある。m =  sin² α である。これら別記法の定義や発展した話題、相補的な対応概念については、楕円積分や四半周期（英語版）の記事を見られたい。

楕円積分の逆関数による定義

k = 0.8 の場合のヤコビの楕円関数 sn。domain coloring法で生成^[3]。

上記のように、特定の性質を持つ唯一の有理型関数として定義するのは非常に抽象的である。より単純で、完全に同値な定義として、第1種不完全楕円積分の逆関数として定義することができる。まず、

${\displaystyle u=\int _{0}^{\phi }{\frac {\mathrm {d} \theta }{\sqrt {1-m\sin ^{2}\theta }}}}$

とする。楕円関数 sn u は

${\displaystyle \operatorname {sn} \;u=\sin \phi \,}$

で与えられ、cn u は

${\displaystyle \operatorname {cn} \;u=\cos \phi }$

で与えられ、dn u は

${\displaystyle \operatorname {dn} \;u={\sqrt {1-m\sin ^{2}\phi }}}$

で与えられる。

uとkを独立に動かしたときの振幅の模型(垂直軸が振幅)

ここで、角 ${\displaystyle \phi }$ を振幅と呼ぶ。dn u = Δ(u) をdelta amplitudeと呼ぶこともある。上の値 m は自由なパラメタで、通常は実数を使い、0 ≤ m ≤ 1 とする。これにより、楕円関数は、ふたつの変数、振幅${\displaystyle \phi }$とパラメタmの関数だと考えることができる。

残りの9つの楕円関数は上記の3つから簡単に構成することができ、下の節で与えられる。

注意として、${\displaystyle \phi =\pi /2}$ の場合は、u は四半周期 K となる。

三角法による定義

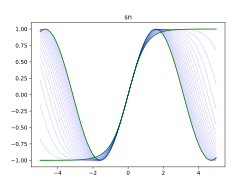
sn(u, m) のグラフは m → 0 のとき sin(u) 、m → 1 のとき tanh(u) へ漸近する。

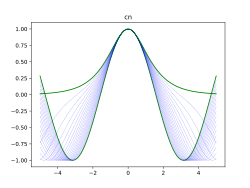
cn(u, m) のグラフは m → 0 のとき cos(u) 、m → 1 のとき sech(u) へ漸近する。

dn(u, m) のグラフは m → 0 のとき 1 、m → 1 のとき sech(u) へ漸近する。

r = 1 の単位円上で${\displaystyle \cos \theta ,\sin \theta }$を定義できたのと同様に、ヤコビの楕円関数は、a = 1 の単位楕円上で定義できる。

${\displaystyle {\begin{aligned}&x^{2}+{\frac {y^{2}}{b^{2}}}=1,\quad b>1,\\&m=1-{\frac {1}{b^{2}}},\quad 0<m<1,\\&x=r\cos \theta ,\quad y=r\sin \theta \end{aligned}}}$

とすると、

${\displaystyle r(\theta ,m)={\frac {1}{\sqrt {1-m\sin ^{2}\theta }}}}$

である。

楕円に沿った弧長 u を計算すると、

${\displaystyle u=u(\varphi ,m)=\int _{0}^{\varphi }r(\theta ,m)\,d\theta }$

となる。ここで、${\displaystyle \varphi =\arccos(x)}$である。単位円でおなじみの関係式

${\displaystyle \cos \theta =x,\quad \sin \theta =y}$

を楕円の場合に一般化して、

${\displaystyle \operatorname {cn} (u,m)=x,\quad \operatorname {sn} (u,m)={\frac {y}{b}}}$

を定義とする。

さらに、

${\displaystyle \operatorname {dn} (u,m)={\frac {1}{r(\varphi ,m)}}}$

と定める。

テータ関数を用いた定義

ヤコビによるテータ関数を用いて定義することもできる。${\displaystyle \vartheta (0;\tau )}$を${\displaystyle \vartheta }$と略記し、${\displaystyle \vartheta _{01}(0;\tau ),\vartheta _{10}(0;\tau ),\vartheta _{11}(0;\tau )}$もそれぞれ、${\displaystyle \vartheta _{01},\vartheta _{10},\vartheta _{11}}$(テータ定数と呼ばれる)と略記する。このとき、母数 k は${\displaystyle k=\left({\vartheta _{10} \over \vartheta }\right)^{2}}$ となる。${\displaystyle u=\pi \vartheta ^{2}z}$とおくと、

Elliptic Jacobi function, cn, k = 0.8

Elliptic Jacobi function, dn, k = 0.8

${\displaystyle \mathrm {sn} (u;k)=-{\vartheta \vartheta _{11}(z;\tau ) \over \vartheta _{10}\vartheta _{01}(z;\tau )}}$

${\displaystyle \mathrm {cn} (u;k)={\vartheta _{01}\vartheta _{10}(z;\tau ) \over \vartheta _{10}\vartheta _{01}(z;\tau )}}$

${\displaystyle \mathrm {dn} (u;k)={\vartheta _{01}\vartheta (z;\tau ) \over \vartheta \vartheta _{01}(z;\tau )}}$

となる。

これで、ヤコビの関数が母数k(τ)の式で定義されたので、これを反転して τ を k の式で表す必要がある。初めに、余母数${\displaystyle k'={\sqrt {1-k^{2}}}}$を考える。これは τ の関数として、

${\displaystyle k'(\tau )=\left({\vartheta _{01} \over \vartheta }\right)^{2}}$

と書ける。

次に、

${\displaystyle \ell ={1 \over 2}{1-{\sqrt {k'}} \over 1+{\sqrt {k'}}}={1 \over 2}{\vartheta -\vartheta _{01} \over \vartheta +\vartheta _{01}}}$

と定める。

そして、ノーム q を ${\displaystyle q=\exp(\pi i\tau )}$ と定義し、ノーム q に関して、${\displaystyle \ell }$を冪級数の商に展開すると、

${\displaystyle \ell ={q+q^{9}+q^{25}+\cdots \over 1+2q^{4}+2q^{16}+\cdots }}$

となる。

級数の反転（英語版）を行うと、

${\displaystyle q=\ell +2\ell ^{5}+15\ell ^{9}+150\ell ^{13}+1707\ell ^{17}+20910\ell ^{21}+268616\ell ^{25}+\cdots }$

を得る。

τの虚部が 1/2 sqrt(3) 以上の場合に帰着すればよいので、q の絶対値は exp(-1/2 sqrt(3) π) ~ 0.0658 以下である場合だけを考えればよい。この値は小さいため、上の級数は急速に収束し、簡単にqの値を計算することができる。

その他の関数

関数名の文字の順序を反転した場合は、元の関数の逆数となる。

${\displaystyle {\begin{aligned}\operatorname {ns} (u)&={\frac {1}{\operatorname {sn} (u)}}\\[8pt]\operatorname {nc} (u)&={\frac {1}{\operatorname {cn} (u)}}\\[8pt]\operatorname {nd} (u)&={\frac {1}{\operatorname {dn} (u)}}\end{aligned}}}$

同様に、上の3つの関数どうしの比は、分子の関数の最初の文字と分母の関数の最初の文字を繋げたものになる。

Elliptic Jacobi function, sc, k = 0.8

${\displaystyle {\begin{aligned}\operatorname {sc} (u)&={\frac {\operatorname {sn} (u)}{\operatorname {cn} (u)}}\\[8pt]\operatorname {sd} (u)&={\frac {\operatorname {sn} (u)}{\operatorname {dn} (u)}}\\[8pt]\operatorname {dc} (u)&={\frac {\operatorname {dn} (u)}{\operatorname {cn} (u)}}\\[8pt]\operatorname {ds} (u)&={\frac {\operatorname {dn} (u)}{\operatorname {sn} (u)}}\\[8pt]\operatorname {cs} (u)&={\frac {\operatorname {cn} (u)}{\operatorname {sn} (u)}}\\[8pt]\operatorname {cd} (u)&={\frac {\operatorname {cn} (u)}{\operatorname {dn} (u)}}\end{aligned}}}$

もっと簡単に、

${\displaystyle \operatorname {pq} (u)={\frac {\operatorname {pr} (u)}{\operatorname {qr} (u)}}}$

と書くことができる。ここで、p、q、r は、s、c、d、n の任意の文字で、ss = cc = dd = nn = 1 と解釈する。

（この記法は、クリストフ・グーデルマン（英語版）とGlaisher（英語版）によるもので、ヤコビの元々の記法にはない）

加法定理

ヤコビの楕円関数が持つ代数的な関係式として

${\displaystyle \operatorname {cn} ^{2}(u,k)+\operatorname {sn} ^{2}(u,k)=1}$

${\displaystyle \operatorname {dn} ^{2}(u,k)+k^{2}\ \operatorname {sn} ^{2}(u,k)=1}$

がある。

これらの方程式で定まる2つの二次曲面の共通部分は楕円曲線であり、(cn, sn, dn)は楕円曲線のパラメタ表示を与えることが分かる。ヤコビの楕円関数の加法定理により、この楕円曲線の点は群となる。

${\displaystyle {\begin{aligned}\operatorname {cn} (x+y)&={\operatorname {cn} (x)\;\operatorname {cn} (y)-\operatorname {sn} (x)\;\operatorname {sn} (y)\;\operatorname {dn} (x)\;\operatorname {dn} (y) \over {1-k^{2}\;\operatorname {sn} ^{2}(x)\;\operatorname {sn} ^{2}(y)}},\\[8pt]\operatorname {sn} (x+y)&={\operatorname {sn} (x)\;\operatorname {cn} (y)\;\operatorname {dn} (y)+\operatorname {sn} (y)\;\operatorname {cn} (x)\;\operatorname {dn} (x) \over {1-k^{2}\;\operatorname {sn} ^{2}(x)\;\operatorname {sn} ^{2}(y)}},\\[8pt]\operatorname {dn} (x+y)&={\operatorname {dn} (x)\;\operatorname {dn} (y)-k^{2}\;\operatorname {sn} (x)\;\operatorname {sn} (y)\;\operatorname {cn} (x)\;\operatorname {cn} (y) \over {1-k^{2}\;\operatorname {sn} ^{2}(x)\;\operatorname {sn} ^{2}(y)}}.\end{aligned}}}$

関数の二乗のもつ関係式

${\displaystyle -\operatorname {dn} ^{2}(u)+m_{1}=-m\;\operatorname {cn} ^{2}(u)=m\;\operatorname {sn} ^{2}(u)-m}$

${\displaystyle -m_{1}\;\operatorname {nd} ^{2}(u)+m_{1}=-mm_{1}\;\operatorname {sd} ^{2}(u)=m\;\operatorname {cd} ^{2}(u)-m}$

${\displaystyle m_{1}\;\operatorname {sc} ^{2}(u)+m_{1}=m_{1}\;\operatorname {nc} ^{2}(u)=\operatorname {dc} ^{2}(u)-m}$

${\displaystyle \operatorname {cs} ^{2}(u)+m_{1}=\operatorname {ds} ^{2}(u)=\operatorname {ns} ^{2}(u)-m}$

ここで、m + m₁ = 1 and m = k²である。

pq² · qp² = 1 と pq = pr / qr を使うことで、二乗についてのさらなる関係式を得られる。ここで、p、q、rは s、c、d、n の任意の文字であり、ss = cc = dd = nn = 1 とする。

ノームに関する展開

ノームを${\displaystyle q=\exp(-\pi K'/K)}$とし、引数を${\displaystyle v=\pi u/(2K)}$と変換する。このときの関数の展開はランベルト級数（英語版）になる。

${\displaystyle \operatorname {sn} (u)={\frac {2\pi }{K{\sqrt {m}}}}\sum _{n=0}^{\infty }{\frac {q^{n+1/2}}{1-q^{2n+1}}}\sin((2n+1)v),}$

${\displaystyle \operatorname {cn} (u)={\frac {2\pi }{K{\sqrt {m}}}}\sum _{n=0}^{\infty }{\frac {q^{n+1/2}}{1+q^{2n+1}}}\cos((2n+1)v),}$

${\displaystyle \operatorname {dn} (u)={\frac {\pi }{2K}}+{\frac {2\pi }{K}}\sum _{n=1}^{\infty }{\frac {q^{n}}{1+q^{2n}}}\cos(2nv).}$

非線形常微分方程式の解としてのヤコビの楕円関数

ヤコビの楕円関数を微分すると、

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\,\mathrm {sn} \,(z)=\mathrm {cn} \,(z)\,\mathrm {dn} \,(z)}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\,\mathrm {cn} \,(z)=-\mathrm {sn} \,(z)\,\mathrm {dn} \,(z)}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} z}}\,\mathrm {dn} \,(z)=-k^{2}\mathrm {sn} \,(z)\,\mathrm {cn} \,(z)}$

となる。

上記の加法定理を使うと、k が 0 < k < 1 を満たす場合は、ヤコビの楕円関数は下記の非線形常微分方程式の解となる。

• ${\displaystyle \mathrm {sn} \,(x)}$ は次の微分方程式の解である

${\displaystyle {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1+k^{2})y-2k^{2}y^{3}=0}$

や

${\displaystyle \left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(1-y^{2})(1-k^{2}y^{2})}$

• ${\displaystyle \mathrm {cn} \,(x)}$ は次の微分方程式の解である

${\displaystyle {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}+(1-2k^{2})y+2k^{2}y^{3}=0}$

や

${\displaystyle \left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(1-y^{2})(1-k^{2}+k^{2}y^{2})}$

• ${\displaystyle \mathrm {dn} \,(x)}$ は次の微分方程式の解である

${\displaystyle {\frac {\mathrm {d} ^{2}y}{\mathrm {d} x^{2}}}-(2-k^{2})y+2y^{3}=0}$

や

${\displaystyle \left({\frac {\mathrm {d} y}{\mathrm {d} x}}\right)^{2}=(y^{2}-1)(1-k^{2}-y^{2})}$

逆関数

ヤコビの楕円関数の逆関数は逆三角関数と同様のやり方で定義される。${\displaystyle x=\mathrm {sn} (\xi ,k)}$に対して、${\displaystyle \xi =\mathrm {arcsn} (x,k)}$である。これらの逆関数は楕円積分で表すことができる^[4][5]。また、冪級数でも表現できる^[6]。

地図投影法

パース・クインカンシャル図法はヤコビの楕円関数を用いた投影法である。また各国で標準的に使われているガウス・クリューゲル図法でも、投影式をヤコビの楕円関数で表すことができる。

脚注

1. 戸田 2001, p. 28.
2. これはそのまま「エスエヌ」と読む^[1]。
3. http://nbviewer.ipython.org/github/empet/Math/blob/master/DomainColoring.ipynb
4. Reinhardt, W. P.; Walker, P. L. (2010), “§22.15 Inverse Functions”, in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, http://dlmf.nist.gov/22.15
5. Ehrhardt, Wolfgang. “The AMath and DAMath Special Functions: Reference Manual and Implementation Notes”. p. 42. 17 July 2013閲覧。
6. Carlson, B. C. (2008). “Power series for inverse Jacobian elliptic functions”. Mathematics of Computation 77: 1615–1621. doi:10.1090/s0025-5718-07-02049-2. http://www.ams.org/journals/mcom/2008-77-263/S0025-5718-07-02049-2/S0025-5718-07-02049-2.pdf 17 July 2013閲覧。.

参考文献

• 戸田盛和『楕円関数入門』日本評論社、2001年。ISBN 4-535-60128-3。
• Abramowitz, Milton [in 英語]; Stegun, Irene Ann [in 英語], eds. (1983) [June 1964]. "Chapter 16". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 569. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253。
• N. I. Akhiezer（英語版）, Elements of the Theory of Elliptic Functions, (1970) Moscow, translated into English as AMS Translations of Mathematical Monographs Volume 79 (1990) AMS, Rhode Island ISBN 0-8218-4532-2
• A. C. Dixon（英語版） The elementary properties of the elliptic functions, with examples (Macmillan, 1894)
• A. G. Greenhill（英語版） The applications of elliptic functions (London, New York, Macmillan, 1892)
• H. Hancock Lectures on the theory of elliptic functions (New York, J. Wiley & sons, 1910)
• Jacobi, C. G. J. (1829) (Latin), Fundamenta nova theoriae functionum ellipticarum, Königsberg, ISBN 978-1-108-05200-9, Reprinted by Cambridge University Press 2012, https://archive.org/details/fundamentanovat00jacogoog
• Reinhardt, William P.; Walker, Peter L. (2010), “Jacobian Elliptic Functions”, in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, http://dlmf.nist.gov/22
• E. T. Whittaker and G. N. Watson（英語版） A Course of Modern Analysis（英語版）, (1940, 1996) Cambridge University Press. ISBN 0-521-58807-3
• （フランス語） P. Appell（英語版） and E. Lacour Principes de la théorie des fonctions elliptiques et applications (Paris, Gauthier Villars, 1897)
• （フランス語） G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 1) (Paris, Gauthier-Villars, 1886–1891)
• （フランス語） G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 2) (Paris, Gauthier-Villars, 1886–1891)
• （フランス語） G. H. Halphen Traité des fonctions elliptiques et de leurs applications (vol. 3) (Paris, Gauthier-Villars, 1886–1891)
• （フランス語） J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome I, Introduction. Calcul différentiel. Ire partie (Paris : Gauthier-Villars et fils, 1893)
• （フランス語） J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome II, Calcul différentiel. IIe partie (Paris : Gauthier-Villars et fils, 1893)
• （フランス語） J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome III, Calcul intégral. Ire partie, Théorèmes généraux. Inversion (Paris : Gauthier-Villars et fils, 1893)
• （フランス語） J. Tannery and J. Molk Eléments de la théorie des fonctions elliptiques. Tome IV, Calcul intégral. IIe partie, Applications (Paris : Gauthier-Villars et fils, 1893)
• （フランス語） C. Briot and J. C. Bouquet Théorie des fonctions elliptiques ( Paris : Gauthier-Villars, 1875)

関連項目

• 楕円積分
• 楕円曲線
• Schwarz–Christoffel mapping（英語版）
• Carlson symmetric form（英語版）
• ヴァイエルシュトラスの楕円函数
• ヤコビのテータ関数
• ラマヌジャンのテータ関数（英語版）

外部リンク

• Hazewinkel, Michiel, ed. (2001), “Jacobi elliptic functions”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Jacobi_elliptic_functions
• Weisstein, Eric W. "Jacobi Elliptic Functions". mathworld.wolfram.com (英語).
• ヤコビ楕円関数 - サンプルソースコード C/C++
• ヤコビ楕円関数 - サンプルソースコード Fortran