Remove ads
ケイリー＝バッハラッハの定理（ケイリー＝バッハラッハのていり[1]、英: Cayley–Bacharach theorem）は数学における射影平面P2上の三次曲線に関する定理。
- 射影平面上の2つの3次曲線C1,C2が、異なる9つの点で交わっているとする。この9点のうち8点を通る3次曲線は他の9番目の点を通る。
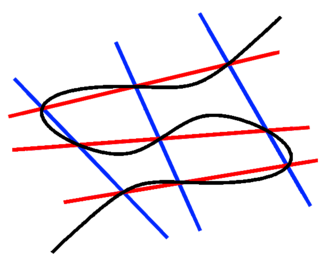
ケイリー＝バッハラッハの本質的な形式は次のように導かれる。
- 与えられた8点P1, ..., P8を通る代数的閉体上のすべての3次曲線Cは、P1, ..., P8に依存するある点P9を通る。
ミシェル・シャールは最初に円錐曲線の場合の定理を証明した。その後アーサー・ケイリーとイザーク・バッハラッハによって一般化された[2]。ケイリーの証明には、重大な見落としがあった。バッハラッハはアレクサンダー・フォン・ブリルとマックス・ネーターの研究に基づき、ケイリーの証明を改善し、1881年に正しい一般化を示した[3]。
ベズーの定理より、三次曲線は二次曲線を含むため、P1, ..., P8のうち7点が円錐曲線上にあるならば、9つ目の点をその円錐曲線上に選ぶことができる。そうでない場合は次のようになる。
この場合、P1, ..., P8を通るすべての3次曲線は、同様にP1, ..., P8を通る異なる2つの三次曲線の9番目の交点を通る。ベズーの定理によれば2つの3次曲線には代数的閉包上に必ず9つの交点が存在する。
円錐曲線が1,2直線に退化したならば、退化した円錐曲線上の7点のうち、少なくとも4点は共線である。よって次の結果を得る。
一方で、P1, P2, P3, P4が共線で、8点P1, ..., P8のうちどの7点も非退化円錐曲線上にない場合を考えると、8点のうちどの5点も共線でなく、また、P5, P6, P7, P8のうちどの3点も共線でない。ベズーの定理によれば、3次曲線は直線を含むから、P1, ..., P8（のアフィン凸錐上）で0を取る三次斉次多項式のベクトル空間は、P5, P6, P7, P8（のアフィン凸錐上）で0を取る2次元の二次斎次多項式ベクトル空間と同型である。
2次元の結果の条件とは異なるものの、どちらも、一般の位置にある場合よりも弱い結果である。上記の結果は3点が共線であること、6点が同一円錐曲線上にあることを許す場合である。 ケイリー＝バッハラッハの定理の成立条件は、ただ9点を通る3次曲線の族であることが条件である。
ベズーの定理によれば、代数的閉体上の既約でない異なる2つの3次曲線は重複を含め、常に9点で交わる。したがって、ケイリー＝バッハラッハの定理は、どの7点も同一円錐曲線にない8つの交点を与えたとき、曲線の族内の任意の2つの交点の最後の点は不動であることを主張する。
Remove ads
ケイリー＝バッハラッハの定理の特殊な場合にパスカルの定理がある。パスカルの定理は円錐曲線上に6点P1, ..., P6を取ったとき、P1P2とP4P5、P2P3とP5P6、P3P4とP6P1の交点は共線であるという定理である。3次曲線の1つを3直線に退化させ、6つの交点を円錐曲線上に配置すれば、（もう一方の3次曲線をその円錐曲線とある1本の直線として）ケイリー＝バッハラッハの定理より残り3つの交点が共線になる。
パップスの六角形定理は、上述の円錐曲線をさらに2直線に退化させることで示される。
ケイリー＝バッハラッハの定理の上記の3番目の場合は楕円曲線の点の加法性により証明できる。1つめの3次曲線を3直線BC, O(A+B), A(B+C)とする。8点A, B, C, A+B, -A-B, B+C, -B-C, Oは、2つの3次曲線の共通の点である。9つ目の点は-A-(B+C)=-(A+B)-Cとなって一致する。
ケイリー＝バッハラッハの定理と、それが3次曲線で起きる理由は次元の勘定から説明できる。9つの点は一意的な三次曲線を決定する。したがって、9つの点が2つ以上の3次曲線上にある場合、つまり2つの3次曲線の（3 × 3 = 9つの）交点である場合、この点らは一般の位置にはないこと、1次元の過剰な決定 があることを意味する。そして、この9点を通る3次曲線は"eight implies nine"という特性を満たすように、さらなる条件を満たす。これを一般に過剰度（superabundance）という。過剰度については曲面のリーマン・ロッホの定理を見よ。
詳細
形式的には、まず、d次の2つの曲線が与えられたとき、方程式の線型結合でそれらがd次の束（1変数の線形システム）を成すことを考える。これは曲線の母数空間（あるいは単に射影空間）上の射影直線を決定する2点に対応する。
ケイリー＝バッハラッハの定理は高次においても起こる。これはd次の2曲線の交点の個数d 2が 次数dの曲線を決定する点の個数より早く成長するためである。次数dの曲線を決定する点の個数は次式で与えられる。
d = 3の場合がケイリー＝バッハラッハの定理に対応する。より高次の場合でもd 2はこの数より大きいので、ケイリー＝バッハラッハの定理はより高次に一般化される。
具体的には、d次の曲線の決定に必要な点の個数は、d次の単項式の数から1を引いた数である。小さいdにおいては以下の様な計算になる。
- d = 1: 2と1: 2点が直線を決定し、2直線は一点で交わる。
- d = 2: 5と4: 5点が円錐を決定し、2つの円錐曲線は4点で交わる。
- d = 3: 9と9: 9点が三次曲線を決定し、2つの3次曲線は9点で交わる。
- d = 4: 14と16.
したがってケイリー＝バッハラッハの定理が起きる最初の数は3で、d > 3のとき、交点の数が曲線の決定に必要な数を上回る。
これは3次曲線が高次の代数曲線より猶更特別であることを意味する。より低い次数、1次の場合は、2直線は1点で交わるが、これは一般的な位置にある。2次曲線も4点で交わるが、二次曲線が既約で、交点が共線でないとするならば、これも一般的な位置である。5つの条件が2次方程式を決定するので、4点では、曲線の方程式が決まらないからである（4点を通る二次曲線の束を成す）。一方、3次方程式は9つの条件で決定されるため、ある9つの点を通る3次曲線が束を成すということは、その9点が特別な位置にあることということになる。 したがって解となる空間の次元は1つ高くなり、追加の条件"8 implies 9"を導く。
より具体的には、x, y, zを変数とする3次の斉次多項式P(x, y, z)のベクトル空間は10次元を持つので、異なる8点を通る3次曲線の系は2次以上のベクトル空間で媒介変数表示される （ある点で多項式が0になることは1つの線型条件を課す）。 これは、どの4点も共線でないかつ、どの7点も円錐曲線上にないならば、2次になることを導ける。ケイリー＝バッハラッハの定理はこの事実から演繹される[4]。
Remove ads
- 因子の一次系
- ゴレンシュタイン環
- クラメールのパラドックス
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
Remove ads