Spirale aurea

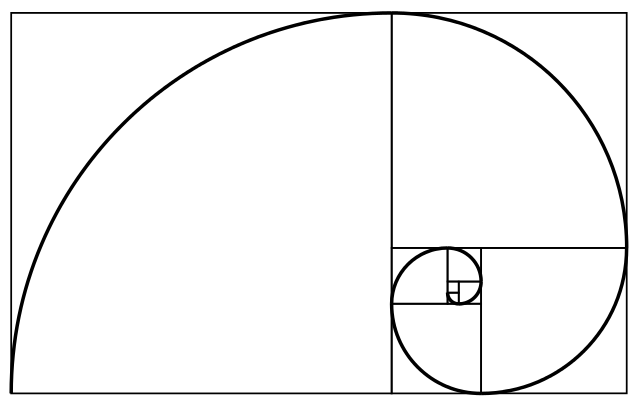
In geometria, la spirale aurea è un tipo particolare di spirale logaritmica con fattore di accrescimento b pari a φ, la sezione aurea.^[1]

Rettangolo aureo, poligonale aurea e spirali auree inscritta e circoscritta. Si notano le due diagonali (in rosso) che individuano l'origine delle tre spirali. La poligonale aurea ha i lati che si riducono secondo il rapporto aureo. Le altre due spirali sono una circoscritta e l'altra inscritta alla poligonale. Quella inscritta inizia dallo stesso punto (P) dal quale si fanno iniziare i quarti di circonferenza che approssimano la spirale aurea. Come evidenziato dai tratti rossi la spirale aurea se inizia in (P) sborda dalla poligonale, questo mostra che al contrario della versione approssimata con archi di circonferenza non può iniziare o passare per (P). Il punto di tangenza corretto con la poligonale risulta quindi anticipato rispetto a (P), vedi angolo di circa 17⁰. Se la qualità dell'immagine non è soddisfacente, selezionandola dovrebbe migliorare.

Spirale poligonale aurea con passo angolare 90⁰ come base per la costruzione semplificata della spirale aurea approssimata con archi di cerchio. L'animazione mostra la spirale poligonale aurea che offre i suoi vertici come centro per gli archi di circonferenza che realizzano l'approssimazione della spirale aurea. In particolare si notano gli archi di circonferenza (blu) che seguendo lo sviluppo della spirale poligonale (verde) approssimano la spirale aurea, già rappresentata con tratto nero. Se la qualità dell'immagine non è soddisfacente, selezionandola dovrebbe migliorare.

Spirali auree vere e approssimate: la spirale verde è formata da quarti di circonferenze inscritte in dei quadrati; la spirale rossa è una spirale aurea, un particolare tipo di spirale logaritmica. Sovrapponendo le due spirali si ottiene la spirale gialla.

Formula

L'equazione polare di una spirale aurea è la stessa delle altre spirali logaritmiche, ma con un particolare valore di b:^[2]

${\displaystyle r=ae^{b\theta }}$

oppure

${\displaystyle \theta ={\frac {1}{b}}\ln(r/a),}$

dove e è la base dei logaritmi naturali, a è una costante reale arbitraria, ma positiva, e b è tale che quando θ è un angolo retto, la quantità:

${\displaystyle e^{b\theta _{\mathrm {right} }}\,=\phi }$

La quantità ${\displaystyle \phi }$ è il fattore che descrive di quanto aumenta il raggio della spirale dopo aver compiuto un angolo retto, ovvero un quarto di giro. Se per esempio imponiamo ${\displaystyle \phi =2}$, ciò significa che in questo caso la spirale raddoppia il proprio raggio ad ogni quarto di giro e quindi ad ogni giro completo le sue dimensioni aumentano di un fattore ${\displaystyle 16=\phi ^{4}=2^{4}}$.

Perciò, b è dato da

${\displaystyle b={\ln {\phi } \over \theta _{\mathrm {right} }}.}$

Utilizzando questa definizione l'equazione della spirale logaritmica diventa^[3]:

${\textstyle r(\theta )=ae^{{\frac {\ln {\phi }}{\theta _{right}}}\theta }=a\phi ^{\frac {\theta }{\theta _{right}}}=a\phi ^{\frac {2\theta }{\pi }},}$

in quanto ${\displaystyle \theta _{right}={\frac {\pi }{2}}}$.

Calcolando il rapporto tra ${\displaystyle r(\theta +{\dfrac {\pi }{2}})}$e ${\displaystyle r(\theta )}$infatti si ottiene:

${\displaystyle {\dfrac {r(\theta +{\dfrac {\pi }{2}})}{r(\theta )}}={\dfrac {a\phi ^{\frac {2(\theta +{\frac {\pi }{2}})}{\pi }}}{a\phi ^{\frac {2\theta }{\pi }}}}={\dfrac {a\phi ^{\frac {2\theta }{\pi }}\phi }{a\phi ^{\frac {2\theta }{\pi }}}}=\phi }$

Il che dimostra come nella forma ${\textstyle r(\theta )=a\phi ^{\frac {2\theta }{\pi }},}$la quantità ${\textstyle \phi }$ sia il fattore che descrive di quanto aumenta il raggio ogni quarto di giro.

La spirale aurea è quindi un caso particolare della spirale logaritmica, ovvero il caso in cui ${\displaystyle \phi }$, al posto di essere un numero reale positivo generico, assume il valore della sezione aurea:

${\displaystyle \phi ={\dfrac {1+{\sqrt {5}}}{2}}}$

Il valore numerico del modulo di b per la spirale aurea vale:

Una spirale di Fibonacci approssima la spirale aurea; al contrario del diagramma con i rettangoli basato sulla sezione aurea, questa spirale si basa su quadrati di lato pari a numeri di Fibonacci.

${\displaystyle |b|={\ln {\phi } \over 90}=0.0053468}$ per θ espresso in gradi;

${\displaystyle |b|={\ln {\phi } \over \pi /2}=0.306349}$ per θ espresso in radianti.