Projection gnomonique

En géométrie et en cartographie, une projection gnomonique est une projection cartographique azimutale transformant les grands cercles en lignes droites ; le trajet le plus court entre deux points de la sphère correspond donc à celui sur la carte.

La projection gnomonique transforme les grands cercles en droites.

Historique et applications

La projection gnomonique serait la plus ancienne projection cartographique ; elle aurait été développée par Anaximandre^[1] au VI^e siècle av. J.-C. L'ombre de la pointe d'un gnomon trace les mêmes hyperboles que celles formées par les parallèles d'une carte gnomonique, d'où son nom.

Les projections gnomoniques sont naturellement utilisées en gnomonique et aussi en sismologie, parce que les ondes sismiques tendent à se propager le long de grands cercles. Elles sont aussi utilisées en navigation pour la radiogoniométrie, les signaux radios se propageant également le long de grands cercles. Il en est de même des météorites, c'est pourquoi l'Atlas gnomonique Brno 2000.0 est l'ensemble de cartes stellaires que recommande l'IMO pour les observations visuelles de météorites.

En 1946, Buckminster Fuller breveta une méthode de projection similaire (il s'agit en fait du recollement de plusieurs projections gnomoniques) dans sa version cuboctaédrale de la Dymaxion Map. Il en publia une version icosaédrale en 1954, intitulée AirOcean World Map, qui est celle à laquelle il est le plus souvent fait référence actuellement.

Définition géométrique

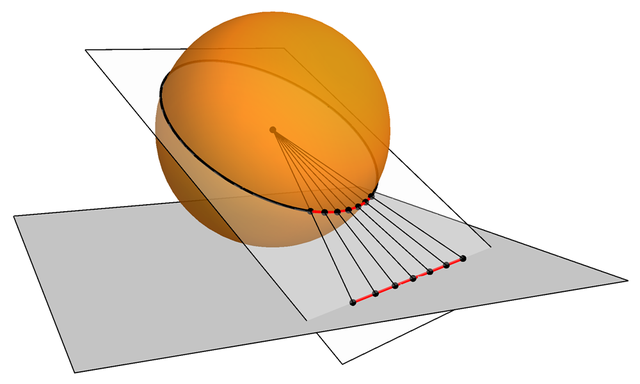
La projection gnomonique de la sphère de centre C sur un de ses plans tangents (au point T) est la transformation qui associe à chaque point A de la sphère l'intersection P de la droite (CA) avec ce plan. La projection n'est pas définie pour les points du grand cercle parallèle au plan tangent^[2] ; en cartographie, on ne représente ainsi que le demi-hémisphère pour lequel A est situé entre C et P ; on dit que la projection est centrée en T, et c'est en ce point que la déformation de la projection est la plus faible.

Comme chaque grand cercle de la sphère est l'intersection de celle-ci avec un plan passant par le centre, sa projection est l'intersection de ce plan avec le plan tangent, et donc une ligne droite ; c'est en particulier le cas des méridiens et de l'équateur :

• si le point de tangence est l'un des pôles (comme sur la projection ci-contre), les méridiens passent par le centre et sont régulièrement espacés ; l'équateur est rejeté à l'infini. Les parallèles deviennent des cercles concentriques (voir la figure 1 ci-dessous) ;
• si le point de tangence est sur l'équateur, les méridiens sont des droites parallèles, mais non régulièrement espacées, et seul l'équateur devient une droite perpendiculaire aux méridiens. Les autres parallèles sont représentés comme des arcs d'hyperboles (voir la figure 2 ci-dessous) ;
• dans les autres cas, les méridiens sont des (demi-)droites partant toutes du pôle, mais non régulièrement espacées ; la droite représentant l'équateur n'est orthogonale qu'à l'un de ces méridiens (ce qui montre que la projection gnomonique n'est pas une transformation conforme) ; enfin, les autres parallèles peuvent, suivant leur position, être représentés par une droite ou des paraboles (aux latitudes les plus proches de l'équateur), un arc d'hyperbole (à la latitude limite spécifique du point de tangence), ou bien des ellipses (aux latitudes supérieures) dont les centres sont alignés sur la demi-droite verticale représentant le méridien opposé (voir la figure 3 ci-dessous).

• 
  Figure 1. Projection gnomonique polaire (centrée ici au pôle nord). L'échelle radiale (écartement depuis le pôle des cercles concentriques représentant les parallèles géographiques) croit plus vite que l'échelle transversale (écartement angulaire des demi-droites représentant les méridiens depuis le pôle). Les déformations vers les bords de la carte sont identiques dans toutes les directions depuis le centre.
• 
  Figure 2. Projection gnomonique équatoriale, dite aussi transversale (centrée ici sur l'intersection du méridien de Greenwich et de l'équateur). L'échelle radiale (écartement des arcs d'hyperboles représentant les parallèles géographiques) croit plus vite que l'échelle transversale (écartement des droites parallèles verticales représentant les méridiens géographiques). Les déformations sont plus importantes vers les bords verticaux de la carte à droite ou gauche que vers les bords horizontaux en haut et en bas.
• 
  Figure 3. Projection gnomonique oblique (centrée ici sur un point de l'île centrale du Japon). Le parallèle géographique passant par le Japon est un arc d'hyperbole, ceux au nord du Japon sont projetés en ellipses, l'équateur est représenté par une droite horizontale dont le point central sur la carte correspond à la péninsule ouest de la Papouasie occidentale en Indonésie, les autres parallèles au sud du Japon sont représentés en hyperboles axées sur le méridien central et réparties de chaque côté de l'équateur.

Comme pour toutes les projections azimutales, les angles au point de tangence sont conservés. La distance sur la carte à partir de ce point est une fonction r(d) de la distance réelle d, donnée par

${\displaystyle r(d)=\mathrm {R} \cdot \tan(d/\mathrm {R} )}$,

où R est le rayon terrestre. L'échelle radiale est :

${\displaystyle r'(d)={\frac {1}{\cos ^{2}(d/\mathrm {R} )}}}$

et l'échelle transversale est :

${\displaystyle {\frac {1}{\cos(d/\mathrm {R} )}}\$ ;}

les deux échelles augmentent en s'éloignant du centre, mais l'échelle radiale augmente plus vite.

Dans tous les cas, la projection ne peut pas représenter sur la même carte plus d'une seule hémisphère géographique dont les limites sont projetées hors de la carte à l'infini.

Notes

1. Strabon, Géographie, Livre 1.
2. Il est possible de généraliser cette transformation en ajoutant au plan tangent une droite à l'infini (image de ce grand cercle), le transformant en un plan projectif.

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Gnomonic projection » (voir la liste des auteurs).

• (en) Snyder, John P., Map Projections - A Working Manual. U.S. Geological Survey Professional Paper 1395, United States Government Printing Office, Washington, D.C, 1987 Cet article peut être téléchargé à partir des pages de l'USGS

Voir aussi

Les trois autres projections azimutales principales :

• Projection orthographique
• Projection azimutale équivalente de Lambert
• Projection stéréographique

Liens externes

• (en) http://www.bfi.org/node/25 Description de la projection de Fuller, du Buckminster Fuller Institute
• http://www.nautischool.ch/pdf/AC_FS_projection_carto.pdf Étude des projections par l'ENMM du Havre
• (en) http://erg.usgs.gov/isb/pubs/MapProjections/projections.html#gnomonic Explications des projections par l'USGS
• (en) http://exchange.manifold.net/manifold/manuals/6_userman/mfd50Gnomonic.htm
• (en) http://mathworld.wolfram.com/GnomonicProjection.html
• (en) http://members.shaw.ca/quadibloc/maps/maz0201.htm
• (en) Table d'exemples et de propriétés des projections usuelles, à radicalcartography.net

• Portail de la géométrie
• Portail de la cartographie