Pression de rayonnement

La pression de rayonnement ou pression radiative est la pression mécanique exercée sur une surface quelconque par l'échange de quantité de mouvement entre l'objet et le champ électromagnétique. Cela comprend l'impulsion de la lumière ou du rayonnement électromagnétique de toute longueur d'onde qui est absorbée, réfléchie ou émise d'une autre manière (par exemple, le rayonnement du corps noir) par la matière à toute échelle (des objets macroscopiques aux particules de poussière en passant par les molécules de gaz)^[1],[2],[3].

La force exercée sur un réflecteur résulte de la réflexion du flux de photons. La figure présente le cas d'une surface réfléchissant totalement le rayonnement de façon spéculaire.

Cette pression est l'analogue pour le rayonnement de la pression gazeuse et, comme elle, associée au transfert de quantité de mouvement volumique dans une direction de propagation donnée, plus précisément au flux de cette quantité. Son unité est le pascal (Pa).

Il s'agit donc d'une quantité thermodynamique, même si elle est intimement liée à la description donnée par l'électromagnétisme. C'est à cause de ce lien que l'on parle par extension de pression exercée sur une particule de faible dimension (du même ordre de grandeur que la longueur d'onde), phénomène accessible seulement à l'électromagnétisme.

Cette notion est utilisée dans de nombreux domaines liés à la physique des plasmas, l'astrophysique et la physique stellaire^[4]. L'aspect électromagnétique est présent dans la manipulation de particules.

Les forces générées par la pression de rayonnement sont généralement trop faibles pour être remarquées dans les circonstances quotidiennes ; cependant, elles sont importantes dans certains processus physiques. C'est le cas notamment des objets situés dans l'espace où, outre la gravité, c'est généralement la principale force agissant sur les objets et où l'effet net d'une force minuscule peut avoir un effet cumulatif important sur de longues périodes. Par exemple, si les effets de la pression de radiation du soleil sur le vaisseau spatial du programme Viking avaient été ignorés, le vaisseau spatial aurait manqué l'orbite de Mars d'environ 15 000 km^[5]. La pression de radiation de la lumière des étoiles est également cruciale dans un certain nombre de processus astrophysiques. L'importance de la pression de rayonnement augmente rapidement à des températures extrêmement élevées, et peut parfois éclipser l'habituelle pression de gaz, par exemple dans les intérieurs stellaires et armes thermonucléaires.

Historique

Le premier à avancer un effet dynamique du rayonnement a été Johannes Kepler qui expliqua l'orientation des queues cométaires par le flux du rayonnement solaire (1619)^[6].

Les efforts engendrés par une onde électromagnétique sur une paroi furent expliqués théoriquement par James Maxwell en 1873^[7]. Par la suite les efforts ont porté sur le lien entre approche électromagnétique et thermodynamique ou physique statistique. Les premières tentatives de mesure de pression par une approche thermodynamique sont dues à Adolfo Bartoli en 1884^[8] et Pyotr Lebedev en 1900^[9]. Les expériences importantes ont été faites par Ernest Nichols et Gordon Hull (en) qui ont montré le lien entre énergie et quantité de mouvement incident sur une surface en mesurant simultanément l'énergie par bolométrie et quantité de mouvement grâce à un radiomètre développé à cet effet (radiomètre de Nichols) en 1901^[10] et 1903^[11].

Préambule

La pression gazeuse ou radiative est classiquement définie comme une force générée par le phénomène, rapportée à la surface sur laquelle elle s'exerce. Ceci n'est pas physiquement et logiquement correct :

• les transferts de quantité de mouvement dans un rayonnement existent en l'absence de paroi. Ils sont importants dans les milieux très chauds rencontrés en physique des plasmas et astrophysique. Il faut donc définir la notion de pression radiative utilisée dans le cadre du problème de transfert radiatif ;
• l'effet sur une paroi solide dépend du rayonnement incident mais aussi des propriétés de cette surface : absorptivité, type de réflectivité (spéculaire, diffuse, etc.). Il y a une relation causale mais pas de relation biunivoque entre pression et force résultante.

Par souci de rigueur on va donc donner une définition formelle basée sur la nature du phénomène, à savoir le flux de quantité de mouvement volumique d'un ensemble de photons.

Bien entendu l'aspect électromagnétique est sous-jacent et on peut (dans certains cas on doit) calculer la force exercée sur une paroi ou une particule à partir des équations de Maxwell. On parle encore dans ce cas de pression de rayonnement bien que cela ne corresponde pas à une variable physique naturelle.

Définitions

La notion de pression fait appel à la physique statistique et à la thermodynamique. Ceci est vrai pour un gaz formé d'atomes ou de molécules mais aussi pour un gaz de photons.

Luminance, quantité de mouvement

Le rayonnement est caractérisé par le nombre de photons par unité de volume de fréquence comprise entre ν et ν + d ν se déplaçant dans le cône dΩ autour de la direction Ω. Il s'agit donc d'une distribution angulaire f_ν (Ω). 0n utilise la luminance spectrale définie par^{[12],[n 1]}

${\displaystyle L_{\nu }({\boldsymbol {\Omega }})=c\,h\,\nu f_{\nu }({\boldsymbol {\Omega )}}}$

où c est la vitesse de la lumière et h la constante de Planck. Cette quantité est la fonction de base dans l'étude du transfert radiatif.

On peut écrire f_ν sous la forme

${\displaystyle f_{\nu }({\boldsymbol {\Omega }})=n_{\nu }g_{\nu }({\boldsymbol {\Omega }})}$

où n_ν est la densité particulaire et g_ν la distribution angulaire normalisée par intégration sur la sphère unité ${\displaystyle \textstyle \int _{S^{2}}g_{\nu }({\boldsymbol {\Omega }})\mathrm {d} {\boldsymbol {\Omega }}=1}$

Les luminances sont donc sommables comme le nombre de photons car il n'y a pas d'interaction photon-photon.

La quantité de mouvement d'un photon est

${\displaystyle \mathbf {q} ={\frac {h\nu }{c}}\mathbf {\Omega } }$

Elle est donc reliée à la luminance par

${\displaystyle {\frac {L_{\nu }}{c}}=c\,q\,n_{\nu }\,g_{\nu }=p_{\nu }}$

p_ν est une pression radiative spectrale, le flux sur la surface normale à Ω de la densité volumique de quantité de mouvement ${\displaystyle \textstyle q\,n_{\nu }\,g_{\nu }}$. Les pressions sont donc sommables.

On généralise ci-dessous cette notion.

Pression radiative

La pression radiative est le tenseur des contraintes radiatives, d'ordre 2, symétrique, obtenu à partir du produit tensoriel ${\displaystyle \textstyle \mathbf {\Omega } \otimes \mathbf {\Omega } }$ (l'unité de mesure normalisée est le Pa s, puisque c'est une pression définie dans un intervalle spectral)^[13].

${\displaystyle {\mathsf {P}}_{\nu }={\frac {1}{c}}\int _{S^{2}}L_{\nu }\,\mathbf {\Omega } \otimes \mathbf {\Omega } \,\mathrm {d} \mathbf {\Omega } }$

La trace de ce tenseur est l'énergie volumique spectrale

${\displaystyle Tr\left({\mathsf {P}}_{\nu }\right)={\frac {1}{c}}\int _{S^{2}}L_{\nu }\,\mathrm {d} \mathbf {\Omega } \equiv E_{\nu }}$

Deux exemples peuvent illustrer ceci :

• distribution isotrope : ${\displaystyle \textstyle L_{\nu }=L_{\nu _{0}}=C^{ste}}$ alors

${\displaystyle {\mathsf {P}}_{\nu }={\frac {L_{\nu _{0}}}{c}}\int _{4\pi }\,\mathbf {\Omega } \otimes \mathbf {\Omega } \,\mathrm {d} \mathbf {\Omega } ={\frac {L_{\nu _{0}}}{c}}{\frac {4\pi }{3}}\,{\mathsf {I}}\,,\qquad E_{\nu }={\frac {4\pi }{c}}L_{\nu _{0}}}$

où ${\displaystyle \textstyle {\mathsf {I}}}$ est le tenseur unité. Ce tenseur décrit une pression spectrale isotrope.

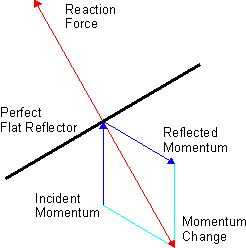
• faisceau de luminance L_ν0 dans la direction Ω₀ = (1, 0, 0) : ${\displaystyle \textstyle L_{\nu }=L_{\nu _{0}}\delta (\mathbf {\Omega } -\mathbf {\Omega } _{0})}$ où δ est la distribution de Dirac alors

${\displaystyle {\mathsf {P}}_{\nu }={\frac {L_{\nu _{0}}}{c}}\int _{4\pi }\,\mathbf {\Omega } \otimes \mathbf {\Omega } \,\delta (\mathbf {\Omega } -\mathbf {\Omega } _{0})\mathrm {d} \mathbf {\Omega } ={\frac {L_{\nu _{0}}}{c}}{\begin{pmatrix}1&0&0\\[0.5em]0&0&0\\[0.5em]0&0&0\end{pmatrix}}\,,\qquad E_{\nu }={\frac {L_{\nu _{0}}}{c}}}$

Ce tenseur décrit une pression égale à ${\displaystyle \textstyle p_{\nu }={\frac {L_{\nu _{0}}}{c}}}$ dans la direction Ω₀, nulle dans tout autre direction.

Bien entendu, toutes ces quantités peuvent être intégrées sur tout ou partie du spectre : on obtient alors une pression totale exprimée en Pa.

${\displaystyle L=\int _{0}^{\infty }L_{\nu }\mathrm {d} \nu \,,\quad {\mathsf {P}}=\int _{0}^{\infty }{\mathsf {P}}_{\nu }\mathrm {d} \nu }$

Exemples

Deux exemples peuvent illustrer ces calculs :

• intérieur du Soleil

Le rayonnement est celui d'un corps noir, donc isotrope. Pour un tel milieu, la luminance totale est ${\displaystyle \textstyle L_{0}={\frac {\sigma T^{4}}{\pi }}}$ d'où ${\displaystyle \textstyle {\mathsf {P}}={\frac {4\sigma T^{4}}{3c}}{\mathsf {I}}}$

Pour une température T ~ 15 MK qui correspond à la valeur dans le noyau, on obtient une pression voisine de 10¹³ Pa. Cette valeur est une partie notable de la pression totale dans le milieu. Dans une étoile plus grosse, elle peut devenir prépondérante ;

• le Soleil au niveau de la Terre

Cette fois, le rayonnement est proche d'un faisceau parallèle : le Soleil de rayon R est vu de la Terre à la distance L sous un angle de ${\textstyle \textstyle \arctan {\left({\frac {2R}{L}}\right)}\simeq 0,5}$° et le spectre proche de celui d'un corps noir à la température T ~ 5 780 K. La pression est donc ${\displaystyle \textstyle {\frac {\sigma T^{4}}{\pi c}}\left({\frac {R}{L}}\right)^{2}\simeq 10^{-6}\;{\text{Pa}}}$.

La pression de radiation solaire est la source dominante de perturbation dans l'espace interplanétaire^[14].

Cette pression de radiation est à distinguer de celle exercée par le vent solaire, qui est un flux de particules de matière^[15].

Effort exercé sur une surface

Approche thermodynamique

La surface est définie par son absorptivité ${\displaystyle 1-r}$ et sa réflectivité ${\displaystyle r}$. Celle-ci peut être généralement décrite comme la somme d'une réflexion spéculaire en part s et d'une réflexion diffuse isotrope. Il s'agit d'une approximation raisonnable dans la plupart des cas. Dans le cas le plus général, on doit utiliser un modèle de réflectivité bidirectionnelle et dans ce cas les calculs deviennent numériques.

Il faut ajouter l'émission propre, généralement (mais non nécessairement) thermique.

Échanges de quantité de mouvement pour un photon

On suppose que le système paroi (exposant S) + photon avant réflexion (exposant 1) et après (exposant 2) conserve la quantité de mouvement. L'indice ν est omis.

${\displaystyle \textstyle \mathbf {q} ^{S}=\mathbf {q} ^{(1)}-\mathbf {q} ^{(2)}}$

Cette relation est projetée sur les axes parallèle (indice //) et perpendiculaire (indice ⊥). Le photon a une incidence θ par rapport à la normale à la surface.

• absorption

${\displaystyle q_{//}^{S}=q_{//}^{(1)}=q\sin {\theta }\,,\qquad q_{\perp }^{S}=q_{\perp }^{(1)}=q\cos {\theta }}$

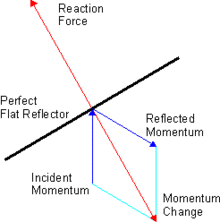
• réflexion spéculaire

${\displaystyle q_{//}^{S}=0\,,\qquad q_{\perp }^{S}=2q_{\perp }^{(1)}=2q\cos {\theta }}$

• réflexion diffuse

${\displaystyle q_{//}^{S}=q_{//}^{(1)}=q\sin {\theta }\,,\qquad q_{\perp }^{S}=q_{\perp }^{(1)}+q\int _{0}^{\frac {\pi }{2}}\sin {\theta }\cos {\theta }\,\mathrm {d} \theta =q\cos {\theta }+{\frac {q}{2}}}$

Au total, pour le rayonnement incident

${\displaystyle q_{//}^{S}=q(1-rs)\sin {\theta }}$

${\displaystyle q_{\perp }^{S}=q\left[(1+rs)\cos {\theta }+{\frac {r}{2}}(1-s)\right]}$

Le rayonnement propre est généralement isotrope. Dans ce cas

${\displaystyle q_{//}^{S}=0\,,\qquad q_{\perp }^{S}={\frac {q}{2}}}$

Passage au niveau pression

L'approche en pression est l'analogue de ce qui précède. En effet, les tenseurs de pression se somment car l'opérateur d'intégration est linéaire. Donc au voisinage de la paroi

${\displaystyle {\mathsf {P}}^{S}={\mathsf {P}}^{(1)}-{\mathsf {P}}^{(2)}}$

où ${\displaystyle {\mathsf {P}}^{(1)}}$ est le tenseur du rayonnement incident et ${\displaystyle {\mathsf {P}}^{(2)}}$ celui du rayonnement quittant la surface.

• absorption : ${\displaystyle {\mathsf {P}}^{(2)}={\mathsf {0}}}$ (tenseur nul)
• réflexion spéculaire : ${\displaystyle {\mathsf {P}}^{(2)}}$ est l'image du rayonnement symétrique de ${\displaystyle {\mathsf {P}}^{(1)}}$, obtenu par un simple changement de signe des termes diagonaux ${\displaystyle {\mathsf {P}}_{kl}^{(2)}=-(-1)^{k+l}{\mathsf {P}}_{kl}^{(1)}}$.
• réflexion diffuse : ${\displaystyle {\mathsf {P}}^{(2)}}$ est isotrope dans un demi-espace. La conservation de l'énergie permet d'écrire

${\displaystyle E^{(2)}={\frac {2\pi }{c}}L^{(2)}=E_{-}^{(1)}}$

où ${\displaystyle E_{-}^{(1)}}$ est l'énergie incidente dans le demi-espace tourné vers la paroi. Donc

${\displaystyle {\mathsf {P}}^{(2)}={\frac {2E_{-}^{(1)}}{3}}\,{\mathsf {I}}}$

Comme pour un seul photon, il ne reste plus qu'à pondérer par les fractions r et s pour obtenir le tenseur de pression résultant (spectral ou total).

Cette méthode a l'avantage de permettre d'effectuer systématiquement des calculs formels ou numériques.

Elle est analogue à la mécanique des fluides, permettant d'obtenir les contributions normale et parallèle des efforts à la paroi (la « pression » et le « cisaillement »).

${\displaystyle \mathbf {F} ={\mathsf {P}}^{S}\cdot \mathbf {x} }$

où x est le vecteur unitaire normal à la surface et F la force (spectrale ou totale) exercée par unité de surface.

Approche électromagnétique

Interaction onde-surface

Une onde électromagnétique incidente interagit par son champ électrique avec le matériau par l'intermédiaire de particules ou quasi-particules du solide au voisinage de la paroi. Il s'agit d'électrons d'une bande de valence pour un métal ou d'un phonon pour un diélectrique. Les oscillations induites provoquent l'émission d'une onde de même fréquence, plus ou moins déphasée, qui interfère avec l'onde incidente. Dans le cas de l'émission, c'est l'agitation thermique qui crée l'onde.

On utilise les équations de Maxwell pour calculer les propriétés des surfaces dont on parle plus haut : réflectivité, absorptivité et émissivité à partir des propriétés intrinsèques du solide^[16] ou son état de surface^[17]. On ne s'en sert que rarement pour évaluer directement des efforts induits.

Interaction onde-atome

Considérons un faisceau laser éclairant un milieu gazeux. Lorsque la longueur d'onde correspond à une raie d'absorption, l'atome acquiert la quantité de mouvement q dans la direction de propagation et passe sur un état d'énergie supérieur. Lors de la désexcitation, l'atome émet un photon de même énergie. L'émission se fait dans une direction quelconque. Donc en moyenne, la quantité de mouvement due à la désexcitation est nulle. Le faisceau accélère le mouvement de chaque atome de la même quantité, là aussi en moyenne. C'est donc la vitesse moyenne (macroscopique) du gaz qui est affectée. La distribution statistique des vitesses microscopiques ne l'est pas.

Pour obtenir un effet de diminution des vitesses microscopiques (donc une baisse de la température du gaz), il faut utiliser une absorption sélective angulairement. Ce phénomène n'est donc pas directement lié à la notion de pression radiative.

Interaction onde-particule

Le cas de particules de taille voisine de la longueur d'onde est différent puisque l'approximation particulaire n'est pas utilisable. Le phénomène d'interaction onde-particule est complexe : il dépend de la taille relative de la particule par rapport à la longueur d'onde mais aussi des propriétés diélectriques du matériau constitutif^[18].

Cet effet peut être utilisé pour manipuler des particules en piégeant celle-ci grâce à un gradient de luminance : c'est le principe de la pince optique.

Applications

Physique des plasmas, astrophysique, physique stellaire

Les applications en astrophysique et physique stellaire sont nombreux :

• formation de l'univers, du système solaire, photo-évaporation, formation et évolutions des étoiles (limite d'Eddington, nova, etc.) ;
• évolution à moyen ou long terme des caractéristiques de nuages de particules solides (queue cométaire, effet Poynting-Robertson) ou de petits corps (effet Yarkovsky, effet YORP, paramètres d'accélération non gravitationnelle).

Dans un domaine voisin on retrouve des problèmes analogues (sauf la gravité bien sûr) en physique des plasmas (fusion nucléaire).

Manipulation de particules

Dans les années 1970, on apprend à manipuler des particules au moyen de la force d'origine radiative^[19], y compris pour faire léviter des particules^[20].

Dans les années 1980, on apprend à capturer des atomes^[21], avant de notamment développer des pièges optiques^[22] et manipuler des bactéries et des virus^[23].

Depuis le milieu des années 1980, on utilise — de plus en plus couramment — la pression radiative d’un laser focalisé pour manipuler, déplacer, trier des objets très petits, particules, protéines, cellules, par exemple pour construire des moteurs moléculaires, des nanoconstituants ou manipuler des cellules au moyen de pinces optiques.

Photovoiles

Parmi les usages envisagés par la science-fiction et les techniques d'exploration spatiale, les voiles solaires sont une méthode possible de propulsion spatiale qui utilise comme force motrice la pression radiative exercée par le rayonnement solaire sur une grande voile.

Depuis début 2016, le projet Breakthrough Starshot ambitionne d'utiliser la pression de radiation couplée à une voile optique pour propulser des sondes à une vitesse de 0,2 c à l'aide d'un laser situé sur la terre.

Accélération d'ions ou de protons

À travers la pression de rayonnement d'un laser, il est possible de générer des ions ou protons ayant des énergies élevées (pouvant aller à plus de 2 GeV selon les paramètres) à l'aide de très fines couches de plasma^[24]. Ceci peut également être utilisé dans le domaine médical (par exemple dans le traitement de tumeurs par faisceau d'ions^[25]).

Notes et références

Notes

1. On a choisi de travailler en fréquence. Tout autre choix est possible sans changer autre chose que les valeurs numériques et les unités.

Références

1. Stellar Atmospheres, D. Mihalas (1978), Second edition, W H Freeman & Co.
2. Eddington, A. S., & Eddington, A. S. (1988). The internal constitution of the stars. Cambridge University Press.
3. Chandrasekhar, S. (2013). Radiative transfer. Courier Corporation.
4. Horst Stöcker, Francis Jundt et Georges Guillaume, Toute la Physique : cours, Dunod, 2007, 1190 p. (ISBN 978-2-10-051181-5 et 2-10-051181-5).
5. Eugene Hecht, "Optics", 4e édition (p. 57).
6. (la) Johannes Kepler, De cometis libelli tres. I. Astronomicus, II. Physicus, III. Astrologicus., Augustae Vindelicorum, 1619.
7. (en) James Clerk Maxwell, « A Treatise on Electricity and Magnetism », Clarendon Press, vol. 2,‎ 1973, p. 391-392 (lire en ligne).
8. (it) A. Bartoli, « Il calorico raggiante e il secondo principio di termodinamica », Il Nuovo Cimento, vol. 15, n^o 1,‎ 1884, p. 193-202 (lire en ligne).
9. (de) P. N. Lebedev, « Untersuchungen über die druckräfte des lichtes », Annalen der Physik, vol. 6,‎ 1901, p. 433–458 (lire en ligne).
10. (en) E. Nichols et G. F. Hull, « A Preliminary Communication on the Pressure of Heat and Light Radiation », Physical Review, vol. 13, n^o 5,‎ 1903, p. 307-320.
11. (en) E. Nichols et G. F. Hull, « The Pressure due to Radiation », Physical Review, vol. 17, n^o 1,‎ 1903, p. 26-50.
12. (en) Marlan O. Scully et M. Suhail Zubairy, Quantum Optics, Cambridge University Press, 1997 (ISBN 0-521-43458-0).
13. (en) Gerald C. Pomraning, The Equations of Radiation Hydrodynamics, Pergamon Press, 2010, 288 p. (ISBN 978-0-08-016893-7 et 0-08-016893-0).
14. « Pression de radiation solaire », sur sesp.esep.pro (consulté le 15 mai 2020).
15. Pierre-Yves Bely, Carol Christian et Jean-René Roy, 250 réponses à vos questions sur l'astronomie, Aix-en-Provence, Le gerfaut, 2008, 299 p. (ISBN 978-2-35191-012-2, lire en ligne), p. 62.
16. (en) J. D. Jackson, Classical Electrodynamics, John Wiley & Sons, 1975 (lire en ligne).
17. (en) Alexander G. Voronovich, Wave Scattering from Rough Surfaces, Springer, coll. « Springer Series on Wave Phenomena » (ISBN 978-3-642-97544-8).
18. (en) M. Dienerowitz, M. Mazilu et K. Dholakia, « Optical manipulation of nanoparticles: a review », Journal of Nanophotonics, vol. 2, n^o 021875,‎ 2008 (lire en ligne).
19. (en) A. Ashkin, « Acceleration and Trapping of Particles by Radiation Pressure », Physical Review Letters, vol. 24, n^o 4,‎ 1970, p. 156–159.
20. (en) A. Ashkin et J. M. Dziedzic, « Optical Levitation by Radiation Pressure », Applied Physics Letters, vol. 19, n^o 8,‎ 1971, p. 283–285.
21. (en) A. Ashkin, S. Chu, J. E. Bjorkholm et A. Cable, « Experimental Observation of Optically Trapped Atoms », Physical Review Letters, vol. 57, n^o 3,‎ 1986, p. 314–317.
22. (en) A. Ashkin, « Optical Trapping and Manipulation of Neutral Particles using Laser », Proceedings of the National Academy of Sciences, vol. 94,‎ 1997, p. 4853–4860.
23. (en) A. Ashkin et J. M. Dziedzic, « Optical Trapping and Manipulation of Viruses and Bacteria », Science, vol. 235,‎ 1987, p. 1517–1520.
24. (en) Tim Arniko Meinhold et Naveen Kumar, « Radiation pressure acceleration of protons from structured thin-foil targets », Journal of Plasma Physics, vol. 87, n^o 6,‎ décembre 2021, p. 905870607 (ISSN 0022-3778 et 1469-7807, DOI 10.1017/S0022377821001070, lire en ligne, consulté le 1^er décembre 2021).
25. (en) Victor Malka, Sven Fritzler, Erik Lefebvre et Emmanuel d'Humières, « Practicability of protontherapy using compact laser systems », Medical Physics, vol. 31, n^o 6,‎ 27 mai 2004, p. 1587–1592 (DOI 10.1118/1.1747751, lire en ligne, consulté le 1^er décembre 2021).

Bibliographie

• (en) Jerome L. Wright, Space Sailing, Gordon et Breach Science Publishers, 1992, 258 p. (ISBN 2-88124-803-9, lire en ligne).
• (pl) Czesław Białobrzeski, La thermodynamique des étoiles, 1931.

• Portail de l’astronomie
• Portail de la physique