Effet papillon

« Effet papillon » est une expression qui résume une métaphore concernant le phénomène fondamental de sensibilité aux conditions initiales de la théorie du chaos. La formulation exacte qui en est à l'origine fut exprimée par Edward Lorenz lors d'une conférence scientifique en 1972, dont le titre était :

« Le battement d'ailes d'un papillon au Brésil peut-il provoquer une tornade au Texas ? »

Un graphique de l'attracteur étrange de Lorenz pour les valeurs ρ = 28, σ = 10, β = 8/3

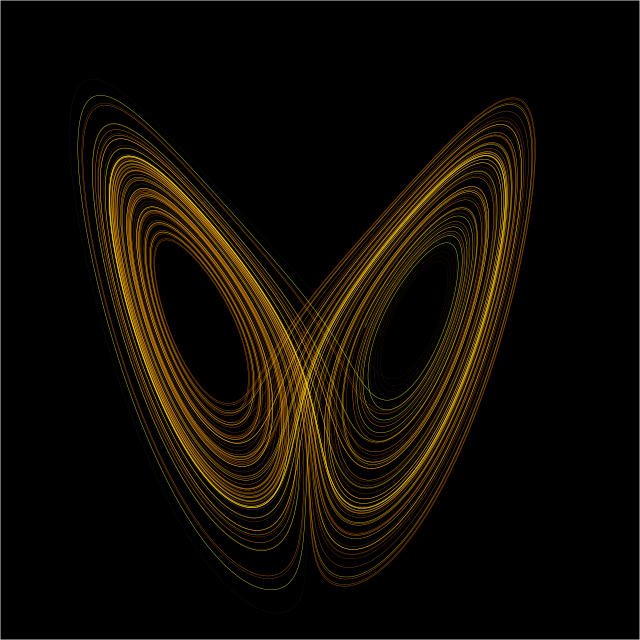
Historique

La contribution de Lorenz

La conférence liminaire

Le battement d'ailes du papillon.

En 1972, le météorologue Edward Lorenz fait une conférence à l'American Association for the Advancement of Science intitulée^[1] : « Predictability: Does the Flap of a Butterfly's Wings in Brazil Set off a Tornado in Texas? », qui se traduit en français par :

« Prédictibilité : le battement d'ailes d'un papillon au Brésil peut-il provoquer une tornade au Texas ? »

Lorenz explique^[2] :

« De crainte que le seul fait de demander, suivant le titre de cet article, « Un battement d'ailes de papillon au Brésil peut-il déclencher une tornade au Texas ? », fasse douter de mon sérieux, sans même parler d'une réponse affirmative, je mettrai cette question en perspective en avançant les deux propositions suivantes :

• Si un seul battement d'ailes d'un papillon peut avoir pour effet le déclenchement d'une tornade, alors, il en va ainsi également de tous les battements précédents et subséquents de ses ailes, comme de ceux de millions d'autres papillons, pour ne pas mentionner les activités d'innombrables créatures plus puissantes, en particulier de notre propre espèce ;
• Si le battement d'ailes d'un papillon peut déclencher une tornade, il peut aussi l'empêcher. Si le battement d'ailes d'un papillon influe sur la formation d'une tornade, il ne va pas de soi que son battement d'ailes soit l'origine même de cette tornade et donc qu'il ait un quelconque pouvoir sur la création ou non de cette dernière. »

Les travaux de Lorenz

Une trajectoire dans l'espace des phases de l'attracteur de Lorenz

Edward Lorenz travaillait sur des problèmes de prédictibilité, à savoir, des prévisions météorologiques grâce à des systèmes informatiques. D’après les lois déterministes — également dites prévisionnistes — créées par Galilée et développées par Isaac Newton selon lequel les conditions initiales permettraient de déterminer l’état futur d’un système grâce à la mise en place d’une nouvelle technique mathématique, le calcul différentiel alors en vigueur, toute action X aurait des conséquences Y prévisibles grâce à des formules mathématiques, pourvu que les fonctions lipschitziennes en cause fussent continûment dérivables (il n’était pas question par exemple de prévoir le mouvement d’un chat par ce moyen). Lorenz a incorporé, en 1963, le fait que des variations infimes entre deux situations initiales pouvaient conduire à des situations finales sans rapport entre elles.

Il affirma ainsi qu’il n’était pas envisageable de prévoir correctement les conditions météorologiques à très long terme (par exemple un an), parce qu’une incertitude de 1 sur 10⁶ lors de la saisie des données de la situation initiale pouvait conduire à une prévision totalement erronée. Or :

• d’une part, ces incertitudes sont inévitables,
• et d’autre part, l’homme ne peut pas prendre en compte tous les éléments qui constituent son environnement, surtout lorsqu’il s’agit de variations infimes.

Les utilisateurs des prédictions météo à 5 jours sur Internet peuvent aujourd'hui se rendre compte de la volatilité des prédictions à mesure de l'écoulement des jours.

Précurseurs

Laplace

Le mathématicien Pierre-Simon de Laplace exprimait le déterminisme en affirmant qu'un génie connaissant exactement la position et le mouvement de tous les objets, même infinitésimaux, de l'univers, aurait accès à la connaissance du passé comme du futur de l'univers. Il notait que cette certitude nous était inaccessible et que seul un résultat stochastique pouvait être proposé^[3]. Cette position n'est pas contredite par la théorie du chaos. Ce qu'affirme la théorie du chaos, c'est qu'une déviation très faible sur un paramètre peut avoir une influence importante sur la situation résultante à une date ultérieure.

Poincaré

Un exemple exposé par Poincaré pour illustrer la notion de chaos.

Henri Poincaré travailla plus tard sur des phénomènes chaotiques, en particulier en réfléchissant à la stabilité du système solaire et au problème des trois corps^[4]. Ses travaux n’eurent pas d’applications immédiates, faute de calculateurs électroniques avec lesquels effectuer plusieurs millions ou milliards d’itérations.

Poe

Poe, dans la nouvelle La puissance de la Parole traduite en français par Charles Baudelaire, évoque longuement ce phénomène^{[Lequel ?][5]}.

Conséquences de la théorie du chaos

Le concept

Le double pendule (simulation Algodoo©) illustre un phénomène physique de sensibilité aux conditions initiales

Dans l’exemple de Lorenz, un météorologue ne penserait pas forcément à prendre en compte les variations du courant d’air provoquées par le battement d’ailes d’un papillon. Son idée de « non infaillibilité du système prévisionnel », théorisé sous la forme de « l’effet papillon », rappelle qu’il existe au moins une différence entre le déterminé et le déterminable.

Des travaux récents ont montré que la modélisation de l'atmosphère n'est pas affecté par l'effet papillon, car un effet minime est « noyé » et oublié sans incidence perceptible pour la totalité^[6].

Il n'en est pas moins vrai que de petits facteurs peuvent avoir d'immenses effets. Blaise Pascal l'avait mentionné à propos du nez de Cléopâtre. Le naturaliste Stephen Jay Gould mentionne de même que le processus darwinien n'est que statistique et que si l'on ramenait la planète Terre 65 millions d'années en arrière, à l'identique, faune comme flore suivraient des chemins sans doute aussi différents que ceux du continent africain et de l'île de Madagascar.

En revanche, l'effet papillon n'est pas une fatalité et les travaux de Jacques Laskar montrent que l'orbite de la Terre ne serait pas restée stable pendant plus d'un milliard d'années sans la petite influence gravitationnelle de la Lune, qui aurait stabilisé son orbite et donc assuré qu'elle reste dans la zone « habitable », et empêchant ainsi l'orbite de divaguer en fonction de variations minimes des conditions ab initio.

Résultats de la théorie du chaos

Avec Lorenz, les limites pratiques du modèle de Newton sont mieux perçues, et un nouveau concept de « déterminisme relatif » émerge. Le terme de « théorie du chaos » réapparaît et c’est au début des années 1970 que le monde connaît un engouement pour ce paradigme. On découvre alors deux résultats étonnants :

• Le chaos possède une sorte de signature (voir Nombres de Feigenbaum) ;
• Il peut conduire lui-même à des phénomènes stables. On parle alors d’émergence. On ne pourra en connaître le détail de réalisation, mais les états finaux peuvent être connus sans qu’on sache par quel chemin on y arrivera : c’est une généralisation de la notion d’attracteur déjà posée par Poincaré.

L'Institut de Santa Fe a été créé en 1984 pour tenter d’étudier les conditions par lesquelles, parfois, c’est l’ordre qui émerge du chaos.

Extrapolations à partir de l'effet papillon

L’effet papillon est utilisé comme métaphore de la vie quotidienne ou de l'histoire. Toutefois il faut se méfier du rapprochement entre ces problématiques. En effet, une des Pensées de Blaise Pascal est souvent résumée par la phrase « Le nez de Cléopâtre, s’il eût été plus court, toute la face de la terre aurait changé^[7]. »

Le livre Impostures intellectuelles indique l'erreur qu'il y a à rapprocher ces réflexions de l'effet papillon. Dans le cas de l'effet papillon, la variation forte est due à une modification très faible en valeur relative d'une variable mathématique. Dans le cas de l'Histoire, l'imprévisibilité est due au fait qu'on ne sait pas du tout la mettre en équations. Il n'est donc même pas possible d'affirmer que les différences donnant intuitivement l'impression d'être insignifiantes (clou d'un fer à cheval) donnent lieu à une faible variation d'un argument numérique. Il n'est pas possible de savoir, tant que l'Histoire n'aura pas été mise en équations (ce qui n'est pas forcément possible), si le système d'équations est effectivement chaotique^[8]. En tout cas, à ce point de nos connaissances, la théorie du chaos n'apporte pas plus d'informations supplémentaires sur ces phénomènes que celles qui se trouvaient déjà dans les proverbes.

Aspects culturels

Films

Plusieurs films utilisent l'effet papillon comme point important de l'intrigue, comme titre, ou les deux. On notera cependant la confusion entre la sensibilité aux conditions initiales (ce que Lorenz a décrit) et le fait qu'une cause infime peut avoir de grands effets (ce qui est un énoncé erroné et dénaturé de l'effet papillon).

Films autour de l'effet papillon

• 1984 : Miracles, film de Jim Kouf
• 1985 : Retour vers le futur, film de Robert Zemeckis
• 1987 : Le Hasard (Przypadek), film de Krzysztof Kieślowski
• 1989 : Retour vers le futur 2, film de Robert Zemeckis
• 1990 : Retour vers le futur 3, film de Robert Zemeckis
• 1993 : Un jour sans fin (Groundhog Day), film de Harold Ramis
• 1993 : Jurassic Park, film de Steven Spielberg
• 1995 : L'Effet papillon (El Efecto mariposa), film de Fernando Colomo
• 1998 : Cours, Lola, cours ! (Lola rennt), film de Tom Tykwer
• 2000 : Le Battement d'ailes du papillon, film de Laurent Firode
• 2000 : Amours Chiennes (Amores Perros), film mexicain de Alejandro González Iñárritu
• 2002 : Irréversible, film français de Gaspar Noé
• 2002 : La machine à explorer le temps, film américain de Simon Wells
• 2004 : L'Effet papillon (The Butterfly Effect), film drame-fantastique américain d'Eric Bress et J. Mackye Gruber
• 2005 : Un Coup de Tonnerre (A Sound of Thunder), film fantastique de Peter Hyams d'après la Nouvelle de Ray Bradbury
• 2006 : L'Effet papillon 2 (The Butterfly Effect 2), film drame-fantastique américain de John R. Leonetti
• 2006 : Babel, film drame américain d'Alejandro González Iñárritu
• 2006 : Déjà Vu, film d'action américain de Tony Scott
• 2006 : Chaos, Film policier/Action, réalisé par Tony Giglio
• 2007 : Crimes à Oxford, film d'Álex de la Iglesia
• 2008 : Dasavathaaram, film de science-fiction indien de K. S. Ravikumar
• 2009 : L'Étrange Histoire de Benjamin Button, film de David Fincher
• 2009 : L'Effet papillon 3 (The Butterfly Effect: Revelation), film drame-fantastique américain de Seth Grossman
• 2009 : Mr. Nobody, film de Jaco Van Dormael
• 2009 : Hot Tub Time Machine, est un film américain réalisé par Steve Pink
• 2012 : Cloud Atlas, film de science-fiction germano-américain, écrit, produit et réalisé par Andy et Lana Wachowski et Tom Tykwer.
• 2014 : Projet Almanac, film de science-fiction américain réalisé par Dean Israelite.

 

Séries

Séries autour de l'effet papillon

• 2003 - 2005 : Le Monde de Joan, série américaine créée par Barbara Hall qui met en scène Joan, une jeune fille qui voit Dieu et lui parle. Il lui demande d'effectuer des tâches diverses, pouvant paraître insignifiantes ou absurdes, mais qui se révèlent être, la plupart du temps, positives par effet papillon.
• 2006 : Valérian et Laureline, anime de science-fiction franco-japonaise librement inspirée de la série de bande dessinée française Valérian et Laureline.
• 2008 : Heroes, série américaine créée par Tim Kring : l'épisode 3-02 s'intitule The Butterfly effect.
• 2008 : Dexter, série américaine créée par James Manos Jr. : dans la saison 3, l'épisode 8 s'intitule L'effet papillon. L'épisode évoque entre autres l'effet papillon, mais ce titre est seulement choisi pour la version française ; le titre original de l'épisode s'intitule The damage a man can do.
• 2008 : Insect, série indienne créée par Vikash Mathur ; l'épisode 3 s'appelle ബട്ടർഫ്ലൈ ഇഫക്ട്.
• 2008 : Breaking Bad, série américaine créée par Vince Gilligan ; l'épisode 13 de la saison 2 se nomme Effet papillon.
• 2010 : Fringe (Saison 3, épisode 3) : une affaire porte sur le cas d'un homme qui utilise ses dons mathématiques pour commettre des meurtres par effet papillon.
• 2023 : Vortex : mini-série franco-belge écrite par Franck Thilliez et réalisée par Slimane-Baptiste Berhoun : L'effet papillon est abordé par le personnage principal Ludovic pour parler des changements que ses actions génèrent dans le passé puis par la suite dans son présent.

 

Bandes dessinées

Bandes dessinées autour de l'effet papillon

• La Métaphore du papillon, collection « Grand Angle », Bamboo Édition (2004), polar-suspens en 3 tomes
• La théorie du chaos, Schelle Pierre, collection "Encrages", Éditions Delcourt (2001), essai en 1 tome

 

Musiques

Musique autour de l'effet papillon

• La chanson de Mass Hysteria : L'effet Papillon
• Chanson de Bénabar, "L'Effet papillon" (2008) : "(...) quand le financier s'enrhume ce sont les ouvriers qui toussent (...) c'est très loin la couche d'ozone mais c'est d'ici qu'on la perce (...)". Cependant la chanson est peut-être mal nommée car la plupart des exemples illustrent plutôt l'effet "Action/Réaction".
• Les deux chansons de The Verve, Buttefly sur A Storm In Heaven (en français : une tempête au paradis) et Catching The Butterfly sur Urban Hymns traitent de l'effet papillon.
• Youssoupha - L'effet Papillon extrait de l'album Sur les chemins du retour (2009)
• Steins Gate OST: Butterfly Effect

• Travis Scott, "Butterfly Effect" sur l'album "Astroworld" en 2018.

 

Jeux vidéo

Jeux vidéo autour de l'effet papillon

Ne proposer que des jeux qui parlent explicitement de l'effet papillon ou dans lesquels c'est un mécanisme notable. Ne pas mettre des jeux video "à choix", car dans tous les jeux de ce genre, les petits choix provoquent de grands effets.

• Dans le jeu Until Dawn où les choix du joueur influencent directement l'histoire, l'effet papillon est mentionné dans les temps de chargements et est au cœur du jeu.
• Le jeu Life is Strange est une série interactive de cinq épisodes. Max Caufield, jeune étudiante passionnée de photographie, suit un jour intriguée un papillon éthéré au fond des toilettes de sa faculté. Elle se trouve alors témoin d'une dispute entre un étudiant et sa camarade qui se conclut par la mort de cette dernière, et déclenche involontairement le pouvoir de remonter le temps. Cherchant désormais à apprivoiser sa capacité à changer le cours des événements, Max est sujette à des pertes de connaissance durant lesquelles elle se trouve en proie à la vision d'une immense tornade. Life is Strange est une ode à l'effet papillon, proposant à plusieurs reprises au joueur d'observer les changements conséquents et d'apparence chaotique engendrés par de légers changements de paramètres sur un même environnement de départ. Il rend également hommage au célèbre titre de la conférence de Edward Lorenz en utilisant les figures du papillon et de la tornade.

 

Émissions de télévision

Émissions de télévision autour de l'effet papillon

• L'Effet papillon (émission de télévision) est un magazine de l'actualité internationale proposant chaque semaine une enquête grand format (35 à 55 minutes), de l'actualité très anglée et des portraits diffusé sur CANAL+.