Cercle de Mohr

Le cercle de Mohr est une représentation graphique des états de contrainte à deux dimensions, proposée par Christian Otto Mohr en 1882.

Dans un graphique où l'axe horizontal représente l'amplitude de la contrainte normale et l'axe vertical représente l'amplitude de la contrainte de cisaillement, le cercle de Mohr est le lieu des états de contrainte en un point P lorsque le plan de coupe tourne autour du point P. Il s'agit d'un cercle centré sur l'axe horizontal dont les intersections avec l'axe horizontal correspondent aux deux contraintes principales au point P.

Ce cercle se construit à partir de la connaissance des efforts extérieurs auxquels est soumise la pièce. Il permet de déterminer :

• les directions principales ${\displaystyle ({\vec {x}}_{\mathrm {I} },{\vec {x}}_{\mathrm {II} },{\vec {x}}_{\mathrm {III} })}$, ainsi que les contraintes principales σ_I, σ_II et σ_III ;
• la direction pour laquelle on a la cission τ maximale, qui est donc la direction de rupture probable (l'orientation du faciès de rupture), ainsi que la valeur de cette contrainte.

Problématique

Représentation graphique de l'état de contrainte

Le cercle de Mohr est une représentation graphique de l'état de contrainte. Il permet une résolution graphique de la validation à l'état limite ultime, selon le critère de Tresca (cission maximale). C'est donc une méthode rapide et demandant peu de moyens de calcul par rapport au traitement du tenseur des contraintes, mais ayant une précision limitée par le tracé.

Notons que le cercle de Mohr représente l'état de contrainte en un point donné.

Recherche de la cission maximale

La rupture d'un matériau ductile — c'est le cas de la plupart des métaux à température ambiante pour des vitesses de déformation modérées — se fait toujours en cisaillement : l'effort nécessaire pour « arracher » les atomes est beaucoup plus important que celui nécessaire pour faire glisser les atomes les uns sur les autres (voir Déformation plastique). Pour une sollicitation donnée d'une pièce, il faut donc savoir dans quelle section la cission τ (tau) est maximale.

Construction du cercle de Mohr dans le cas de la traction simple

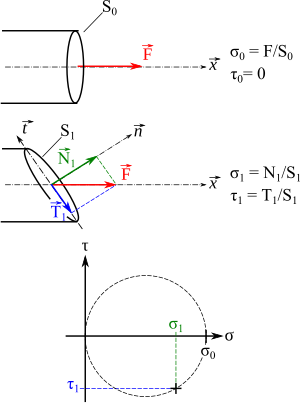
Prenons le cas de la traction simple, ou traction uniaxiale, sur une éprouvette de forme cylindrique. On sait que lors de cet essai, le faciès de rupture va s'amorcer lorsqu'il est orienté à 45° par rapport à l'axe de l'éprouvette. Si l'on considère une section droite de l'éprouvette, celle-ci a une aire S₀ ; la force F que l'on applique est normale à cette section, on a donc une contrainte normale σ₀ qui vaut:

${\displaystyle \sigma _{0}={\frac {\mathrm {F} }{\mathrm {S} _{0}}}}$

et un cisaillement nul.

Considérons une section inclinée d'un angle ${\displaystyle \theta }$ par rapport à la section initiale ; elle a une aire ${\displaystyle S_{1}={\frac {S_{0}}{\cos(\theta )}}}$. Si l'on projette la force ${\displaystyle {\vec {\mathrm {F} }}}$ sur la normale ${\displaystyle {\vec {n}}}$ à cette section, on obtient une force normale ${\displaystyle {\vec {\mathrm {N} }}_{1}}$ de module ${\displaystyle {\mathrm {F} }\cos(\theta )}$. La contrainte normale σ₁ vaut alors:

${\displaystyle \sigma _{1}={\frac {\mathrm {N} _{1}}{\mathrm {S} _{1}}}=\cos(\theta )^{2}\sigma _{0}={\frac {1+\cos(2\theta )}{2}}\sigma _{0}}$.

Si l'on projette ${\displaystyle {\vec {\mathrm {F} }}}$ sur la section, on obtient une force ${\displaystyle {\vec {\mathrm {T} }}_{1}}$ de module ${\displaystyle {\mathrm {F} }\sin(\theta )}$. La cission τ₁ vaut alors:

${\displaystyle \tau _{1}={\frac {\mathrm {T} _{1}}{\mathrm {S} _{1}}}=\cos(\theta )\sin(\theta )\sigma _{0}={\frac {\sin(2\theta )}{2}}\sigma _{0}}$.

Plus la section est inclinée, plus T est grand, mais plus S est grand. Le rapport τ = T/S présente un maximum pour une section située à 45°, ce qui explique le faciès de rupture.

Si maintenant on trace la courbe paramétrée (σ, τ) lorsque ${\displaystyle \theta }$ varie, on voit que l'on obtient un cercle de diamètre ${\displaystyle \sigma _{0}}$ passant par l'origine, le cercle de Mohr.

Les faciès de rupture sur les essais uniaxiaux (traction ou compression) mettent en évidence cette direction de cission maximale à 45°.

• 
  Rupture en traction d'une éprouvette en aluminium de 8 mm de diamètre, avec plan de rupture à 45°
• 
  Rupture en traction d'une éprouvette en acier de section rectangulaire 10 mm×3 mm, avec plan de rupture à 45°
• 
  Rupture en compression d'une éprouvette en béton ; le plan de rupture n'est pas à 45°, en raison du frottement intergranulaire

Tracé du cercle pour des contraintes planes

Cas général

Cercle de Mohr en état de contraintes planes.

Considérons un point P d'un solide ayant un état de contrainte plane. Il s'agit typiquement d'un point de la surface d'une pièce où aucune force extérieure ne s'applique : pas de pression hydrostatique, pas de contact avec une autre pièce (surface libre).

Nous supposons ici que l'on est dans un état de contraintes planes dans le plan (x,y). Le tenseur des contraintes est donc symétrique et de la forme

${\displaystyle {\bar {\bar {\sigma }}}={\begin{pmatrix}\sigma _{x}&\tau _{xy}&0\\\tau _{yx}&\sigma _{y}&0\\0&0&0\end{pmatrix}}}$

avec :

• σ_x : contrainte normale sur la face normale à l'axe x ;
• σ_y : contrainte normale sur la face normale à l'axe y ;
• τ_xy = τ_yx : contrainte de cisaillement sur la face normale à l'axe z.

Considérons un vecteur unitaire ${\displaystyle {\vec {n}}}$ dans le plan (x,y). La contrainte appliquée en P sur une face perpendiculaire à ce vecteur est ${\displaystyle {\bar {\bar {\sigma }}}\,{\vec {n}}}$. Elle admet une composante ${\displaystyle \sigma _{n}}$ colinéaire à ${\displaystyle {\vec {n}}}$ et une composante ${\displaystyle \tau _{n}}$ orthogonale à ${\displaystyle {\vec {n}}}$. L'ensemble des couples ${\displaystyle (\sigma _{n},\tau _{n})}$ lorsque ${\displaystyle {\vec {n}}}$ tourne dans le plan (x,y) décrit un cercle qui est le cercle de Mohr cherché. Ce cercle admet pour diamètre le segment [AB] où :

• le point A décrit les contraintes sur la face normale à x. Il a pour coordonnées (σ_x, τ_xy) ;
• le point B décrit les contraintes sur la face normale à y. Il a pour coordonnées (σ_y, -τ_xy).

ce qui permet de le construire facilement. Les propriétés de ce cercle sont les suivantes :

• Le cercle a donc pour centre le milieu de [AB], d'abscisse C_z = (σ_x + σ_y)/2. Si A et B ne sont pas sur l'axe horizontal, le centre est à l'intersection de [AB] et de l'axe σ_n.
• Le rayon du cercle vaut : ${\displaystyle \mathrm {R} _{z}={\frac {\mathrm {AB} }{2}}={\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}}$ et ce rayon est égal à la cission maximale τ_max.
• Les abscisses des intersections du cercle avec l'axe ${\displaystyle \sigma _{n}}$ valent ${\displaystyle {\frac {\sigma _{x}+\sigma _{y}}{2}}\pm R_{z}}$ et sont égales aux contraintes principales ${\displaystyle \sigma _{\rm {I}}}$ et ${\displaystyle \sigma _{\rm {II}}}$.
• Si l'on veut connaître les contraintes relatives à un vecteur ${\displaystyle {\vec {n}}}$ faisant un angle θ avec l'axe des x dans le plan (x, y ), il faut prendre les coordonnées du point C situé à un angle -2θ du point A sur le cercle (i.e. l'angle ${\displaystyle ({\overrightarrow {\mathrm {OA} }},{\overrightarrow {\mathrm {OC} }})}$ vaut -2θ).
• Si l'on appelle -2θ_p l'angle que fait l'horizontale avec le point A (i.e. ${\displaystyle ({\overrightarrow {\mathrm {OA} }},\sigma _{\mathrm {n} })=-2\theta _{\mathrm {p} }}$), la direction première principale est donné par le vecteur ${\displaystyle {\vec {n}}}$ qui fait un angle θ_p avec l'axe des x, la seconde direction principale lui est perpendiculaire. L'axe σ_n correspond à ces directions principales et l'axe τ_n représente les directions de cission maximale ; les axes géométriques x et y sont représentés par le diamètre [AB].

Démonstration

Soit ${\displaystyle {\begin{pmatrix}\cos(\theta )\\\sin(\theta )\end{pmatrix}}}$ les composantes du vecteur ${\displaystyle {\vec {n}}}$ dans le plan (x,y). Les composantes de ${\displaystyle {\bar {\bar {\sigma }}}\,{\vec {n}}}$ dans ce même plan sont ${\displaystyle {\begin{pmatrix}\cos(\theta )\sigma _{x}+\sin(\theta )\tau _{xy}\\\cos(\theta )\tau _{xy}+\sin(\theta )\sigma _{y}\end{pmatrix}}}$.

La composante ${\displaystyle \sigma _{n}}$ de ce vecteur selon le vecteur ${\displaystyle {\vec {n}}}$ est égal à son produit scalaire par ${\displaystyle {\vec {n}}}$ :

${\displaystyle \sigma _{n}={\vec {n}}\cdot {\bar {\bar {\sigma }}}\,{\vec {n}}=\cos(\theta )^{2}\sigma _{x}+2\cos(\theta )\sin(\theta )\tau _{xy}+\sin(\theta )^{2}\sigma _{y}={\frac {\sigma _{x}+\sigma _{y}}{2}}+\cos(2\theta ){\frac {\sigma _{x}-\sigma _{y}}{2}}+\sin(2\theta )\tau _{xy}}$

Sa composante ${\displaystyle \tau _{n}}$ orthogonale à ${\displaystyle {\vec {n}}}$ est égale au produit scalaire de ${\displaystyle {\bar {\bar {\sigma }}}\,{\vec {n}}}$ par le vecteur de composantes ${\displaystyle {\begin{pmatrix}-\sin(\theta )\\\cos(\theta )\end{pmatrix}}}$, qui est directement orthogonal à ${\displaystyle {\vec {n}}}$, ce qui donne :

${\displaystyle \tau _{n}=\sin(\theta )\cos(\theta )(\sigma _{y}-\sigma _{x})-\sin(\theta )^{2}\tau _{xy}+\cos(\theta )^{2}\tau _{xy}=\sin(2\theta ){\frac {\sigma _{y}-\sigma _{x}}{2}}+\cos(2\theta )\tau _{xy}}$

On obtient le point A pour ${\displaystyle \theta =0\;{\rm {mod}}\;\pi }$, et le point B pour ${\displaystyle \theta =\pm {\frac {\pi }{2}}}$.

Posons ${\displaystyle \mathrm {R} _{z}={\sqrt {\left({\frac {\sigma _{x}-\sigma _{y}}{2}}\right)^{2}+\tau _{xy}^{2}}}}$, et soit ${\displaystyle \theta _{\rm {P}}}$ l'angle tel que ${\displaystyle \cos(2\theta _{\rm {P}})={\frac {\sigma _{x}-\sigma _{y}}{2\mathrm {R} _{z}}}}$ et ${\displaystyle \sin(2\theta _{\rm {P}})={\frac {\tau _{xy}}{\mathrm {R} _{z}}}}$. On obtient alors :

${\displaystyle \sigma _{n}={\frac {\sigma _{x}+\sigma _{y}}{2}}+\mathrm {R} _{z}(\cos(2\theta )\cos(2\theta _{\rm {P}})+\sin(2\theta )\sin(2\theta _{\rm {P}}))={\frac {\sigma _{x}+\sigma _{y}}{2}}+\mathrm {R} _{z}\cos(2\theta _{\rm {P}}-2\theta )}$

${\displaystyle \tau _{n}=\mathrm {R} _{z}(-\sin(2\theta )\cos(2\theta _{\rm {P}})+\cos(2\theta )\sin(2\theta _{\rm {P}}))=\mathrm {R} _{z}\sin(2\theta _{\rm {P}}-2\theta )}$

On voit donc que, lorsque ${\displaystyle \theta }$ varie, le point de coordonnées ${\displaystyle (\sigma _{n},\tau _{n})}$ décrit le cercle de centre O de coordonnées ${\displaystyle ({\frac {\sigma _{x}+\sigma _{y}}{2}},0)}$ et de rayon ${\displaystyle \mathrm {R} _{z}}$. [AB] en est l'un des diamètres, et ${\displaystyle 2\theta _{\rm {P}}}$ est l'angle ${\displaystyle (\sigma _{n},{\overrightarrow {\mathrm {OA} }})}$.

Les contraintes principales sont les valeurs propres de ${\displaystyle {\bar {\bar {\sigma }}}}$ et sont racines du polynôme caractéristique ${\displaystyle (X-\sigma _{x})(X-\sigma _{y})-\tau _{xy}^{2}=X^{2}-(\sigma _{x}+\sigma _{y})X+\sigma _{x}\sigma _{y}-\tau _{xy}^{2}}$. Ces deux racines sont bien ${\displaystyle {\frac {\sigma _{x}+\sigma _{y}}{2}}\pm \mathrm {R} _{z}}$. On les obtient sur le cercle de Mohr pour ${\displaystyle \theta =\theta _{\rm {P}}\;{\rm {mod}}\;{\frac {\pi }{2}}}$.

Sollicitation biaxiale

Cercle de Mohr pour un état de contraintes biaxiales.

Le cas général se simplifie si les axes x et y du repère sont choisis de façon à être les directions principales du tenseur de contrainte au point P. Dans ce cas, ${\displaystyle \tau _{xy}}$ est nul et l'état de contrainte est dit biaxial. Il peut s'agir typiquement d'un point à l'air libre d'un réservoir sous pression, ou bien d'un point d'une tôle soumise à deux couples de forces perpendiculaires dans le plan de la tôle.

Les résultats du paragraphe précédent se simplifient comme suit :

• Le cercle admet pour diamètre les points de coordonnées (σ_x, 0) et (σ_y, 0).
• le centre du cercle a pour abscisse (σ_x + σ_y)/2 ;
• le rayon du cercle de Mohr, égal à la cission maximale, vaut (σ_x - σ_y)/2 (en supposant σ_x supérieur à σ_y). Notons que σ_x ou σ_y peuvent être négatives.

On remarque que le cercle dans le cas σ_x = - σ_y est centré à l'origine, et est identique au cercle obtenu dans le cas d'un cisaillement pur avec une cission nominale égale à σ_x. L'état mécanique est donc identique, et donc si la matière est isotrope, l'état de la matière est identique, seule change l'orientation.

Sollicitation uniaxiale

Cercle de Mohr pour un état de contrainte uniaxial.

État d'équilibre uniaxial

Si ${\displaystyle \tau _{xy}=0}$ et ${\displaystyle \sigma _{y}=0}$, on obtient un état de contrainte uniaxiale. Il s'agit typiquement :

• de tout point d'une pièce rectiligne (poutre) subissant une traction ou une compression dans l'axe (couple de forces colinéaires égales et opposées) : tirant, bielle, poutre d'un treillis, d'une éprouvette de traction ou de compression ; on appelle x l'axe des forces ;
• de tout point d'une pièce rectiligne en flexion pure (partie centrale d'une flexion 4 points) ; on appelle x l'axe de la pièce ;
• de tout point de la surface supérieure ou inférieure d'une poutre en flexion simple (flexion 3 points).

C'est le cas de l'exemple traité dans le paragraphe Recherche de la cission maximale. On retrouve les résultats donnés au paragraphe précédent, avec ${\displaystyle \sigma _{y}=0}$ :

• Le cercle de Mohr admet pour diamètre les points de coordonnées (0,0) et (σ_x,0).
• Il est donc tangent à l'axe τ_n. Il se trouve du côté des σ_n positif dans le cas de la traction, et du côté des σ_n négatifs en compression.
• Son centre est au point d'abscisse C_z = σ_x/2.
• Son rayon, égal au cisaillement maximal, vaut τ_max = R_z = σ_x/2 (ou sa valeur absolue si σ_x est négatif).

Cisaillement pur

Cercle de Mohr pour du cisaillement pur.

Le cisaillement pur se rencontre lorsque le tenseur de contrainte est tel que σ_x = σ_y = 0, et τ_xy non nul. C'est le cas d'un tube en torsion, ou d'une pièce cisaillée, mais uniquement sur le plan à la fibre neutre (le cisaillement simple s'accompagne d'une légère flexion).

Le cercle de Mohr vérifie alors :

• Son centre est l'origine, C_z = 0.
• La contrainte de cisaillement maximale, égale à son rayon, est également la cission nominale τ_xy : τ_max = R_z = τ_xy.
• Les directions principales sont les bissectrices du repère (x,y) (droite à 45° dans l'espace réel), avec σ_I = -σ_II = τ_xy.

Tracé du cercle pour des sollicitations triaxiales

Cas simplifié

L'état de contrainte au point P est dit triaxial lorsque le tenseur de contraintes est diagonal, avec des termes diagonaux non nuls. C'est typiquement un point d'un solide soumis à une pression hydrostatique ou lithostatique, et à une traction ou compression. L'essai triaxial est un essai pratiqué sur des sols (géotechnique).

Le tenseur des contraintes est de la forme

${\displaystyle {\bar {\bar {\sigma }}}={\begin{pmatrix}\sigma _{x}&0&0\\&\sigma _{y}&0\\&&\sigma _{z}\end{pmatrix}}}$.

et l'on suppose que σ_x ≥ σ_y ≥ σ_z. Si l'on considère une surface de normale ${\displaystyle {\vec {n}}(n_{x},n_{y},n_{z})}$, alors le vecteur contraintes vaut

${\displaystyle {\vec {\mathrm {T} }}_{\vec {n}}={\bar {\bar {\sigma }}}\;{\vec {n}}={\begin{pmatrix}\sigma _{x}n_{x}\\\sigma _{y}n_{y}\\\sigma _{z}n_{z}\end{pmatrix}}}$

ayant pour composantes :

• la contrainte normale ${\displaystyle \sigma }$ est la composante de ${\displaystyle {\vec {\mathrm {T} }}_{\vec {n}}}$ selon le vecteur ${\displaystyle {\vec {n}}}$ : ${\displaystyle \sigma ={\vec {n}}\cdot {\vec {\mathrm {T} }}_{\vec {n}}={\vec {n}}\cdot {\bar {\bar {\sigma }}}\;{\vec {n}}=\sigma _{x}n_{x}^{2}+\sigma _{y}n_{y}^{2}+\sigma _{z}n_{z}^{2}}$ ;
• la composante tangentielle ${\displaystyle \tau }$ est obtenue par le théorème de Pythagore : ${\displaystyle \|{\vec {\mathrm {T} }}({\vec {n}})\|^{2}=\sigma ^{2}+\tau ^{2}}$, soit ${\displaystyle \sigma _{x}^{2}n_{x}^{2}+\sigma _{y}^{2}n_{y}^{2}+\sigma _{z}^{2}n_{z}^{2}=\sigma ^{2}+\tau ^{2}}$.

Si l'on ajoute le fait que le vecteur ${\displaystyle {\vec {n}}}$ est un vecteur unitaire, on a un système de trois équations dont on considèrera que les trois inconnues sont n_x², n_y² et n_z² :

${\displaystyle \left\{{\begin{aligned}n_{x}^{2}+n_{y}^{2}+n_{z}^{2}=\ &1\\\sigma _{x}n_{x}^{2}+\sigma _{y}n_{y}^{2}+\sigma _{z}n_{z}^{2}=\ &\sigma \\\sigma _{x}^{2}n_{x}^{2}+\sigma _{y}^{2}n_{y}^{2}+\sigma _{z}^{2}n_{z}^{2}=\ &\sigma ^{2}+\tau ^{2}\\\end{aligned}}\right.}$

dont le déterminant vaut (Matrice de Vandermonde):

${\displaystyle {\begin{vmatrix}1&1&1\\\sigma _{x}&\sigma _{y}&\sigma _{z}\\\sigma _{x}^{2}&\sigma _{y}^{2}&\sigma _{z}^{2}\\\end{vmatrix}}=(\sigma _{x}-\sigma _{y})(\sigma _{y}-\sigma _{z})(\sigma _{z}-\sigma _{x})}$

La résolution de ce système (règle de Cramer) donne :

${\displaystyle \left\{{\begin{aligned}n_{x}^{2}=\ &{\frac {\tau ^{2}+(\sigma -\sigma _{y})(\sigma -\sigma _{z})}{(\sigma _{x}-\sigma _{y})(\sigma _{x}-\sigma _{z})}}\\n_{y}^{2}=\ &{\frac {\tau ^{2}+(\sigma -\sigma _{z})(\sigma -\sigma _{x})}{(\sigma _{y}-\sigma _{z})(\sigma _{y}-\sigma _{x})}}\\n_{z}^{2}=\ &{\frac {\tau ^{2}+(\sigma -\sigma _{x})(\sigma -\sigma _{y})}{(\sigma _{z}-\sigma _{x})(\sigma _{z}-\sigma _{y})}}\\\end{aligned}}\right.}$

Posons :

• C_x = (σ_y + σ_z)/2, R_x = (σ_y - σ_z)/2 ;
• C_y = (σ_x + σ_z)/2, R_y = (σ_x - σ_z)/2 ;
• C_z = (σ_x + σ_y)/2, R_z = (σ_x - σ_y)/2.

Le système est alors équivalent à :

${\displaystyle \left\{{\begin{aligned}n_{x}^{2}=\ &{\frac {\tau ^{2}+(\sigma -C_{x})^{2}-R_{x}^{2}}{(\sigma _{x}-\sigma _{y})(\sigma _{x}-\sigma _{z})}}\\n_{y}^{2}=\ &{\frac {\tau ^{2}+(\sigma -C_{y})^{2}-R_{y}^{2}}{(\sigma _{y}-\sigma _{z})(\sigma _{y}-\sigma _{x})}}\\n_{z}^{2}=\ &{\frac {\tau ^{2}+(\sigma -C_{z})^{2}-R_{z}^{2}}{(\sigma _{z}-\sigma _{x})(\sigma _{z}-\sigma _{y})}}\\\end{aligned}}\right.}$

Compte tenu des signes des dénominateurs (celui de la deuxième équation est négatif alors que les deux autres sont positifs), et du fait que les membres des équations sont des carrés positifs ou nuls, on en déduit les trois inéquations :

${\displaystyle \left\{{\begin{aligned}\tau ^{2}+(\sigma -\mathrm {C} _{x})^{2}\geqslant \ &\mathrm {R} _{x}^{2}\\\tau ^{2}+(\sigma -\mathrm {C} _{y})^{2}\leqslant \ &\mathrm {R} _{y}^{2}\\\tau ^{2}+(\sigma -\mathrm {C} _{z})^{2}\geqslant \ &\mathrm {R} _{z}^{2}\\\end{aligned}}\right.}$

« Tricercle de Mohr »

Dans le plan (σ, τ), la représentation des solutions des équations τ² + (σ - C_i)² = R_i² sont des cercles de centre C_i et de rayon R_i. Donc, l'ensemble des valeurs (σ, τ) pour toutes les orientations possibles de ${\displaystyle {\vec {n}}}$ est une surface délimitée par trois cercles.

Cette figure est appelée « tricercle de Mohr », à la fois parce qu'il s'agit de trois cercles de Mohr, mais aussi car elle est semblable à l'arbelos, forme étudiée entre autres par l'homonyme Georg Mohr.

Chacun des cercles est le cercle que l'on aurait si l'on se plaçait dans un contexte de contraintes biaxiales, (σ_y, σ_z), (σ_x, σ_z) et (σ_x, σ_y). Pour tracer le tricercle connaissant σ_x, σ_y et σ_z, on se rapporte donc aux cas précédents.

On remarque que tous les cercles sont tangents deux à deux, et que le plus grand cercle est le cercle de rayon R_y, donc correspondant au plan (x, z ). La cission maximale vaut donc

τ_max = R_y = (σ_x - σ_z)/2.

Généralisation

L'état de contrainte triaxial est en fait l'état général : si l'on a un tenseur des contraintes dont aucune composante n'est nulle

${\displaystyle {\bar {\bar {\sigma }}}={\begin{pmatrix}\sigma _{x}&\tau _{xy}&\tau _{xz}\\&\sigma _{y}&\tau _{yz}\\&&\sigma _{z}\end{pmatrix}}}$

on sait qu'il existe un repère orthonormé, le repère principal, dans lequel le tenseur est de la forme

${\displaystyle {\bar {\bar {\sigma }}}={\begin{pmatrix}\sigma _{\mathrm {I} }&0&0\\&\sigma _{\mathrm {II} }&0\\&&\sigma _{\mathrm {III} }\end{pmatrix}}}$

ce qui nous ramène au cas précédent.

L'état de contrainte triaxial peut venir d'un chargement complexe, mais aussi tout simplement de la forme de la pièce. Par exemple, une éprouvette entaillée utilisée pour un essai Charpy présente un état de contrainte triaxial en fond d'entaille alors qu'elle n'est soumise qu'à de la flexion.

Cas dégénéré

Considérons le cas où σ_II = σ_III. On a :

• C_I = σ_II, R_I = 0 ;
• C_II = C_III = (σ_I + σ_II)/2 ;
• R_II = R_III = (σ_I - σ_II)/2.

On voit que le cercle I se réduit à un point, et que les cercles II et III sont confondus. On a donc un seul cercle, identique au cas biaxial.

Si les trois contraintes principales sont égales, ce cercle se réduit à un point.

Autres cercles de Mohr

De manière analogue, on peut tracer :

• un cercle de Mohr des déformations ;
• dans le cadre de la théorie des plaques, un cercle de Mohr des moments.

Cercle de Mohr des déformations

On obtient le cercle de Mohr des déformations en traçant le diagramme (ε_ii , ε_ij)_{i ≠ j} , ou si l'on préfère utiliser l'écart à l'angle droit γ_ij , le diagramme (ε_ii , ½γ_ij)_{i ≠ j} .

L'axe horizontal du cercle, ε, représente les directions principales. L'axe vertical, ½γ, représente les directions d'angle de glissement maximal.

Ce cercle de Mohr est très utile en extensométrie, pour dépouiller les résultats donnés par une rosette de jauges de déformation.

Cercle de Mohr des moments

Plaque fléchie par une distribution uniforme de moments sur ses côtés

Coupe selon un plan faisant apparaître un moment de torsion

Considérons une plaque mince rectangulaire, subissant deux moments linéiques répartis uniformément: M_x le long de son côté parallèle à l'axe x et M_y le long de son côté parallèle à l'axe y. Ces moments linéiques ont pour unité le newton (N m/m). Ce sont des moments fléchissants (ils créent une flexion).

Si l'on fait une coupe selon un plan faisant un angle α autour de l'axe z, on voit que cette face subit un moment fléchissant, qui courbe la face, et un moment de torsion qui l'incline. En écrivant l'équilibre de cette portion de plaque, on voit que le moment s'exerçant sur la face de coupe peut se décomposer en un vecteur moment normal m_nn , qui crée la torsion (la section tourne dans le plan), et un vecteur moment tangentiel m_nt qui crée la flexion (la plaque se courbe). On se retrouve dans une situation similaire à celle des contraintes normales et tangentielles.

On peut ainsi tracer un diagramme (m_nn , m_nt ) et l'on obtient un cercle. Les intersections de ce cercle avec l'axe m_n donne les sections principales, c'est-à-dire les sections sur lesquelles le moment de torsion est nul.

Voir aussi

Articles connexes

• Critère de plasticité

Liens externes

Animations de l'École des Mines de Nancy :

• Représentation de Mohr pour un état de contraintes uniaxiales
• Représentation de Mohr en mécanique des milieux continus

• Portail de la physique
• Portail des sciences des matériaux