Loading AI tools
De Wikipédia, l'encyclopédie libre
En astronautique un bilan des modifications du vecteur vitesse est une estimation du besoin de changements de vitesse (delta-v) d'une mission spatiale. Ce bilan est la somme des changements de vitesse requis pour effectuer toutes les manœuvres propulsives durant la mission. En tant que donnée de l'équation de Tsiolkovski, le bilan détermine le carburant requis pour un véhicule selon sa masse vide et son système de propulsion.
Le changement de vitesse est une quantité scalaire qui dépend seulement de la trajectoire du véhicule spatial et pas de sa masse. Par exemple le delta-v pour placer un satellite de communication lourd d'une orbite terrestre basse à une orbite géostationnaire est le même que pour un satellite plus léger. De plus le delta-v est une quantité additive contrairement au temps que durent les propulsions, quantité qui diminue au cours de la mission parce que le satellite devient plus léger en consommant son carburant.
Les tableaux de delta-v requis pour aller d'une région spatiale à une autre sont utiles dans la planification des missions spatiales. En absence d'atmosphère le delta-v requis est le même quel que soit le sens du changement d'orbite; en particulier il faut le même effort pour gagner ou perdre de la vitesse. Une atmosphère peut être utilisée pour ralentir un véhicule spatial par aérofreinage.
Un bilan des modifications du vecteur vitesse typique énumère différentes classes de manœuvres, delta-v par manœuvre et le nombre de manœuvres requises sur la durée de vie du véhicule. Le bilan est simplement la somme de tous les delta-v, comme lors d'un bilan financier. En général le delta-v dépend de la position relative des corps entre eux. Donc les fenêtres de lancement sont souvent calculées d'après les diagrammes de côte de porc (porkchop plot en anglais) qui montrent le delta-v en fonction de la date de lancement.
L'équation de Tsiolkovski dit que le delta-v est proportionnel au logarithme du quotient de la masse pleine et vide du véhicule et de l'impulsion spécifique de son moteur fusée. Un but important dans la conception de la trajectoire d'une mission spatiale est de réduire le delta-v requis pour réduire taille et coût de la fusée qui peut amener le véhicule à sa destination.
Le bilan des modifications du vecteur vitesse le plus simple est calculé à partir de l'orbite de transfert de Hohmann qui mène un véhicule d'une orbite circulaire à une autre orbite circulaire coplanaire en passant par une orbite de transfert elliptique. Dans certains cas un transfert bi-elliptique peut donner un delta-v inférieur.

Le transfert devient plus compliqué si les orbites ne sont pas coplanaires. Dans ce cas un delta-v de plus est nécessaire pour changer le plan de l'orbite. Le changement de vitesse requis à l'intersection entre les plans des orbites est en général très haut. Cependant ces changements de plan peuvent être presque gratuits dans certain cas si on peut se servir de l'assistance gravitationnelle des corps célestes[réf. nécessaire]. Dans d'autres cas élever l'altitude de l'apoapside peut réduire le delta-v total parce que le changement de plan s'effectue a une vitesse inférieure.
L'assistance gravitationnelle peut être utilisé pour changer de vitesse. Si un véhicule passe près d'une planète ou d'une lune, il peut prendre (ou donner) de la vitesse orbitale de ce corps relative au soleil ou une planète.
L'effet Oberth peut aussi réduire le delta-v requis considérablement, parce que brûler du carburant à un potentiel énergétique bas (à une haute vitesse) rend la manœuvre plus effective. Donc par exemple le delta-v de l'orbite de transfert Hohmann pour aller de l'orbite terrestre à l'orbite martienne (pour contrer la gravité du soleil) est de plusieurs km par seconde. Mais le carburant requis de l'orbite terrestre basse pour échapper à l'attraction terrestre est beaucoup moins si la manœuvre est effectuée à proximité de la terre que si elle est effectuée à un point sur l'orbite de la terre autour du soleil loin de la terre.
Les transferts à faible énergie sont pratiqués moins souvent. Cela profitent d'effet non linéaires entre les résonances orbitales et choisissent des trajectoires qui passent près des points de Lagrange. Ces transferts durent longtemps mais on besoin de peu de delta-v.
Comme le delta-v dépend des position et mouvement des objets célestes, surtout quand on utilise l'assistance gravitationnelle et l'effet Oberth, le bilan des modifications du vecteur vitesse change avec la date de lancement. Ceci est visualisé dans un diagramme de côte de porc.
Les corrections de trajectoire demandent aussi un peu de carburant. Les systèmes de propulsions ne donne jamais exactement la propulsion requise dans la bonne direction et la navigation introduit une certaine incertitude. Donc un peu de carburant doit être tenu en compte pour corriger les déviation de la trajectoire optimale.

Le delta-v requis pour un vol suborbital est beaucoup moins que pour un vol orbital. Par exemple le delta-v de SpaceShipOne pour atteindre une altitude de 100 km lors du Ansari X Prize était environ 1,4 km/s. Le delta-v pour atteindre la Station spatiale internationale en orbite terrestre basse (300 km à 400 km) est six fois plus, environ 9,4 km/s. Dû à la nature exponentielle de l'équation de Tsiolkovski, la fusée doit être considérablement plus grande.
Le delta-v pour se déplacer à l'intérieur du système Terre-Lune (vitesses en-dessous de la vitesse de libération) est donné en km/s dans le tableau suivant. Ce tableau assume que l'effet Oberth est utilisé avec un système de propulsion chimique à forte poussée.
Un bouclier thermique et l'aérofreinage sont utilisés pour réduire la vitesse de 3,2 km/s lors du retour depuis une orbite terrestre basse. Le bouclier thermique augmente la masse du véhicule, possiblement jusqu'à 15%. Si on utilise pas de bouclier thermique, le nombre plus élevé du tableau compte. La masse du carburant additionnel pour remplacer l'aérofreinage est probablement plus haute que la masse du bouclier thermique. L'inclinaison orbitale de 28 degrés correspond à un lancement depuis le Centre spatial Kennedy.[réf. nécessaire]
| OTB 28 degrés | OTBE | GEO | TLL-1 | TLL-2[1] | TLL-4/5 | Sélénocentrique | Alunissage | Libération | |
|---|---|---|---|---|---|---|---|---|---|
| Terre | 9.3–10 | ||||||||
| Orbite terrestre basse inclinée de 28 degrés | 4.24 | 4.33 | 3.77 | 3.43 | 3.97 | 4.04 | 5.93 | 3.22 | |
| Orbite terrestre basse équatoriale | 4.24 | 3.90 | 3.77 | 3.43 | 3.99 | 4.04 | 5.93 | 3.22 | |
| Orbite géostationnaire | 2.06 | 1.63 | 1.38 | 1.47 | 1.71 | 2.05 | 3.92 | 1.30 | |
| Point de Lagrange Terre-Lune 1 (TLL-1) | 0.77 | 0.77 | 1.38 | 0.14 | 0.33 | 0.64 | 2.52 | 0.14 | |
| Point de Lagrange Terre-Lune 2 (TLL-2) | 0.33 | 0.33 | 1.47 | 0.14 | 0.34 | 0.64 | 2.52 | 0.14 | |
| Point de Lagrange Terre-Lune 4/5 (TLL-4/5) | 0.84 | 0.98 | 1.71 | 0.33 | 0.34 | 0.98 | 2.58 | 0.43 | |
| Orbite sélénocentrique | 0.90 | 0.90 | 2.05 | 0.64 | 0.65 | 0.98 | 1.87 | 1.40 | |
| Alunissage | 2.74 | 2.74 | 3.92 | 2.52 | 2.53 | 2.58 | 1.87 | 2.80 | |
| Vitesse de libération terrestre | 0 | 0 | 1.30 | 0.14 | 0.14 | 0.43 | 1.40 | 2.80 | |
La propulsion électrique spatiale contemporaine donne une poussée faible de l'ordre de milli-newton donc l'effet Oberth n'a pas lieu. Il faut donc plus de delta-v et plus de temps comparé à une propulsion chimique à forte poussée. Néanmoins les coûts peuvent être plus bas grâce à l'impulsion spécifique très haute. Une augmentation de jours à mois peut être acceptable pour les missions habités au sein du système Terre lune, mais pour les vols interplanétaires les différences sont moins significatives donc une propulsion électrique peut s'avérer favorable.
Le tableau si-dessous donne le delta-v en km/s. Normalement les nombres sont les mêmes dans les deux directions, à parts si l'aérofreinage est utilisé comme expliqué plus haut[2].
| Départ | Destination | Delta-v (km/s) |
|---|---|---|
| Orbite terrestre basse | Point de Lagrange Terre-Lune 1 | 7.0 |
| Orbite terrestre basse | Orbite géostationnaire | 6.0 |
| Orbite terrestre basse | Orbite sélénocentrique | 8.0 |
| Orbite terrestre basse | Point de Lagrange Soleil-Terre 1 | 7.4 |
| Orbite terrestre basse | Point de Lagrange Soleil-Terre 2 | 7.4 |
| Point de Lagrange Terre-Lune 1 | Orbite sélénocentrique | 0.60–0.80 |
| Point de Lagrange Terre-Lune 1 | Orbite géostationnaire | 1.4–1.75 |
| Point de Lagrange Terre-Lune 1 | Point de Lagrange Soleil-Terre 2 | 0.30–0.40 |
La station spatiale Lunar Gateway planifiée doit se trouver en orbite sélénocentrique excentrique d'une durée de sept jours (en anglais seven-day near-rectilinear halo orbit (NRHO)). Des véhicules spatiaux lancés de puis la terre devront faire un passage près de la Lune est s'insérer dans l'orbite NRHO pour s'attacher à la station Lunar Gateway à l'apoapside de cette orbite[3].
| Départ | Destination | Delta-v (km/s) |
|---|---|---|
| Orbite terrestre basse | Injection trans-lunaire | 3.20 |
| Injection trans-lunaire | Orbite sélénocentrique polaire | 0.90 |
| Injection trans-lunaire | Lunar Gateway | 0.43 |
| Lunar Gateway | Orbite sélénocentrique polaire | 0.73 |
| Orbite sélénocentrique polaire | Lunar Gateway | 0.73 |
| Lunar Gateway | Terre | 0.41 |
Pour un véhicule spatial a propulsion chimique utilisant l'effet Oberth:
| Départ | Destination | Delta-v (km/s) |
|---|---|---|
| Orbite terrestre basse | Orbite de transfert de Mars | 4.3[4] (valeur typique non minimale) |
| Vitesse de libération terrestre | Orbite de transfert de Mars | 0.6[5] |
| Orbite de transfert de Mars | Orbite de capture de Mars | 0.9[5] |
| Orbite de capture de Mars | Orbite de transfert de Déimos | 0.2[5] |
| Orbite de transfert de Déimos | Surface de Déimos | 0.7[5] |
| Orbite de transfert de Déimos | Orbite de transfert de Phobos | 0.3[5] |
| Orbite de transfert de Phobos | Surface de Phobos | 0.5[5] |
| Orbite de capture de Mars | Orbite aréocentrique | 1.4[5] |
| Orbite aréocentrique | Surface de Mars | 4.1[5] |
| Point de Lagrange Terre-Lune 2 | Orbite de transfert de Mars | <1.0[4] |
| Orbite de transfert de Mars | Orbite aréocentrique | 2.7[4] (valeur typique non minimale) |
| Vitesse de libération terrestre | Objet géocroiseur le plus proche[6] | 0.8–2.0 |
D'après Marsden et Ross:
« The energy levels of the Sun–Earth L1 and L2 points differ from those of the Earth–Moon system by only 50 m/s (as measured by maneuver velocity). »
« Les niveaux d'énergie des points de Lagrange Soleil-Terre 1 et 2 ne diffèrent de ceux du système Terre-Lune que de 50 m/s (mesuré par la vitesse de manœuvre). »
On utilise la formule
(où μ = GM est le paramètre gravitationnel standard du soleil) pour calculer le delta-v en km/s pour arriver à des destinations différentes en partant de la terre. Les orbites sont circulaire et Pluton est a son périapside. Dans le tableau suivant "Delta-v pour entrer en orbite de transfert Hohmann depuis l'orbite terrestre" donne le changement de vecteur vitesse depuis la vitesse orbitale terrestre à la vitesse requise pour entrer en orbite elliptique dont le point opposé est la distance désirée du soleil. La colonne "Delta-v pour quitter la terre à 300 km d'altitude" donne le changement de vecteur vitesse requis depuis une altitude terrestre de 300 km dans un référentiel non-rotatif centrer sur la terre. Cette valeur est obtenue en ajoutant le carré de la vitesse de cette orbite (7,73 km/s, c'est-à-dire la profondeur du puits gravitationnel terrestre à cette altitude) à l'énergie cinétique spécifique. La colonne "Delta-v depuis l'orbite terrestre basse" es simplement la valeur précédente moins 7,73 km/s. Le temps de transit est calculé selon ans.
Le tableau donne le delta-v requis pour atteindre la distance orbitale de chaque planète. À ce moment la vitesse du véhicule spatial relative à la planète est toujours considérable. Pour entrer en orbite autour de la planète, il faut soi employer plus de delta-v ou faire une aérocapture.
| Destination | Rayon d'orbite (au) | Delta-v pour entrer en orbite de transfert Hohmann depuis l'orbite terrestre | Delta-v pour quitter la terre à 300 km d'altitude | Delta-v depuis l'orbite terrestre basse | Temps de transit |
|---|---|---|---|---|---|
| Soleil | 0 | 29.8 | 31.7 | 24.0 | 2.1 mois |
| Mercure | 0.39 | 7.5 | 13.3 | 5.5 | 3.5 mois |
| Vénus | 0.72 | 2.5 | 11.2 | 3.5 | 4.8 mois |
| Mars | 1.52 | 2.9 | 11.3 | 3.6 | 8.5 mois |
| Jupiter | 5.2 | 8.8 | 14.0 | 6.3 | 2.7 ans |
| Saturne | 9.54 | 10.3 | 15.0 | 7.3 | 6.0 ans |
| Uranus | 19.19 | 11.3 | 15.7 | 8.0 | 16.0 ans |
| Neptune | 30.07 | 11.7 | 16.0 | 8.2 | 30.6 ans |
| Pluton | 29.66 (périapside) | 11.6 | 16.0 | 8.2 | 45.5 ans |
| 1 année-lumière | 63,241 | 12.3 | 16.5 | 8.8 | 2.8 M ans |
La sonde New Horizons a quitté la terre avec une vitesse de plus de 16 km/s ce qui est suffisant pour se libérer du système solaire. La sonde a ensuite aussi obtenue une assistance gravitationnelle de Jupiter.
Pour atteindre le soleil il est en fait pas nécessaire de changer le vecteur vitesse de 24 km/s. On peut changer la vitesse de 8,8 km/s pour aller très loin du soleil, ensuite utilisé une valeur négligeable de delta-v pour réduire le moment cinétique à zéro et retomber vers le soleil. Il s'agit du cas spécial de transfert bi-elliptique qui applique deux transferts de Hohmann.
Le tableau ne tient pas en compte les possibilités d'assistance gravitationnelles de la Lune ou d'autres planètes. Par exemple Vénus est la planète la plus facilement accessible pour ensuite atteindre le soleil ou d'autres planètes. La sonde Galileo par exemple est passée une fois près de Vénus et deux fois près de la Terre pour atteindre Jupiter. La sonde Ulysses a utilisé l'assistance gravitationnelle de Jupiter pour atteindre une orbite polaire autour du Soleil.

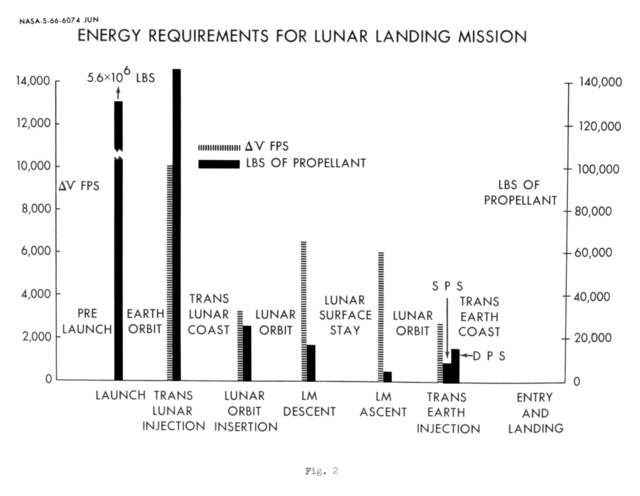
L'image ci-contre donne le delta-v requis pour différentes manœuvres à propulsion conventionnelle[5],[7]. [Note 1]
Les objets géocroiseurs sont des astéroïdes dont l'orbite s'approche jusqu'à 0.3 unités astronomiques de la Terre. Il y a des milliers objets de cette catégorie qu'il est plus facile d'atteindre que la Lune ou Mars. Le delta-v d'aller depuis une orbite terrestre basse est d'environ 3,8 km/s, environ 2/3 du delta-v pour atteindre la surface de la Lune[9]. Les objets géocroiseurs à petit bilan de modification du vecteur vitesse on des longues périodes synodiques et il peut se passer des dizaines d'ans avant qu'une bonne fenêtre de lancement depuis la terre s'ouvre[10],[11].
En général le delta-v pour revenir d'un objet géocroiseur est relativement petit, parfois seulement 60 m/s en utilisant l'atmosphère terrestre pour une aérocapture[9]. Par contre il faut un bouclier thermique qui augmente la masse et affecte la géométrie du véhicule. De plus le phasage peut être problématique, c'est-à-dire qu'un transfert à faible delta-v pour atteindre l'objet géocroiseur va avec une longue attente, au moins un an et souvent plus, pour la fenêtre de retour.
En général les objets plus loin de la Terre ont des fenêtres de lancement plus fréquemment mais demandent plus de delta-v.
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.