Poyntingin teoreema

Poyntingin teoreema on sähkömagneettisen energian säilymislaki, joka on nimetty löytäjänsä John Henry Poyntingin mukaan. Poynting julkaisi teoreeman vuonna 1884. Myös Oliver Heaviside johti vastaavan teoreeman itsenäisesti, mutta julkaisi tuloksensa Poyntingia myöhemmin.^[1] Teoreema on muodoltaan jatkuvuusyhtälö, ja sen mukaan tiettyyn tilavuuteen varastoituneen sähkömagneettisen energian muutos vastaa sähkömagneettisen kentän varausjakaumaan tekemän työn ja tilavuuteen virtaavan energiavuon summaa.

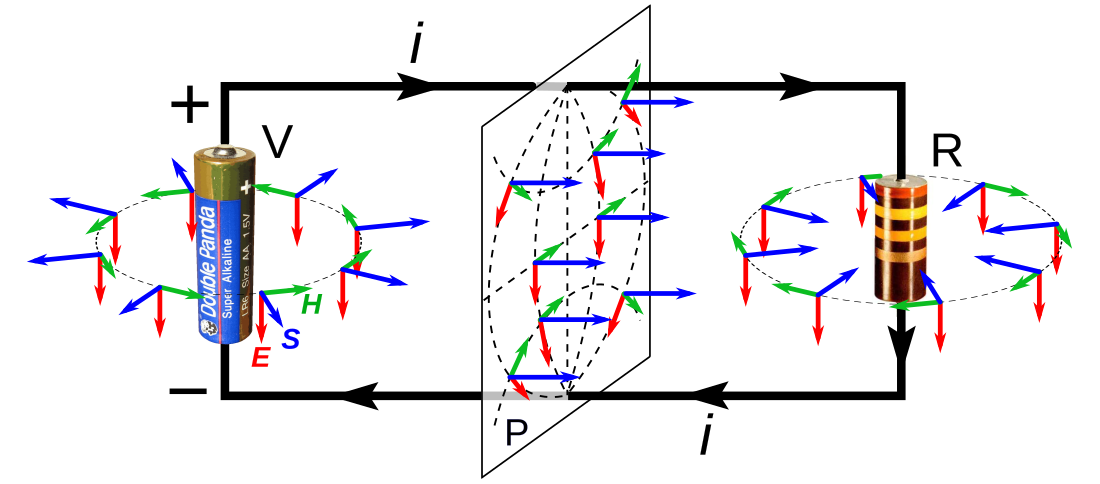
Poyntingin vektori on teoreemassa esiintyvä suure, joka kuvaa sähkömagneettisen kentän energiavuon suuntaa ja suuruutta, eli sähkömagneettisten aaltojen kuljettamaa energiaa pinta-alayksikön läpi yhdessä aikayksikössä. Energiavuon SI-yksikkö on watti per neliömetri (W/m²). Poyntingin vektori saadaan sähkö- ja magneettikenttien tulona, mikä tarkoittaa että sähkö- tai magneettikenttä ei yksinään voi kuljettaa energiaa, vaan siihen tarvitaan molemmat kentät. Sähkömagneettisen tasoaallon Poyntingin vektori osoittaa aallon etenemissuuntaan.

Poyntingin vektorin avulla voidaan esimerkiksi kuvata miten pariston tuottama sähkömagneettinen energia kulkee virtapiirissä paristosta vastukseen, jossa se muuttuu lämpöenergiaksi. Energia ei kulje johtimia pitkin, vaan virtapiiriä ympäröivässä sähkömagneettisessa kentässä.

Poyntingin vektorin avulla voidaan myös kuvata sähkömagneettisen kentän kantamaa liikemäärää, ja erityisesti sen absorption kappaleeseen aiheuttamaa säteilypainetta.

Energiavirrat tasavirtapiirin luomassa sähkömagneettisessa kentässä. Paristo sekä johtimissa ja vastuksessa olevat pintavaraukset synnyttävät piirin ympärille sähkökentän (punainen), ja piirissä kulkeva virta synnyttää sen ympärille magneettikentän (vihreä). Pariston lähellä Poyntingin vektori osoittaa ulospäin paristosta, kun taas vastuksen lähellä se osoittaa vastuksen sisään, niin että pariston energia virtaa sähkömagneettisen kentän kautta vastukseen, jossa se muuttuu lämpöenergiaksi.

Sähkömagneettisen kentän tekemä työ

Sähkömagneettinen kenttä, joka koostuu sähkökentästä ${\displaystyle \mathbf {E} }$ ja magneettikentästä ${\displaystyle \mathbf {B} }$, kohdistaa varausjakaumaan ${\displaystyle \rho }$ Lorentzin voiman

${\displaystyle \mathbf {f} =\rho \mathbf {E} +\mathbf {j} \times \mathbf {B} }$,

missä ${\displaystyle \mathbf {j} =\rho \mathbf {v} }$ on varausjakauman liikkeeseen liittyvä sähkövirran tiheys ja ${\displaystyle \mathbf {v} }$ on varausjakauman nopeutta kuvaava vektorikenttä. Koska magneettikenttä ei tee työtä, yksinkertaistuu sähkömagneettisen kentän varausjakaumaan tekemän mekaanisen työn teho (tilavuuselementtiä kohden) muotoon

${\displaystyle {\frac {dw}{dt}}=\mathbf {j} \cdot \mathbf {E} }$,

Ampèren-Maxwellin lain mukaan sähkövirta vastaa kuitenkin magneettivuon tiheyden roottorin ja sähkökentän aikaderivaatan erotusta, joten teho voidaan kirjoittaa myös muotoon

${\displaystyle {\frac {dw}{dt}}=\left({\frac {1}{\mu _{0}}}\nabla \times \mathbf {B} -\varepsilon _{0}{\frac {\partial \mathbf {E} }{\partial t}}\right)\cdot \mathbf {E} }$,

missä yhtälön oikea puoli ei sisällä suoraa viittausta varausjakaumaan vaan ainoastaan sähkö- ja magneettikenttiin.^[2]

Yllä olevan yhtälön oikea puoli sisältää kaksi termiä, joista jälkimmäinen voidaan kirjoittaa aikaderivaattana, sillä

${\displaystyle \mathbf {E} \cdot {\frac {\partial \mathbf {E} }{\partial t}}={\frac {1}{2}}{\frac {\partial }{\partial t}}|\mathbf {E} |^{2}}$.

Myös ensimmäisestä termistä voidaan erottaa aikaderivaattaa kuvaava osa. Tähän tarvitaan vektori-identiteettiä^[3]

${\displaystyle \mathbf {E} \cdot (\nabla \times \mathbf {B} )=\nabla \cdot (\mathbf {B} \times \mathbf {E} )+\mathbf {B} \cdot (\nabla \times \mathbf {E} )}$.

Saatuun yhtälöön voidaan vielä soveltaa Faradayn lakia, jonka mukaan sähkökentän roottori vastaa magneettikentän aikaderivaattaa.

Näin saadaan Poyntingin teoreeman differentiaalimuoto

${\displaystyle -{\frac {\partial u}{\partial t}}=\nabla \cdot \mathbf {S} +\mathbf {j} \cdot \mathbf {E} }$,

missä yhtälön vasemmalla puolella esiintyvä suure

${\displaystyle u={\frac {\varepsilon _{0}}{2}}\left(|\mathbf {E} |^{2}+c^{2}|\mathbf {B} |^{2}\right)}$,

voidaan tulkita sähkömagneettisen kentän sisältämäksi energiaksi, sillä se on yksinkertaisesti summa sähkö- ja magneettikenttien erikseen sisältämistä energioista.^[2] Yhtälön oikealla puolella esiintyvä suure

${\displaystyle \mathbf {S} ={\frac {1}{\mu _{0}}}\mathbf {E} \times \mathbf {B} }$,

tunnetaan nimellä Poyntingin vektori. Se kuvaa sähkömagneettisen kentän energiavuota. Poyntingin teoreema on energian säilymislain erikoistapaus, joka kuvaa sähkömagneettisen kentän tekemää työtä, ja sitä miten energia virtaa sähkömagneettisessa kentässä.

Koska Poyntingin vektori ei esiinny Poyntingin yhtälössä suoraan vaan ainoastaan divergenssinä ${\displaystyle \nabla \cdot \mathbf {S} }$, voidaan siihen periaatteessa lisätä pyörrevirtoja, jotka voidaan esittää jonkin vektorikentän ${\displaystyle \mathbf {X} }$ roottorina ${\displaystyle \nabla \times \mathbf {X} }$ ja teoreema pysyy voimassa. Yhteensopivuus suhteellisuusteorian periaatteiden kanssa rajoittaa Poyntingin vektorin vapautta, mutta ei poista sitä kokonaan. Poyntingin vektori ei kuitenkaan ole havaittava suure, joten tämä mielivaltaisuus ei ole ongelma.^[2]

Liikemäärä

Sähkömagneettisen säteilykvantin eli fotonin liikemäärä ja energia ovat suoraan verrannollisia toisiinsa:

${\displaystyle p={\frac {E}{c}},}$

missä p on liikemäärän suuruus, E on fotonin energia ja c on valonnopeus. Vastaavasti myös sähkömagneettisen kentän liikemäärätiheys on suoraan verrannollinen Poyntingin vektoriin,

${\displaystyle \mathbf {p} ={\frac {\mathbf {S} }{c}}}$.

Energiavuon lisäksi Poyntingin vektorin avulla voidaan siis kuvailla sähkömagneettiseen kenttään liittyvää liikemäärävuota. Koska sähkömagneettinen säteily kantaa liikemäärää, aiheuttaa sen absorboituminen kappaleeseen säteilypaineen.

Makroskooppiset kentät

Yllä oleva johto on esitetty Maxwellin yhtälöiden mikroskooppisen muotoilun avulla, jossa ei käytetä mitään tiettyä mallia aineen rakenteelle. Poynting itse kuitenkin esitti teoreemansa makroskooppisten kenttien ${\displaystyle \mathbf {D} }$ ja ${\displaystyle \mathbf {H} }$ avulla. Poyntingin vektori saa tällöin muodon

${\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} }$.

Sähkömagneettinen energiavuo koaksiaalikaapelin sisällä. Poyntingin vektori S lasketaan jännitteen V tuottaman sähkökentän E ja sähkövirran I synnyttämän magneettikentän H tulona. Koaksikaapelin ulkopuolella ei ole kenttiä.

Lähteet

1. Lindell, Ismo: Sähkön pitkä historia, s. 197. Gaudemus, 2009. ISBN 978-951-67235-80
2. Andrew Zangwill: Modern electrodynamics. Cambridge. Määritä julkaisija! ISBN 978-0-521-89697-9
3. Feynman, Richard: The Feynman Lectures on Physics, Volume III. Chapter 27. feynmanlectures.caltech.edu. Viitattu 12.1.2022.

Aiheesta muualla

• The Big Misconception About Electricity Veritasium. Viitattu 12.1.2022. (englanti)
• Noah A. Morris, Daniel F. Styer: Visualizing Poynting vector energy flow in electric circuits. American Journal of Physics, 2012-06, nro 80, s. 552–554. doi:10.1119/1.3679838 ISSN 0002-9505 Artikkelin verkkoversio.
• John David Jackson: Classical electrodynamics (3rd ed.), s. 258-267. Wiley, 1999. 38073290 ISBN 978-0-471-30932-1
• I. S. Grant & W. R. Phillips: ”11.4”, Electromagnetism, 2. painos. Wiley, 2003. ISBN 0-471-92712-0

Tämä fysiikkaan liittyvä artikkeli on tynkä. Voit auttaa Wikipediaa laajentamalla artikkelia.