Binäärinen logaritmi

Binäärinen logaritmi eli kaksikantainen logaritmi (log₂ n) on logaritmi, jonka kantaluku on 2. Se on funktion ${\displaystyle y=2^{x}}$ käänteisfunktio ja osoittaa, mihin potenssiin luku 2 on korotettava, jotta saadaan annettu luku. Toisin sanoen:

${\displaystyle y=\log _{2}x\quad \Longleftrightarrow \quad 2^{y}=x.}$

Binäärisen logaritmifunktion y = log₂ x kuvaaja

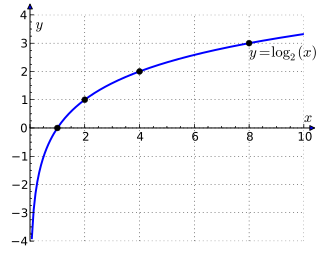
Esimerkiksi luvun 1 binäärinen logaritmi on 0, luvun 2 binäärinen logaritmi on 1, luvun 4 binäärinen logaritmi on 2, luvun 8 binäärinen logaritmi on 3 ja luvun 16 binäärinen logaritmi 4.

Binäärinen logaritmi liittyy läheisesti binääri­luku­järjestelmään. Historiallisesti ensimmäinen binäärisen logaritmin sovellusala oli kuitenkin musiikin teoria, johon sitä sovelsi Leonhard Euler. Muita aloja, joissa binääristä logaritmia paljon käytetään, ovat informaatioteoria, kombinatoriikka, tietojenkäsittelytiede, bioinformatiikka, urheilukilpailujen suunnittelu ja valokuvaus.

Historia

Leonhard Euler oli vuonna 1739 ensimmäinen, joka sovelsi binääristä logaritmia musiikin teoriaan.

Michael Stifel julkaisi vuonna 1544 kahden potensseista taulukon, jota voidaan sen rivit kääntämällä käyttää myös binääristen logaritmien taulukkona.^[1] Binääristen logaritmien sovellukset musiikin teoriassa esitti Leonhard Euler vuonna 1739, kauan ennen kuin nyky­aikainen informaatio­teoria ja tietojen­käsittely­tiede saivat alkunsa. Osana tätä alaa koskevasta tutkimuksestaan Euler laati taulukon kokonaislukujen 1...8 binäärisistä logaritmeista seitsemän desimaalin tarkkuudella.^[2][3]

Merkintätavat

Matematiikassa luvun n binäärinen logaritmi merkitään log₂ n. Varsinkin sovellusaloilla sille kuitenkin käytetään tai on ehdotettu useita muitakin merkintätapoja.

Joskus binääriselle logaritmille käytetään merkintää lg n.^[4][5] Donald Knuth on väittänyt tätä merkintää Edward Reingoldin keksimäksi,^[6] mutta sitä on käytetty sekä informaatio­teoriassa että tietojen­käsittely­tieteessä jo ennen Reingoldia.^[7][8] Joissakin teoksissa binäärinen logaritmi on merkitty myös log n, sen jälkeen kun on sanottu, että jäljempänä logaritmien oletuskantaluku on 2.^[9][10][11]

Toinen varsinkin saksankielisessä kirjallisuudessa usein esiintyvä merkintä samalle funktiolle on ld n, joka tulee sen latinalaisesta nimityksestä logarithmus duālis.^[12] ISO:n standardien ISO 31-11 ja ISO 80000-2 mukaan se tulisi merkitä lb n; kun taas lg n merkitsee luvun n kymmenkantaista eli Briggsin logaritmia log₁₀ n. Tämä ISO:n suosittelema binäärisen logaritmin merkintä ei kuitenkaan ole tullut yleiseen käyttöön.

Sovelluksia

Informaatioteoria

Numeroiden (bittien) lukumäärä positiivisen kokonaisluvun n binääriesityksessä on luvun n binäärisen logaritmin kokonaisosa lisättynä yhdellä, toisin sanoen^[5]

${\displaystyle \lfloor \log _{2}n\rfloor +1.\,}$

Informaatioteoriassa informaatiosisällön ja informaatioentropian määritelmät esitetään usein binäärisen logaritmin avulla, mikä vastaa bitin merkitystä informaation perusyksikkönä. Joskus ne kuitenkin määritellään luonnollisen logaritmin avulla, jolloin informaation yksikkönä on nat.^[13]

Kombinatoriikka

16 pelaajan turnausta esittävä kaavio, jolla on binääripuun rakenne. Puun korkeus (kierrosten määrä turnauksessa) on sama kuin pelaajien lukumäärän binäärinen logaritmi, jos pelaajien lukumäärä on kahden potenssi, muussa tapauksessa suurempi.

Vaikka luonnollinen logaritmi on binääristä logaritmia tärkeämpi monilla puhtaan matematiikan aloilla kuten lukuteoriassa ja matemaattisessa analyysissä, binäärisellä logaritmilla on useita sovelluksia kombinatoriikassa:

• Jokaisen binääripuun, jossa on n lehteä, korkeus on ${\displaystyle \log _{2}n}$, ja se on tasan 2, jos n on kahden potenssi.^[14]
• Jokaisen sellaisen joukkoperheen unionissa, johon sisältyy n eri joukkoa, on vähintään ${\displaystyle \log _{2}n}$ alkiota, ja niitä on tasan ${\displaystyle \log _{2}n}$, jos joukkoperhe on potenssijoukko.
• Jokaisen sellaisen osittaiskuution isometrinen dimensio, jossa on n kärkeä, on vähintään ${\displaystyle \log _{2}n}$, ja sillä on enintään ${\displaystyle {\frac {1}{2}}n\log _{2}n}$ kärkeä, tasan näin monta silloin, kun osittaiskuutio on hyperkuutiograafi.^[15]

Laskennallinen monimutkaisuus

Binäärihaku järjestetyssä taulukossa on algoritmi, jonka ajallinen monimutkaisuus on laskettavissa binäärisillä logaritmeilla.

Binäärinen logaritmi esiintyy usein myös algoritmien analyysissä,^[11] ei vain siksi, koska niissä usein käytetään binäärilukujen aritmetiikkaan, vaan myös koska binäärisiin logaritmeihin päädytään analysoitaessa kahtia haarautuvia algoritmeja.^[6] Jos tehtävällä on alun perin n ajateltavissa olevaa ratkaisua ja joka kerta, kun algoritmin tietty osa toistetaan, mahdollisuuksien lukumäärä puoliintuu, toistojen lukumäärä yhteen yksikäsitteiseen ratkaisuun päätymiseksi on jälleen log₂ n:n kokonaisosa. Tätä ajatusta käytetään useita algoritmeja ja tietorakenteita analysoitaessa. Esimerkiksi binäärihaussa ratkaistavan tehtävän laajuus puoliintuu jokaisella toistokerralla ja sen vuoksi puolitus on toistettava suunnilleen log₂n, ennen kuin päädytään koon 1 tehtävään, joka ratkeaa helposti vakioajassa. Samaan tapaan sellaisen täydellisesti tasapainotetun binääripuuhaun, jossa on n alkiota, korkeus on log₂ n + 1.

Algoritmien suoritusaika ilmaistaan kuitenkin tavallisesti iso O -merkinnällä, jossa vakiotekijät jätetään pois. Koska log₂ n = (log_k n)/(log_k 2), missä k voi olla mikä tahansa yhtä suurempi luku, algoritmien, jotka voidaan suorittaa ajassa O(log₂ n), voidaan myös sanoa olevan suoritettavissa esimerkiksi ajassa O(log₁₃ n). Logaritmin kantaluku sen tapaisissa lausekkeissa kuin O(log n) tai O(n log n) ei sen vuoksi ole merkityksellinen.^[4] Muissa yhteyksissä logaritmin kantaluku on kuitenkin määritettävä. Esimerkiksi O(2^log₂ n) ei ole sama kuin O(2^ln n), koska edellinen on yhtä kuin O(n) ja jälkimmäinen yhtä kuin O(n^0.6931...).

Algoritmeja, joiden suoritusaika on O(n log n), sanotaan joskus linearitmisiksi.^[16] Joitakin esimerkkejä algoritmeista, joiden suoritusaika on O(log n) tai O(n log n) ovat:

• pikalajittelu keskimääräisessä ajassa ja muut vertailulajittelualgoritmit^[17]
• Haku tasa­painotetusta binäärihakupuusta^[18]
• Potenssiin korotus neliöimällä^[19]
• Pisin kasvava alijono^[20]

Bioinformatiikka

Mikroruudukko, joka kuvaa suunnilleen 8700 geenin sisällön. Näiden geenien suhteelliset informaatiomäärät voidaan ilmoittaa binääristen logaritmien avulla.

Bioinformatiikassa mikro­ruudukoita analysoitaessa geenien sisältämän informaation määriä vertaillaan usein informaatio­määrien suhteen binäärisen logaritmin avulla. Käyttämällä logaritmille kanta­lukua 2 esimerkiksi kaksinkertainen informaatio­sisältö vastaa logaritmien erotusta 1, puoliintunut informaatio­sisältö voidaan ilmaista logaritmien erotuksella -1, ja muuttumattomana pysynyt sisältö logaritmien erotusta 0.^[21] Tällä tavalla saadut datapisteet visualisoidaan usein pistekaaviolla, jossa jompikumpi tai molemmat koordinaattiakselit ovat binäärisiä logaritmisia asteikkoja.

Musiikin teoria

Musiikin teoriassa kahden sävelen välisen havaittavan eron eli intervallin määrittelee niiden taajuuksien suhde. Kun tämä suhde on ilmaistavissa murto­luvulla, jonka osoittaja ja nimittäjä ovat pieniä lukuja, sävelet sointuvat hyvin yhteen eli kyseessä on konsonanssi. Yksin­kertaisin ja tärkein tällainen intervalli on oktaavi, jossa taajuuksien suhde on 2:1. Kaksi säveltä ovat niin monen oktaavin päässä toisistaan kuin niiden taajuuksien suhteen binäärinen logaritmi osoittaa.^[22]

Viritys­järjestelmiä ja muita musiikin teorian piirteitä tutkittaessa tarvitaan usein tarkempia lukuarvoja sävelten korkeuserolle. Tällöin on edullista käyttää intervallille mittaa, joka on tarkempi kuin oktaavi ja joka on logaritmien tavoin additiivinen eikä multi­plika­tiivinen, jollainen taajuuksien suhde on. Toisin sanoen jos sävelet muodostavat nousevan säveljonon, sävelten x ja y sekä sävelten y ja z välisten intervallien mitta­lukujen summan tulisi olla sama kuin sävelten x ja y välisen intervallin mittaluku. Eräs sellainen mitta­yksikkö on sentti, joka on tasa­vireisen puoliaskeleen sadasosa eli 1/1200 oktaavia. Jos sävelten taajuudet ovat f₁ ja f₂, niiden välisen intervallin suuruus sentteinä on^[22]

${\displaystyle \left|1200\log _{2}{\frac {f_{1}}{f_{2}}}\right|.}$

Millioktaavi määritellään muutoin samalla tavalla, mutta kertoimen 1200 sijasta käytetään kerrointa 1000.

Urheilukilpailujen ajoitus

Kilpailupeleissä ja urheilulajeissa, joissa kuhunkin otteluun osallistuu kaksi kilpailijaa tai joukkueita, binäärinen logaritmi ilmoittaa niiden kierrosten lukumäärän, joka pudotuspelissä on käytävä, ennen kuin loppuottelussa selviää koko kilpailun voittaja. Jos esimerkiksi pelaajia on 4, voittajan selvittämiseksi tarvitaan log₂(4) = 2 kierrosta, ja jos joukkueita on 32, kierroksia tarvitaan log₂(32) = 5 ja niin edelleen. Jos pelaajien tai joukkueiden lukumäärä n ei ole kahden potenssi, log₂n on pyöristettävä ylöspäin kokonaisluvuksi, sillä tarvitaan ainakin yksi kierros, johon eivät kaikki jäljellä olevat kilpailijat osallistu. Esimerkiksi log₂(6) on noin 2,585, ylöspäin pyöristettynä 3, mikä osoittaa, että jos kilpailuun osallistuu 6 joukkuetta, joko niistä kaksi ei ole mukana ensimmäisellä kierroksella tai yksi ei osallistu toiselle kierrokselle. Sama lukumäärä kierroksia tarvitaan myös voittajan ratkaisemiseksi sveitsiläisessä järjestelmässä.^[23]

Valokuvaus

Valokuvauksessa valotusarvot mitataan filmiin tai sensoriin osuvan valomäärän binäärisenä logaritmina, mikä perustuu Weberin–Fechnerin lakiin, jonka mukaan ihmisen silmä reagoi valomäärään logaritmisesti. Valotukselle käytetäänkin kaksikantaista logaritmista asteikkoa^[24][25] Täsmällisemmin sanottuna valokuvan valotusarvon on

${\displaystyle \log _{2}{\frac {N^{2}}{t}}}$ missä ${\displaystyle N}$ on linssin valotusaukkoa valotuksen aikana mittaava f-luku ja ${\displaystyle t}$ valotusaika sekunteina.

Binäärisiä logaritmeja käytetään myös densitometriassa, ilmaisemaan suurimman ja pienimmän valo­määrän suhdetta, jolla valoherkkä materiaali tai digitaalinen sensori on käyttö­kelpoinen.^[26]

Binäärisen logaritmin laskenta

TI SR-50, tieteellinen laskin vuodelta 1974. Toisella rivillä ovat ln- ja log-näppäintä; log₂-näppäintä ei ole.

Nykyaikaisissa laskimissa on yleensä näppäimet luonnollisen ja Briggsin logaritmin, mutta ei binäärisen logaritmin laskemiseksi. Näiden avulla voidaan kuitenkin myös binäärinen logaritmi laskea käyttämällä logaritmi­järjestelmien välisiä muunnoskaavoja:^[25][27]

${\displaystyle \log _{2}n={\frac {\ln n}{\ln 2}}={\frac {\log _{10}n}{\log _{10}2}},}$

tai likimäärin

${\displaystyle \log _{2}n\approx 1.442695\ln n\approx 3.321928\log _{10}n.}$

Pyöristys kokonaisluvuksi

Binäärinen logaritmi voidaan muotoilla funktioksi kokonaisluvuilta kokonaisluvuille pyöristämällä se ylös tai alas. Nämä kaksi kokonaislukuarvoista binääristä logaritmia liittyvät toisiinsa seuraavan kaavan välityksellä:

${\displaystyle \lfloor \log _{2}(n)\rfloor =\lceil \log _{2}(n+1)\rceil -1,{\text{ if }}n\geq 1.}$

^[28] Näin laajennettuna funktio liittyy läheisesti etunollien lukumäärään x:n etumerkittömässä binääriesityksessä nlz(x). Määritelmää voidaan laajentaa sopimalla, että ${\displaystyle \lfloor \log _{2}(0)\rfloor =-1}$. Saatu funktio on:

${\displaystyle \lfloor \log _{2}(n)\rfloor =31-\operatorname {nlz} (n).}$^[28]

Kokonaislukuarvoinen binäärinen logaritmi voidaan tulkita syötteen tärkeimmän arvon 1 saaneen bitin järjestysluvuksi, kun numerointi aloitetaan nollasta. Monet laitteistoalustat tukevat etunollien lukumäärän laskemista tai vastaavia laskutoimituksia, joiden avulla voidaan nopeasti määrittää binäärinen logaritmi. Linux-ytimessä ja joissakin libc-ohjelmistokirjaston versioissa funktiot fls ja flsl^[29] laskevat myös binäärisen logaritmin pyöristettynä ylöspäin kokonaisluvuksi, johon lisätään yksi.

Rekursiivinen likiarvon laskenta

Positiivisen reaaliluvun binäärinen logaritmi voidaan laskea kahdessa vaiheessa:^[30]

1. lasketaan sen kokonaisosa, ${\displaystyle \lfloor \log _{2}x\rfloor }$, jota sanotaan logaritmin mantissaksi
2. lasketaan sen kokonaisluvun ylittävä osa, jota sanotaan logaritmin karakteristikaksi.

Kokonaisosan laskenta on suoraviivaista. Jokaista lukua x > 0, kohti on yksi ja vain yksi sellainen kokonaisluku n, että 2ⁿ ≤ x < 2ⁿ⁺¹, tai yhtäpitävästi 1 ≤ 2⁻ⁿx < 2. Logaritmin kokonaisosa on yksinkertaisesti n, ja desimaaliosa on log₂(2⁻ⁿx).^[30] Toisin sanoen:

${\displaystyle \log _{2}x=n+\log _{2}y\quad {\text{where }}y=2^{-n}x{\text{ and }}y\in [1,2)}$

Tuloksen kokonaisluvun ylittävä osa on ${\displaystyle \log _{2}y}$, ja se voidaan laskea rekursiivisesti pelkkien kerto- ja jakolaskujen avulla.^[30] Tämä käy päinsä seuraavasti:

1. Aloitetaan edellä saadusta reaaliluvusta ${\displaystyle y\in [1,2)}$ Jos ${\displaystyle y=1}$, lasku on valmis ja kokonaisluvun ylittävä osa on nolla.
2. Muussa tapauksessa ${\displaystyle y}$ korotetaan toistuvasti neliöön, kunnes tuloksena saadaan ${\displaystyle z\in [2,4)}$. Olkoon ${\displaystyle z\in [2,4)}$.
3. Otetaan molemmista puolista logaritmi ja suoritetaan seuraavat algebralliset toimitukset:

   ${\displaystyle {\begin{aligned}\log _{2}z&=2^{m}\log _{2}y\\\log _{2}y&={\frac {\log _{2}z}{2^{m}}}\\&={\frac {1+\log _{2}(z/2)}{2^{m}}}\\&=2^{-m}+2^{-m}\log _{2}(z/2)\end{aligned}}}$

4. Nyt ${\displaystyle z/2}$ on jälleen reaaliluku välillä ${\displaystyle [1,2)}$. Palataan kohtaan 1 ja lasketaan ${\displaystyle z/2}$ binäärinen logaritmi samalla menetelmällä rekursiivisesti.

Tämän tuloksen osoittavat seuraavat kaavat, joissa ${\displaystyle m_{i}}$ on tarvittavien neliöön korotusten lukumäärä algoritmin i:nnellä rekursiokerralla:

${\displaystyle {\begin{aligned}\log _{2}x&=n+2^{-m_{1}}\left(1+2^{-m_{2}}\left(1+2^{-m_{3}}\left(1+\cdots \right)\right)\right)\\&=n+2^{-m_{1}}+2^{-m_{1}-m_{2}}+2^{-m_{1}-m_{2}-m_{3}}+\cdots \end{aligned}}}$

Siinä erikoistapauksessa, että kokonaisluvun ylittävä osa kohdassa 1 osoittautuu nollaksi, kyseessä on äärellinen sarja, joka päättyy joskus. Muussa tapauksessa kyseessä on päättymätön sarja, joka suppenee, sillä jokainen termi on aidosti pienempi kuin edellinen (sillä jokainen ${\displaystyle m_{i}>0}$). Käytännössä tämä ääretön sarja on katkaistava jossakin kohdassa, jolloin saadaan sopiva likiarvo. Jos sarja katkaistaan i:nnen termin jälkeen, tuloksen virhe on pienempi kuin ${\displaystyle 2^{-(m_{1}+m_{2}+\cdots +m_{i})}}$.

Vaihtoehtoinen algoritmi, joka tuottaa jokaisella toistokerralla yhden bitin lisää käyttämällä vaihto- ja vertailuoperaatiota, on myös mahdollinen.^[31]

Tuki aliohjelmakirjastoissa

C-ohjelmointikielen standardin mukaiseen matemaattisten funktioiden kirjastoon sisältyy funktio log2, joka laskee annetun luvun binäärisen logaritmin. Oletusarvoisesti funktio laskee logaritmin kaksoistarkkuusargumentille, mutta sen jotkin versiot sallivat argumentille yksinkertaisen tarkkuuden tai se voi olla myös long double.^[32]

Käännös suomeksi

Tämä artikkeli tai sen osa on käännetty tai siihen on haettu tietoja muunkielisen Wikipedian artikkelista.
Alkuperäinen artikkeli: en:Binary logarithm

Lähteet

1. Vivian Shaw Groza, Susanne M. Shelley: Precalculus mathematics, s. 182. New York: Holt, Rinehart and Winston, 1972. ISBN 978-0-03-077670-0 Teoksen verkkoversio..
2. Leonhard Euler: ”VII luku, De Variorum Intervallorum Receptis Appelationibus”, Tentamen novae theoriae musicae ex certissismis harmoniae principiis dilucide expositae, s. 102–112. Pietarin akatemia, 1739. Teoksen verkkoversio. (latinaksi)
3. Thomas Tegg: ”Binary logarithms”, London encyclopaedia; or, Universal dictionary of science, art, literature and practical mechanics: comprising a popular view of the present state of knowledge, Volume 4, s. 142–143. Määritä julkaisija! Teoksen verkkoversio..
4. Cormen, Thomas H.; Leiserson, Charles E., Rivest, Ronald L., Stein, Clifford: Introduction to Algorithms (2. painos), s. 34, 53–54. MIT Press ja McGraw-Hill, 2001. ISBN 0-262-03293-7
5. Robert Sedgewick, Kevin Daniel Wayne: Algorithms, s. 185. Addison Wesley Professional, 2011. ISBN 9780321573513 Teoksen verkkoversio..
6. Donald E. Knuth: The Art of Computer Programming, 1. osa: Fundamental Algorithms, 3. painos, s. 11. Addisin-Wesley Professional, 1997. ISBN 9780321635747 p. 11 Teoksen verkkoversio.
7. A note on the information content of graphs. Bull. Math. Biophys., 1956, 18. vsk, nro 2, s. 129–135. doi:10.1007/BF02477836 MR:0077919
8. Computer multiplication and division using binary logarithms. IRE Transactions on Electronic Computers, 1962, nro 4, s. 512–517. doi:10.1109/TEC.1962.5219391
9. Mathematics for Engineers, s. 152. (Lainaus: "Seuraavassa, ellei toisin mainita, merkintä log x tarkoittaa aina x:n kaksikantaista logaritmia.") John Wiley & Sons, 2013. 9781118623336 Teoksen verkkoversio.
10. Thomas M. Cover, Joy A. Thomas: Elements of Information Theory, s. 33. (Lainaus: "Ellei toisin mainita, kaikki logaritmit otetaan kaksikantaisina.") John Wiley & Sons, 2012. 9781118585771 Teoksen verkkoversio.
11. Michael T. Goodrich, Roberto Tamassia: Algorithm Design: Foundations, Analysis, and Internet Examples. John Wiley & Sons, 2002. ”"Yksi tietorakenteiden ja algoritmien analysoinnin mielenkiintoisista ja joskus yllättävistäkin piireistä on se, että logaritmit esiintyvät kutakuinkin kaikkialla. ... Kuten on tapana tietojenkäsittelyä käsittelevässä kirjallisuudessa, jätämme logaritmin kantaluvun b merkitsemättä, kun b = 2.” 23
12. esimerkiksi Friedrich L. Bauer: Origins and Foundations of Computing: In Cooperation with Heinz Nixdorf MuseumsForum, s. 54. Springer Science & Business Media, 2009. 9783642029929 Teoksen verkkoversio..
13. Jan C. A. Van der Lubbe: Information Theory, s. 3. Cambridge University Press, 1997. 9780521467605 Teoksen verkkoversio..
14. Ernst L. Leiss: A Programmer's Companion to Algorithm Analysis, s. 28. CRC Press, 2006. ISBN 9781420011708 Teoksen verkkoversio.
15. The lattice dimension of a graph. European Journal of Combinatorics, 2005, 25. vsk, nro 5, s. 585–592. doi:10.1016/j.ejc.2004.05.001 arXiv:cs.DS/0402028
16. Rodger Sedgewick, Kevin Daniel Wayne: Algorithms, s. 186. Addison-Wesley Professional, 2011. p. 186 Teoksen verkkoversio.
17. Cormen et al., p. 156; Goodrich & Tamassia, p. 238.
18. Cormen et al., p. 276; Goodrich & Tamassia, p. 159.
19. Cormen et al., pp. 879–880; Goodrich & Tamassia, p. 464.
20. Jeff Edmonds: How to Think About Algorithms, s. 302. Cambridge University Press, 2008. ISBN 9781139471756 Teoksen verkkoversio..
21. Helen Causton, John Quackenbush, Alvis Brazma: Microarray Gene Expression Data Analysis: A Beginner's Guide, s. 49–50. John Wiley & Sons, 2009. ISBN 9781444311563 Teoksen verkkoversio..
22. Murray Campbell, Clive Geated: The Musician's Guide to Acoustics, s. 78. Oxford University Press, 1994. ISBN 9780191591679 Teoksen verkkoversio..
23. Robert France: Introduction to Physical Education and Sport Science, s. 282. Cengage Learning, 2008. ISBN 9781418055295 Teoksen verkkoversio..
24. Elizabeth Allen, Sophie Triantaphillodou: The Manual of Photography, s. 228. Taylor & Francis, 2001. ISBN 9780240520377 Teoksen verkkoversio..
25. Phil Davis: Beyond the Zone System, s. 17. CRC Press, 1998. ISBN 9781136092947 Teoksen verkkoversio..
26. Susan Zwerman, Jeffrey A. Okun: Visual Effects Society Handbook: Workflow and Techniques, s. 205. CRC Press, 2012. ISBN 9781136136146 Teoksen verkkoversio..
27. Craig P. Bauer: Secret History: The Story of Cryptology, s. 332. CRC Press, 2013. ISBN 9781466561861 Teoksen verkkoversio..
28. Henry S. Warren Jr.: Hacker's Delight, s. 215. Addison Wesley, 2002. ISBN 978-0-201-91465-8
29. Linux kernel API, fls kernel.org. Viitattu 2.3.2015.
30. A note on base-2 logarithm computations. Proceedings of the IEEE, 1973, 61. vsk, nro 10, s. 1519–1520. doi:10.1109/PROC.1973.9318
31. An algorithm for the computation of binary logarithms. IEEE Transactions on Computers, 1991, 40. vsk, nro 11, s. 1267–1270. doi:10.1109/12.102831
32. ISO/IEC 9899:1999 specification, svu 226, contribution = 7.12.6.10 The log2 functions open-std.org..

Aiheesta muualla

• Binary Logarithm Wolfram Math World. Viitattu 2.3.2015.