نظریه صف

نظریهٔ صَف (به انگلیسی: Queueing theory) به معنی مطالعه ریاضی یک ردیف در حال انتظار یا صف است.^[۱] مدل صف ساخته شده تا بتوان از طریق آن طول صف و زمان انتظار را پیش‌بینی نمود.^[۱] نظریه صف عموماً شاخه ای از تحقیق در عملیات شناخته می‌شود زیرا نتایج معمولاً هنگام تصمیم‌گیری در مورد منابع مورد نیاز برای ارائه خدمات استفاده می‌شوند.

نظریه صف در ابتدا ریشه در تحقیقات ارلانگ دارد. زمانی که او مدل‌هایی را برای توصیف سیستم در شرکت تبادلات تلفنی کپنهاگ که یک شرکت دانمارکی است، انجام می‌داد این نظریه شکل گرفت.^[۱] این ایده‌ها از آن زمان دارای کاربردهایی از جمله مخابرات، مهندسی ترافیک، محاسبات^[۲] و به ویژه در مهندسی صنایع در طراحی کارخانه‌ها، مغازه‌ها، دفاتر و بیمارستان‌ها و همچنین در مدیریت پروژه بوده‌است.^[۳][۴]

بررسی کردن

بررسی «صف بندی» در «صف» به‌طور معمول در زمینه تحقیقات دانشگاهی مشاهده می‌شود. در واقع، یکی از برجسته‌ترین ژورنال‌های این حرفه، سیستم‌های صف است.

گره‌های تک صف

یک صف یا گره دارای صف را می‌توان تقریباً یک جعبه سیاه دانست. مشاغل یا «مشتریان» به صف می‌رسند، احتمالاً مدتی صبر می‌کنند، مدتی پردازش می‌کنند و سپس از صف خارج می‌شوند (شکل ۱ را ببینید).

شکل ۱. یک جعبه سیاه. مشاغل به صف می‌رسند و از آن خارج می‌شوند.

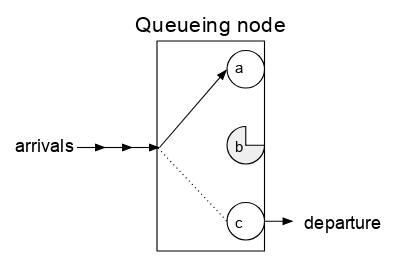
از آنجا که اطلاعاتی در مورد داخل گره دارای صف وجود دارد که باید مشخص کنیم، گره دارای صف کاملاً یک جعبه سیاه خالص نیست. این صف دارای یک یا چند «سرور» است که هر کدام را می‌توان با یک کار ورودی تا زمان ترک آن جفت کرد، و پس از آن آن سرور آزاد خواهد بود که با یک کار ورودی دیگر جفت شود (شکل ۲ را ببینید).

شکل ۲. گره دارای صف با ۳ سرور. سرور a بیکار است و بنابراین برای پردازش ورودی به آن داده می‌شود. سرور b در حال حاضر مشغول است و کمی طول می‌کشد تا سرویس کار خود را کامل کند. سرور c سرویس یک کار را به تازگی به پایان رسانده‌است و بنابراین منتظر برای دریافت کار ورودی بعدی خواهد بود.

تشبیهی که اغلب مورد استفاده قرار می‌گیرد، صندوقدار یک سوپرمارکت است. مدل‌های دیگری نیز وجود دارد، اما این نمونه ای است که در نوشته‌ها معمولاً دیده می‌شود. مشتریان می‌رسند، توسط صندوقدار کارشان انجام می‌شود و می‌روند. هر صندوقدار همزمان کاریک مشتری را انجام می‌دهد و از این رو مشابه یک گره دارای صف است که فقط یک سرور دارد.

تنظیماتی که در صورت مشغول بودن صندوقدار هنگام ورود مشتری، مشتری فوراً آنجا را ترک خواهد کرد، به عنوان صف بدون بافر (یا بدون «منطقه انتظار» یا شرایط مشابه) شناخته می‌شود. و به یک تنظیم با منطقه انتظار برای حداکثر n مشتری، صف با بافر اندازه n گفته می‌شود.

شناخت یک سیستم صف

برای شناختِ یک سیستم صف، باید شش بخش را بشناسیم:

• الگوی ورود مشتریان (کلایِنت)
• الگوی روشِ خدمت‌دهندگان (سِروِرها)
• نظمِ صف
• ظرفیتِ سیستم
• تعدادِ کانالهای سرویس

مشتری و خدمت‌دهنده

در تئوری صف، مشتری واژه‌ای عام است که برای موجودیتی به‌کار می‌رود که برای دریافتِ خدمت، به سیستمی که این خدمت را فراهم می‌کند وارد می‌شود. مکانیزم یا ابزاری که این‌چنین خدمت یا خدماتی را در اختیارِ مشتری قرار می‌دهد، سِروِر یا خدمت‌دهنده نام دارد.

فرایند تولد و مرگ

رفتار / وضعیت یک صف واحد (که " گره صف " نیز نامیده می‌شود) را می‌توان با یک فرایند تولد-مرگ توصیف کرد، که ورود و خروج از صف را در طول تعدادی کار (که متناسب با زمینه استفاده،"مشتری"، "درخواست" یا هر تعداد چیز دیگر، گفته می‌شود) موجود در سیستم، توصیف می‌کند. ورود هر کار، تعداد k را ۱ واحد افزایش می‌دهد و خروج هر کار (کاری در حال تکمیل خدمات خود باشد) k را ۱ واحد کاهش می‌دهد (شکل ۱ را ببینید).

شکل ۳. روند تولد / مرگ. مقادیر موجود در دایره‌ها نشان‌دهنده وضعیت فرایند تولد مرگ برای k فرایند است. انتقال سیستم بین k فرایندها توسط «تولد» و «مرگ» است که به ترتیب با نرخ داده‌شده توسط مقادیر مختلف λ_i و μ_i رخ می‌دهد. برای یک سیستم صف‌بندی، k تعداد کارهای موجود در سیستم (در حال سرویس‌دهی یا در حال انتظار درصورتی‌که صف دارای بافر برای کارهای در حال انتظار باشد) است. بعلاوه، برای یک صف، نرخ ورود و نرخ خروج معمولاً با توجه به تعداد کارهای موجود در صف در نظر گرفته نمی‌شود، بنابراین ما یک نرخ متوسط ورود و خروج در واحد زمان به صف را در نظر می‌گیریم. ازاین‌رو، برای یک صف، این نمودار دارای نرخ ورود λ = λ_{1 ,} λ_{2 ,} … , λ_k، و نرخ خروج µ = µ _{1 ,} µ _{2 ,} … , µ _k است (شکل ۴ را ببینید).

شکل ۱. روند تولد / مرگ. مقادیر موجود در دایره‌ها نشان‌دهنده وضعیت فرایند تولد مرگ برای k فرایند است. انتقال سیستم بین k فرایندها توسط «تولد» و «مرگ» است که به ترتیب با نرخ داده‌شده توسط مقادیر مختلف λ_i و μ_i رخ می‌دهد. برای یک سیستم صف‌بندی، k تعداد کارهای موجود در سیستم (در حال سرویس‌دهی یا در حال انتظار درصورتی‌که صف دارای بافر برای کارهای در حال انتظار باشد) است. بعلاوه، برای یک صف، نرخ ورود و نرخ خروج معمولاً با توجه به تعداد کارهای موجود در صف در نظر گرفته نمی‌شود، بنابراین ما یک نرخ متوسط ورود و خروج در واحد زمان به صف را در نظر می‌گیریم. ازاین‌رو، برای یک صف، این نمودار دارای نرخ ورود λ = λ_{1 ,} λ_{2 ,} … , λ_k، و نرخ خروج µ = µ _{1 ,} µ _{2 ,} … , µ _k است (شکل ۲ را ببینید).

شکل ۴. یک صف با یک سرور، نرخ ورود λ و نرخ خروج μ.

شکل ۲. یک صف با یک سرور، نرخ ورود λ و نرخ خروج μ.

معادلات حالت پایدار برای روند تولد و مرگ به شرح زیر است. (در اینجا p نشان‌دهنده احتمال حالت پایدار در وضعیت n است)

معادلات تعادل

معادله حالت ۱ (از طریق حالت ۰): µ₁P₁ = λ₀P₀

معادله حالت ۲ (از طریق حالت ۱ و ۰): λ₀P₀ + µ₂P₂ = (λ₁+ µ₁)P₁

معادله عمومی (بیان حالت n + 1 از طریق حالت‌های n - 1، n):

از دو معادله اول داریم:

فرمول

با استنتاج ریاضی به فرمول زیر خواهیم رسید:

فرمول

از شرط:

خواهیم داشت:

که برای nهای بزرگتر و مساوی با ۱، به‌طور کامل احتمالات حالت پایدار موردنیاز را توصیف می‌کند.

معیارهای ارزیابی

برای سنجش عملکرد یک سیستم صف از سه معیار زیر بهره می‌گیرند.

• طول صف: طبیعی است که تشکیل صف هزینه زا است. از طرفی سازمان مجبور است فضایی برای انتظار مشتریان قرار دهد (مانند اتاق انتظار). بنابراین تعداد مشتریانی که در صف منتظر دریافت خدمت هستند یا تعداد مشتریان داخل سیستم، معیاری برای ارزیابی سیستم صف محسوب می‌شوند.
• زمان انتظار هر مشتری در صف یا سیستم: رضایت حضور مشتری با میزان حضورش در سیستم رابطه عکس دارد به این معنی که حضور مشتری در صف، هزینه از دست دادن مشتری را به سازمان تحمیل می‌کند؛ بنابراین هزینه زمان انتظار در صف و مدت زمان دریافت سرویس، یکی از معیارهای مهم ارزیابی صف است.
• درصدی از زمان که سیستم به علت نبودن مشتری بیکار است: سازمان برای حضور هر خدمت دهنده در سیستم هزینه‌ای به صورت ثابت یا متغیر تخصیص می‌دهد که جزء هزینه‌های سازمان است؛ بنابراین سازمان علاقه دارد تا درصد بیکاری سرورها را به حداقل ممکن برساند.
  

دقت کنید که اکثر سیستم‌های مورد بررسی، سیستم‌هایی تصادفی هستند و بنابراین مقادیر عددی معیارهای نام برده نیز رفتاری تصادفی دارند؛ بنابراین از ارزش انتظاری یا میانگین این معیارها، به عنوان معیار ارزیابی استفاده می‌شود.

علامت گذاری کندال

برای نمایش سیستم صف معمولاً از شیوه علامت گذاری کندال استفاده می‌شود که به شکل A/S/c توصیف می‌شود که در آن A نوع توزیع زمان بین هر ورود به صف می‌باشد، S نوع توزیع زمان سرویس برای مشتری‌ها را مشخص می‌کند و c نمایانگر تعداد سرورهای بکار رفته در گره می‌باشد.^[۵][۶] برای نشان دادن یک نمونه از علامت گذاری می‌توان صف M/M/1 را که یک مدل ساده است را استفاده کرد، که در اینجا یک سرور به مشتری‌هایی که براساس فرایند پواسون (به صورتی که مدت زمان بین ورود به صورت توزیع نمایی می‌شود) می‌رسند، خدمات دهی می‌کند و دارای مدت زمان‌های انجام سرویس به صورت توزیع نمایی شده‌اند (که M فرایند مارکوف را نشان می‌دهد). در یک صف G ,M/G/1 مخفف واژه General (عمومی) است که یک توزیع احتمال عمومی برای مدت انجام سرویس را نشان می‌دهد.

صف درجه دو ساده

یک سیستم پایه و متداول صف، سیستم صف ارلانگ است که ناشی از تغییر در برخی از قوانین لیتل است. چنانچه در یک صف، نرخ ورود به آن را λ، نرخ خروج از آن را σ و نرخ سرویس دهی μ در نظر بگیریم، طول صف برابر است با:

با فرض توزیع نمایی برای نرخ‌های مذکور، زمان انتظار w را می‌توان نسبت ورودی‌ها به مواردی که سرویس داده می‌شوند، دانست؛ بنابراین، نرخ بقای نمایی آن‌هایی که در طول مدت انتظار، خارج نمی‌شوند به‌صورت زیر است:

معادله دوم معمولاً به‌صورت زیر بازنویسی می‌شود:

این مدل دومرحله‌ای یک جعبه‌ای در اپیدمیولوژی رایج است.^[۷]

مروری بر چگونگی توسعه نظریه صف

در سال ۱۹۰۹، اگنر کراروپ ارلانگ که یک مهندس دانمارکی بود و در یک مرکز تلفن واقع در کپنهاگ کار می‌کرد، اولین مقاله خود را که هم‌اکنون ما آن را تئوری صف می‌نامیم را منتشر کرد.^{[۸][۹][۱۰]} او شماره تلفن‌هایی که جهت تماس به مرکز تبادل (تلفن) می‌رسیدند را بوسیله فرایند پواسون مدل کرد و در سال ۱۹۱۷ صف M/D/1 و در سال ۱۹۲۰ مدل صف M/D/k را حل کرد.^[۱۱] در علامت گذاری کندال:

• M مخفف مارکوف(Markov) یا بدون حافظه است و به این معنی است که ورودها بر اساس فرایند پواسون انجام می‌شود.
• D مخفف ثابت یا قطعی(Deterministic) است و به این معنی است که مشتریانی که وارد صف می‌شوند به چه مقدار مشخصی از خدمت نیاز دارند.
• k نمایانگر تعداد سرورها در گره صف می‌باشد.

اگر تعداد مشتری‌هایی که داریم بیشتر از تعداد سرورهای ما باشد، آن وقت مشتری‌ها به صف خواهند رفت و برای سرویس‌گیری منتظر می‌شوند.

صف M/G/1 در سال ۱۹۳۰ توسط فلیکس پولاچک حل شد،^[۱۲] این راه حل بعداً توسط الکساندر خینچین با اصطلاحات احتمالی اصلاح شد و اکنون به عنوان فرمول پولاچیک - خینچین شناخته می‌شود.^[۱۱][۱۳]

بعد از دهه ۱۹۴۰، تئوری صف به یک زمینه تحقیقاتی جذاب برای ریاضیدانان تبدیل شد.^[۱۳] در سال ۱۹۵۳ دیوید جرج کندال صف GI/M/k را حل کرد^[۱۴] و علامت گذاری مدرن را برای صف‌ها معرفی کرد که اکنون به نام علامت گذاری کندال شناخته می‌شود. در سال ۱۹۵۷ پولاچک از معادله انتگرالی برای مطالعهٔ صف GI/G/1 استفاده کرد.^[۱۵]

جان کینگمن یک فرمول برای محاسبه متوسط زمان انتظار در صف G/G/1 ارائه کرد که به فرمول کینگمن معروف است.^[۱۶]

لئونارد کلین راک بر روی کاربرد تئوری صف روی سوئیچینگ پیام (در اوایل دهه ۱۹۶۰) و سوئیچینگ بسته (در اوایل دهه ۱۹۷۰) کار می‌کرد. سهم اولیه وی در این زمینه، پایان‌نامه دکتری وی در انستیتوی فناوری ماساچوست در سال ۱۹۶۲ بود. که در قالب یک کتاب در زمینه سوئیچینگ پیام در سال ۱۹۶۴ منتشر شد. کارهای نظری او در اوایل دهه ۱۹۷۰ که زیربنای استفاده از سوئیچینگ بسته در ARPANET بود منتشر کرد.

مشکلاتی مانند معیارهای عملکرد برای صف M/G/k جزو مسائلی هستند که هنوز باز هستند.^[۱۱][۱۳]

ترافیک سنگین / تقریب انتشار

در یک سیستم با نرخ بالای اشغال (میزان استفاده نزدیک به ۱) از تقریب ترافیک سنگین می‌توان برای تقریب فرایند طول صف با حرکت براونی معکوس،^[۱۷]فرایند Ornstein Uhlenbeck یا روند انتشار عمومی‌تر استفاده کرد.^[۱۸] تعداد ابعاد RBM برابر با تعداد گره‌های صف‌بندی است و انتشار محدود به orthant غیر منفی است.

محدودیت‌های سیال

مدل‌های سیال، آنالوگ‌های قطعی پیوسته شبکه‌های صف هستند که به اشیا ناهمگن اجازه می‌دهند فرایند با در نظر گرفتن محدودیت زمانی، در زمان و مکان مقیاس بندی شود. این خط مقیاس به یک معادله قطعی همگرا می‌شود که اجازه می‌دهد ثبات سیستم اثبات شود. مشخص‌شده‌است که یک شبکه صف می‌تواند پایدار باشد، اما دارای محدودیت‌های سیال ناپایدار باشد.^[۱۹]

سیاست‌های خدماتی

صف FIFO

سیاست‌های برنامه‌ریزی مختلفی را می‌توان در نودهای صف‌بندی به کار برد:

اولین ورودی / اولین خروجی (FIFO)

این اصطلاح اولین ورودی اول سرویس می‌گیرد (FCFS) نیز نامیده می‌شود،^[۲۰] این اصل بیان می‌کند که مشتریان به‌طور هم‌زمان سرویس دهی می‌شوند و برای مشتری که بیشترین مدت انتظار را داشته‌است ابتدا خدمات ارائه می‌شود.^[۲۱]

آخرین ورودی / اولین خروجی (LIFO)

این اصل همچنین بیان می‌کند که مشتریان به‌طور هم‌زمان سرویس دهی می‌شوند اما برای مشتری با کمترین زمان انتظار ابتدا خدمات ارائه می‌شود.^[۲۱] به عنوان پشته نیز شناخته می‌شود.

اشتراک پردازنده

ظرفیت خدمات به‌طور مساوی بین مشتریان تقسیم می‌شود.^[۲۱]

• اولویت

ابتدا به مشتریانی که اولویت بالایی دارند خدمات ارائه می‌شود.^[۲۱] صف‌های اولویت دار می‌توانند دو نوع باشند، غیر پیشگیرانه (کار در زمان انجام خدمت نمی‌تواند قطع شود) و پیشگیرانه (در صورتی که یک کار در حال خدمت‌گیری است می‌تواند توسط یک کار با اولویت بالاتر قطع شود). هیچ کاری در هر دو مدل از بین نمی‌رود.^[۲۲]

اول کوتاه‌ترین کار

کار بعدی که باید خدمت گیرد کاری با کوچک‌ترین اندازه است.

• اول کوتاهترین کار پیشگیرانه

کار بعدی که باید خدمت گیرد کاری با کوچک‌ترین اندازه اصلی است^[۲۳]

کوتاهترین زمان پردازش باقی مانده

کار بعدی که باید خدمت گیرد کاری با کمترین نیاز پردازش باقی مانده‌است.^[۲۴] ۱)امکانات خدماتی

• سرور منفرد: مشتریان در صف قرار می‌گیرند و فقط یک سرور وجود دارد
• چندین سرور موازی - یک صف: مشتریان در صف قرار می‌گیرند و چندین سرور نیز وجود دارد
• چندین سرور - چند صف: تعداد زیادی شمارنده وجود دارد و مشتریان می‌توانند تصمیم بگیرند که به کجا صف بروند

۲)رفتار مشتری در انتظار

• طفره رفتن: مشتریان تصمیم می‌گیرند اگر صف طولانی باشد به صف ملحق نشوند.
• فریب دادن: اگر مشتریان فکر کنند با این کار سریعتر به آنها سرویس داده می‌شود، بین صف‌ها جابجا می‌شوند.
• انکار کردن: اگر مشتریان بیش از حد منتظر خدمات مانده باشند، صف را ترک می‌کنند.

ورود مشتریانی که به آنها سرویس داده نشده‌است (یا به دلیل صف نداشتن حافظه، یا به دلیل امتناع مشتری) نیز به عنوان از قلم افتادگی شناخته می‌شوند و میانگین نرخ از قلم افتادگی پارامتر قابل توجهی برای توصیف یک صف است.

شبکه‌های صف بندی

شبکه‌های صف به سیستم‌هایی گفته می‌شود که در آن تعدادی از صف‌ها توسط آنچه که به عنوان مسیریابی مشتری شناخته می‌شود متصل می‌شوند. وقتی مشتری در یک گره سرویس دهی می‌شود، می‌تواند به یک‌گره و صف دیگری برای سرویس‌گیری ملحق شود، یا شبکه را ترک کند. برای شبکه‌هایی متشکل از m گره وضعیت سیستم را می‌توان با یک بردار m بعدی (x₁, x₂, … , x_m) توصیف کرد که در آن x_i تعداد مشتریان در هر گره را نشان می‌دهد. ساده‌ترین شبکه غیر بدیهی صف، صف‌های پشت سر هم نامیده می‌شود.^[۲۵] اولین نتایج قابل توجه در این حوزه شبکه‌های جکسون بود،^[۲۶][۲۷] که یک توزیع ثابت از فرم محصول کارآمد وجود دارد. تجزیه و تحلیل مقدار میانگین^[۲۸] به معیارهای میانگین مانند زمان تولید و زمان اقامت اجازه می‌دهد تا محاسبه شود.^[۲۹] اگر تعداد کل مشتریان در شبکه ثابت بماند، شبکه یک شبکه بسته نامیده می‌شود و همچنین که یک توزیع ثابت از محصول در قضیه گوردون-نیول نشان داده شده‌است.^[۳۰] این نتیجه به شبکه BCMPتعمیم داده شد^[۳۱] که در آن یک شبکه با زمان سرویس دهی عمومی، رژیم‌ها و مسیر یابی مشتریان یک توزیع ثابت محصول را نشان می‌دهند. ثابت نرمال سازی را می‌توان با الگوریتم بوزن Buzen، پیشنهاد شده در سال ۱۹۷۳، محاسبه کرد.^[۳۲] شبکه‌های کلی (Kelly) که در آن مشتریان طبقات مختلف سطوح اولویت متفاوتی را در گره‌های خدماتی مختلف تجربه می‌کنند بعنوان شبکه‌های مشتریان مورد بررسی قرار گرفته‌است.^[۳۳] نوع دیگری از شبکه‌ها، شبکه‌های G هستند که برای نخستین بار توسط ارول گلنبه Erol Gelenbe در سال ۱۹۹۳ پیشنهاد شد:^[۳۴] این شبکه‌ها توزیع زمان نمایی شبیه شبکه کلاسیک جکسون ندارند.

الگوریتم‌های مسیریابی

در شبکه‌های زمانی گسسته که در آن محدودیت وجود دارد که گره‌های سرویس می‌توانند در هر زمان فعال باشند، الگوریتم زمان‌بندی حداکثر وزن، یک سیاست خدماتی را انتخاب می‌کند تا بتواند توان عملیاتی مطلوب در شرایطی که برای هر کار فقط از یک گره خدمات شخصی ارائه دهد.^[۲۰] در حالت کلی تر که کارها می‌توانند بیش از یک نود به آن مراجعه کننده داشته باشند، مسیریابی فشار تخلیه backpressure routing توان عملیاتی بهینه را ارائه می‌دهد. یک برنامه‌ریز شبکه باید یک الگوریتم صف بندی را انتخاب کند، که بر ویژگی‌های شبکه‌های بزرگتر تأثیر بگذارد

محدودیت‌های میدانی میانگین

مدلهای میدانی میانگین، محدودیت رفتار اندازه‌گیری تجربی (نسبت صف در حالت‌های مختلف) را در نظر می‌گیرند زیرا تعداد صفها (بیشتر از m) به سمت بی‌نهایت می‌رود. تأثیر صفهای دیگر بر هر صف معین در شبکه با یک معادله دیفرانسیل تقریب زده شود. مدل قطعی به توزیع ایستا مشابه مدل اصلی همگرا می‌شود.^[۳۵]

منابع

• نظریه صف، ژوئیه، فریبرز؛ شامخی امیری، علیرضا
• نظام‌الدین فقیه، مبانی شبیه‌سازی سیستمها ۹۶۴-۶۸۱۰-۰۶-۳:شابک^[۳۶][۳۷]
• نظام‌الدین فقیه، مهندسی تعمیرات و نگهداری^[۳۸][۳۹]