Onda triangular

La onda triangular es una forma de onda periódica que presenta unas velocidades de subida y bajada (Slew Rate) constantes. Lo más habitual es que sea simétrica, es decir que, los tiempos de subida y bajada son iguales.

Una onda triangular de banda limitada, en el dominio del tiempo (arriba) y en el dominio de la frecuencia (abajo). La frecuencia fundamental está en 220 Hz (A₃).

Onda triangular a 220 Hz.

Propiedades

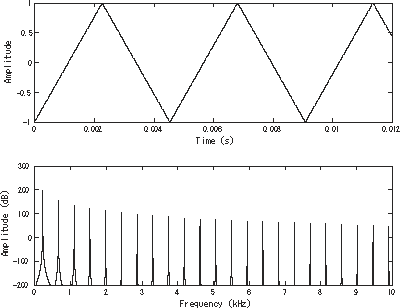
La onda triangular tiene un contenido en armónicos muy bajo,^[1] lo que concuerda con su parecido a una onda senoidal.^[2] Al igual que la onda cuadrada una onda triangular contiene solo armónicos impares, aunque con la diferencia que las amplitudes de los armónicos de la onda triangular decrecen más rápido (proporcional al inverso del cuadrado de su número armónico en lugar de solo el inverso).^[3][4]

Tanto matemática como físicamente se puede obtener integrando en el tiempo una onda cuadrada: los niveles constantes alto y bajo de dicha onda se convierten en las pendientes (constantes) de los flancos de subida y bajada de la onda triangular.

Expresión en funciones trigonométricas

Una onda triangular simétrica con período p y amplitud a puede expresarse en términos de seno y arcoseno (cuyos valores van de −π/2 a π/2): $${\displaystyle {\begin{aligned}y(x)={\frac {2a}{\pi }}\arcsin \left(\sin \left({\frac {2\pi }{p}}x\right)\right).\end{aligned}}}$$

Para una onda triangular con período 2 y amplitud 1:^[5] $${\displaystyle {\begin{aligned}y(x)={\frac {2}{\pi }}\arcsin \left(\sin \left(\pi x\right)\right).\end{aligned}}}$$

Armónicos

Onda triangular a 220 Hz, creada al sumar cada segundo armónicos impares sobre una onda senoidal.

Animación de la síntesis aditiva de una onda triangular simétrica mediante el incremento en el número de armónicos.

Es posible aproximar la señal onda triangular con síntesis aditiva sumando los armónicos impares de la fundamental mientras se multiplican cada otros armónicos singulares por -1 (o, equivalente, cambiando su fase por π) y multiplicando la amplitud de los armónicos por uno sobre el cuadrado de su número modal, n (la cual es equivalente a uno sobre el cuadrado de su frecuencia relativa a la fundamental).

Lo arriba expuesto puede ser descrito matemáticamente como lo siguiente:^[6]

${\displaystyle {\begin{aligned}x_{\mathrm {triangle} }(t)&{}={\frac {8}{\pi ^{2}}}\sum _{i=0}^{N-1}{\frac {(-1)^{i}}{n^{2}}}\sin(2\pi f_{0}nt),\end{aligned}}}$

Donde N es el número de armónicos que se incluyen en la aproximación, t es la variable independiente (p. ej. el tiempo para las ondas sonoras), ${\displaystyle f_{0}}$ es la frecuencia fundamental e i es la etiqueta armónica que está relacionada con el número modal por ${\displaystyle n=2i+1}$.

Esta infinita Serie de Fourier converge en la señal onda triangular como N que tiende a infinito.

Aplicaciones

Las ondas triangulares tienen aplicaciones destacadas, tales como:

• Generación de señales sinusoidales. Se generan ondas sinusoidales conformando la señal triangular con redes de resistencias y diodos. Es el método habitual para producir sinusoides en los generadores de funciones de baja frecuencia (hasta unos 10 MHz).
• Generación de barridos. En los tubos de rayos catódicos, se aplican tensiones triangulares asimétricas (diente de sierra) a las placas deflectoras, en el caso de osciloscopios, o corrientes de la misma forma a las bobinas deflectoras, en el caso de monitores de televisión, pantallas de ordenador, etc.
• Osciladores. Como la relación entre el tiempo y la amplitud de una onda triangular es lineal, resulta conveniente para realizar osciladores controlados por tensión, comparando su nivel con la tensión de control.

Véase también

• Función triangular
• Onda senoidal
• Onda cuadrada
• Onda de sierra
• Onda rectangular
• Oscilador
• Onda
• Sonido
• Zigzag