Arcoseno

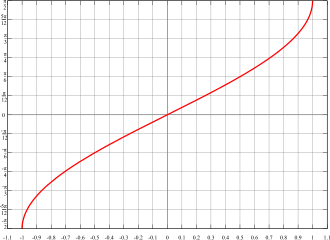
En trigonometría, el arcoseno está definido como la función inversa del seno de un ángulo. Desde un punto de vista geométrico, el arcoseno de un número ${\displaystyle x}$, denotado ${\displaystyle \arcsin x\,}$ corresponde al arco cuyo seno es ${\displaystyle x}$.

Función arcoseno
Gráfica de Función arcoseno
Definición	${\displaystyle \textstyle f{\mbox{ tal que }}f(\sin(x))=x\,}$
Tipo	Trigonométrica inversa
Dominio	${\displaystyle \textstyle [-1,1]}$
Codominio	${\displaystyle \textstyle [-{\frac {\pi }{2}},{\frac {\pi }{2}}]}$
Imagen	${\displaystyle \textstyle [-{\frac {\pi }{2}},{\frac {\pi }{2}}]}$
Propiedades	Estrictamente creciente Biyectiva en su dominio
Cálculo infinitesimal
Derivada	${\displaystyle {\frac {1}{\sqrt {1-x^{2}}}}}$
Función inversa	${\displaystyle \textstyle \sin(x)\quad x\in [-{\frac {\pi }{2}},{\frac {\pi }{2}}]}$
Funciones relacionadas	arcocoseno arcotangente
[editar datos en Wikidata]

La función seno no es biyectiva, por lo que no tiene función inversa definida en todo su dominio. Al restringir su dominio en ${\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}$ se obtiene una función inyectiva y por tanto con función inversa.

Propiedades

• Es una función inyectiva, estrictamente creciente.
• Como arcsen(-x) = -arcsenx, su gráfica es simétrica respecto al origen (0: 0)
• Su valor mínimo = -0.5π; su valor máximo = 0.5π.
• El origen de coordenadas es punto de inflexión con un ángulo de inclinación de 45°^[1]
• Es una función continua en todo su dominio.
• El cero de la función es 0. La gráfica corta al eje x en (0; 0)
• Es una función diferenciable, además analítica lo que permite un desarrollo en serie de potencias^[2]

Serie de potencias

El desarrollo en serie de potencias del arcoseno viene dado por:

${\displaystyle \sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}=x+{\frac {1}{6}}x^{3}+...}$

Nótese que este desarrollo solo es válido cuando se expresa el ángulo en radianes. A continuación se da una pequeña demostración de tal desarrollo.

Demostración

Aplicando el desarrollo en serie de Taylor es sencillo demostrar el siguiente desarrollo: ${\displaystyle {\frac {1}{\sqrt {1-t}}}=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}}}t^{n}}$ Efectuando el cambio t=s² se obtiene este desarrollo: ${\displaystyle {\frac {1}{\sqrt {1-s^{2}}}}=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}}}s^{2n}}$ Dado que: ${\displaystyle \arcsin(x)=\int _{0}^{x}{\frac {1}{\sqrt {1-s^{2}}}}ds}$ Integrando término a término la segunda serie se obtiene el desarrollo en serie del arcoseno: ${\displaystyle \arcsin(x)=\sum _{n=0}^{\infty }{\frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}}$

Extensión a la recta real y los números complejos

Como función analítica el arcoseno puede extenderse a valores fuera del dominio [-1,1] e incluso complejos. Para valores reales del argumento por encima de +1, la función toma valores complejos:

${\displaystyle \arcsin(1+\varepsilon ^{2})={\frac {\pi }{2}}-i\sum _{k=1}^{\infty }(-1)^{k+1}a_{k}\varepsilon ^{k},\quad a_{k}>0,\varepsilon \in \mathbb {R} }$

Para valores menores que -1, se tiene en cuenta que:

${\displaystyle \arcsin(-(1+\varepsilon ^{2}))=-\arcsin(1+\varepsilon ^{2})}$

Eso completa la extensión a los números reales, aunque fuera del intervalo [-1,+1] los valores de la función son complejos.

Aplicaciones

En un triángulo rectángulo, el arcoseno equivale a la expresión en radianes del ángulo agudo correspondiente a la razón entre su cateto opuesto y la hipotenusa.

Véase también

• Trigonometría
• Identidad trigonométrica

Referencias y notas

1. Bronshtein- Semendiaev: Manual de matemáticas Editorial Mir, Moscú, 2º edición
2. Conceptos que figuran en un libro de análisis matemático y aplicable a esta función

Enlaces externos

• Weisstein, Eric W. «Arcoseno». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.

• Datos: Q674517
• Multimedia: Arc sine function / Q674517