Funciones hiperbólicas inversas

En matemáticas, las funciones hiperbólicas inversas son las funciones inversas de las funciones hiperbólicas.

Un rayo desde el centro de la hipérbola unitaria ${\displaystyle \scriptstyle x^{2}\ -\ y^{2}\ =\ 1}$ hacia el punto ${\displaystyle \scriptstyle (\cosh \,a,\,\sinh \,a)}$, donde ${\displaystyle \scriptstyle a}$ es el doble del área entre el rayo, la hipérbola y el eje ${\displaystyle \scriptstyle x}$

Funciones hiperbólicas inversas

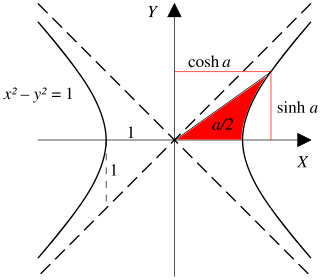
Para un valor dado de una función hiperbólica, la función hiperbólica inversa correspondiente proporciona el ángulo hiperbólico. El tamaño del ángulo hiperbólico es igual al área del sector hiperbólico correspondiente de la hipérbola xy = 1, o el doble del área del sector correspondiente de la hipérbola unitaria x² − y² = 1, al igual que un ángulo circular es el doble del área del sector circular de la circunferencia goniométrica. Algunos autores han llamado a las funciones hiperbólicas inversas "funciones de área", con el fin de dar un sentido más directo a los ángulos hiperbólicos.^{[1][2][3][4][5][6][7][8]}

Las funciones hiperbólicas aparecen en los cálculos de ángulos y distancias en geometría hiperbólica. También forman parte de las soluciones de muchas ecuaciones diferenciales lineales (como la ecuación que define una catenaria), ecuaciones de tercer grado y en la ecuación de Laplace en coordenadas cartesianas. La ecuación de Laplace es importante en muchas áreas de la física, incluido el electromagnetismo, la transferencia de calor, la fluidodinámica y la teoría de la relatividad especial.

Notación

Las abreviaturas más comunes son las especificadas por el estándar ISO/IEC 80000. Consisten en ar- seguido de la abreviatura de la función hiperbólica correspondiente (por ejemplo, arsinh, arcosh).

Sin embargo, arc- seguido de la función hiperbólica correspondiente (por ejemplo, arcsinh, arccosh) también se ve comúnmente, por analogía con la nomenclatura de las funciones trigonométricas inversas.^[9] Los primeros son nombres erróneos, ya que el prefijo arc es la abreviatura de arco, mientras que el prefijo ar significa área.^[10][11][12]

Otros autores prefieren usar la notación arg sinh, argcosh, argtanh, etc., donde el prefijo arg es la abreviatura del latín argumentum.^[13] En informática, a menudo se abrevia como "asinh".

También se usa la notación sinh⁻¹(x), cosh⁻¹(x), etc.,^{[14][15][16][17]} a pesar del hecho de que se debe tener cuidado para evitar malas interpretaciones del superíndice -1 como una potencia, en lugar de una abreviatura para denotar la función inversa (por ejemplo, cosh⁻¹(x) frente a cosh(x)⁻¹).

Definiciones en términos de logaritmos

Gráficas de las funciones trigonométricas e hiperbólicas (y sus funciones inversas)

Dado que las funciones hiperbólicas son funciones racionales de e^x cuyo numerador y denominador son de grado como máximo dos, estas funciones pueden resolverse en términos de e^x, utilizando la fórmula cuadrática; luego, tomando logaritmos naturales se obtienen las siguientes expresiones para las funciones hiperbólicas inversas.

Para los argumentos complejos, las funciones hiperbólicas inversas, raíz cuadrada y el logaritmo son funciones multivaluadas, y las igualdades de las siguientes subsecciones pueden verse como igualdades de funciones de varios valores.

Para todas las funciones hiperbólicas inversas (excepto la cotangente hiperbólica inversa y la cosecante hiperbólica inversa), el dominio de la función real es conexo.

Seno hiperbólico inverso

El seno hiperbólico inverso (también conocido como área del seno hiperbólico) (Latín: Area sinus hyperbolicus):^[14][15]

${\displaystyle \operatorname {arsinh} x=\log \left(x+{\sqrt {x^{2}+1}}\right)}$

El dominio es la recta real completa.

Coseno hiperbólico inverso

El coseno hiperbólico inverso (también conocido como área del coseno hiperbólico) (latín: Area cosinus hyperbolicus):^[14][15]

${\displaystyle \operatorname {arcosh} x=\log \left(x+{\sqrt {x^{2}-1}}\right)}$

El dominio es el intervalo [1, +∞ ).

Tangente hiperbólica inversa

La tangente hiperbólica inversa (también conocida como área de la tangente hiperbólica) (en latín: Area tangens hyperbolicus):^[15]

${\displaystyle \operatorname {artanh} x={\frac {1}{2}}\log \left({\frac {1+x}{1-x}}\right)}$

El dominio es el intervalo (−1, 1).

Cotangente hiperbólica inversa

La cotangente hiperbólica inversa (también conocida como área de la cotangente hiperbólica) (en latín: Area cotangens hyperbolicus):

${\displaystyle \operatorname {arcoth} x={\frac {1}{2}}\log \left({\frac {x+1}{x-1}}\right)}$

El dominio es la unión de los intervalos abiertos (−∞, −1) y (1, +∞).

Secante hiperbólica inversa

La secante hiperbólica inversa (también conocida como área de la secante hiperbólica) (en latín: Area secans hyperbolicus):

${\displaystyle \operatorname {arsech} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}-1}}\right)=\ln \left({\frac {1+{\sqrt {1-x^{2}}}}{x}}\right)}$

El dominio es el intervalo semiabierto (0, 1].

Cosecante hiperbólica inversa

La cosecante hiperbólica inversa (también conocida como área de la cosecante hiperbólica) (latín: Area cosecans hiperbolicus):

${\displaystyle \operatorname {arcsch} x=\ln \left({\frac {1}{x}}+{\sqrt {{\frac {1}{x^{2}}}+1}}\right)=\ln \left({\frac {1+{\sqrt {1+x^{2}}}}{x}}\right)}$

El dominio es toda la recta real, excepto el 0; y la última igualdad se tiene sólo si x>0.

Fórmulas de la suma

${\displaystyle \operatorname {arsinh} u\pm \operatorname {arsinh} v=\operatorname {arsinh} \left(u{\sqrt {1+v^{2}}}\pm v{\sqrt {1+u^{2}}}\right)}$

${\displaystyle \operatorname {arcosh} u\pm \operatorname {arcosh} v=\operatorname {arcosh} \left(uv\pm {\sqrt {(u^{2}-1)(v^{2}-1)}}\right)}$

${\displaystyle \operatorname {artanh} u\pm \operatorname {artanh} v=\operatorname {artanh} \left({\frac {u\pm v}{1\pm uv}}\right)}$

${\displaystyle {\begin{aligned}\operatorname {arsinh} u+\operatorname {arcosh} v&=\operatorname {arsinh} \left(uv+{\sqrt {(1+u^{2})(v^{2}-1)}}\right)\\&=\operatorname {arcosh} \left(v{\sqrt {1+u^{2}}}+u{\sqrt {v^{2}-1}}\right)\end{aligned}}}$

Otras identidades

${\displaystyle {\begin{aligned}2\operatorname {arcosh} x&=\operatorname {arcosh} (2x^{2}-1)&\quad {\hbox{ para }}x\geq 1\\4\operatorname {arcosh} x&=\operatorname {arcosh} (8x^{4}-8x^{2}+1)&\quad {\hbox{ para }}x\geq 1\\2\operatorname {arsinh} x&=\operatorname {arcosh} (2x^{2}+1)&\quad {\hbox{ para }}x\geq 0\\4\operatorname {arsinh} x&=\operatorname {arcosh} (8x^{4}+8x^{2}+1)&\quad {\hbox{ para }}x\geq 0\end{aligned}}}$

${\displaystyle \ln(x)=\operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)}$

Composición de funciones hiperbólicas e hiperbólicas inversas

${\displaystyle {\begin{aligned}&\sinh(\operatorname {arcosh} x)={\sqrt {x^{2}-1}}\quad {\text{para}}\quad |x|>1\\&\sinh(\operatorname {artanh} x)={\frac {x}{\sqrt {1-x^{2}}}}\quad {\text{para}}\quad -1<x<1\\&\cosh(\operatorname {arsinh} x)={\sqrt {1+x^{2}}}\\&\cosh(\operatorname {artanh} x)={\frac {1}{\sqrt {1-x^{2}}}}\quad {\text{para}}\quad -1<x<1\\&\tanh(\operatorname {arsinh} x)={\frac {x}{\sqrt {1+x^{2}}}}\\&\tanh(\operatorname {arcosh} x)={\frac {\sqrt {x^{2}-1}}{x}}\quad {\text{para}}\quad |x|>1\end{aligned}}}$

Composición de funciones hiperbólicas y trigonométricas inversas

${\displaystyle \operatorname {arsinh} \left(\tan \alpha \right)=\operatorname {artanh} \left(\sin \alpha \right)=\ln \left({\frac {1+\sin \alpha }{\cos \alpha }}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\cos \alpha }}\right)}$

${\displaystyle \ln \left(\left|\tan \alpha \right|\right)=-\operatorname {artanh} \left(\cos 2\alpha \right)}$^[18]

Conversiones

${\displaystyle \ln x=\operatorname {artanh} \left({\frac {x^{2}-1}{x^{2}+1}}\right)=\operatorname {arsinh} \left({\frac {x^{2}-1}{2x}}\right)=\pm \operatorname {arcosh} \left({\frac {x^{2}+1}{2x}}\right)}$

${\displaystyle \operatorname {artanh} x=\operatorname {arsinh} \left({\frac {x}{\sqrt {1-x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\frac {1}{\sqrt {1-x^{2}}}}\right)}$

${\displaystyle \operatorname {arsinh} x=\operatorname {artanh} \left({\frac {x}{\sqrt {1+x^{2}}}}\right)=\pm \operatorname {arcosh} \left({\sqrt {1+x^{2}}}\right)}$

${\displaystyle \operatorname {arcosh} x=\left|\operatorname {arsinh} \left({\sqrt {x^{2}-1}}\right)\right|=\left|\operatorname {artanh} \left({\frac {\sqrt {x^{2}-1}}{x}}\right)\right|}$

Derivadas

${\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arsinh} x&{}={\frac {1}{\sqrt {x^{2}+1}}},{\text{ para todo }}x{\text{ real}}\\{\frac {d}{dx}}\operatorname {arcosh} x&{}={\frac {1}{\sqrt {x^{2}-1}}},{\text{ para todo }}x>1{\text{ real}}\\{\frac {d}{dx}}\operatorname {artanh} x&{}={\frac {1}{1-x^{2}}},{\text{ para todo }}|x|<1{\text{ real}}\\{\frac {d}{dx}}\operatorname {arcoth} x&{}={\frac {1}{1-x^{2}}},{\text{ para todo }}|x|>1{\text{ real}}\\{\frac {d}{dx}}\operatorname {arsech} x&{}={\frac {-1}{x{\sqrt {1-x^{2}}}}},{\text{ para todo }}x\in (0,1){\text{ real}}\\{\frac {d}{dx}}\operatorname {arcsch} x&{}={\frac {-1}{|x|{\sqrt {1+x^{2}}}}},{\text{ para todo }}x{\text{ real, excepto }}0\\\end{aligned}}}$

Ejemplo de una derivada: sea θ = arsinh x, entonces (donde sinh² θ = (sinh θ) ²):

${\displaystyle {\frac {d\,\operatorname {arsinh} x}{dx}}={\frac {d\theta }{d\sinh \theta }}={\frac {1}{\cosh \theta }}={\frac {1}{\sqrt {1+\sinh ^{2}\theta }}}={\frac {1}{\sqrt {1+x^{2}}}}.}$

Desarrollos en serie

Se pueden obtener desarrollos en serie para las funciones anteriores:

${\displaystyle {\begin{aligned}\operatorname {arsinh} x&=x-\left({\frac {1}{2}}\right){\frac {x^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcosh} x&=\ln(2x)-\left(\left({\frac {1}{2}}\right){\frac {x^{-2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-6}}{6}}+\cdots \right)\\&=\ln(2x)-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-2n}}{2n}},\qquad \left|x\right|>1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {artanh} x&=x+{\frac {x^{3}}{3}}+{\frac {x^{5}}{5}}+{\frac {x^{7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{2n+1}}{2n+1}},\qquad \left|x\right|<1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcsch} x=\operatorname {arsinh} {\frac {1}{x}}&=x^{-1}-\left({\frac {1}{2}}\right){\frac {x^{-3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{-5}}{5}}-\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{-7}}{7}}\pm \cdots \\&=\sum _{n=0}^{\infty }\left({\frac {(-1)^{n}(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arsech} x=\operatorname {arcosh} {\frac {1}{x}}&=\ln {\frac {2}{x}}-\left(\left({\frac {1}{2}}\right){\frac {x^{2}}{2}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {x^{4}}{4}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {x^{6}}{6}}+\cdots \right)\\&=\ln {\frac {2}{x}}-\sum _{n=1}^{\infty }\left({\frac {(2n)!}{2^{2n}(n!)^{2}}}\right){\frac {x^{2n}}{2n}},\qquad 0<x\leq 1\end{aligned}}}$

${\displaystyle {\begin{aligned}\operatorname {arcoth} x=\operatorname {artanh} {\frac {1}{x}}&=x^{-1}+{\frac {x^{-3}}{3}}+{\frac {x^{-5}}{5}}+{\frac {x^{-7}}{7}}+\cdots \\&=\sum _{n=0}^{\infty }{\frac {x^{-(2n+1)}}{2n+1}},\qquad \left|x\right|>1\end{aligned}}}$

La expansión asintótica para el arsinh x viene dada por

${\displaystyle \operatorname {arsinh} x=\ln(2x)+\sum \limits _{n=1}^{\infty }{\left({-1}\right)^{n-1}{\frac {\left({2n-1}\right)!!}{2n\left({2n}\right)!!}}}{\frac {1}{x^{2n}}}}$

Valores principales en el plano complejo

En el análisis complejo, las funciones hiperbólicas inversas son funciones multivaluadas, que son analíticas, excepto en un número finito de puntos. Para tales funciones, es común definir un valor principal, que es una función analítica de un solo valor que coincide con una rama específica de la función multivalor, sobre un dominio que consiste en un plano complejo en el que un número finito de arcos (generalmente rectas o segmentos) se han eliminado. Estos arcos se denominan ramas cortadas. Para especificar la rama, es decir, definir qué valor de la función multivalor se considera en cada punto, generalmente se define en un punto particular y se deduce el valor en todas las partes del dominio de definición del valor principal por extensión analítica. Cuando sea posible, es mejor definir el valor principal directamente, sin hacer referencia a la continuación analítica.

Por ejemplo, para la raíz cuadrada, el valor principal se define como la raíz cuadrada que tiene un número complejo positivo. Esto define una función analítica de valor único, que se define en todas partes, excepto para los valores reales no positivos de las variables (donde las dos raíces cuadradas tienen una parte real cero). Este valor principal de la función raíz cuadrada se denota como ${\displaystyle {\sqrt {x}}}$ en lo que sigue. De manera similar, el valor principal del logaritmo, denotado ${\displaystyle \operatorname {Log} }$ a continuación, se define como el valor para el cual un número complejo tiene el valor absoluto más pequeño. Se define en todas partes excepto en los valores reales no positivos de la variable, para los cuales dos valores diferentes del logaritmo alcanzan el mínimo.

Para todas las funciones hiperbólicas inversas, el valor principal puede definirse en términos de los valores principales de la raíz cuadrada y la función logarítmica. Sin embargo, en algunos casos, las fórmulas de las definiciones en términos de logaritmos no dan un valor principal correcto, ya que dan un dominio de definición que es demasiado pequeño y, en un caso, no conexo.

Valor principal del seno hiperbólico inverso

El valor principal del seno hiperbólico inverso está dado por

${\displaystyle \operatorname {arsinh} z=\operatorname {Log} (z+{\sqrt {z^{2}+1}}\,)\,.}$

El argumento de la raíz cuadrada es un número real no positivo, si y solo si z pertenece a uno de los intervalos [i, +i∞) y (−i∞, −i] del eje imaginario. Si el argumento del logaritmo es real, entonces es positivo. Por tanto, esta fórmula define un valor principal para arsinh, con cortes de rama [i, +i∞) y (−i∞, −i]. Esto es óptimo, ya que los cortes de rama deben conectar los puntos singulares i y −i al infinito.

Valor principal del coseno hiperbólico inverso

La fórmula para el coseno hiperbólico inverso dada en el coseno hiperbólico inverso no es conveniente, ya que similar a los valores principales del logaritmo y la raíz cuadrada, el valor principal del arcosh no estaría definido para z imaginario. Por lo tanto, la raíz cuadrada debe factorizarse, lo que lleva a

${\displaystyle \operatorname {arcosh} z=\operatorname {Log} (z+{\sqrt {z+1}}{\sqrt {z-1}}\,)\,.}$

Los valores principales de las raíces cuadradas están definidos, excepto si z pertenece al intervalo real (−∞, 1]. Si el argumento del logaritmo es real, z es real y tiene el mismo signo. Por tanto, la fórmula anterior define un valor principal del arcosh fuera del intervalo real (−∞, 1], que es, por tanto, el único corte de rama.

Valores principales de la tangente y de la cotangente hiperbólicas inversas

Las fórmulas dadas en las definiciones en términos de logaritmos sugieren que

${\displaystyle {\begin{aligned}\operatorname {artanh} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {1+z}{1-z}}\right)\\\operatorname {arcoth} z&={\frac {1}{2}}\operatorname {Log} \left({\frac {z+1}{z-1}}\right)\end{aligned}}}$

para la definición de los valores principales de la tangente y de la cotangente hiperbólicas inversas. En estas fórmulas, el argumento del logaritmo es real si y solo si z es real. Para artanh, este argumento está en el intervalo real (−∞, 0], si z pertenece a (−∞, −1] o [1, ∞). Para el arcoth, el argumento del logaritmo está en (−∞, 0], si y solo si z pertenece al intervalo real [−1, 1].

Por lo tanto, estas fórmulas definen valores principales convenientes, para los cuales los cortes de rama son (−∞, −1] y [1, ∞) para la tangente hiperbólica inversa y [−1, 1] para la cotangente hiperbólica inversa.

En vista de una mejor evaluación numérica cerca de los cortes de rama, algunos autores utilizan las siguientes definiciones de los valores principales, aunque el segundo introduce una singularidad evitable en z = 0. Las dos definiciones de ${\displaystyle \operatorname {artanh} }$ difieren para los valores reales de ${\displaystyle z}$ con ${\displaystyle z>1}$. Los de ${\displaystyle \operatorname {arcoth} }$ difieren para los valores reales de ${\displaystyle z}$ con ${\displaystyle z\in [0,1)}$.

${\displaystyle {\begin{aligned}\operatorname {artanh} z&={\tfrac {1}{2}}\operatorname {Log} \left({1+z}\right)-{\tfrac {1}{2}}\operatorname {Log} \left({1-z}\right)\\\operatorname {arcoth} z&={\tfrac {1}{2}}\operatorname {Log} \left({1+{\frac {1}{z}}}\right)-{\tfrac {1}{2}}\operatorname {Log} \left({1-{\frac {1}{z}}}\right)\end{aligned}}}$

Valor principal de la cosecante hiperbólica inversa

Para la cosecante hiperbólica inversa, el valor principal se define como

${\displaystyle \operatorname {arcsch} z=\operatorname {Log} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z^{2}}}+1}}\,\right)}$.

Se define cuando los argumentos del logaritmo y la raíz cuadrada no son números reales no positivos. El valor principal de la raíz cuadrada se define así fuera del intervalo [−i, i] de la recta imaginaria. Si el argumento del logaritmo es real, entonces z es un número real distinto de cero, y esto implica que el argumento del logaritmo es positivo.

Así, el valor principal está definido por la fórmula anterior fuera del corte de rama, que consiste en el intervalo [−i, i] de la línea imaginaria.

Para z = 0, hay un punto singular que se incluye en el corte de rama.

Valor principal de la secante hiperbólica inversa

Aquí, como en el caso del coseno hiperbólico inverso, se tiene que factorizar la raíz cuadrada. Esto da el valor principal

${\displaystyle \operatorname {arsech} z=\operatorname {Log} \left({\frac {1}{z}}+{\sqrt {{\frac {1}{z}}+1}}\,{\sqrt {{\frac {1}{z}}-1}}\right).}$

Si el argumento de una raíz cuadrada es real, entonces z es real, y se deduce que ambos valores principales de raíces cuadradas están definidos, excepto si z es real y pertenece a uno de los intervalos (−∞, 0] y [1, +∞). Si el argumento del logaritmo es real y negativo, z también es real y negativo. De ello se deduce que el valor principal de arsech está bien definido, por la fórmula anterior fuera de dos cortes de rama, los intervalos reales (−∞, 0] y [1, +∞).

Para z = 0, hay un punto singular que se incluye en uno de los cortes de rama.

Representación gráfica

En la siguiente representación gráfica de los valores principales de las funciones hiperbólicas inversas, los cortes de las ramas aparecen como discontinuidades del color. El hecho de que todos los cortes de rama aparezcan como discontinuidades, muestra que estos valores principales pueden no extenderse a funciones analíticas definidas en dominios más amplios. En otras palabras, los cortes de rama definidos anteriormente son mínimos.

${\displaystyle \operatorname {arsinh} (z)}$

${\displaystyle \operatorname {arcosh} (z)}$

${\displaystyle \operatorname {artanh} (z)}$

${\displaystyle \operatorname {arcoth} (z)}$

${\displaystyle \operatorname {arsech} (z)}$

${\displaystyle \operatorname {arcsch} (z)}$

Funciones hiperbólicas inversas en el plano z complejo: el color en cada punto del plano representa el valor complejo de la función respectiva en ese punto

Véase también

• Logaritmo complejo
• Distribución secante hiperbólica
• ISO/IEC 80000
• Anexo:Integrales de funciones inversas hiperbólicas