Círculo

No debe confundirse con Circunferencia.

Para otros usos de este término, véase Círculo (desambiguación).

El círculo es una región del plano delimitada por una circunferencia y, por tanto, tiene asociada un área.^[1][2]Por tanto, es el área del plano en que se sitúan los puntos que distan del centro de la circunferencia una magnitud igual o inferior al radio.

Un círculo es el lugar geométrico de los puntos del plano cuya distancia a otro punto fijo, llamado centro, es menor o igual que una cantidad constante, llamada radio.

Un círculo.

En ocasiones «círculo» se confunde con «circunferencia», siendo esta última su borde, es decir, la curva perimetral que lo determina y que solo posee longitud.^[3]

Partes

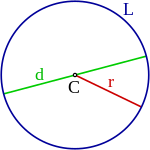
Elementos relevantes del círculo compartidos con la circunferencia por ser su borde:

• El centro es el centro de su circunferencia y, por tanto, equidistante a todos los puntos de esta. Señalado con el nombre ${\displaystyle C}$ en la figura.
• Un radio es cualquier segmento que une el centro con un punto de su circunferencia. El radio también es la longitud de los segmentos del mismo nombre. Señalado con el nombre ${\displaystyle r}$ en la figura. Su longitud es la mitad que la del diámetro.
• Un diámetro es cualquier segmento que une dos puntos de su circunferencia pasando por su centro. El diámetro también es la longitud de los segmento del mismo nombre. Señalado con el nombre ${\displaystyle d}$ en la figura. Su longitud es el doble que la del radio.
• El perímetro es el contorno del círculo y su longitud. Señalado con el nombre ${\displaystyle L}$ en la figura.

• Una cuerda es cualquier segmento que une dos puntos de su circunferencia. El diámetro es una cuerda de máxima longitud. Segmento verde en la figura es una cuerda. Si pasara por el centro sería la cuerda de mayor tamaño, es decir el diámetro.
• Un arco es cualquier porción de su circunferencia delimitada por dos puntos sobre esta. Se dice también que una cuerda subtiende cada arco que determinan sus extremos. Línea curva azul en la figura.
• Una flecha o sagita respecto una cuerda es el segmento de su mediatriz que hay entre esta cuerda y el arco que determina esta, sin pasar por el centro. Segmento rojo en la figura.

Perímetro

Artículo principal: Circunferencia

El perímetro de un círculo es el de su circunferencia y en función del radio ${\displaystyle r}$ o del diámetro ${\displaystyle d=2\cdot r}$ tiene el valor:

${\displaystyle \ell =2\cdot \pi \cdot r=}$ ${\displaystyle \pi \cdot d.}$

donde ${\displaystyle \pi =3,14159\dots }$ es la constante pi, de la circunferencia.

Área

El área de un círculo de radio ${\displaystyle r}$ o diámetro ${\displaystyle d=2\cdot r}$, tendrá un valor:

${\displaystyle A={\frac {\ell \cdot r}{2}}=}$ ${\displaystyle \pi \cdot r^{2}=}$ ${\displaystyle {\frac {\pi \cdot d^{2}}{4}}}$

Actualmente el cálculo de áreas es un ejercicio básico del tema de integrales. Históricamente fue aproximada mediante dos subdivisiones progresivas con sucesivos triángulos isósceles con dos lados radiales, la unión de la primera subdivisión era inscrita y la unión de la segunda subdivisión era circunscrita, quedando dos sumatorios cuyos límites coincidían y demostraban la unicidad del valor. Didácticamente hay demostraciones no rigurosas al deshacer la curvatura del círculo en figuras rectilíneas: Se puede mostrar una idea del despiece del círculo en sectores circulares tan estrechos como se desee para omitir la curvatura del borde del círculo. Wikiversidad alberga proyectos de aprendizaje sobre Círculo.

Propiedades

• Solo las rectas que contenga el centro del círculo puede ser un eje de simetría de este.
• Los círculos son invariantes a cualquier rotación con el eje en el centro de este círculo.

Posiciones relativas respecto el círculo

Véase también: Posiciones relativas en la circunferencia

Rectas

Posiciones de las rectas respecto del círculo:

• Una recta exterior es cualquier recta que no tiene puntos en común con el círculo. Señalada con el nombre ${\displaystyle a}$ en la figura.
• Una recta tangente es cualquier recta que toca al círculo en un único punto. Señalada con el nombre ${\displaystyle c}$ en la figura.
• Una recta secante es cualquier recta que divide al círculo en dos partes.^[4] Señalada con el nombre ${\displaystyle b}$ y los puntos de intersección ${\displaystyle A}$ y ${\displaystyle B}$ en la figura.

Se llama punto de tangencia cada uno de los puntos que comparte el círculo con los diferentes elementos tangentes, es decir, el punto donde se produce la tangencia. En todo punto de su circunferencia se pueden hacer tangencias.

Propiedades

• Toda recta tangente a un círculo es perpendicular al radio que contiene el punto de tangencia.

Entre círculos

Posiciones entre círculos:

• Un círculo es disjunto a otro, si no tiene puntos comunes con el otro. Véase la figura 1.
• Un círculo es tangente exterior a otro, si tienen un único punto común en sus bordes y, por tanto, todos los demás puntos del uno son exteriores al otro. Véase la figura 2.
• Un círculo es interior a otro si, todos sus puntos son comunes al otro, es decir, el conjunto de sus puntos están contenidos en el otro. Véase la figura 5.
• Un círculo es tangente interior a otro, si es interior y tiene un único punto común en sus bordes. Véase la figura 4.
• Son excéntricos los círculos que no tienen el mismo centro. Véase la figura 4.
• Son concéntricos los círculos que tienen el mismo centro, es decir, los que no son excéntricos. Véase la figura 5.
• Son coincidentes los círculos que tienen el mismo centro y el mismo radio, es decir, que todos los puntos de uno son los del otro y viceversa, y por tanto indistinguibles.

Propiedades

• Los centros de los círculos tangentes están alineados con el punto de tangencia.

Ángulos en un círculo

Artículo principal: Circunferencia#Ángulos en una circunferencia

Posición de los ángulos respecto de un círculo, puede ser:

• Un ángulo central es el que tiene su vértice en el centro del círculo.^[5]
• Un ángulo inscrito es el que tiene su vértice sobre el borde del círculo y cada lado determina una cuerda sobre este.^[5]
• Un ángulo semi-inscrito es el que tiene su vértice sobre el borde del círculo y uno de sus lados secantes determina una cuerda y el otro determina una recta tangente al círculo, es decir, que el vértice es un punto de tangencia.^[5]

Regiones circulares

Elementos relacionados con partes de las regiones del círculo, figura 1:

• El semicírculo es cualquier parte del círculo delimitada por un diámetro y el arco o semicircunferencia que determina este diámetro sobre su circunferencia. Véase la figura 2.
• El segmento circular es cualquier parte del círculo delimitada por una cuerda y uno de los arcos que determina esta cuerda sobre su circunferencia. Véase la figura 3.
• El segmento circular de dos bases, es cualquier parte del círculo delimitada entre dos cuerdas paralelas y los arcos que determinan estos sobre su circunferencia.^[6] Véase figura 4.
• El sector circular es cualquier parte del círculo delimitada por dos radios y el arco que determinan estos lados sobre su circunferencia, por tanto, queda unívocamente determinada por un ángulo central. Véase figura 5.
• La corona circular es la región del plano delimitada entre dos circunferencias concéntricas, exterior a la de radio menor e interior a la de radio mayor. Véase figura 6.
• El trapecio circular es cualquier parte de la corona circular delimitada por un ángulo central. Véase figura 7.
• La lúnula es cualquier región del plano delimitada por dos circunferencias secantes, interior a una y exterior a la otra. Véase figura 8.

Nota

En algunos textos y otros idiomas, para evitar referirse al interior de un ángulo o evitar aumentar las indicaciones, se hacen las distinciones siguientes:

• Se considera que un arco de circunferencia es menor cuando la medida de su longitud ${\displaystyle \ell }$ cumple que ${\displaystyle 0<\ell <\pi \cdot r}$ y se considera que un arco de circunferencia es mayor cuando la medida de su longitud ${\displaystyle \ell }$ cumple que ${\displaystyle \pi \cdot r<\ell <2\cdot \pi \cdot r.}$
• Se considera que un sector circular es menor cuando está determinado por el interior de un ángulo central ${\displaystyle \alpha }$ cuya medida cumple que ${\displaystyle 0<\alpha <180^{\circ },}$ véase la figura 2, y se considera que un sector circular es mayor cuando está determinado por el interior de un ángulo central ${\displaystyle \alpha }$ cuya medida cumple que ${\displaystyle 180^{\circ }<\alpha <360^{\circ },}$ véase la figura 3.
• Se considera que un segmento circular es menor cuando está delimitado un arco menor y una cuerda que lo subtiende, véase la figura 1, y se considera que un segmento circular es mayor cuando está delimitado por un arco mayor y una cuerda que lo subtiende, véase la figura 4.

Círculo en topología

Se cambia el uso de círculo por el de disco o más en general bola para analizar o fundamentar espacios topológicos con más precisión.

• Una bola cerrada centrada en ${\displaystyle P=(p_{1},\,p_{2})}$ y radio ${\displaystyle r}$ viene dada por ${\displaystyle B(P,\,r)=}$ ${\displaystyle \{(x,\,y)|\|P-(x,\,y)\|<r\}=}$ ${\displaystyle \{(x,\,y)|(p_{1}-x)^{2}+(p_{2}-y)^{2}<r\}}$. Esta sería la definición equivalente a círculo donde el centro es el punto ${\displaystyle P}$ y radio el valor ${\displaystyle r}$.

Llamativamente, geómetras y topólogos adoptan convenios diferentes para el significado de la hiperesfera o "n-esfera". Para los geómetras, la superficie de la esfera es llamada 3-esfera, mientras que topólogos se refieren a ella como 2-esfera.^[7]

Véase también

• Circunferencia
• Disco (topología)
• Cuadratura del círculo
• Grupo circular
• Esfera
• n-esfera
• 3-esfera
• Anexo:Ecuaciones de figuras geométricas

Referencias

1. Real Academia Española. «Círculo». Diccionario de la lengua española (23.ª edición).
2. Real Academia de Ciencias Exactas, Física y Naturales, ed. (1999). Diccionario esencial de las ciencias. Espsa. p. 190. ISBN 84-239-7921-0. «Región del plano limitada...»
3. Real Academia Española. «Circunferencia». Diccionario de la lengua española (23.ª edición).
4. De forma muy particular y para facilitar explicaciones didácticas en diferentes libros es posible encontrar como recta radial o recta diametral a las rectas que contienen al centro, un diámetro o un radio de una circunferencia.
5. RACEFN, ed. (1999). Diccionario Esencial de las Ciencias. Editorial Espasa Calpe, S.A. p. 61. ISBN 84-239-7921-0.
6. A veces conocido como faja circular o zona circular pero en general poco usada en bibliografía del tipo geometría o delineación evitando su nombre y describiéndolo sin asignar un nombre concreto.
7. «Sphere - from Wolfram MathWorld». Consultado el 2009.

Enlaces externos

• Wikcionario tiene definiciones y otra información sobre círculo.
• Wikimedia Commons alberga una categoría multimedia sobre círculos.
• Wikiversidad alberga proyectos de aprendizaje sobre Círculo.
• Círculo, en Descartes, del Centro Nacional de Información y Comunicación Educativa. Ministerio de Educación, Política Social y Deporte de España
• Círculo y circunferencia en webdelprofesor.ula.ve, de la Universidad de Los Andes, Venezuela
• Weisstein, Eric W. «Circunferencia». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. (acc. 17-03-09)
• Weisstein, Eric W. «Circumference». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. (longitud del perímetro del círculo) (acc. 17-03-09)
• Weisstein, Eric W. «Disk». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. (círculo: superficie plana limitada por una circunferencia) (acc. 17-03-09)

• Datos: Q17278
• Multimedia: Circle geometry / Q17278
• Citas célebres: Círculo