Test functions for optimization

In applied mathematics, test functions, known as artificial landscapes, are useful to evaluate characteristics of optimization algorithms, such as convergence rate, precision, robustness and general performance.

Here some test functions are presented with the aim of giving an idea about the different situations that optimization algorithms have to face when coping with these kinds of problems. In the first part, some objective functions for single-objective optimization cases are presented. In the second part, test functions with their respective Pareto fronts for multi-objective optimization problems (MOP) are given.

The artificial landscapes presented herein for single-objective optimization problems are taken from Bäck,^[1] Haupt et al.^[2] and from Rody Oldenhuis software.^[3] Given the number of problems (55 in total), just a few are presented here.

The test functions used to evaluate the algorithms for MOP were taken from Deb,^[4] Binh et al.^[5] and Binh.^[6] The software developed by Deb can be downloaded,^[7] which implements the NSGA-II procedure with GAs, or the program posted on Internet,^[8] which implements the NSGA-II procedure with ES.

Just a general form of the equation, a plot of the objective function, boundaries of the object variables and the coordinates of global minima are given herein.

Test functions for single-objective optimization

Name	Plot	Formula	Global minimum	Search domain
Rastrigin function		${\displaystyle f(\mathbf {x} )=An+\sum _{i=1}^{n}\left[x_{i}^{2}-A\cos(2\pi x_{i})\right]}$ ${\displaystyle {\text{where: }}A=10}$	${\displaystyle f(0,\dots ,0)=0}$	${\displaystyle -5.12\leq x_{i}\leq 5.12}$
Ackley function		${\displaystyle f(x,y)=-20\exp \left[-0.2{\sqrt {0.5\left(x^{2}+y^{2}\right)}}\right]}$ ${\displaystyle -\exp \left[0.5\left(\cos 2\pi x+\cos 2\pi y\right)\right]+e+20}$	${\displaystyle f(0,0)=0}$	${\displaystyle -5\leq x,y\leq 5}$
Sphere function		${\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{n}x_{i}^{2}}$	${\displaystyle f(x_{1},\dots ,x_{n})=f(0,\dots ,0)=0}$	${\displaystyle -\infty \leq x_{i}\leq \infty }$, ${\displaystyle 1\leq i\leq n}$
Rosenbrock function		${\displaystyle f({\boldsymbol {x}})=\sum _{i=1}^{n-1}\left[100\left(x_{i+1}-x_{i}^{2}\right)^{2}+\left(1-x_{i}\right)^{2}\right]}$	${\displaystyle {\text{Min}}={\begin{cases}n=2&\rightarrow \quad f(1,1)=0,\\n=3&\rightarrow \quad f(1,1,1)=0,\\n>3&\rightarrow \quad f(\underbrace {1,\dots ,1} _{n{\text{ times}}})=0\\\end{cases}}}$	${\displaystyle -\infty \leq x_{i}\leq \infty }$, ${\displaystyle 1\leq i\leq n}$
Beale function		${\displaystyle f(x,y)=\left(1.5-x+xy\right)^{2}+\left(2.25-x+xy^{2}\right)^{2}}$ ${\displaystyle +\left(2.625-x+xy^{3}\right)^{2}}$	${\displaystyle f(3,0.5)=0}$	${\displaystyle -4.5\leq x,y\leq 4.5}$
Goldstein–Price function		${\displaystyle f(x,y)=\left[1+\left(x+y+1\right)^{2}\left(19-14x+3x^{2}-14y+6xy+3y^{2}\right)\right]}$ ${\displaystyle \left[30+\left(2x-3y\right)^{2}\left(18-32x+12x^{2}+48y-36xy+27y^{2}\right)\right]}$	${\displaystyle f(0,-1)=3}$	${\displaystyle -2\leq x,y\leq 2}$
Booth function		${\displaystyle f(x,y)=\left(x+2y-7\right)^{2}+\left(2x+y-5\right)^{2}}$	${\displaystyle f(1,3)=0}$	${\displaystyle -10\leq x,y\leq 10}$
Bukin function N.6		${\displaystyle f(x,y)=100{\sqrt {\left|y-0.01x^{2}\right|}}+0.01\left|x+10\right|.\quad }$	${\displaystyle f(-10,1)=0}$	${\displaystyle -15\leq x\leq -5}$, ${\displaystyle -3\leq y\leq 3}$
Matyas function		${\displaystyle f(x,y)=0.26\left(x^{2}+y^{2}\right)-0.48xy}$	${\displaystyle f(0,0)=0}$	${\displaystyle -10\leq x,y\leq 10}$
Lévi function N.13		${\displaystyle f(x,y)=\sin ^{2}3\pi x+\left(x-1\right)^{2}\left(1+\sin ^{2}3\pi y\right)}$ ${\displaystyle +\left(y-1\right)^{2}\left(1+\sin ^{2}2\pi y\right)}$	${\displaystyle f(1,1)=0}$	${\displaystyle -10\leq x,y\leq 10}$
Griewank function		${\displaystyle f(x)=1+{\frac {1}{4000}}\sum _{i=1}^{n}x_{i}^{2}-\prod _{i=1}^{n}P_{i}(x_{i})}$, where ${\displaystyle P_{i}(x_{i})=\cos \left({\frac {x_{i}}{\sqrt {i}}}\right)}$	${\displaystyle f(0,\dots ,0)=0}$	${\displaystyle -\infty \leq x_{i}\leq \infty }$, ${\displaystyle 1\leq i\leq n}$
Himmelblau's function		${\displaystyle f(x,y)=(x^{2}+y-11)^{2}+(x+y^{2}-7)^{2}.\quad }$	${\displaystyle {\text{Min}}={\begin{cases}f\left(3.0,2.0\right)&=0.0\\f\left(-2.805118,3.131312\right)&=0.0\\f\left(-3.779310,-3.283186\right)&=0.0\\f\left(3.584428,-1.848126\right)&=0.0\\\end{cases}}}$	${\displaystyle -5\leq x,y\leq 5}$
Three-hump camel function		${\displaystyle f(x,y)=2x^{2}-1.05x^{4}+{\frac {x^{6}}{6}}+xy+y^{2}}$	${\displaystyle f(0,0)=0}$	${\displaystyle -5\leq x,y\leq 5}$
Easom function		${\displaystyle f(x,y)=-\cos \left(x\right)\cos \left(y\right)\exp \left(-\left(\left(x-\pi \right)^{2}+\left(y-\pi \right)^{2}\right)\right)}$	${\displaystyle f(\pi ,\pi )=-1}$	${\displaystyle -100\leq x,y\leq 100}$
Cross-in-tray function		${\displaystyle f(x,y)=-0.0001\left[\left|\sin x\sin y\exp \left(\left|100-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right|\right)\right|+1\right]^{0.1}}$	${\displaystyle {\text{Min}}={\begin{cases}f\left(1.34941,-1.34941\right)&=-2.06261\\f\left(1.34941,1.34941\right)&=-2.06261\\f\left(-1.34941,1.34941\right)&=-2.06261\\f\left(-1.34941,-1.34941\right)&=-2.06261\\\end{cases}}}$	${\displaystyle -10\leq x,y\leq 10}$
Eggholder function[9][10]		${\displaystyle f(x,y)=-\left(y+47\right)\sin {\sqrt {\left|{\frac {x}{2}}+\left(y+47\right)\right|}}-x\sin {\sqrt {\left|x-\left(y+47\right)\right|}}}$	${\displaystyle f(512,404.2319)=-959.6407}$	${\displaystyle -512\leq x,y\leq 512}$
Hölder table function		${\displaystyle f(x,y)=-\left|\sin x\cos y\exp \left(\left|1-{\frac {\sqrt {x^{2}+y^{2}}}{\pi }}\right|\right)\right|}$	${\displaystyle {\text{Min}}={\begin{cases}f\left(8.05502,9.66459\right)&=-19.2085\\f\left(-8.05502,9.66459\right)&=-19.2085\\f\left(8.05502,-9.66459\right)&=-19.2085\\f\left(-8.05502,-9.66459\right)&=-19.2085\end{cases}}}$	${\displaystyle -10\leq x,y\leq 10}$
McCormick function		${\displaystyle f(x,y)=\sin \left(x+y\right)+\left(x-y\right)^{2}-1.5x+2.5y+1}$	${\displaystyle f(-0.54719,-1.54719)=-1.9133}$	${\displaystyle -1.5\leq x\leq 4}$, ${\displaystyle -3\leq y\leq 4}$
Schaffer function N. 2		${\displaystyle f(x,y)=0.5+{\frac {\sin ^{2}\left(x^{2}-y^{2}\right)-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}}$	${\displaystyle f(0,0)=0}$	${\displaystyle -100\leq x,y\leq 100}$
Schaffer function N. 4		${\displaystyle f(x,y)=0.5+{\frac {\cos ^{2}\left[\sin \left(\left|x^{2}-y^{2}\right|\right)\right]-0.5}{\left[1+0.001\left(x^{2}+y^{2}\right)\right]^{2}}}}$	${\displaystyle {\text{Min}}={\begin{cases}f\left(0,1.25313\right)&=0.292579\\f\left(0,-1.25313\right)&=0.292579\\f\left(1.25313,0\right)&=0.292579\\f\left(-1.25313,0\right)&=0.292579\end{cases}}}$	${\displaystyle -100\leq x,y\leq 100}$
Styblinski–Tang function		${\displaystyle f({\boldsymbol {x}})={\frac {\sum _{i=1}^{n}x_{i}^{4}-16x_{i}^{2}+5x_{i}}{2}}}$	${\displaystyle -39.16617n<f(\underbrace {-2.903534,\ldots ,-2.903534} _{n{\text{ times}}})<-39.16616n}$	${\displaystyle -5\leq x_{i}\leq 5}$, ${\displaystyle 1\leq i\leq n}$..
Shekel function		${\displaystyle f({\vec {x}})=\sum _{i=1}^{m}\;\left(c_{i}+\sum \limits _{j=1}^{n}(x_{j}-a_{ji})^{2}\right)^{-1}}$ or, similarly, ${\displaystyle f(x_{1},x_{2},...,x_{n-1},x_{n})=\sum _{i=1}^{m}\;\left(c_{i}+\sum \limits _{j=1}^{n}(x_{j}-a_{ij})^{2}\right)^{-1}}$		${\displaystyle -\infty \leq x_{i}\leq \infty }$, ${\displaystyle 1\leq i\leq n}$

Test functions for constrained optimization

Name	Plot	Formula	Global minimum	Search domain
Rosenbrock function constrained to a disk[11]		${\displaystyle f(x,y)=(1-x)^{2}+100(y-x^{2})^{2}}$, subjected to: ${\displaystyle x^{2}+y^{2}\leq 2}$	${\displaystyle f(1.0,1.0)=0}$	${\displaystyle -1.5\leq x\leq 1.5}$, ${\displaystyle -1.5\leq y\leq 1.5}$
Mishra's Bird function - constrained[12][13]		${\displaystyle f(x,y)=\sin(y)e^{\left[(1-\cos x)^{2}\right]}+\cos(x)e^{\left[(1-\sin y)^{2}\right]}+(x-y)^{2}}$, subjected to: ${\displaystyle (x+5)^{2}+(y+5)^{2}<25}$	${\displaystyle f(-3.1302468,-1.5821422)=-106.7645367}$	${\displaystyle -10\leq x\leq 0}$, ${\displaystyle -6.5\leq y\leq 0}$
Townsend function (modified)[14]		${\displaystyle f(x,y)=-[\cos((x-0.1)y)]^{2}-x\sin(3x+y)}$, subjected to:${\displaystyle x^{2}+y^{2}<\left[2\cos t-{\frac {1}{2}}\cos 2t-{\frac {1}{4}}\cos 3t-{\frac {1}{8}}\cos 4t\right]^{2}+[2\sin t]^{2}}$ where: t = Atan2(x,y)	${\displaystyle f(2.0052938,1.1944509)=-2.0239884}$	${\displaystyle -2.25\leq x\leq 2.25}$, ${\displaystyle -2.5\leq y\leq 1.75}$
Keane's bump function[15]		${\displaystyle f(x)=-\left|{\frac {\left[\sum _{i=1}^{m}cos^{4}(x_{i})-2\prod _{i=1}^{m}cos^{2}(x_{i})\right]}{{\left(\sum _{i=1}^{m}ix_{i}^{2}\right)}^{0.5}}}\right|}$, subjected to: ${\displaystyle 0.75-\prod _{i=1}^{m}x_{i}<0}$, and ${\displaystyle \sum _{i=1}^{m}x_{i}-7.5m<0}$	${\displaystyle f((1.60025376,0.468675907))=-0.364979746}$	${\displaystyle 0<x_{i}<10}$

Test functions for multi-objective optimization

^{[further explanation needed]}

Name	Plot	Functions	Constraints	Search domain
Binh and Korn function:[5]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=4x^{2}+4y^{2}\\f_{2}\left(x,y\right)=\left(x-5\right)^{2}+\left(y-5\right)^{2}\\\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=\left(x-5\right)^{2}+y^{2}\leq 25\\g_{2}\left(x,y\right)=\left(x-8\right)^{2}+\left(y+3\right)^{2}\geq 7.7\\\end{cases}}}$	${\displaystyle 0\leq x\leq 5}$, ${\displaystyle 0\leq y\leq 3}$
Chankong and Haimes function:[16]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=2+\left(x-2\right)^{2}+\left(y-1\right)^{2}\\f_{2}\left(x,y\right)=9x-\left(y-1\right)^{2}\\\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=x^{2}+y^{2}\leq 225\\g_{2}\left(x,y\right)=x-3y+10\leq 0\\\end{cases}}}$	${\displaystyle -20\leq x,y\leq 20}$
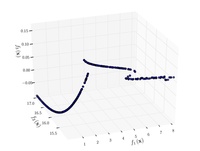
Fonseca–Fleming function:[17]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}-{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\f_{2}\left({\boldsymbol {x}}\right)=1-\exp \left[-\sum _{i=1}^{n}\left(x_{i}+{\frac {1}{\sqrt {n}}}\right)^{2}\right]\\\end{cases}}}$		${\displaystyle -4\leq x_{i}\leq 4}$, ${\displaystyle 1\leq i\leq n}$
Test function 4:[6]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=x^{2}-y\\f_{2}\left(x,y\right)=-0.5x-y-1\\\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=6.5-{\frac {x}{6}}-y\geq 0\\g_{2}\left(x,y\right)=7.5-0.5x-y\geq 0\\g_{3}\left(x,y\right)=30-5x-y\geq 0\\\end{cases}}}$	${\displaystyle -7\leq x,y\leq 4}$
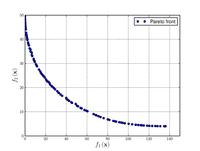
Kursawe function:[18]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{2}\left[-10\exp \left(-0.2{\sqrt {x_{i}^{2}+x_{i+1}^{2}}}\right)\right]\\&\\f_{2}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{3}\left[\left|x_{i}\right|^{0.8}+5\sin \left(x_{i}^{3}\right)\right]\\\end{cases}}}$		${\displaystyle -5\leq x_{i}\leq 5}$, ${\displaystyle 1\leq i\leq 3}$.
Schaffer function N. 1:[19]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x\right)=x^{2}\\f_{2}\left(x\right)=\left(x-2\right)^{2}\\\end{cases}}}$		${\displaystyle -A\leq x\leq A}$. Values of ${\displaystyle A}$ from ${\displaystyle 10}$ to ${\displaystyle 10^{5}}$ have been used successfully. Higher values of ${\displaystyle A}$ increase the difficulty of the problem.
Schaffer function N. 2:		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x\right)={\begin{cases}-x,&{\text{if }}x\leq 1\\x-2,&{\text{if }}1<x\leq 3\\4-x,&{\text{if }}3<x\leq 4\\x-4,&{\text{if }}x>4\\\end{cases}}\\f_{2}\left(x\right)=\left(x-5\right)^{2}\\\end{cases}}}$		${\displaystyle -5\leq x\leq 10}$.
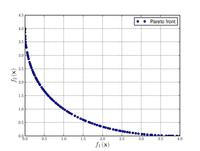
Poloni's two objective function:		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=\left[1+\left(A_{1}-B_{1}\left(x,y\right)\right)^{2}+\left(A_{2}-B_{2}\left(x,y\right)\right)^{2}\right]\\f_{2}\left(x,y\right)=\left(x+3\right)^{2}+\left(y+1\right)^{2}\\\end{cases}}}$ ${\displaystyle {\text{where}}={\begin{cases}A_{1}=0.5\sin \left(1\right)-2\cos \left(1\right)+\sin \left(2\right)-1.5\cos \left(2\right)\\A_{2}=1.5\sin \left(1\right)-\cos \left(1\right)+2\sin \left(2\right)-0.5\cos \left(2\right)\\B_{1}\left(x,y\right)=0.5\sin \left(x\right)-2\cos \left(x\right)+\sin \left(y\right)-1.5\cos \left(y\right)\\B_{2}\left(x,y\right)=1.5\sin \left(x\right)-\cos \left(x\right)+2\sin \left(y\right)-0.5\cos \left(y\right)\end{cases}}}$		${\displaystyle -\pi \leq x,y\leq \pi }$
Zitzler–Deb–Thiele's function N. 1:[20]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}\\\end{cases}}}$		${\displaystyle 0\leq x_{i}\leq 1}$, ${\displaystyle 1\leq i\leq 30}$.
Zitzler–Deb–Thiele's function N. 2:[20]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}}$		${\displaystyle 0\leq x_{i}\leq 1}$, ${\displaystyle 1\leq i\leq 30}$.
Zitzler–Deb–Thiele's function N. 3:[20]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+{\frac {9}{29}}\sum _{i=2}^{30}x_{i}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)\sin \left(10\pi f_{1}\left({\boldsymbol {x}}\right)\right)\end{cases}}}$		${\displaystyle 0\leq x_{i}\leq 1}$, ${\displaystyle 1\leq i\leq 30}$.
Zitzler–Deb–Thiele's function N. 4:[20]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=x_{1}\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=91+\sum _{i=2}^{10}\left(x_{i}^{2}-10\cos \left(4\pi x_{i}\right)\right)\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-{\sqrt {\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}}\end{cases}}}$		${\displaystyle 0\leq x_{1}\leq 1}$, ${\displaystyle -5\leq x_{i}\leq 5}$, ${\displaystyle 2\leq i\leq 10}$
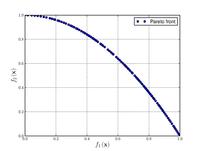
Zitzler–Deb–Thiele's function N. 6:[20]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=1-\exp \left(-4x_{1}\right)\sin ^{6}\left(6\pi x_{1}\right)\\f_{2}\left({\boldsymbol {x}}\right)=g\left({\boldsymbol {x}}\right)h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)\\g\left({\boldsymbol {x}}\right)=1+9\left[{\frac {\sum _{i=2}^{10}x_{i}}{9}}\right]^{0.25}\\h\left(f_{1}\left({\boldsymbol {x}}\right),g\left({\boldsymbol {x}}\right)\right)=1-\left({\frac {f_{1}\left({\boldsymbol {x}}\right)}{g\left({\boldsymbol {x}}\right)}}\right)^{2}\\\end{cases}}}$		${\displaystyle 0\leq x_{i}\leq 1}$, ${\displaystyle 1\leq i\leq 10}$.
Osyczka and Kundu function:[21]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left({\boldsymbol {x}}\right)=-25\left(x_{1}-2\right)^{2}-\left(x_{2}-2\right)^{2}-\left(x_{3}-1\right)^{2}-\left(x_{4}-4\right)^{2}-\left(x_{5}-1\right)^{2}\\f_{2}\left({\boldsymbol {x}}\right)=\sum _{i=1}^{6}x_{i}^{2}\\\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left({\boldsymbol {x}}\right)=x_{1}+x_{2}-2\geq 0\\g_{2}\left({\boldsymbol {x}}\right)=6-x_{1}-x_{2}\geq 0\\g_{3}\left({\boldsymbol {x}}\right)=2-x_{2}+x_{1}\geq 0\\g_{4}\left({\boldsymbol {x}}\right)=2-x_{1}+3x_{2}\geq 0\\g_{5}\left({\boldsymbol {x}}\right)=4-\left(x_{3}-3\right)^{2}-x_{4}\geq 0\\g_{6}\left({\boldsymbol {x}}\right)=\left(x_{5}-3\right)^{2}+x_{6}-4\geq 0\end{cases}}}$	${\displaystyle 0\leq x_{1},x_{2},x_{6}\leq 10}$, ${\displaystyle 1\leq x_{3},x_{5}\leq 5}$, ${\displaystyle 0\leq x_{4}\leq 6}$.
CTP1 function (2 variables):[4][22]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=x\\f_{2}\left(x,y\right)=\left(1+y\right)\exp \left(-{\frac {x}{1+y}}\right)\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)={\frac {f_{2}\left(x,y\right)}{0.858\exp \left(-0.541f_{1}\left(x,y\right)\right)}}\geq 1\\g_{2}\left(x,y\right)={\frac {f_{2}\left(x,y\right)}{0.728\exp \left(-0.295f_{1}\left(x,y\right)\right)}}\geq 1\end{cases}}}$	${\displaystyle 0\leq x,y\leq 1}$.
Constr-Ex problem:[4]		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=x\\f_{2}\left(x,y\right)={\frac {1+y}{x}}\\\end{cases}}}$	${\displaystyle {\text{s.t.}}={\begin{cases}g_{1}\left(x,y\right)=y+9x\geq 6\\g_{2}\left(x,y\right)=-y+9x\geq 1\\\end{cases}}}$	${\displaystyle 0.1\leq x\leq 1}$, ${\displaystyle 0\leq y\leq 5}$
Viennet function:		${\displaystyle {\text{Minimize}}={\begin{cases}f_{1}\left(x,y\right)=0.5\left(x^{2}+y^{2}\right)+\sin \left(x^{2}+y^{2}\right)\\f_{2}\left(x,y\right)={\frac {\left(3x-2y+4\right)^{2}}{8}}+{\frac {\left(x-y+1\right)^{2}}{27}}+15\\f_{3}\left(x,y\right)={\frac {1}{x^{2}+y^{2}+1}}-1.1\exp \left(-\left(x^{2}+y^{2}\right)\right)\\\end{cases}}}$		${\displaystyle -3\leq x,y\leq 3}$.