Runcinated 7-simplexes
From Wikipedia, the free encyclopedia
In seven-dimensional geometry, a runcinated 7-simplex is a convex uniform 7-polytope with 3rd order truncations (runcination) of the regular 7-simplex.
 7-simplex |
 Runcinated 7-simplex |
 Biruncinated 7-simplex |
 Runcitruncated 7-simplex |
 Biruncitruncated 7-simplex |
 Runcicantellated 7-simplex |
 Biruncicantellated 7-simplex |
 Runcicantitruncated 7-simplex |
 Biruncicantitruncated 7-simplex |
| Orthogonal projections in A7 Coxeter plane | ||
|---|---|---|
There are 8 unique runcinations of the 7-simplex with permutations of truncations, and cantellations.
Runcinated 7-simplex
| Runcinated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,3{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 2100 |
| Vertices | 280 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
- Small prismated octaexon (acronym: spo) (Jonathan Bowers)[1]
Coordinates
The vertices of the runcinated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,1,1,1,2). This construction is based on facets of the runcinated 8-orthoplex.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Biruncinated 7-simplex
| Biruncinated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t1,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 4200 |
| Vertices | 560 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
- Small biprismated octaexon (sibpo) (Jonathan Bowers)[2]
Coordinates
The vertices of the biruncinated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,1,1,2,2). This construction is based on facets of the biruncinated 8-orthoplex.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Runcitruncated 7-simplex
| runcitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,3{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 4620 |
| Vertices | 840 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
- Prismatotruncated octaexon (acronym: patto) (Jonathan Bowers)[3]
Coordinates
The vertices of the runcitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,1,1,2,3). This construction is based on facets of the runcitruncated 8-orthoplex.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Biruncitruncated 7-simplex
| Biruncitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t1,2,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 8400 |
| Vertices | 1680 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
- Biprismatotruncated octaexon (acronym: bipto) (Jonathan Bowers)[4]
Coordinates
The vertices of the biruncitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,1,2,3,3). This construction is based on facets of the biruncitruncated 8-orthoplex.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Runcicantellated 7-simplex
| runcicantellated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,3{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 3360 |
| Vertices | 840 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
- Prismatorhombated octaexon (acronym: paro) (Jonathan Bowers)[5]
Coordinates
The vertices of the runcicantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,1,2,2,3). This construction is based on facets of the runcicantellated 8-orthoplex.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Biruncicantellated 7-simplex
| biruncicantellated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t1,3,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | |
| Vertices | |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
- Biprismatorhombated octaexon (acronym: bipro) (Jonathan Bowers)
Coordinates
The vertices of the biruncicantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,2,2,3,3). This construction is based on facets of the biruncicantellated 8-orthoplex.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 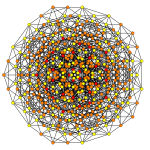 |
 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Runcicantitruncated 7-simplex
| runcicantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,3{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 5880 |
| Vertices | 1680 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
- Great prismated octaexon (acronym: gapo) (Jonathan Bowers)[6]
Coordinates
The vertices of the runcicantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,1,2,3,4). This construction is based on facets of the runcicantitruncated 8-orthoplex.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph |  |
 |
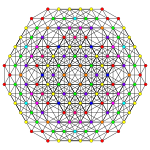 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
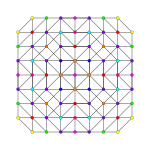 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Biruncicantitruncated 7-simplex
| biruncicantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t1,2,3,4{3,3,3,3,3,3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 11760 |
| Vertices | 3360 |
| Vertex figure | |
| Coxeter group | A7, [36], order 40320 |
| Properties | convex |
Alternate names
- Great biprismated octaexon (acronym: gibpo) (Jonathan Bowers)[7]
Coordinates
The vertices of the biruncicantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,2,3,4,4). This construction is based on facets of the biruncicantitruncated 8-orthoplex.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph |  |
 |
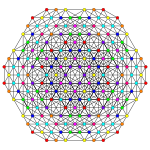 |
| Dihedral symmetry | [8] | [7] | [6] |
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph |  |
 |
 |
| Dihedral symmetry | [5] | [4] | [3] |
Related polytopes
These polytopes are among 71 uniform 7-polytopes with A7 symmetry.
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.