Top Qs
Timeline
Chat
Perspective
Cantellated 7-simplexes
From Wikipedia, the free encyclopedia
Remove ads
In seven-dimensional geometry, a cantellated 7-simplex is a convex uniform 7-polytope, being a cantellation of the regular 7-simplex.
There are unique 6 degrees of cantellation for the 7-simplex, including truncations.
Remove ads
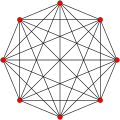
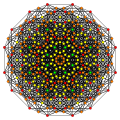
Cantellated 7-simplex
Summarize
Perspective
| Cantellated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | rr{3,3,3,3,3,3} or |
| Coxeter-Dynkin diagram | or |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 1008 |
| Vertices | 168 |
| Vertex figure | 5-simplex prism |
| Coxeter groups | A7, [3,3,3,3,3,3] |
| Properties | convex |
Alternate names
- Small rhombated octaexon (acronym: saro) (Jonathan Bowers)[1]
Coordinates
The vertices of the cantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,0,1,1,2). This construction is based on facets of the cantellated 8-orthoplex.
Images
Remove ads
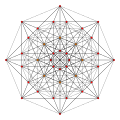
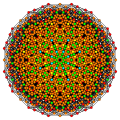
Bicantellated 7-simplex
Summarize
Perspective
Alternate names
- Small birhombated octaexon (acronym: sabro) (Jonathan Bowers)[2]
Coordinates
The vertices of the bicantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,1,1,2,2). This construction is based on facets of the bicantellated 8-orthoplex.
Images
Remove ads
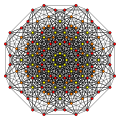
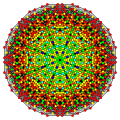
Tricantellated 7-simplex
Summarize
Perspective
Alternate names
- Small trirhombihexadecaexon (stiroh) (Jonathan Bowers)[3]
Coordinates
The vertices of the tricantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,1,2,2,2). This construction is based on facets of the tricantellated 8-orthoplex.
Images
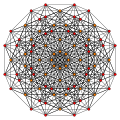
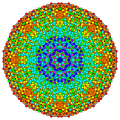
Cantitruncated 7-simplex
Summarize
Perspective
Alternate names
- Great rhombated octaexon (acronym: garo) (Jonathan Bowers)[4]
Coordinates
The vertices of the cantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,0,1,2,3). This construction is based on facets of the cantitruncated 8-orthoplex.
Images
Remove ads
Bicantitruncated 7-simplex
Summarize
Perspective
Alternate names
- Great birhombated octaexon (acronym: gabro) (Jonathan Bowers)[5]
Coordinates
The vertices of the bicantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,0,1,2,3,3). This construction is based on facets of the bicantitruncated 8-orthoplex.
Images
Remove ads
Tricantitruncated 7-simplex
Summarize
Perspective
Alternate names
- Great trirhombihexadecaexon (acronym: gatroh) (Jonathan Bowers)[6]
Coordinates
The vertices of the tricantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,0,0,1,2,3,4,4). This construction is based on facets of the tricantitruncated 8-orthoplex.
Images
Remove ads
Related polytopes
This polytope is one of 71 uniform 7-polytopes with A7 symmetry.
Remove ads
See also
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads















 ...
...




 ...
...




 ...
...




 ...
...




 ...
...