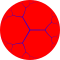
Order-3 apeirogonal tiling

In geometry, the order-3 apeirogonal tiling is a regular tiling of the hyperbolic plane. It is represented by the Schläfli symbol {∞,3}, having three regular apeirogons around each vertex. Each apeirogon is inscribed in a horocycle.

Order-3 apeirogonal tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic regular tiling
Vertex configuration	∞3
Schläfli symbol	{∞,3} t{∞,∞} t(∞,∞,∞)
Wythoff symbol	3 | ∞ 2 2 ∞ | ∞ ∞ ∞ ∞ |
Coxeter diagram
Symmetry group	[∞,3], (*∞32) [∞,∞], (*∞∞2) [(∞,∞,∞)], (*∞∞∞)
Dual	Infinite-order triangular tiling
Properties	Vertex-transitive, edge-transitive, face-transitive

The order-2 apeirogonal tiling represents an infinite dihedron in the Euclidean plane as {∞,2}.

Images

Each apeirogon face is circumscribed by a horocycle, which looks like a circle in a Poincaré disk model, internally tangent to the projective circle boundary.

Uniform colorings

Like the Euclidean hexagonal tiling, there are 3 uniform colorings of the order-3 apeirogonal tiling, each from different reflective triangle group domains:

Regular	Truncations
{∞,3}	t0,1{∞,∞}	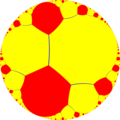t1,2{∞,∞}	t{∞[3]}
Hyperbolic triangle groups
[∞,3]	[∞,∞]		[(∞,∞,∞)]

Symmetry

The dual to this tiling represents the fundamental domains of [(∞,∞,∞)] (*∞∞∞) symmetry. There are 15 small index subgroups (7 unique) constructed from [(∞,∞,∞)] by mirror removal and alternation. Mirrors can be removed if its branch orders are all even, and cuts neighboring branch orders in half. Removing two mirrors leaves a half-order gyration point where the removed mirrors met. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The symmetry can be doubled as ∞∞2 symmetry by adding a mirror bisecting the fundamental domain. Dividing a fundamental domain by 3 mirrors creates a ∞32 symmetry.

A larger subgroup is constructed [(∞,∞,∞^*)], index 8, as (∞*∞^∞) with gyration points removed, becomes (*∞^∞).

Subgroups of [(∞,∞,∞)] (*∞∞∞)
Index	1	2			4
Diagram
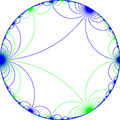Coxeter	[(∞,∞,∞)]	[(1+,∞,∞,∞)] =	[(∞,1+,∞,∞)] =	[(∞,∞,1+,∞)] =	[(1+,∞,1+,∞,∞)]	[(∞+,∞+,∞)]
Orbifold	*∞∞∞	*∞∞∞∞			∞*∞∞∞	∞∞∞×
Diagram
Coxeter		[(∞,∞+,∞)]	[(∞,∞,∞+)]	[(∞+,∞,∞)]	[(∞,1+,∞,1+,∞)]	[(1+,∞,∞,1+,∞)] =
Orbifold		∞*∞			∞*∞∞∞
Direct subgroups
Index	2	4			8
Diagram
Coxeter	[(∞,∞,∞)]+	[(∞,∞+,∞)]+ =	[(∞,∞,∞+)]+ =	[(∞+,∞,∞)]+ =	[(∞,1+,∞,1+,∞)]+ =
Orbifold	∞∞∞	∞∞∞∞			∞∞∞∞∞∞
Radical subgroups
Index	∞			∞
Diagram
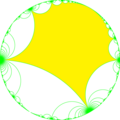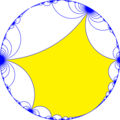Coxeter	[(∞,∞*,∞)]	[(∞,∞,∞*)]	[(∞*,∞,∞)]	[(∞,∞*,∞)]+	[(∞,∞,∞*)]+	[(∞*,∞,∞)]+
Orbifold	∞*∞∞			∞∞

Related polyhedra and tilings

This tiling is topologically related as a part of sequence of regular polyhedra with Schläfli symbol {n,3}.

*n32 symmetry mutation of regular tilings: {n,3} v t e
Spherical				Euclidean	Compact hyperb.		Paraco.	Noncompact hyperbolic
{2,3}	{3,3}	{4,3}	{5,3}	{6,3}	{7,3}	{8,3}	{∞,3}	{12i,3}	{9i,3}	{6i,3}	{3i,3}

Paracompact uniform tilings in [∞,3] family v t e
Symmetry: [∞,3], (*∞32)							[∞,3]+ (∞32)	[1+,∞,3] (*∞33)		[∞,3+] (3*∞)
		=	=	=				= or	= or	=
{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h2{∞,3}	s{3,∞}
Uniform duals
V∞3	V3.∞.∞	V(3.∞)2	V6.6.∞	V3∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)3		V3.3.3.3.3.∞

Paracompact uniform tilings in [∞,∞] family v t e
= =	= =	= =	= =	= =	=	=
{∞,∞}	t{∞,∞}	r{∞,∞}	2t{∞,∞}=t{∞,∞}	2r{∞,∞}={∞,∞}	rr{∞,∞}	tr{∞,∞}
Dual tilings
V∞∞	V∞.∞.∞	V(∞.∞)2	V∞.∞.∞	V∞∞	V4.∞.4.∞	V4.4.∞
Alternations
[1+,∞,∞] (*∞∞2)	[∞+,∞] (∞*∞)	[∞,1+,∞] (*∞∞∞∞)	[∞,∞+] (∞*∞)	[∞,∞,1+] (*∞∞2)	[(∞,∞,2+)] (2*∞∞)	[∞,∞]+ (2∞∞)
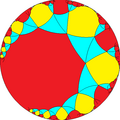h{∞,∞}	s{∞,∞}	hr{∞,∞}	s{∞,∞}	h2{∞,∞}	hrr{∞,∞}	sr{∞,∞}
Alternation duals
V(∞.∞)∞	V(3.∞)3	V(∞.4)4	V(3.∞)3	V∞∞	V(4.∞.4)2	V3.3.∞.3.∞

Paracompact uniform tilings in [(∞,∞,∞)] family v t e
(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) h2{∞,∞}	(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) h2{∞,∞}	(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) r{∞,∞}	t(∞,∞,∞) t{∞,∞}
Dual tilings
V∞∞	V∞.∞.∞.∞	V∞∞	V∞.∞.∞.∞	V∞∞	V∞.∞.∞.∞	V∞.∞.∞
Alternations
[(1+,∞,∞,∞)] (*∞∞∞∞)	[∞+,∞,∞)] (∞*∞)	[∞,1+,∞,∞)] (*∞∞∞∞)	[∞,∞+,∞)] (∞*∞)	[(∞,∞,∞,1+)] (*∞∞∞∞)	[(∞,∞,∞+)] (∞*∞)	[∞,∞,∞)]+ (∞∞∞)
Alternation duals
V(∞.∞)∞	V(∞.4)4	V(∞.∞)∞	V(∞.4)4	V(∞.∞)∞	V(∞.4)4	V3.∞.3.∞.3.∞

See also

• Tilings of regular polygons
• List of uniform planar tilings
• List of regular polytopes
• Hexagonal tiling honeycomb, similar {6,3,3} honeycomb in H³.

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

External links

• Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
• Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.