In geometry, the truncated order-4 apeirogonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{∞,4}.
| Truncated order-4 apeirogonal tiling | |
|---|---|
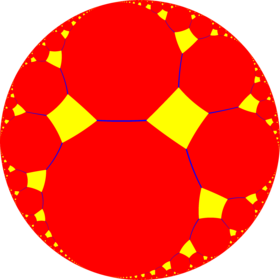 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 4.∞.∞ |
| Schläfli symbol | t{∞,4} tr{∞,∞} or |
| Wythoff symbol | 2 4 | ∞ 2 ∞ ∞ | |
| Coxeter diagram | |
| Symmetry group | [∞,4], (*∞42) [∞,∞], (*∞∞2) |
| Dual | Infinite-order tetrakis square tiling |
| Properties | Vertex-transitive |
Uniform colorings
A half symmetry coloring is tr{∞,∞}, has two types of apeirogons, shown red and yellow here. If the apeirogonal curvature is too large, it doesn't converge to a single ideal point, like the right image, red apeirogons below. Coxeter diagram are shown with dotted lines for these divergent, ultraparallel mirrors.
 (Vertex centered) |
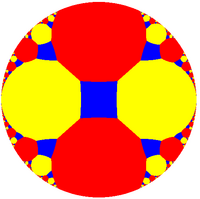 (Square centered) |
Symmetry
From [∞,∞] symmetry, there are 15 small index subgroup by mirror removal and alternation. Mirrors can be removed if its branch orders are all even, and cuts neighboring branch orders in half. Removing two mirrors leaves a half-order gyration point where the removed mirrors met. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The symmetry can be doubled as ∞42 symmetry by adding a mirror bisecting the fundamental domain. The subgroup index-8 group, [1+,∞,1+,∞,1+] (∞∞∞∞) is the commutator subgroup of [∞,∞].
| Index | 1 | 2 | 4 | |||
|---|---|---|---|---|---|---|
| Diagram | 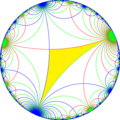 |
 |
 |
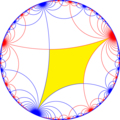 |
 |
 |
| Coxeter | [∞,∞] |
[1+,∞,∞] |
[∞,∞,1+] |
[∞,1+,∞] |
[1+,∞,∞,1+] |
[∞+,∞+] |
| Orbifold | *∞∞2 | *∞∞∞ | *∞2∞2 | *∞∞∞∞ | ∞∞× | |
| Semidirect subgroups | ||||||
| Diagram |  |
 |
 |
 |
 | |
| Coxeter | [∞,∞+] |
[∞+,∞] |
[(∞,∞,2+)] |
[∞,1+,∞,1+] = |
[1+,∞,1+,∞] = | |
| Orbifold | ∞*∞ | 2*∞∞ | ∞*∞∞ | |||
| Direct subgroups | ||||||
| Index | 2 | 4 | 8 | |||
| Diagram |  |
 |
 |
 |
 | |
| Coxeter | [∞,∞]+ |
[∞,∞+]+ |
[∞+,∞]+ |
[∞,1+,∞]+ |
[∞+,∞+]+ = [1+,∞,1+,∞,1+] | |
| Orbifold | ∞∞2 | ∞∞∞ | ∞2∞2 | ∞∞∞∞ | ||
| Radical subgroups | ||||||
| Index | ∞ | ∞ | ||||
| Diagram | 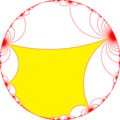 |
 |
 |
 | ||
| Coxeter | [∞,∞*] |
[∞*,∞] |
[∞,∞*]+ |
[∞*,∞]+ | ||
| Orbifold | *∞∞ | ∞∞ | ||||
Related polyhedra and tiling
| *n42 symmetry mutation of truncated tilings: 4.2n.2n | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry *n42 [n,4] |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | |||||||
| *242 [2,4] |
*342 [3,4] |
*442 [4,4] |
*542 [5,4] |
*642 [6,4] |
*742 [7,4] |
*842 [8,4]... |
*∞42 [∞,4] | ||||
| Truncated figures |
 |
 |
 |
 |
 |
 |
 |
 | |||
| Config. | 4.4.4 | 4.6.6 | 4.8.8 | 4.10.10 | 4.12.12 | 4.14.14 | 4.16.16 | 4.∞.∞ | |||
| n-kis figures |
 |
 |
 |
 |
 |
 |
 |
 | |||
| Config. | V4.4.4 | V4.6.6 | V4.8.8 | V4.10.10 | V4.12.12 | V4.14.14 | V4.16.16 | V4.∞.∞ | |||
| Paracompact uniform tilings in [∞,4] family | |||||||
|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 | |
| {∞,4} | t{∞,4} | r{∞,4} | 2t{∞,4}=t{4,∞} | 2r{∞,4}={4,∞} | rr{∞,4} | tr{∞,4} | |
| Dual figures | |||||||
 |
 |
 |
 |
 |
 |
 | |
| V∞4 | V4.∞.∞ | V(4.∞)2 | V8.8.∞ | V4∞ | V43.∞ | V4.8.∞ | |
| Alternations | |||||||
| [1+,∞,4] (*44∞) |
[∞+,4] (∞*2) |
[∞,1+,4] (*2∞2∞) |
[∞,4+] (4*∞) |
[∞,4,1+] (*∞∞2) |
[(∞,4,2+)] (2*2∞) |
[∞,4]+ (∞42) | |
= |
= |
||||||
| h{∞,4} | s{∞,4} | hr{∞,4} | s{4,∞} | h{4,∞} | hrr{∞,4} | s{∞,4} | |
 |
 |
 |
 | ||||
| Alternation duals | |||||||
 |
 |
||||||
| V(∞.4)4 | V3.(3.∞)2 | V(4.∞.4)2 | V3.∞.(3.4)2 | V∞∞ | V∞.44 | V3.3.4.3.∞ | |
| Paracompact uniform tilings in [∞,∞] family | ||||||
|---|---|---|---|---|---|---|
= = |
= = |
= = |
= = |
= = |
= |
= |
 |
 |
 |
 |
 |
 |
 |
| {∞,∞} | t{∞,∞} | r{∞,∞} | 2t{∞,∞}=t{∞,∞} | 2r{∞,∞}={∞,∞} | rr{∞,∞} | tr{∞,∞} |
| Dual tilings | ||||||
 |
 |
 |
 |
 |
 |
 |
| V∞∞ | V∞.∞.∞ | V(∞.∞)2 | V∞.∞.∞ | V∞∞ | V4.∞.4.∞ | V4.4.∞ |
| Alternations | ||||||
| [1+,∞,∞] (*∞∞2) |
[∞+,∞] (∞*∞) |
[∞,1+,∞] (*∞∞∞∞) |
[∞,∞+] (∞*∞) |
[∞,∞,1+] (*∞∞2) |
[(∞,∞,2+)] (2*∞∞) |
[∞,∞]+ (2∞∞) |
 |
 |
 |
 |
 |
 | |
| h{∞,∞} | s{∞,∞} | hr{∞,∞} | s{∞,∞} | h2{∞,∞} | hrr{∞,∞} | sr{∞,∞} |
| Alternation duals | ||||||
 |
 |
 |
 | |||
| V(∞.∞)∞ | V(3.∞)3 | V(∞.4)4 | V(3.∞)3 | V∞∞ | V(4.∞.4)2 | V3.3.∞.3.∞ |
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.

