Regular 4-polytope

In mathematics, a regular 4-polytope or regular polychoron is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.

The tesseract is one of 6 convex regular 4-polytopes

There are six convex and ten star regular 4-polytopes, giving a total of sixteen.

History

The convex regular 4-polytopes were first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.^[1] He discovered that there are precisely six such figures.

Schläfli also found four of the regular star 4-polytopes: the grand 120-cell, great stellated 120-cell, grand 600-cell, and great grand stellated 120-cell. He skipped the remaining six because he would not allow forms that failed the Euler characteristic on cells or vertex figures (for zero-hole tori: F − E + V = 2). That excludes cells and vertex figures such as the great dodecahedron {5,⁠5/2⁠} and small stellated dodecahedron {⁠5/2⁠,5}.

Edmund Hess (1843–1903) published the complete list in his 1883 German book Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder.

Construction

The existence of a regular 4-polytope ${\displaystyle \{p,q,r\}}$ is constrained by the existence of the regular polyhedra ${\displaystyle \{p,q\},\{q,r\}}$ which form its cells and a dihedral angle constraint

${\displaystyle \sin {\frac {\pi }{p}}\sin {\frac {\pi }{r}}>\cos {\frac {\pi }{q}}}$

to ensure that the cells meet to form a closed 3-surface.

The six convex and ten star polytopes described are the only solutions to these constraints.

There are four nonconvex Schläfli symbols {p,q,r} that have valid cells {p,q} and vertex figures {q,r}, and pass the dihedral test, but fail to produce finite figures: {3,⁠5/2⁠,3}, {4,3,⁠5/2⁠}, {⁠5/2⁠,3,4}, {⁠5/2⁠,3,⁠5/2⁠}.

Regular convex 4-polytopes

The regular convex 4-polytopes are the four-dimensional analogues of the Platonic solids in three dimensions and the convex regular polygons in two dimensions.

Each convex regular 4-polytope is bounded by a set of 3-dimensional cells which are all Platonic solids of the same type and size. These are fitted together along their respective faces (face-to-face) in a regular fashion, forming the surface of the 4-polytope which is a closed, curved 3-dimensional space (analogous to the way the surface of the earth is a closed, curved 2-dimensional space).

Properties

Like their 3-dimensional analogues, the convex regular 4-polytopes can be naturally ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. Each greater polytope in the sequence is rounder than its predecessor, enclosing more content within the same radius.^[2] The 4-simplex (5-cell) has the smallest content, and the 120-cell has the largest.

Regular convex 4-polytopes
Symmetry group	A4	B4		F4	H4
Name	5-cell Hyper-tetrahedron 5-point	16-cell Hyper-octahedron 8-point	8-cell Hyper-cube 16-point	24-cell 24-point	600-cell Hyper-icosahedron 120-point	120-cell Hyper-dodecahedron 600-point
Schläfli symbol	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Coxeter mirrors
Mirror dihedrals	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/4⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/5⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠	⁠𝝅/5⁠ ⁠𝝅/3⁠ ⁠𝝅/3⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠ ⁠𝝅/2⁠
Graph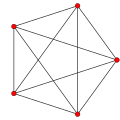
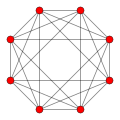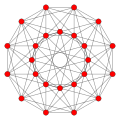Vertices	5 tetrahedral	8 octahedral	16 tetrahedral	24 cubical	120 icosahedral	600 tetrahedral
Edges	10 triangular	24 square	32 triangular	96 triangular	720 pentagonal	1200 triangular
Faces	10 triangles	32 triangles	24 squares	96 triangles	1200 triangles	720 pentagons
Cells	5 tetrahedra	16 tetrahedra	8 cubes	24 octahedra	600 tetrahedra	120 dodecahedra
Tori	1 5-tetrahedron	2 8-tetrahedron	2 4-cube	4 6-octahedron	20 30-tetrahedron	12 10-dodecahedron
Inscribed	120 in 120-cell	675 in 120-cell	2 16-cells	3 8-cells	25 24-cells	10 600-cells
Great polygons		2 squares x 3	4 rectangles x 4	4 hexagons x 4	12 decagons x 6	100 irregular hexagons x 4
Petrie polygons	1 pentagon x 2	1 octagon x 3	2 octagons x 4	2 dodecagons x 4	4 30-gons x 6	20 30-gons x 4
Long radius	${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle 1}$
Edge length	${\displaystyle {\sqrt {\tfrac {5}{2}}}\approx 1.581}$	${\displaystyle {\sqrt {2}}\approx 1.414}$	${\displaystyle 1}$	${\displaystyle 1}$	${\displaystyle {\tfrac {1}{\phi }}\approx 0.618}$	${\displaystyle {\tfrac {1}{\phi ^{2}{\sqrt {2}}}}\approx 0.270}$
Short radius	${\displaystyle {\tfrac {1}{4}}}$	${\displaystyle {\tfrac {1}{2}}}$	${\displaystyle {\tfrac {1}{2}}}$	${\displaystyle {\sqrt {\tfrac {1}{2}}}\approx 0.707}$	${\displaystyle {\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926}$	${\displaystyle {\sqrt {\tfrac {\phi ^{4}}{8}}}\approx 0.926}$
Area	${\displaystyle 10\left({\tfrac {5{\sqrt {3}}}{8}}\right)\approx 10.825}$	${\displaystyle 32\left({\sqrt {\tfrac {3}{4}}}\right)\approx 27.713}$	${\displaystyle 24}$	${\displaystyle 96\left({\sqrt {\tfrac {3}{16}}}\right)\approx 41.569}$	${\displaystyle 1200\left({\tfrac {\sqrt {3}}{4\phi ^{2}}}\right)\approx 198.48}$	${\displaystyle 720\left({\tfrac {\sqrt {25+10{\sqrt {5}}}}{8\phi ^{4}}}\right)\approx 90.366}$
Volume	${\displaystyle 5\left({\tfrac {5{\sqrt {5}}}{24}}\right)\approx 2.329}$	${\displaystyle 16\left({\tfrac {1}{3}}\right)\approx 5.333}$	${\displaystyle 8}$	${\displaystyle 24\left({\tfrac {\sqrt {2}}{3}}\right)\approx 11.314}$	${\displaystyle 600\left({\tfrac {\sqrt {2}}{12\phi ^{3}}}\right)\approx 16.693}$	${\displaystyle 120\left({\tfrac {15+7{\sqrt {5}}}{4\phi ^{6}{\sqrt {8}}}}\right)\approx 18.118}$
4-Content	${\displaystyle {\tfrac {\sqrt {5}}{24}}\left({\tfrac {\sqrt {5}}{2}}\right)^{4}\approx 0.146}$	${\displaystyle {\tfrac {2}{3}}\approx 0.667}$	${\displaystyle 1}$	${\displaystyle 2}$	${\displaystyle {\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 3.863}$	${\displaystyle {\tfrac {{\text{Short}}\times {\text{Vol}}}{4}}\approx 4.193}$

The following table lists some properties of the six convex regular 4-polytopes. The symmetry groups of these 4-polytopes are all Coxeter groups and given in the notation described in that article. The number following the name of the group is the order of the group.

Names	Image	Family	Schläfli Coxeter	V	E	F	C	Vert. fig.	Dual	Symmetry group
5-cell pentachoron pentatope 4-simplex		n-simplex (An family)	{3,3,3}	5	10	10 {3}	5 {3,3}	{3,3}	self-dual	A4 [3,3,3]	120
16-cell hexadecachoron 4-orthoplex		n-orthoplex (Bn family)	{3,3,4}	8	24	32 {3}	16 {3,3}	{3,4}	8-cell	B4 [4,3,3]	384
8-cell octachoron tesseract 4-cube		hypercube n-cube (Bn family)	{4,3,3}	16	32	24 {4}	8 {4,3}	{3,3}	16-cell
24-cell icositetrachoron octaplex polyoctahedron (pO)		Fn family	{3,4,3}	24	96	96 {3}	24 {3,4}	{4,3}	self-dual	F4 [3,4,3]	1152
600-cell hexacosichoron tetraplex polytetrahedron (pT)		n-pentagonal polytope (Hn family)	{3,3,5}	120	720	1200 {3}	600 {3,3}	{3,5}	120-cell	H4 [5,3,3]	14400
120-cell hecatonicosachoron dodecacontachoron dodecaplex polydodecahedron (pD)		n-pentagonal polytope (Hn family)	{5,3,3}	600	1200	720 {5}	120 {5,3}	{3,3}	600-cell

John Conway advocated the names simplex, orthoplex, tesseract, octaplex or polyoctahedron (pO), tetraplex or polytetrahedron (pT), and dodecaplex or polydodecahedron (pD).^[3]

Norman Johnson advocated the names n-cell, or pentachoron, hexadecachoron, tesseract or octachoron, icositetrachoron, hexacosichoron, and hecatonicosachoron (or dodecacontachoron), coining the term polychoron being a 4D analogy to the 3D polyhedron, and 2D polygon, expressed from the Greek roots poly ("many") and choros ("room" or "space").^[4][5]

The Euler characteristic for all 4-polytopes is zero, we have the 4-dimensional analogue of Euler's polyhedral formula:

${\displaystyle N_{0}-N_{1}+N_{2}-N_{3}=0\,}$

where N_k denotes the number of k-faces in the polytope (a vertex is a 0-face, an edge is a 1-face, etc.).

The topology of any given 4-polytope is defined by its Betti numbers and torsion coefficients.^[6]

As configurations

A regular 4-polytope can be completely described as a configuration matrix containing counts of its component elements. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers (upper left to lower right) say how many of each element occur in the whole 4-polytope. The non-diagonal numbers say how many of the column's element occur in or at the row's element. For example, there are 2 vertices in each edge (each edge has 2 vertices), and 2 cells meet at each face (each face belongs to 2 cells), in any regular 4-polytope. The configuration for the dual polytope can be obtained by rotating the matrix by 180 degrees.^[7][8]

5-cell {3,3,3}	16-cell {3,3,4}	8-cell {4,3,3}	24-cell {3,4,3}	600-cell {3,3,5}	120-cell {5,3,3}
${\displaystyle {\begin{bmatrix}{\begin{matrix}5&4&6&4\\2&10&3&3\\3&3&10&2\\4&6&4&5\end{matrix}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\begin{matrix}8&6&12&8\\2&24&4&4\\3&3&32&2\\4&6&4&16\end{matrix}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\begin{matrix}16&4&6&4\\2&32&3&3\\4&4&24&2\\8&12&6&8\end{matrix}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\begin{matrix}24&8&12&6\\2&96&3&3\\3&3&96&2\\6&12&8&24\end{matrix}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\begin{matrix}120&12&30&20\\2&720&5&5\\3&3&1200&2\\4&6&4&600\end{matrix}}\end{bmatrix}}}$	${\displaystyle {\begin{bmatrix}{\begin{matrix}600&4&6&4\\2&1200&3&3\\5&5&720&2\\20&30&12&120\end{matrix}}\end{bmatrix}}}$

Visualization

The following table shows some 2-dimensional projections of these 4-polytopes. Various other visualizations can be found in the external links below. The Coxeter-Dynkin diagram graphs are also given below the Schläfli symbol.

A4 = [3,3,3]	B4 = [4,3,3]		F4 = [3,4,3]	H4 = [5,3,3]
5-cell	16-cell	8-cell	24-cell	600-cell	120-cell
{3,3,3}	{3,3,4}	{4,3,3}	{3,4,3}	{3,3,5}	{5,3,3}
Solid 3D orthographic projections
Tetrahedral envelope (cell/vertex-centered)	Cubic envelope (cell-centered)	Cubic envelope (cell-centered)	Cuboctahedral envelope (cell-centered)	Pentakis icosidodecahedral envelope (vertex-centered)	Truncated rhombic triacontahedron envelope (cell-centered)
Wireframe Schlegel diagrams (Perspective projection)
Cell-centered	Cell-centered	Cell-centered	Cell-centered	Vertex-centered	Cell-centered
Wireframe stereographic projections (3-sphere)

Regular star (Schläfli–Hess) 4-polytopes

This shows the relationships among the four-dimensional starry polytopes. The 2 convex forms and 10 starry forms can be seen in 3D as the vertices of a cuboctahedron.^[9]

A subset of relations among 8 forms from the 120-cell, polydodecahedron (pD). The three operations {a,g,s} are commutable, defining a cubic framework. There are 7 densities seen in vertical positioning, with 2 dual forms having the same density.

The Schläfli–Hess 4-polytopes are the complete set of 10 regular self-intersecting star polychora (four-dimensional polytopes).^[10] They are named in honor of their discoverers: Ludwig Schläfli and Edmund Hess. Each is represented by a Schläfli symbol {p,q,r} in which one of the numbers is ⁠5/2⁠. They are thus analogous to the regular nonconvex Kepler–Poinsot polyhedra, which are in turn analogous to the pentagram.

Names

Their names given here were given by John Conway, extending Cayley's names for the Kepler–Poinsot polyhedra: along with stellated and great, he adds a grand modifier. Conway offered these operational definitions:

1. stellation – replaces edges with longer edges in same lines. (Example: a pentagon stellates into a pentagram)
2. greatening – replaces the faces with large ones in same planes. (Example: an icosahedron greatens into a great icosahedron)
3. aggrandizement – replaces the cells with large ones in same 3-spaces. (Example: a 600-cell aggrandizes into a grand 600-cell)

John Conway names the 10 forms from 3 regular celled 4-polytopes: pT=polytetrahedron {3,3,5} (a tetrahedral 600-cell), pI=polyicosahedron {3,5,⁠5/2⁠} (an icosahedral 120-cell), and pD=polydodecahedron {5,3,3} (a dodecahedral 120-cell), with prefix modifiers: g, a, and s for great, (ag)grand, and stellated. The final stellation, the great grand stellated polydodecahedron contains them all as gaspD.

Symmetry

All ten polychora have [3,3,5] (H₄) hexacosichoric symmetry. They are generated from 6 related Goursat tetrahedra rational-order symmetry groups: [3,5,5/2], [5,5/2,5], [5,3,5/2], [5/2,5,5/2], [5,5/2,3], and [3,3,5/2].

Each group has 2 regular star-polychora, except for two groups which are self-dual, having only one. So there are 4 dual-pairs and 2 self-dual forms among the ten regular star polychora.

Properties

Note:

• There are 2 unique vertex arrangements, matching those of the 120-cell and 600-cell.
• There are 4 unique edge arrangements, which are shown as wireframes orthographic projections.
• There are 7 unique face arrangements, shown as solids (face-colored) orthographic projections.

The cells (polyhedra), their faces (polygons), the polygonal edge figures and polyhedral vertex figures are identified by their Schläfli symbols.

Name Conway (abbrev.)	Orthogonal projection	Schläfli Coxeter	C {p, q}	F {p}	E {r}	V {q, r}	Dens.	χ
Icosahedral 120-cell polyicosahedron (pI)		{3,5,5/2}	120 {3,5}	1200 {3}	720 {5/2}	120 {5,5/2}	4	480
Small stellated 120-cell stellated polydodecahedron (spD)		{5/2,5,3}	120 {5/2,5}	720 {5/2}	1200 {3}	120 {5,3}	4	−480
Great 120-cell great polydodecahedron (gpD)		{5,5/2,5}	120 {5,5/2}	720 {5}	720 {5}	120 {5/2,5}	6	0
Grand 120-cell grand polydodecahedron (apD)		{5,3,5/2}	120 {5,3}	720 {5}	720 {5/2}	120 {3,5/2}	20	0
Great stellated 120-cell great stellated polydodecahedron (gspD)		{5/2,3,5}	120 {5/2,3}	720 {5/2}	720 {5}	120 {3,5}	20	0
Grand stellated 120-cell grand stellated polydodecahedron (aspD)		{5/2,5,5/2}	120 {5/2,5}	720 {5/2}	720 {5/2}	120 {5,5/2}	66	0
Great grand 120-cell great grand polydodecahedron (gapD)		{5,5/2,3}	120 {5,5/2}	720 {5}	1200 {3}	120 {5/2,3}	76	−480
Great icosahedral 120-cell great polyicosahedron (gpI)		{3,5/2,5}	120 {3,5/2}	1200 {3}	720 {5}	120 {5/2,5}	76	480
Grand 600-cell grand polytetrahedron (apT)		{3,3,5/2}	600 {3,3}	1200 {3}	720 {5/2}	120 {3,5/2}	191	0
Great grand stellated 120-cell great grand stellated polydodecahedron (gaspD)		{5/2,3,3}	120 {5/2,3}	720 {5/2}	1200 {3}	600 {3,3}	191	0

See also

• Regular polytope
• List of regular polytopes
• Infinite regular 4-polytopes:
  • One regular Euclidean honeycomb: {4,3,4}
  • Four compact regular hyperbolic honeycombs: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
  • Eleven paracompact regular hyperbolic honeycombs: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3,6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5}, and {6,3,6}.
• Abstract regular 4-polytopes:
  • 11-cell {3,5,3}
  • 57-cell {5,3,5}
• Uniform 4-polytope uniform 4-polytope families constructed from these 6 regular forms.
• Platonic solid
• Kepler-Poinsot polyhedra — regular star polyhedron
• Star polygon — regular star polygons
• 4-polytope
• 5-polytope
• 6-polytope

Notes

References

Citations

1. Coxeter 1973, p. 141, §7-x. Historical remarks.
2. Coxeter 1973, pp. 292–293, Table I(ii): The sixteen regular polytopes {p,q,r} in four dimensions.
3. Conway, Burgiel & Goodman-Strauss 2008, Ch. 26. Higher Still
4. "Convex and abstract polytopes", Programme and abstracts, MIT, 2005
5. Johnson, Norman W. (2018). "§ 11.5 Spherical Coxeter groups". Geometries and Transformations. Cambridge University Press. pp. 246–. ISBN 978-1-107-10340-5.
6. Richeson, David S. (2012). "23. Henri Poincaré and the Ascendancy of Topology". Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton University Press. pp. 256–. ISBN 978-0-691-15457-2.
7. Coxeter 1973, § 1.8 Configurations
8. Coxeter, Complex Regular Polytopes, p.117
9. Conway, Burgiel & Goodman-Strauss 2008, p. 406, Fig 26.2
10. Coxeter, Star polytopes and the Schläfli function f{α,β,γ) p. 122 2. The Schläfli-Hess polytopes

Bibliography

• Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (3rd ed.). New York: Dover.
• Coxeter, H.S.M. (1969). Introduction to Geometry (2nd ed.). Wiley. ISBN 0-471-50458-0.
• D.M.Y. Sommerville (2020) [1930]. "X. The Regular Polytopes". Introduction to the Geometry of n Dimensions. Courier Dover. pp. 159–192. ISBN 978-0-486-84248-6.
• Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "26. Regular Star-polytopes". The Symmetries of Things. pp. 404–8. ISBN 978-1-56881-220-5.
• Hess, Edmund (1883). "Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder".
• Hess, Edmund (1885). "Uber die regulären Polytope höherer Art". Sitzungsber Gesells Beförderung Gesammten Naturwiss Marburg: 31–57.
• Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic, eds. (1995). Kaleidoscopes: Selected Writings of H.S.M. Coxeter. Wiley. ISBN 978-0-471-01003-6.
  • (Paper 10) Coxeter, H.S.M. (1989). "Star Polytopes and the Schlafli Function f(α,β,γ)". Elemente der Mathematik. 44 (2): 25–36.
• Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge University Press. ISBN 978-0-521-39490-1.
• McMullen, Peter; Schulte, Egon (2002). "Abstract Regular Polytopes" (PDF).

External links

• Weisstein, Eric W. "Regular polychoron". MathWorld.
• Jonathan Bowers, 16 regular 4-polytopes
• Regular 4D Polytope Foldouts
• Catalog of Polytope Images A collection of stereographic projections of 4-polytopes.
• A Catalog of Uniform Polytopes
• Dimensions 2 hour film about the fourth dimension (contains stereographic projections of all regular 4-polytopes)
• Reguläre Polytope
• The Regular Star Polychora
• Hypersolids