Top Qs
Timeline
Chat
Perspective
Cantellated 5-simplexes
From Wikipedia, the free encyclopedia
Remove ads
In five-dimensional geometry, a cantellated 5-simplex is a convex uniform 5-polytope, being a cantellation of the regular 5-simplex.
There are unique 4 degrees of cantellation for the 5-simplex, including truncations.
Remove ads
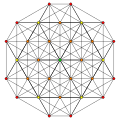
Cantellated 5-simplex
Summarize
Perspective
| Cantellated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | rr{3,3,3,3} = | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 27 | 6 r{3,3,3} 6 rr{3,3,3} 15 {}x{3,3} |
| Cells | 135 | 30 {3,3} 30 r{3,3} 15 rr{3,3} 60 {}x{3} |
| Faces | 290 | 200 {3} 90 {4} |
| Edges | 240 | |
| Vertices | 60 | |
| Vertex figure |  Tetrahedral prism | |
| Coxeter group | A5 [3,3,3,3], order 720 | |
| Properties | convex | |
The cantellated 5-simplex has 60 vertices, 240 edges, 290 faces (200 triangles and 90 squares), 135 cells (30 tetrahedra, 30 octahedra, 15 cuboctahedra and 60 triangular prisms), and 27 4-faces (6 cantellated 5-cell, 6 rectified 5-cells, and 15 tetrahedral prisms).
Alternate names
- Cantellated hexateron
- Small rhombated hexateron (Acronym: sarx) (Jonathan Bowers)[1]
Coordinates
The vertices of the cantellated 5-simplex can be most simply constructed on a hyperplane in 6-space as permutations of (0,0,0,1,1,2) or of (0,1,1,2,2,2). These represent positive orthant facets of the cantellated hexacross and bicantellated hexeract respectively.
Images
Remove ads
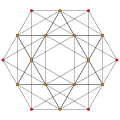
Bicantellated 5-simplex
Summarize
Perspective
| Bicantellated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | 2rr{3,3,3,3} = | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 32 | 12 t02{3,3,3} 20 {3}x{3} |
| Cells | 180 | 30 t1{3,3} 120 {}x{3} 30 t02{3,3} |
| Faces | 420 | 240 {3} 180 {4} |
| Edges | 360 | |
| Vertices | 90 | |
| Vertex figure |  | |
| Coxeter group | A5×2, [[3,3,3,3]], order 1440 | |
| Properties | convex, isogonal | |
Alternate names
- Bicantellated hexateron
- Small birhombated dodecateron (Acronym: sibrid) (Jonathan Bowers)[2]
Coordinates
The coordinates can be made in 6-space, as 90 permutations of:
- (0,0,1,1,2,2)
This construction exists as one of 64 orthant facets of the bicantellated 6-orthoplex.
Images
Remove ads
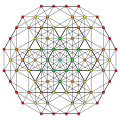
Cantitruncated 5-simplex
Summarize
Perspective
| cantitruncated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | tr{3,3,3,3} = | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 27 | 6 t012{3,3,3} 6 t{3,3,3} 15 {}x{3,3} |
| Cells | 135 | 15 t012{3,3} 30 t{3,3} 60 {}x{3} 30 {3,3} |
| Faces | 290 | 120 {3} 80 {6} 90 {}x{} |
| Edges | 300 | |
| Vertices | 120 | |
| Vertex figure | 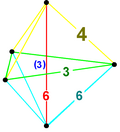 Irr. 5-cell | |
| Coxeter group | A5 [3,3,3,3], order 720 | |
| Properties | convex | |
Alternate names
- Cantitruncated hexateron
- Great rhombated hexateron (Acronym: garx) (Jonathan Bowers)[3]
Coordinates
The vertices of the cantitruncated 5-simplex can be most simply constructed on a hyperplane in 6-space as permutations of (0,0,0,1,2,3) or of (0,1,2,3,3,3). These construction can be seen as facets of the cantitruncated 6-orthoplex or bicantitruncated 6-cube respectively.
Images
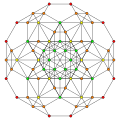
Bicantitruncated 5-simplex
Summarize
Perspective
| Bicantitruncated 5-simplex | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | 2tr{3,3,3,3} = | |
| Coxeter-Dynkin diagram | or | |
| 4-faces | 32 | 12 tr{3,3,3} 20 {3}x{3} |
| Cells | 180 | 30 t{3,3} 120 {}x{3} 30 t{3,4} |
| Faces | 420 | 240 {3} 180 {4} |
| Edges | 450 | |
| Vertices | 180 | |
| Vertex figure |  | |
| Coxeter group | A5×2, [[3,3,3,3]], order 1440 | |
| Properties | convex, isogonal | |
Alternate names
- Bicantitruncated hexateron
- Great birhombated dodecateron(Acronym: gibrid) (Jonathan Bowers)[4]
Coordinates
The coordinates can be made in 6-space, as 180 permutations of:
- (0,0,1,2,3,3)
This construction exists as one of 64 orthant facets of the bicantitruncated 6-orthoplex.
Images
Remove ads
Related uniform 5-polytopes
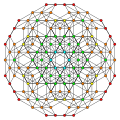
The cantellated 5-simplex is one of 19 uniform 5-polytopes based on the [3,3,3,3] Coxeter group, all shown here in A5 Coxeter plane orthographic projections. (Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)
Remove ads
Notes
References
External links
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
Remove ads