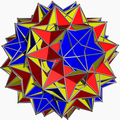
Great dirhombicosidodecahedron

In geometry, the great dirhombicosidodecahedron (or great snub disicosidisdodecahedron) is a nonconvex uniform polyhedron, indexed last as $U 75$ . It has 124 faces (40 triangles, 60 squares, and 24 pentagrams), 240 edges, and 60 vertices.^[1]

Great dirhombicosidodecahedron

Type	Uniform star polyhedron
Elements	F = 124, E = 240 V = 60 (χ = −56)
Faces by sides	40{3}+60{4}+24{5/2}
Coxeter diagram
Wythoff symbol	\| 3/2 5/3 3 5/2
Symmetry group	I_h, [5,3], *532
Index references	U₇₅, C₉₂, W₁₁₉
Dual polyhedron	Great dirhombicosidodecacron
Vertex figure	4.5/3.4.3.4.5/2.4.3/2
Bowers acronym	Gidrid

This is the only non-degenerate uniform polyhedron with more than six faces meeting at a vertex. Each vertex has 4 squares which pass through the vertex central axis (and thus through the centre of the figure), alternating with two triangles and two pentagrams. Another unusual feature is that the faces all occur in coplanar pairs.

This is also the only uniform polyhedron that cannot be made by the Wythoff construction from a spherical triangle. It has a special Wythoff symbol $| .mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}3⁄2 5⁄3 3 5⁄2,$ relating it to a spherical quadrilateral. This symbol suggests that it is a sort of snub polyhedron, except that instead of the non-snub faces being surrounded by snub triangles as in most snub polyhedra, they are surrounded by snub squares.

It has been nicknamed "Miller's monster" (after J. C. P. Miller, who with H. S. M. Coxeter and M. S. Longuet-Higgins enumerated the uniform polyhedra in 1954).

If the definition of a uniform polyhedron is relaxed to allow any even number of faces adjacent to an edge, then this definition gives rise to one further polyhedron: the great disnub dirhombidodecahedron which has the same vertices and edges but with a different arrangement of triangular faces.

The vertices and edges are also shared with the uniform compounds of 20 octahedra or 20 tetrahemihexahedra. 180 of the 240 edges are shared with the great snub dodecicosidodecahedron.

Convex hull	Great snub dodecicosidodecahedron	Great dirhombicosidodecahedron
Great disnub dirhombidodecahedron	Compound of twenty octahedra	Compound of twenty tetrahemihexahedra

This polyhedron is related to the nonconvex great rhombicosidodecahedron (quasirhombicosidodecahedron) by a branched cover: there is a function from the great dirhombicosidodecahedron to the quasirhombicosidodecahedron that is 2-to-1 everywhere, except for the vertices.^[2]

Let the point $p$ be given by

p={\begin{pmatrix}\phi ^{-{\frac {1}{2}}}\\0\\\phi ^{-1}\end{pmatrix}}

,

where $\phi$ is the golden ratio. Let the matrix $M$ be given by

M={\begin{pmatrix}1/2&-\phi /2&1/(2\phi )\\\phi /2&1/(2\phi )&-1/2\\1/(2\phi )&1/2&\phi /2\end{pmatrix}}

.

$M$ is the rotation around the axis $(1,0,\phi )$ by an angle of $2\pi /5$ , counterclockwise. Let the linear transformations $T_{0},\ldots ,T_{11}$ be the transformations which send a point $(x,y,z)$ to the even permutations of $(\pm x,\pm y,\pm z)$ with an even number of minus signs. The transformations $T_{i}$ constitute the group of rotational symmetries of a regular tetrahedron. The transformations $T_{i}M^{j}$ $(i=0,\ldots ,11$ , $j=0,\ldots ,4)$ constitute the group of rotational symmetries of a regular icosahedron. Then the 60 points $T_{i}M^{j}p$ are the vertices of a great dirhombicosidodecahedron. The edge length equals ${\sqrt {2}}$ , the circumradius equals $1$ , and the midradius equals ${\frac {1}{2}}{\sqrt {2}}$ .