Loading AI tools
Type of climate model From Wikipedia, the free encyclopedia
A general circulation model (GCM) is a type of climate model. It employs a mathematical model of the general circulation of a planetary atmosphere or ocean. It uses the Navier–Stokes equations on a rotating sphere with thermodynamic terms for various energy sources (radiation, latent heat). These equations are the basis for computer programs used to simulate the Earth's atmosphere or oceans. Atmospheric and oceanic GCMs (AGCM and OGCM) are key components along with sea ice and land-surface components.
GCMs and global climate models are used for weather forecasting, understanding the climate, and forecasting climate change.
Atmospheric GCMs (AGCMs) model the atmosphere and impose sea surface temperatures as boundary conditions. Coupled atmosphere-ocean GCMs (AOGCMs, e.g. HadCM3, EdGCM, GFDL CM2.X, ARPEGE-Climat)[2] combine the two models. The first general circulation climate model that combined both oceanic and atmospheric processes was developed in the late 1960s at the NOAA Geophysical Fluid Dynamics Laboratory[3] AOGCMs represent the pinnacle of complexity in climate models and internalise as many processes as possible. However, they are still under development and uncertainties remain. They may be coupled to models of other processes, such as the carbon cycle, so as to better model feedback effects. Such integrated multi-system models are sometimes referred to as either "earth system models" or "global climate models."
Versions designed for decade to century time scale climate applications were originally created by Syukuro Manabe and Kirk Bryan at the Geophysical Fluid Dynamics Laboratory (GFDL) in Princeton, New Jersey.[1] These models are based on the integration of a variety of fluid dynamical, chemical and sometimes biological equations.
The acronym GCM originally stood for General Circulation Model. Recently, a second meaning came into use, namely Global Climate Model. While these do not refer to the same thing, General Circulation Models are typically the tools used for modelling climate, and hence the two terms are sometimes used interchangeably. However, the term "global climate model" is ambiguous and may refer to an integrated framework that incorporates multiple components including a general circulation model, or may refer to the general class of climate models that use a variety of means to represent the climate mathematically.
Atmospheric (AGCMs) and oceanic GCMs (OGCMs) can be coupled to form an atmosphere-ocean coupled general circulation model (CGCM or AOGCM). With the addition of submodels such as a sea ice model or a model for evapotranspiration over land, AOGCMs become the basis for a full climate model.[4]
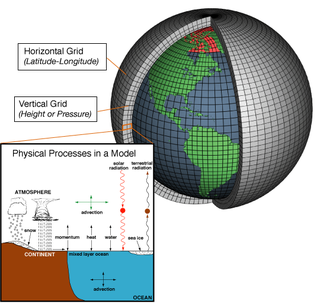
General Circulation Models (GCMs) discretise the equations for fluid motion and energy transfer and integrate these over time. Unlike simpler models, GCMs divide the atmosphere and/or oceans into grids of discrete "cells", which represent computational units. Unlike simpler models which make mixing assumptions, processes internal to a cell—such as convection—that occur on scales too small to be resolved directly are parameterised at the cell level, while other functions govern the interface between cells.
Three-dimensional (more properly four-dimensional) GCMs apply discrete equations for fluid motion and integrate these forward in time. They contain parameterisations for processes such as convection that occur on scales too small to be resolved directly.
A simple general circulation model (SGCM) consists of a dynamic core that relates properties such as temperature to others such as pressure and velocity. Examples are programs that solve the primitive equations, given energy input and energy dissipation in the form of scale-dependent friction, so that atmospheric waves with the highest wavenumbers are most attenuated. Such models may be used to study atmospheric processes, but are not suitable for climate projections.
Atmospheric GCMs (AGCMs) model the atmosphere (and typically contain a land-surface model as well) using imposed sea surface temperatures (SSTs).[5] They may include atmospheric chemistry.
AGCMs consist of a dynamical core which integrates the equations of fluid motion, typically for:
A GCM contains prognostic equations that are a function of time (typically winds, temperature, moisture, and surface pressure) together with diagnostic equations that are evaluated from them for a specific time period. As an example, pressure at any height can be diagnosed by applying the hydrostatic equation to the predicted surface pressure and the predicted values of temperature between the surface and the height of interest. Pressure is used to compute the pressure gradient force in the time-dependent equation for the winds.
OGCMs model the ocean (with fluxes from the atmosphere imposed) and may contain a sea ice model. For example, the standard resolution of HadOM3 is 1.25 degrees in latitude and longitude, with 20 vertical levels, leading to approximately 1,500,000 variables.
AOGCMs (e.g. HadCM3, GFDL CM2.X) combine the two submodels. They remove the need to specify fluxes across the interface of the ocean surface. These models are the basis for model predictions of future climate, such as are discussed by the IPCC. AOGCMs internalise as many processes as possible. They have been used to provide predictions at a regional scale. While the simpler models are generally susceptible to analysis and their results are easier to understand, AOGCMs may be nearly as hard to analyse as the climate itself.
The fluid equations for AGCMs are made discrete using either the finite difference method or the spectral method. For finite differences, a grid is imposed on the atmosphere. The simplest grid uses constant angular grid spacing (i.e., a latitude / longitude grid). However, non-rectangular grids (e.g., icosahedral) and grids of variable resolution [6] are more often used.[7] The LMDz model can be arranged to give high resolution over any given section of the planet. HadGEM1 (and other ocean models) use an ocean grid with higher resolution in the tropics to help resolve processes believed to be important for the El Niño Southern Oscillation (ENSO). Spectral models generally use a gaussian grid, because of the mathematics of transformation between spectral and grid-point space. Typical AGCM resolutions are between 1 and 5 degrees in latitude or longitude: HadCM3, for example, uses 3.75 in longitude and 2.5 degrees in latitude, giving a grid of 96 by 73 points (96 x 72 for some variables); and has 19 vertical levels. This results in approximately 500,000 "basic" variables, since each grid point has four variables (u,v, T, Q), though a full count would give more (clouds; soil levels). HadGEM1 uses a grid of 1.875 degrees in longitude and 1.25 in latitude in the atmosphere; HiGEM, a high-resolution variant, uses 1.25 x 0.83 degrees respectively.[8] These resolutions are lower than is typically used for weather forecasting.[9] Ocean resolutions tend to be higher, for example HadCM3 has 6 ocean grid points per atmospheric grid point in the horizontal.
For a standard finite difference model, uniform gridlines converge towards the poles. This would lead to computational instabilities (see CFL condition) and so the model variables must be filtered along lines of latitude close to the poles. Ocean models suffer from this problem too, unless a rotated grid is used in which the North Pole is shifted onto a nearby landmass. Spectral models do not suffer from this problem. Some experiments use geodesic grids[10] and icosahedral grids, which (being more uniform) do not have pole-problems. Another approach to solving the grid spacing problem is to deform a Cartesian cube such that it covers the surface of a sphere.[11]
Some early versions of AOGCMs required an ad hoc process of "flux correction" to achieve a stable climate. This resulted from separately prepared ocean and atmospheric models that each used an implicit flux from the other component different than that component could produce. Such a model failed to match observations. However, if the fluxes were 'corrected', the factors that led to these unrealistic fluxes might be unrecognised, which could affect model sensitivity. As a result, the vast majority of models used in the current round of IPCC reports do not use them. The model improvements that now make flux corrections unnecessary include improved ocean physics, improved resolution in both atmosphere and ocean, and more physically consistent coupling between atmosphere and ocean submodels. Improved models now maintain stable, multi-century simulations of surface climate that are considered to be of sufficient quality to allow their use for climate projections.[12]
Moist convection releases latent heat and is important to the Earth's energy budget. Convection occurs on too small a scale to be resolved by climate models, and hence it must be handled via parameters. This has been done since the 1950s. Akio Arakawa did much of the early work, and variants of his scheme are still used,[13] although a variety of different schemes are now in use.[14][15][16] Clouds are also typically handled with a parameter, for a similar lack of scale. Limited understanding of clouds has limited the success of this strategy, but not due to some inherent shortcoming of the method.[17]
Most models include software to diagnose a wide range of variables for comparison with observations or study of atmospheric processes. An example is the 2-metre temperature, which is the standard height for near-surface observations of air temperature. This temperature is not directly predicted from the model but is deduced from surface and lowest-model-layer temperatures. Other software is used for creating plots and animations.
Coupled AOGCMs use transient climate simulations to project/predict climate changes under various scenarios. These can be idealised scenarios (most commonly, CO2 emissions increasing at 1%/yr) or based on recent history (usually the "IS92a" or more recently the SRES scenarios). Which scenarios are most realistic remains uncertain.
The 2001 IPCC Third Assessment Report Figure 9.3 shows the global mean response of 19 different coupled models to an idealised experiment in which emissions increased at 1% per year.[19] Figure 9.5 shows the response of a smaller number of models to more recent trends. For the 7 climate models shown there, the temperature change to 2100 varies from 2 to 4.5 °C with a median of about 3 °C.
Future scenarios do not include unknown events – for example, volcanic eruptions or changes in solar forcing. These effects are believed to be small in comparison to greenhouse gas (GHG) forcing in the long term, but large volcanic eruptions, for example, can exert a substantial temporary cooling effect.
Human GHG emissions are a model input, although it is possible to include an economic/technological submodel to provide these as well. Atmospheric GHG levels are usually supplied as an input, though it is possible to include a carbon cycle model that reflects vegetation and oceanic processes to calculate such levels.
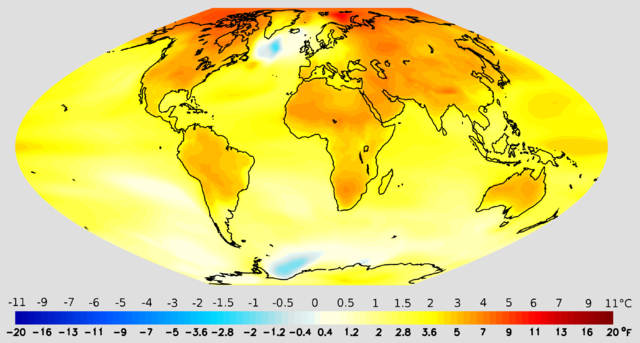
For the six SRES marker scenarios, IPCC (2007:7–8) gave a "best estimate" of global mean temperature increase (2090–2099 relative to the period 1980–1999) of 1.8 °C to 4.0 °C.[20] Over the same time period, the "likely" range (greater than 66% probability, based on expert judgement) for these scenarios was for a global mean temperature increase of 1.1 to 6.4 °C.[20]
In 2008 a study made climate projections using several emission scenarios.[21] In a scenario where global emissions start to decrease by 2010 and then declined at a sustained rate of 3% per year, the likely global average temperature increase was predicted to be 1.7 °C above pre-industrial levels by 2050, rising to around 2 °C by 2100. In a projection designed to simulate a future where no efforts are made to reduce global emissions, the likely rise in global average temperature was predicted to be 5.5 °C by 2100. A rise as high as 7 °C was thought possible, although less likely.
Another no-reduction scenario resulted in a median warming over land (2090–99 relative to the period 1980–99) of 5.1 °C. Under the same emissions scenario but with a different model, the predicted median warming was 4.1 °C.[22]
This section needs to be updated. (August 2015) |



AOGCMs internalise as many processes as are sufficiently understood. However, they are still under development and significant uncertainties remain. They may be coupled to models of other processes in Earth system models, such as the carbon cycle, so as to better model feedbacks. Most recent simulations show "plausible" agreement with the measured temperature anomalies over the past 150 years, when driven by observed changes in greenhouse gases and aerosols. Agreement improves by including both natural and anthropogenic forcings.[23][24][25]
Imperfect models may nevertheless produce useful results. GCMs are capable of reproducing the general features of the observed global temperature over the past century.[23]
A debate over how to reconcile climate model predictions that upper air (tropospheric) warming should be greater than observed surface warming, some of which appeared to show otherwise,[26] was resolved in favour of the models, following data revisions.
Cloud effects are a significant area of uncertainty in climate models. Clouds have competing effects on climate. They cool the surface by reflecting sunlight into space; they warm it by increasing the amount of infrared radiation transmitted from the atmosphere to the surface.[27] In the 2001 IPCC report possible changes in cloud cover were highlighted as a major uncertainty in predicting climate.[28][29]
Climate researchers around the world use climate models to understand the climate system. Thousands of papers have been published about model-based studies. Part of this research is to improve the models.
In 2000, a comparison between measurements and dozens of GCM simulations of ENSO-driven tropical precipitation, water vapor, temperature, and outgoing longwave radiation found similarity between measurements and simulation of most factors. However the simulated change in precipitation was about one-fourth less than what was observed. Errors in simulated precipitation imply errors in other processes, such as errors in the evaporation rate that provides moisture to create precipitation. The other possibility is that the satellite-based measurements are in error. Either indicates progress is required in order to monitor and predict such changes.[30]
The precise magnitude of future changes in climate is still uncertain;[31] for the end of the 21st century (2071 to 2100), for SRES scenario A2, the change of global average SAT change from AOGCMs compared with 1961 to 1990 is +3.0 °C (5.4 °F) and the range is +1.3 to +4.5 °C (+2.3 to 8.1 °F).
The IPCC's Fifth Assessment Report asserted "very high confidence that models reproduce the general features of the global-scale annual mean surface temperature increase over the historical period". However, the report also observed that the rate of warming over the period 1998–2012 was lower than that predicted by 111 out of 114 Coupled Model Intercomparison Project climate models.[32]
The global climate models used for climate projections are similar in structure to (and often share computer code with) numerical models for weather prediction, but are nonetheless logically distinct.
Most weather forecasting is done on the basis of interpreting numerical model results. Since forecasts are typically a few days or a week and sea surface temperatures change relatively slowly, such models do not usually contain an ocean model but rely on imposed SSTs. They also require accurate initial conditions to begin the forecast – typically these are taken from the output of a previous forecast, blended with observations. Weather predictions are required at higher temporal resolutions than climate projections, often sub-hourly compared to monthly or yearly averages for climate. However, because weather forecasts only cover around 10 days the models can also be run at higher vertical and horizontal resolutions than climate mode. Currently the ECMWF runs at 9 km (5.6 mi) resolution[33] as opposed to the 100-to-200 km (62-to-124 mi) scale used by typical climate model runs. Often local models are run using global model results for boundary conditions, to achieve higher local resolution: for example, the Met Office runs a mesoscale model with an 11 km (6.8 mi) resolution[34] covering the UK, and various agencies in the US employ models such as the NGM and NAM models. Like most global numerical weather prediction models such as the GFS, global climate models are often spectral models[35] instead of grid models. Spectral models are often used for global models because some computations in modeling can be performed faster, thus reducing run times.
Climate models use quantitative methods to simulate the interactions of the atmosphere, oceans, land surface and ice.
All climate models take account of incoming energy as short wave electromagnetic radiation, chiefly visible and short-wave (near) infrared, as well as outgoing energy as long wave (far) infrared electromagnetic radiation from the earth. Any imbalance results in a change in temperature.
The most talked-about models of recent years relate temperature to emissions of greenhouse gases. These models project an upward trend in the surface temperature record, as well as a more rapid increase in temperature at higher altitudes.[36]
Three (or more properly, four since time is also considered) dimensional GCM's discretise the equations for fluid motion and energy transfer and integrate these over time. They also contain parametrisations for processes such as convection that occur on scales too small to be resolved directly.
Atmospheric GCMs (AGCMs) model the atmosphere and impose sea surface temperatures as boundary conditions. Coupled atmosphere-ocean GCMs (AOGCMs, e.g. HadCM3, EdGCM, GFDL CM2.X, ARPEGE-Climat[37]) combine the two models.
Models range in complexity:
Other submodels can be interlinked, such as land use, allowing researchers to predict the interaction between climate and ecosystems.
The Climber-3 model uses a 2.5-dimensional statistical-dynamical model with 7.5° × 22.5° resolution and time step of 1/2 a day. An oceanic submodel is MOM-3 (Modular Ocean Model) with a 3.75° × 3.75° grid and 24 vertical levels.[38]
One-dimensional, radiative-convective models were used to verify basic climate assumptions in the 1980s and 1990s.[39]
GCMs can form part of Earth system models, e.g. by coupling ice sheet models for the dynamics of the Greenland and Antarctic ice sheets, and one or more chemical transport models (CTMs) for species important to climate. Thus a carbon chemistry transport model may allow a GCM to better predict anthropogenic changes in carbon dioxide concentrations. In addition, this approach allows accounting for inter-system feedback: e.g. chemistry-climate models allow the effects of climate change on the ozone hole to be studied.[40]
In 1956, Norman Phillips developed a mathematical model that could realistically depict monthly and seasonal patterns in the troposphere. It became the first successful climate model.[41][42] Following Phillips's work, several groups began working to create GCMs.[43] The first to combine both oceanic and atmospheric processes was developed in the late 1960s at the NOAA Geophysical Fluid Dynamics Laboratory.[1] By the early 1980s, the United States' National Center for Atmospheric Research had developed the Community Atmosphere Model; this model has been continuously refined.[44] In 1996, efforts began to model soil and vegetation types.[45] Later the Hadley Centre for Climate Prediction and Research's HadCM3 model coupled ocean-atmosphere elements.[43] The role of gravity waves was added in the mid-1980s. Gravity waves are required to simulate regional and global scale circulations accurately.[46]
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.