Κύκλος

Για άλλες χρήσεις, δείτε: Κύκλος (αποσαφήνιση).

Στην γεωμετρία, κύκλος ή περιφέρεια με κέντρο το σημείο ${\displaystyle {\rm {O}}}$ και ακτίνα ${\displaystyle \rho }$, ονομάζεται το γεωμετρικό σχήμα που αποτελείται από όλα τα σημεία του επιπέδου τα οποία απέχουν από το ${\displaystyle {\rm {O}}}$ απόσταση ίση με ${\displaystyle \rho }$, και συμβολίζεται ${\displaystyle C(\mathrm {O} ,\rho )}$.^[1][2]

Σχήμα 1: Κύκλος με κέντρο ${\displaystyle {\rm {O}}}$ και ακτίνα ${\displaystyle \rho }$.

Ισοδύναμα ο κύκλος είναι ο γεωμετρικός τόπος των σημείων του επιπέδου που ισαπέχουν από ένα δεδομένο σημείο.

Διάμετρος ενός κύκλου ονομάζεται οποιοδήποτε ευθύγραμμο τμήμα διέρχεται από το κέντρο του κύκλου και τα άκρα του είναι σημεία του κύκλου.

Η διάμετρος ${\displaystyle \delta }$ ενός κύκλου είναι διπλάσια της ακτίνας, ${\displaystyle \delta =2\rho }$. Τα άκρα μιας διαμέτρου ονομάζονται αντιδιαμετρικά σημεία του κύκλου.

Σχήμα 2: Το εσωτερικό και το εξωτερικό του κύκλου.

Ένα σημείο ${\displaystyle {\rm {M}}}$ του επιπέδου του κύκλου ${\displaystyle C(\mathrm {O} ,\rho )}$ λέγεται εσωτερικό του κύκλου αν ισχύει ${\displaystyle \mathrm {MO} <\rho }$ και εξωτερικό του αν ισχύει ${\displaystyle \mathrm {MO} >\rho }$. Το σύνολο των εσωτερικών σημείων του κύκλου ${\displaystyle C(\mathrm {O} ,\rho )}$ ονομάζεται εσωτερικό του κύκλου, και το εσωτερικό μαζί με τον κύκλο ονομάζεται κυκλικός δίσκος.

Ο Ευκλείδης στο πρώτο βιβλίο των Στοιχείων (ορ. 15 -16) αναφέρει:

"Ο κύκλος είναι ένα επίπεδο σχήμα που περικλείεται από μια γραμμή (που λέγεται περιφέρεια) για την οποία υπάρχει ένα σημείο μέσα στο σχήμα από όπου κάθε δύο ευθύγραμμα τμήματα με το ένα άκρο στο σημείο αυτό και το άλλο άκρο στην περιφέρεια είναι ίσα. Αυτό το σημείο λέγεται κέντρο του κύκλου."

Δηλαδή, ο Ευκλείδης ταυτίζει τον κύκλο με τον κυκλικό δίσκο. Για αυτό το λόγο εμφανίζεται ο όρος περιφέρεια. Με άλλα λόγια οι λέξεις περιφέρεια και κύκλος περιέγραφαν παλαιότερα αυτά που σε σημερινή ορολογία λέμε κύκλος και κυκλικός δίσκος αντίστοιχα.

Στην Ευκλείδεια γεωμετρία, ίσοι ονομάζονται δύο κύκλοι οι οποίοι έχουν ίσες ακτίνες.

Τόξο, χορδή, επίκεντρη γωνία

Σχήμα 3: Χορδή ${\displaystyle {\rm {AB}}}$ και διάμετρος ${\displaystyle \Gamma \Delta }$.

Χορδή ενός κύκλου λέγεται το ευθύγραμμο τμήμα που ενώνει δύο σημεία του κύκλου.^{[3]: 49 [4]:34}

Σχήμα 4α: Επίκεντρη γωνία ${\displaystyle \angle {\rm {AOB}}}$, το αντίστοιχο τόξο της και ο κυκλικός της τομέας.

Σχήμα 4β: Εγγεγραμμένη γωνία ${\displaystyle \angle {\rm {AB\Gamma }}}$.

Επίκεντρη γωνία ενός κύκλου ${\displaystyle C(\mathrm {O} ,\rho )}$ λέγεται κάθε γωνία η οποία έχει κορυφή το κέντρο ${\displaystyle {\rm {O}}}$ του κύκλου.^{[3]:51[4]:38-39}

Εγγεγραμμένη γωνία σε κύκλο ${\displaystyle C(\mathrm {O} ,\rho )}$ λέγεται η γωνία που έχει τη κορυφή της στον κύκλο και οι πλευρές της τέμνουν τον κύκλο.

Για κάθε εγγεγραμμένη γωνία ${\displaystyle {\widehat {\rm {AB\Gamma }}}}$ σε κύκλο με κέντρο ${\displaystyle {\rm {O}}}$, η αντίστοιχη επίκεντρη γωνία ${\displaystyle {\rm {\widehat {AO\Gamma }}}}$ είναι διπλάσια.

Σχήμα 5α: Έλασσον τόξο ${\displaystyle {\rm {AB}}}$ και η αντίστοιχη κυρτή επίκεντρη γωνία του.

Σχήμα 5β: Μείζον τόξο ${\displaystyle {\rm {AB}}}$ και η αντίστοιχη μη-κυρτή επίκεντρη γωνία του.

Τόξο ενός κύκλου λέγεται το γεωμετρικό σχήμα που αποτελείται από τα κοινά σημεία του κύκλου και μιας επίκεντρης γωνίας του.

Στον ίδιο κύκλο ή σε ίσους κύκλους, σε ίσα τόξα αντιστοιχούν ίσες χορδές και αντίστροφα.

Στον ίδιο κύκλο ή σε ίσους κύκλους, σε ίσα τόξα αντιστοιχούν ίσες επίκεντρες γωνίες και αντίστροφα.

Κάθε ζεύγος σημείων πάνω σε έναν κύκλο ορίζει μία κυρτή και μία μη κυρτή επίκεντρη γωνία, άρα και δύο τόξα, το έλασσον και το μείζον αντίστοιχα.^{[5]: 50 [3]: 49}

Στο σχήμα 5α, αντίστοιχο τόξο της επίκεντρης γωνίας ${\displaystyle {\widehat {\rm {AOB}}}}$ θα λέμε το έλασσον τόξο ${\displaystyle {\rm {AB}}}$. Λέμε επίσης ότι η γωνία ${\displaystyle {\widehat {\rm {AOB}}}}$ βαίνει στο τόξο ${\displaystyle {\rm {AB}}}$, και ότι το τόξο ${\displaystyle {\rm {AB}}}$ φαίνεται υπό γωνία ${\displaystyle {\widehat {\rm {AOB}}}}$.

Ημικύκλιο λέγεται ένα τόξο που αντιστοιχεί σε μία επίκεντρη γωνία ${\displaystyle 180^{\circ }}$.

Σχήμα 6α: Κυκλικός τομέας ${\displaystyle {\rm {AOB}}}$.

Σχήμα 6β: Κυκλικό τμήμα ${\displaystyle {\rm {AOB}}}$.

Κυκλικός τομέας λέγεται το γεωμετρικό σχήμα που αποτελείται από τα κοινά σημεία ενός κυκλικού δίσκου και μίας επίκεντρης γωνίας του, όπως είναι το γραμμοσκιασμένο σύνολο του σχήματος 6α.

Κυκλικό τμήμα λέγεται το γεωμετρικό σχήμα που αποτελείται από τα σημεία μεταξύ ενός τόξου και μίας χορδής που αντιστοιχούν στην ίδια επίκεντρη γωνία. όπως είναι το γραμμοσκιασμένο σύνολο του σχήματος 6β.

Περίμετρος

Εάν ${\displaystyle L}$ είναι η περίμετρος του κύκλου, τότε:

${\displaystyle L=2\pi \rho }$,

όπου ${\displaystyle \pi \,\approx 3,14\ldots }$ η μαθηματική σταθερά.

Εμβαδόν

• Το εμβαδόν του κυκλικού δίσκου δίνεται από τον τύπο: ${\displaystyle {\rm {E}}=\pi \rho ^{2}}$.
• Ο κύκλος είναι το σχήμα του επιπέδου με το μεγαλύτερο εμβαδόν για δεδομένη περίμετρο.

Σχετικές θέσεις σημείου και κύκλου

Έστω ένα σημείο ${\displaystyle {\rm {P}}}$ και ένας κύκλος ${\displaystyle ({\rm {O}},\rho )}$. Το σημείο μπορεί να βρίσκεται^[5]:51

• μέσα στον κύκλο, δηλαδή ${\displaystyle {\rm {OP}}<\rho }$ και λέμε ότι είναι εσωτερικό σημείο του κύκλου (κανένα κοινό σημείο, «συνάφεια»)
• πάνω στον κύκλο, δηλαδή ${\displaystyle {\rm {OP}}=\rho }$ (ένα κοινό σημείο)
• έξω από τον κύκλο, δηλαδή ${\displaystyle {\rm {OP}}>\rho }$ και λέμε ότι είναι εξωτερικό σημείο του κύκλου (κανένα κοινό σημείο, μη «συνάφεια»)

Το ${\displaystyle {\rm {P}}}$ είναι εσωτερικό του κύκλου.

Το ${\displaystyle {\rm {P}}}$ είναι ανήκει στον κύκλο.

Το ${\displaystyle {\rm {P}}}$ είναι εξωτερικό του κύκλου.

Σχετικές θέσεις ευθείας και κύκλου

Έστω μία ευθεία ${\displaystyle \varepsilon }$ και ένας κύκλος ${\displaystyle ({\rm {O}},\rho )}$, και ${\displaystyle \delta }$ η μεταξύ τους απόσταση. Η ευθεία μπορεί να^[5]: 51

• τέμνει τον κύκλο, όταν ${\displaystyle \delta <\rho }$ και λέμε ότι είναι τέμνουσα του κύκλου (δύο κοινά σημεία),
• εφάπτεται στον στον κύκλο, όταν ${\displaystyle \delta =\rho }$ και λέμε ότι είναι εφαπτόμενη του κύκλου (ένα κοινό σημείο),
• βρίσκεται έξω από τον κύκλο, όταν ${\displaystyle \delta >\rho }$ και λέμε ότι είναι εξωτερική του κύκλου (κανένα κοινό σημείο).

Η ${\displaystyle \varepsilon }$ τέμνει τον ${\displaystyle ({\rm {O}},\rho )}$.

Η ${\displaystyle \varepsilon }$ εφάπτεται του ${\displaystyle ({\rm {O}},\rho )}$.

Η ${\displaystyle \varepsilon }$ είναι εξωτερική του ${\displaystyle ({\rm {O}},R)}$.

Σχετικές θέσεις δύο κύκλων

Δύο κύκλοι με κέντρα ${\displaystyle {\rm {O_{1},O_{2}}}}$, που είναι στο ίδιο επίπεδο μπορεί^{[5]: 51 [3]: 57-58}

• ταυτίζονται (άπειρα κοινά σημεία)
• τέμνονται (δύο κοινά σημεία)
• εφάπτονται εξωτερικά (ένα κοινό σημείο, μη «συνάφεια»)
• εφάπτονται εσωτερικά (ένα κοινό σημείο, «συνάφεια»)
• βρίσκονται ο ένας έξω από τον άλλο (κανένα κοινό σημείο, μη «συνάφεια»)
• βρίσκονται ο ένας μέσα στον άλλο (κανένα κοινό σημείο, «συνάφεια»)

Τέμνονται.

Εφάπτονται εσωτερικά.

Εφάπτονται εξωτερικά.

Ο ένας είναι εσωτερικός του άλλου.

Ο ένας είναι εξωτερικός του άλλου.

Δύναμη σημείου ως προς κύκλο

Κύριο λήμμα: Δύναμη σημείου ως προς κύκλο

Έστω ο κύκλος ${\displaystyle C(\mathrm {O} ,\rho )}$ και σημείο ${\displaystyle {\rm {P}}}$ του επιπέδου του. Αν ${\displaystyle {\rm {\varepsilon }}}$ είναι μια ευθεία που διέρχεται από το ${\displaystyle {\rm {P}}}$ και τέμνει τον κύκλο στα σημεία ${\displaystyle {\rm {A}}}$, ${\displaystyle {\rm {B}}}$ τότε το γινόμενο ${\displaystyle {\rm {PA\cdot PB}}}$ είναι σταθερό ανεξάρτητο της ευθείας ${\displaystyle {\rm {\epsilon }}}$. Το σταθερό γινόμενο ${\displaystyle {\rm {PA\cdot PB}}}$ ονομάζεται δύναμη του σημείου ${\displaystyle {\rm {P}}}$ ως προς τον κύκλο ${\displaystyle C}$.<^{[3]: 211-213 [6][7][8]}

Αν ${\displaystyle \delta }$ το μήκος του ευθυγράμμου τμήματος ${\displaystyle {\rm {OP}}}$ και ${\displaystyle \rho }$ η ακτίνα του κύκλου ${\displaystyle C(\mathrm {O} ,\rho )}$ ονομάζουμε δύναμη του ${\displaystyle {\rm {P}}}$ ως προς τον ${\displaystyle C}$ την διαφορά ${\displaystyle \delta ^{2}-\rho ^{2}}$ και την συμβολίζουμε με ${\displaystyle \Delta _{C}^{P}}$.

Αναλυτική γεωμετρία του κύκλου

Η εξίσωση, σε Καρτεσιανές συντεταγμένες, του κύκλου με κέντρο ${\displaystyle O(x_{0},y_{0})}$ και ακτίνα ${\displaystyle \rho >0}$ είναι:

${\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}=\rho ^{2}}$.

Όταν ο κύκλος έχει κέντρο την αρχή των αξόνων τότε η εξίσωση του κύκλου έχει τη μορφή :

${\displaystyle x^{2}+y^{2}=\rho ^{2}}$.

Η εξίσωση

${\displaystyle x^{2}+y^{2}+Ax+By+C=0}$,

όταν ${\displaystyle A^{2}+B^{2}-4C>0}$, αναπαριστά έναν κύκλο με κέντρο το σημείο ${\textstyle K(-{\tfrac {A}{2}},-{\tfrac {B}{2}})}$ και ακτίνα ${\textstyle \rho ={\tfrac {1}{2}}{\sqrt {A^{2}+B^{2}-4C}}}$.

Εξίσωση εφαπτομένης

Η εφαπτομένη του κύκλου αυτού σε ένα σημείο ${\displaystyle (x_{1},y_{1})}$ έχει εξίσωση της μορφής :

${\displaystyle xx_{1}+yy_{1}=\rho \,^{2}}$.

Παραμετρική εξίσωση

Οι παραμετρικές εξισώσεις του κύκλου είναι:

${\displaystyle x=x_{0}+\rho \cos t,\quad y=y_{0}+\rho \sin t}$,

με παράμετρο το ${\displaystyle t}$, για ${\displaystyle 0\leq t<2\pi }$.

Πολικές συντεταγμένες

Η εξίσωση ενός κύκλου σε πολικές συντεταγμένες με κέντρο το ${\displaystyle \,(r_{0},\phi _{0})}$ είναι:

${\displaystyle r^{2}-2r\,r_{0}\cos(\phi -\phi _{0})+r_{0}^{2}=\rho ^{2}.}$

Μιγαδικό επίπεδο

Στο μιγαδικό επίπεδο, ο κύκλος με κέντρο το ${\displaystyle (x_{0},y_{0})}$ και ακτίνα ${\displaystyle \rho }$ δίνεται από όλα τα σημεία ${\displaystyle z\in \mathbb {C} }$ που ικανοποιούν την εξίσωση

${\displaystyle |z-z_{0}|=\rho }$,

όπου ${\displaystyle z_{0}=x_{0}+iy_{0}}$.

Στις κατασκευές με κανόνα και διαβήτη

Η κατασκευή ενός κύκλου με κέντρο δεδομένο σημείο και με δεδομένη ακτίνα, γίνεται με την χρήση ενός διαβήτη. Ο συνδυασμός της χρήσης του χάρακα και του διαβήτη, οδηγεί στην κατασκευή πολλών άλλων γεωμετρικών σχημάτων.

Ένα από τα αρχαιότερα προβλήματα της γεωμετρίας ήταν ο τετραγωνισμός του κύκλου, δηλαδή δοθείσης της ακτίνας ενός κύκλου, να κατασκευαστεί (με κανόνα και διαβήτη) ένα τετράγωνο ίσου εμβαδού με τον κύκλο. Το 1882, ο μαθηματικός Φέρντιναντ Φον Λίντεμαν απέδειξε ότι μία τέτοια κατασκευή είναι αδύνατη.

Στην στερεομετρία

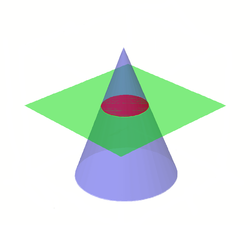
Ο κύκλος προκύπτει ως η τομή ενός κώνου και ενός επιπέδου που είναι κάθετο στον άξονα του κώνου.

Στη γεωμετρία, o τόρος είναι ένα στερεό εκ περιστροφής που προκύπτει από την περιστροφή ενός κύκλου στον τρισδιάστατο χώρο γύρω από έναν άξονα συνεπίπεδο με τον κύκλο, ο οποίος δεν έχει κανένα κοινό σημείο με τον κύκλο.

Η σφαίρα, είναι κατά τον Ευκλείδη το στερεό που προκύπτει από την περιστροφή ενός ημικυκλίου γύρω από την διάμετρό του.^[9] Ισοδύναμα, είναι το σύνολο των σημείων του χώρου που ισαπέχουν από ένα σταθερό σημείο.

Η τομή ενός κώνου και ενός επιπέδου κάθετο στον άξονα του κώνου, δίνει έναν κύκλο.

Ο τόρος προκύπτει ως η περιστροφή ενός κύκλου γύρω από έναν εξωτερικό του άξονα.

Η σφαίρα προκύπτει ως η περιστροφή ενός ημικυκλίου γύρω από μία διάμετρό του.

Γενικεύσεις

Η σφαίρα γενικεύει τον κύκλο ως ο γεωμετρικός τόπος των σημείων που ισαπέχουν από ένα άλλο σημείο στον χώρο τριών διαστάσεων. Η μπάλα είναι ο γεωμετρικός τόπος των σημείων που ισαπέχουν από ένα άλλο σημείο σε έναν γενικό μετρικό χώρο, όπου η απόσταση μπορεί να μην είναι η Ευκλείδεια.

Δείτε επίσης

Commons logo

Τα Wikimedia Commons έχουν πολυμέσα σχετικά με το θέμα    Κύκλος

• Κωνική τομή
• Τετραγωνισμός του κύκλου
• Σφαίρα