Methode der kleinsten Quadrate

Dieser Artikel behandelt die numerischen Aspekte dieser Methode. Für eine stochastische Sichtweise siehe Lineare Einfachregression und Multiple lineare Regression.

Die Methode der kleinsten Quadrate (kurz: MKQ) oder KQ-Methode (englisch method of least squares oder lediglich least squares, kurz: LS); zur Abgrenzung von daraus abgeleiteten Erweiterungen wie z. B. der verallgemeinerten Methode der kleinsten Quadrate oder der zweistufigen Methode der kleinsten Quadrate auch mit dem Zusatz „gewöhnliche“ bezeichnet, d. h. gewöhnliche Methode der kleinsten Quadrate (englisch ordinary least squares, kurz: OLS; veraltet Methode der kleinsten Abweichungsquadratsumme) ist das mathematische Standardverfahren zur Ausgleichungsrechnung.

Dabei wird zu einer Menge von Datenpunkten eine Funktion bestimmt, die möglichst nahe an den Datenpunkten verläuft und somit die Daten bestmöglich zusammenfasst. Die am häufigsten verwendete Funktion ist die Gerade, die dann Ausgleichsgerade genannt wird. Um die Methode anwenden zu können, muss die Funktion mindestens einen Parameter enthalten. Diese Parameter werden dann durch die Methode bestimmt, so dass, wenn die Funktion mit den Datenpunkten verglichen und der Abstand zwischen Funktionswert und Datenpunkt quadriert wird, die Summe dieser quadrierten Abstände möglichst gering wird. Die Abstände werden dann Residuen genannt.

Typischerweise werden mit dieser Methode reale Daten, etwa physikalische oder wirtschaftliche Messwerte, untersucht. Diese Daten beinhalten oft unvermeidbare Messfehler und Schwankungen. Unter der Annahme, dass die gemessenen Werte nahe an den zugrunde liegenden „wahren Werten“ liegen und zwischen den Messwerten ein bestimmter Zusammenhang besteht, kann die Methode verwendet werden, um eine Funktion zu finden, die diesen Zusammenhang der Daten möglichst gut beschreibt. Die Methode kann auch umgekehrt verwendet werden, um verschiedene Funktionen zu testen und dadurch einen unbekannten Zusammenhang in den Daten zu beschreiben.

Messpunkte und deren Abstand von einer nach der Methode der kleinsten Quadrate bestimmten Funktion. Hier wurde eine logistische Funktion als Modellkurve gewählt.

In der Beispielgrafik sind Datenpunkte und eine Ausgleichsfunktion eingetragen. Es wird eine allgemeine Funktion (die Modellfunktion) ausgewählt, die zur Fragestellung und den Daten passen sollte, hier eine logistische Funktion. Deren Parameter werden nun so bestimmt, dass die Summe der Abweichungsquadrate ${\displaystyle e}$ der Beobachtungen ${\displaystyle y}$ von den Werten der Funktion minimiert wird. In der Grafik ist die Abweichung ${\displaystyle e}$ an der Stelle ${\displaystyle x}$ als senkrechter Abstand der Beobachtung ${\displaystyle y}$ von der Kurve zu erkennen.

In der Stochastik wird die Methode der kleinsten Quadrate meistens als regressionsanalytische Schätzmethode benutzt, wo sie auch als Kleinste-Quadrate-Schätzung bzw. gewöhnliche Kleinste-Quadrate-Schätzung bezeichnet wird. Da die Kleinste-Quadrate-Schätzung die Residuenquadratsumme minimiert, ist es dasjenige Schätzverfahren, welches das Bestimmtheitsmaß maximiert. Angewandt als Systemidentifikation ist die Methode der kleinsten Quadrate in Verbindung mit Modellversuchen z. B. für Ingenieure ein Ausweg aus der paradoxen Situation, Modellparameter für unbekannte Gesetzmäßigkeiten zu bestimmen.

Geschichte

Carl Friedrich Gauß

Piazzis Beobachtungen veröffentlicht in der Monatlichen Correspondenz vom September 1801

Am Neujahrstag 1801 entdeckte der italienische Astronom Giuseppe Piazzi den Zwergplaneten Ceres. 40 Tage lang konnte er die Bahn verfolgen, dann verschwand Ceres hinter der Sonne. Im Laufe des Jahres versuchten viele Wissenschaftler erfolglos, anhand von Piazzis Beobachtungen die Bahn zu berechnen – unter der Annahme einer Kreisbahn, denn nur für solche konnten damals die Bahnelemente aus beobachteten Himmelspositionen mathematisch ermittelt werden.

Der 24-jährige Carl Friedrich Gauß schaffte es, die Bahn mit Hilfe einer neuen indirekten Methode der Bahnbestimmung und seiner Ausgleichsrechnungen auf Basis der Methode der kleinsten Quadrate (wenn auch noch nicht so bezeichnet) so zu berechnen, dass Franz Xaver von Zach ihn am 7. Dezember 1801 und – bestätigt – am 31. Dezember 1801 wiederfinden konnte. Heinrich Wilhelm Olbers bestätigte dies unabhängig von Zach durch Beobachtung am 1. und 2. Januar 1802.^[1]

Das Problem der Wiederauffindung der Ceres als solches lag darin, dass durch die Beobachtungen weder der Ort, ein Stück der Bahn, noch die Entfernung bekannt sind, sondern nur die Richtungen der Beobachtung. Dies führt auf die Suche einer Ellipse und nicht nach einem Kreis, wie ihn Gauß’ Konkurrenten ansetzten.^[2] Einer der Brennpunkte der Ellipse ist bekannt (die Sonne selbst), und die Bögen der Bahn der Ceres zwischen den Richtungen der Beobachtung werden nach dem zweiten Keplerschen Gesetz durchlaufen, das heißt, die Zeiten verhalten sich wie die vom Leitstrahl überstrichenen Flächen. Außerdem ist für die rechnerische Lösung bekannt, dass die Beobachtungen selbst von einem Kegelschnitt im Raum ausgehen, der Erdbahn selbst.

Im Grundsatz führt das Problem auf eine Gleichung achten Grades, deren triviale Lösung die Erdbahn selbst ist. Durch umfangreiche Nebenbedingungen und (später) die von Gauß entwickelte Methode der kleinsten Quadrate gelang es dem 24-Jährigen, für die Bahn der Ceres für den 25. November bis 31. Dezember 1801 den von ihm berechneten Ort anzugeben. Damit konnte Zach am letzten Tag der Vorhersage Ceres wiederfinden. Der Ort lag nicht weniger als 7° (d. h. 13,5 Vollmondbreiten) östlich der Stelle, wo die anderen Astronomen Ceres vermutet hatten, was nicht nur Zach, sondern auch Olbers gebührend würdigten.^[3]

Seine ersten Berechnungen waren zwar noch ohne die Methode der kleinsten Quadrate, erst als nach der Wiederentdeckung von Ceres viele neue Daten vorlagen, benutzte er diese für eine genauere Bestimmung der Bahnelemente, ohne aber Details seiner Methode allgemein offenzulegen.^[4] Piazzis Ruf, der aufgrund seiner nicht zu einer Kreisbahn passen wollenden Bahnpunkte stark gelitten hatte, war ebenfalls wiederhergestellt.^[5]

Eine Vorgängermethode der Methode der kleinsten Quadrate stellt die Methode der kleinsten absoluten Abweichungen dar, die 1760 von Rugjer Josip Bošković entwickelt wurde. Die Grundlagen der Methode der kleinsten Quadrate hatte Gauß schon 1795 im Alter von 18 Jahren entwickelt. Zugrundeliegend war eine Idee von Pierre-Simon Laplace, die Abweichungen der Messwerte vom erwarteten Wert so aufzusummieren, dass die Summe über all diese sogenannten Fehler null ergab. Im Unterschied zu dieser Methode verwendete Gauß statt der Fehler die Fehlerquadrate und konnte so auf die Nullsummen-Anforderung verzichten. Unabhängig von Gauß entwickelte der Franzose Adrien-Marie Legendre dieselbe Methode, veröffentlichte diese als Erster im Jahr 1805, am Schluss eines kleinen Werkes über die Berechnung der Kometenbahnen,^[6] und veröffentlichte eine zweite Abhandlung darüber im Jahr 1810. Seine Darstellung war überaus klar und einfach. Von Legendre stammt auch die Bezeichnung Méthode des moindres carrés (Methode der kleinsten Quadrate).

1809 publizierte Gauß dann im zweiten Band seines himmelsmechanischen Werkes Theoria motus corporum coelestium in sectionibus conicis solem ambientium („Theorie der Bewegung der Himmelskörper, welche in Kegelschnitten die Sonne umlaufen“) das Verfahren^[7] inklusive der Normalengleichungen, sowie das Gaußsche Eliminationsverfahren und das Gauß-Newton-Verfahren,^[8] womit er weit über Legendre hinausging. Darin bezeichnete er die Methode der kleinsten Quadrate als seine Entdeckung und behauptete, diese schon im Jahr 1795 (also vor Legendre) entdeckt und angewandt zu haben, was diesen nachhaltig verärgerte. Legendre beschwerte sich darüber in einem langen Brief an Gauß, welchen dieser unbeantwortet ließ.^[9] Gauß verwies nur gelegentlich auf einen Eintrag in seinem mathematischen Tagebuch vom 17. Juni 1798 (dort findet sich der kryptische Satz in Latein: „Calculus probabilitatis contra La Place defensus“ [„Kalkül der Wahrscheinlichkeit gegen Laplace verteidigt“] und sonst nichts).^[10] Laplace beurteilte die Sache so, dass Legendre die Erstveröffentlichung tätigte, Gauß die Methode aber zweifelsfrei schon vorher kannte, selbst nutzte und auch anderen Astronomen brieflich mitteilte.^[11] Die Methode der kleinsten Quadrate wurde nach ihrer Veröffentlichung schnell das Standardverfahren zur Behandlung von astronomischen oder geodätischen Datensätzen.

Gauß nutzte das Verfahren intensiv bei seiner Vermessung des Königreichs Hannover durch Triangulation. 1821 und 1823 erschien die zweiteilige Arbeit sowie 1826 eine Ergänzung zur Theoria combinationis observationum erroribus minimis obnoxiae („Theorie der den kleinsten Fehlern unterworfenen Kombination der Beobachtungen“),^[12] in denen Gauß den Erfolg der Methode der kleinsten Quadrate damit begründete, dass dieses im Vergleich zu anderen Verfahren der Ausgleichungsrechnung in einer breiten Hinsicht optimal ist. Die mathematische Formulierung dieser Aussage ist als Satz von Gauß-Markow bekannt, benannt nach Andrei Andrejewitsch Markow, der diesen anfänglich wenig beachteten Teil der Arbeit Gauß’ im 20. Jahrhundert wiederentdeckt und bekannt gemacht hatte (siehe auch Satz von Gauß-Markow#Geschichte). Die Theoria Combinationis enthält ferner Methoden zum effizienten Lösen linearer Gleichungssysteme, wie das Gauß-Seidel-Verfahren und die LR-Zerlegung, die einen wesentlichen Fortschritt zum damaligen mathematischen Kenntnisstand darstellen.^[13]

Der französische Vermessungsoffizier André-Louis Cholesky entwickelte während des Ersten Weltkriegs die Cholesky-Zerlegung, die gegenüber den Lösungsverfahren von Gauß nochmal einen erheblichen Effizienzgewinn darstellte. In den 1960er Jahren entwickelte Gene Golub die Idee, die auftretenden linearen Gleichungssysteme mittels QR-Zerlegung zu lösen.

Das Verfahren

Voraussetzungen

Man betrachtet eine abhängige Größe ${\displaystyle y}$, die von einer Variablen ${\displaystyle x}$ oder auch von mehreren Variablen beeinflusst wird. So hängt die Dehnung einer Feder nur von der aufgebrachten Kraft ab, die Profitabilität eines Unternehmens jedoch von mehreren Faktoren wie Umsatz, den verschiedenen Kosten oder dem Eigenkapital. Zur Vereinfachung der Notation wird im Folgenden die Darstellung auf eine Variable ${\displaystyle x}$ beschränkt. Der Zusammenhang zwischen ${\displaystyle y}$ und den Variablen wird über eine Modellfunktion ${\displaystyle f}$, beispielsweise eine Parabel oder eine Exponentialfunktion

${\displaystyle y(x)=f(x;\alpha _{1},\dotsc ,\alpha _{m})}$,

die von ${\displaystyle x}$ sowie von ${\displaystyle m}$ Funktionsparametern ${\displaystyle \alpha _{j}}$ abhängt, modelliert. Diese Funktion entstammt entweder der Kenntnis des Anwenders oder einer mehr oder weniger aufwendigen Suche nach einem Modell, eventuell müssen dazu verschiedene Modellfunktionen angesetzt und die Ergebnisse verglichen werden. Ein einfacher Fall auf Basis bereits vorhandener Kenntnis ist beispielsweise die Feder, denn hier ist das Hookesche Gesetz und damit eine lineare Funktion mit der Federkonstanten als einzigem Parameter Modellvoraussetzung. In schwierigeren Fällen wie dem des Unternehmens muss der Wahl des Funktionstyps jedoch ein komplexer Modellierungsprozess vorausgehen.

Um Informationen über die Parameter und damit die konkrete Art des Zusammenhangs zu erhalten, werden zu jeweils ${\displaystyle n}$ gegebenen Werten ${\displaystyle x_{i}}$ der unabhängigen Variablen ${\displaystyle x}$ entsprechende Beobachtungswerte ${\displaystyle y_{i}}$ ${\displaystyle (i=1,\dotsc ,n)}$ erhoben. Die Parameter ${\displaystyle \alpha _{j}}$ dienen zur Anpassung des gewählten Funktionstyps an diese beobachteten Werte ${\displaystyle y_{i}}$. Ziel ist es nun, die Parameter ${\displaystyle \alpha _{j}}$ so zu wählen, dass die Modellfunktion die Daten bestmöglich approximiert.

Gauß und Legendre hatten die Idee, Verteilungsannahmen über die Messfehler dieser Beobachtungswerte zu machen. Sie sollten im Durchschnitt Null sein, eine gleichbleibende Varianz haben und von jedem anderen Messfehler stochastisch unabhängig sein. Man verlangt damit, dass in den Messfehlern keinerlei systematische Information mehr steckt, sie also rein zufällig um Null schwanken. Außerdem sollten die Messfehler normalverteilt sein, was zum einen wahrscheinlichkeitstheoretische Vorteile hat und zum anderen garantiert, dass Ausreißer in ${\displaystyle y}$ so gut wie ausgeschlossen sind.

Um unter diesen Annahmen die Parameter ${\displaystyle \alpha _{j}}$ zu bestimmen, ist es im Allgemeinen notwendig, dass deutlich mehr Datenpunkte als Parameter vorliegen, es muss also ${\displaystyle n>m}$ gelten.

Minimierung der Summe der Fehlerquadrate

Siehe auch: Empirische Risikominimierung

Das Kriterium zur Bestimmung der Approximation sollte so gewählt werden, dass große Abweichungen der Modellfunktion von den Daten stärker gewichtet werden als kleine. Sofern keine Lösung ganz ohne Abweichungen möglich ist, dann ist der Kompromiss mit der insgesamt geringsten Abweichung das beste allgemein gültige Kriterium.

Dazu wird die Summe der Fehlerquadrate, die auch Fehlerquadratsumme (genauer: Residuenquadratsumme) heißt, als die Summe der quadrierten Differenzen zwischen den Werten der Modellkurve ${\displaystyle f(x_{i})}$ und den Daten ${\displaystyle y_{i}}$ definiert.

In Formelschreibweise mit den Parametern ${\displaystyle {\vec {\alpha }}=(\alpha _{1},\alpha _{2},\dots ,\alpha _{m})\in \mathbb {R} ^{m}}$ und ${\displaystyle {\vec {f}}=(f(x_{1},{\vec {\alpha }}),\dots ,f(x_{n},{\vec {\alpha }}))\in \mathbb {R} ^{n}}$ ergibt sich

${\displaystyle \sum _{i=1}^{n}(f(x_{i},{\vec {\alpha }})-y_{i})^{2}=\|{\vec {f}}-{\vec {y}}\|_{2}^{2}.}$

Es sollen dann diejenigen Parameter ${\displaystyle \alpha _{j}}$ ausgewählt werden, bei denen die Summe der quadrierten Anpassungsfehler minimal wird:

${\displaystyle \min _{\vec {\alpha }}\|{\vec {f}}-{\vec {y}}\|_{2}^{2}.}$

Wie genau dieses Minimierungsproblem gelöst wird, hängt von der Art der Modellfunktion ab.

Wird die Fehlerquadratsumme für einen externen Datensatz vorhergesagt, so spricht man von der PRESS-Statistik (englisch predictive residual sum of squares).

Zusammenhang mit dem zentralen Grenzwertsatz

Selbst wenn die Fehlerterme nicht normalverteilt sind, folgt aus dem zentralen Grenzwertsatz oft, dass der Schätzer der bedingten Erwartung ${\displaystyle f(x,\alpha )={\hat {E}}[Y|x]}$ approximativ normalverteilt ist, solange die Stichprobe hinreichend groß ist. Aus diesem Grund ist die Verteilung des Fehlerterms bei großen Stichprobenumfängen oft kein gravierendes Problem in der Regressionsanalyse. Speziell ist es häufig nicht wichtig, ob der Fehlerterm einer Normalverteilung folgt, es sei denn es liegen beispielsweise folgende Punkte vor^[14]:

• die Stichprobengröße ist klein
• die Verteilung der Fehler ist eine Heavy-tailed-Verteilung, welche zur Erzeugung von Daten führt, welche weit weg von den anderen Daten liegen (Stichproben aus den Heavy tails werden dann oft als Ausreißer interpretiert)
• Multimodale Fehlerverteilungen
• große Schiefe der Fehlerverteilung

Lineare Modellfunktion

Lineare Modellfunktionen sind Linearkombinationen aus beliebigen, im Allgemeinen nicht-linearen Basisfunktionen. Für solche Modellfunktionen lässt sich das Minimierungsproblem auch analytisch über einen Extremwertansatz ohne iterative Annäherungsschritte lösen. Zunächst werden einige einfache Spezialfälle und Beispiele gezeigt.

Spezialfall einer einfachen linearen Ausgleichsgeraden

Herleitung und Verfahren

Eine einfache Modellfunktion mit zwei linearen Parametern stellt das Polynom erster Ordnung

${\displaystyle f(x)=\alpha _{0}+\alpha _{1}x}$

dar. Gesucht werden zu ${\displaystyle n}$ gegebenen Messwerten ${\displaystyle (x_{1},y_{1}),\dotsc ,(x_{n},y_{n})}$ die Koeffizienten ${\displaystyle \alpha _{0}}$ und ${\displaystyle \alpha _{1}}$ der bestangepassten Geraden. Die Abweichungen ${\displaystyle r_{i}}$ zwischen der gesuchten Geraden und den jeweiligen Messwerten

${\displaystyle {\begin{matrix}r_{1}=&\alpha _{0}+&\alpha _{1}x_{1}-y_{1}\\r_{2}=&\alpha _{0}+&\alpha _{1}x_{2}-y_{2}\\\vdots &\vdots &\vdots \\r_{n}=&\alpha _{0}+&\alpha _{1}x_{n}-y_{n}\\\end{matrix}}}$

nennt man Anpassungsfehler oder Residuen. Gesucht sind nun die Koeffizienten ${\displaystyle \alpha _{0}}$ und ${\displaystyle \alpha _{1}}$ mit der kleinsten Summe der Fehlerquadrate

${\displaystyle \min _{\alpha _{0},\alpha _{1}}\sum _{i=1}^{n}r_{i}^{2}}$.

Der große Vorteil des Ansatzes mit diesem Quadrat der Fehler wird sichtbar, wenn man diese Minimierung mathematisch durchführt: Die Summenfunktion wird als Funktion der beiden Variablen ${\displaystyle \alpha _{0}}$ und ${\displaystyle \alpha _{1}}$ aufgefasst (die eingehenden Messwerte sind dabei numerische Konstanten), dann die Ableitung (genauer: partielle Ableitungen) der Funktion nach diesen Variablen (also ${\displaystyle \alpha _{0}}$ und ${\displaystyle \alpha _{1}}$) gebildet und von dieser Ableitung schließlich die Nullstelle gesucht. Es ergibt sich das lineare Gleichungssystem

${\displaystyle {\begin{aligned}\textstyle n\cdot \alpha _{0}+\left(\sum \limits _{i=1}^{n}x_{i}\right)\alpha _{1}&=\textstyle \sum \limits _{i=1}^{n}y_{i}\\\textstyle \left(\sum \limits _{i=1}^{n}x_{i}\right)\alpha _{0}+\left(\sum \limits _{i=1}^{n}x_{i}^{2}\right)\alpha _{1}&=\textstyle \sum \limits _{i=1}^{n}x_{i}y_{i}\end{aligned}}}$

mit der Lösung

${\displaystyle \alpha _{1}={\frac {\sum \nolimits _{i=1}^{n}x_{i}(y_{i}-{\overline {y}})}{\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}={\frac {\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}{\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}={\frac {SP_{xy}}{SQ_{x}}}}$ und ${\displaystyle \;\alpha _{0}={\overline {y}}-\alpha _{1}{\overline {x}}}$,

wobei ${\displaystyle SP_{xy}}$ die Summe der Abweichungsprodukte zwischen ${\displaystyle x}$ und ${\displaystyle y}$ darstellt, und ${\displaystyle SQ_{x}}$ die Summe der Abweichungsquadrate von ${\displaystyle x}$ darstellt. Dabei ist ${\displaystyle \textstyle {\overline {x}}={\frac {1}{n}}\sum \nolimits _{i=1}^{n}x_{i}}$ das arithmetische Mittel der ${\displaystyle x}$-Werte, ${\displaystyle {\overline {y}}}$ entsprechend. Die Lösung für ${\displaystyle \alpha _{1}}$ kann mit Hilfe des Verschiebungssatzes auch in nicht-zentrierter Form

${\displaystyle \alpha _{1}={\frac {\sum _{i=1}^{n}(x_{i}y_{i})-n{\overline {x}}{\overline {y}}}{\left(\sum _{i=1}^{n}x_{i}^{2}\right)-n{\overline {x}}^{2}}}}$

angegeben werden. Diese Ergebnisse können auch mit Funktionen einer reellen Variablen, also ohne partielle Ableitungen, hergeleitet werden.^[15]

Aus der Lösung von ${\displaystyle \alpha _{0}}$ wird zudem eine Eigenschaft der linearen Ausgleichsgerade ersichtlich: Die Ausgleichsgerade verläuft stets durch den Punkt ${\displaystyle ({\overline {x}},{\overline {y}})}$. Das ist hilfreich, falls die Ausgleichsgerade sehr steil oder gar senkrecht verläuft und der Achsenabschnitt dadurch sehr groß wird oder gar nicht berechnet werden kann. In diesem Fall kann dieser Punkt als Stützpunkt einer Vektordarstellung der Ausgleichsgerade verwendet werden.

Beispiel mit einer Ausgleichsgeraden

In diesem Beispiel wird eine Ausgleichsgerade der Form ${\displaystyle f(x)=\alpha _{0}+\alpha _{1}x}$ berechnet, um den Zusammenhang zwischen zwei Merkmalen eines Datensatzes darzustellen. Der Datensatz besteht aus Länge und Breite von zehn Kriegsschiffen (siehe Kriegsschiffsdaten). Es soll versucht werden, die Breite mit der Länge in Bezug zu setzen. Die Daten werden in der folgenden Tabelle in den ersten drei Spalten wiedergegeben. Die weiteren Spalten beziehen sich auf Zwischenergebnisse zur Berechnung der Ausgleichsgeraden. Die Variable ${\displaystyle x_{i}}$ soll dabei die Länge des Kriegsschiffs ${\displaystyle i}$ bezeichnen und ${\displaystyle y_{i}}$ dessen Breite. Gesucht ist die Gerade ${\displaystyle f(x)=y=\alpha _{0}+\alpha _{1}x}$ für die, wenn die bekannten Werte ${\displaystyle x_{i}}$ eingesetzt werden, die Funktionswerte ${\displaystyle f(x_{i})={\tilde {y}}_{i}}$ möglichst nahe an den bekannten Werten ${\displaystyle y_{i}}$ liegen.

Kriegsschiff	Länge (m)	Breite (m)	${\displaystyle (x_{i}-{\overline {x}})}$	${\displaystyle (y_{i}-{\overline {y}})}$
${\displaystyle i}$	${\displaystyle x_{i}}$	${\displaystyle y_{i}}$	${\displaystyle x_{i}^{*}}$	${\displaystyle y_{i}^{*}}$	${\displaystyle x_{i}^{*}\cdot y_{i}^{*}}$	${\displaystyle (x_{i}^{*})^{2}}$	${\displaystyle f(x_{i})}$	${\displaystyle f(x_{i})-y_{i}}$
1	208	21,6	40,2	3,19	128,24	1616,04	24,88	3,28
2	152	15,5	−15,8	−2,91	45,98	249,64	15,86	0,36
3	113	10,4	−54,8	−8,01	438,95	3003,04	9,57	−0,83
4	227	31,0	59,2	12,59	745,33	3504,64	27,95	−3,05
5	137	13,0	−30,8	−5,41	166,63	948,64	13,44	0,44
6	238	32,4	70,2	13,99	982,10	4928,04	29,72	−2,68
7	178	19,0	10,2	0,59	6,02	104,04	20,05	1,05
8	104	10,4	−63,8	−8,01	511,04	4070,44	8,12	−2,28
9	191	19,0	23,2	0,59	13,69	538,24	22,14	3,14
10	130	11,8	−37,8	−6,61	249,86	1428,84	12,31	0,51
Summe Σ	1678	184,1			3287,82	20391,60

Die Ausgleichsgerade wird durch die Koeffizienten ${\displaystyle \alpha _{0}}$ und ${\displaystyle \alpha _{1}}$ bestimmt, die wie oben angegeben berechnet werden mit

${\displaystyle \alpha _{1}={\frac {\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})}{\sum \nolimits _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}={\frac {SP_{xy}}{SQ_{x}}}}$

${\displaystyle \alpha _{0}={\overline {y}}-\alpha _{1}{\overline {x}}}$

Die Konstanten ${\displaystyle {\overline {x}}}$ und ${\displaystyle {\overline {y}}}$ sind jeweils die Mittelwerte der ${\displaystyle x}$- und ${\displaystyle y}$-Messwerte, also

${\displaystyle {\overline {x}}={\frac {\sum \nolimits _{i=1}^{n}x_{i}}{n}}={\frac {1678}{10}}=167{,}8}$

${\displaystyle {\overline {y}}={\frac {184,1}{10}}=18{,}41}$

Als erster Zwischenschritt kann nun für jedes Kriegsschiff die Abweichung vom Mittelwert berechnet werden: ${\displaystyle x_{i}^{*}=(x_{i}-{\overline {x}})}$ und ${\displaystyle \;y_{i}^{*}=(y_{i}-{\overline {y}})}$ – diese Werte sind in der vierten und fünften Spalte der oberen Tabelle eingetragen. Die Formel für ${\displaystyle \alpha _{1}}$ vereinfacht sich dadurch zu

${\displaystyle \alpha _{1}={\frac {\sum \nolimits _{i=1}^{n}x_{i}^{*}\cdot y_{i}^{*}}{\sum \nolimits _{i=1}^{n}(x_{i}^{*})^{2}}}}$

Als zweiter Zwischenschritt können die Produkte ${\displaystyle x_{i}^{*}\cdot y_{i}^{*}}$ und ${\displaystyle (x_{i}^{*})^{2}}$ für jedes Kriegsschiff berechnet werden. Diese Werte sind in der sechsten und siebten Spalte der Tabelle eingetragen und lassen sich nun einfach aufsummieren. Damit kann ${\displaystyle \alpha _{1}}$ berechnet werden als

${\displaystyle \alpha _{1}={\frac {3287{,}82}{20391{,}60}}=0{,}1612}$

Der Wert von ${\displaystyle \alpha _{1}}$ kann bereits interpretiert werden: Mit der Annahme, dass die Daten in einem linearen Zusammenhang stehen und durch unsere berechnete Ausgleichsgerade beschrieben werden können, steigt die Breite eines Kriegsschiffes um ca. 0,16 Meter für jeden ganzen Meter, um den es länger ist.

Der Achsenabschnitt ${\displaystyle \alpha _{0}}$ ist dann

${\displaystyle \alpha _{0}={\overline {y}}-\alpha _{1}{\overline {x}}=18{,}41-0{,}1612\cdot 167{,}8=-8{,}6451}$

Streudiagramm von Längen und Breiten von zehn zufällig ausgewählten Kriegsschiffen mit eingezeichneter linearer Ausgleichsfunktion

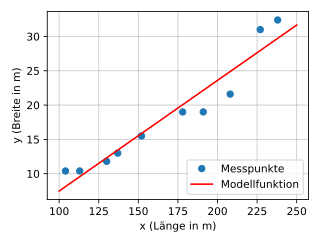
Die Gleichung der Ausgleichsgerade lautet somit ${\displaystyle f(x)=-8{,}6451+0{,}1612x}$

Zur Veranschaulichung können die Daten als Streudiagramm aufgezeichnet und die Ausgleichsgerade eingefügt werden. Das Diagramm legt nahe, dass für unsere Beispieldaten zwischen Länge und Breite eines Kriegsschiffs tatsächlich ein linearer Zusammenhang besteht. Die Anpassung der Punkte ist recht gut. Als Maß kann auch die Abweichung ${\displaystyle f(x_{i})-y_{i}}$ der durch die Gerade vorhergesagten Werte ${\displaystyle f(x_{i})}$ von den gemessenen Werten ${\displaystyle y_{i}}$ betrachtet werden. Die entsprechenden Werte sind in der achten und neunten Spalte der Tabelle eingetragen. Die Abweichung beträgt im Mittel 2,1 m. Auch das Bestimmtheitsmaß, als normierter Koeffizient, ergibt einen Wert von ca. 92,2 % (100 % würde einer mittleren Abweichung von 0 m entsprechen); zur Berechnung siehe das Beispiel zum Bestimmtheitsmaß.

Allerdings bedeutet der negative Achsenabschnitt ${\displaystyle \alpha _{0}}$, dass in unserem linearen Modell ein Kriegsschiff mit einer Länge von 0 Metern eine negative Breite besitzt – oder Kriegsschiffe erst ab einer gewissen Mindestlänge zu existieren beginnen. Verglichen mit der Realität ist das natürlich falsch, was bei der Beurteilung einer statistischen Analyse berücksichtigt werden kann. Wahrscheinlich ist, dass das Modell nur für den Bereich gültig ist, für den tatsächlich Messwerte vorliegen (in diesem Fall für Kriegsschiffslängen zwischen 100 m und 240 m) und außerhalb des Bereiches eine lineare Funktion nicht mehr geeignet ist, um die Daten darzustellen.

Einfache polynomiale Ausgleichskurven

Streudiagramm: Durchschnittliches Gewicht von Männern nach Alter mit parabelförmiger Modellfunktion

Datensatz mit approximierenden Polynomen

Allgemeiner als eine lineare Ausgleichsgerade sind Ausgleichspolynome

${\displaystyle y(x)\approx \alpha _{0}+\alpha _{1}x+\alpha _{2}x^{2}+\dotsb +\alpha _{q}x^{q}}$,

die nun anhand eines Beispiels illustriert werden (auch solche Ausgleichspolynomansätze lassen sich – zusätzlich zur iterativen Lösung – analytisch über einen Extremwertansatz lösen).

Als Ergebnisse der Mikrozensus-Befragung durch das statistische Bundesamt sind die durchschnittlichen Gewichte von Männern nach Altersklassen gegeben (Quelle: Statistisches Bundesamt, Wiesbaden 2009). Für die Analyse wurden die Altersklassen durch die Klassenmitten ersetzt. Es soll die Abhängigkeit der Variablen Gewicht (${\displaystyle y}$) von der Variablen Alter (${\displaystyle x}$) analysiert werden.

Das Streudiagramm lässt auf eine annähernd parabolische Beziehung zwischen ${\displaystyle x}$ und ${\displaystyle y}$ schließen, welche sich häufig gut durch ein Polynom annähern lässt. Es wird ein polynomialer Ansatz der Form

${\displaystyle y(x)\approx \alpha _{0}+\alpha _{1}x+\alpha _{2}x^{2}+\alpha _{3}x^{3}+\alpha _{4}x^{4}}$

versucht. Als Lösung ergibt sich das Polynom 4. Grades

${\displaystyle y(x)\approx 47{,}86+2{,}2x-0{,}04809x^{2}+0{,}0004935x^{3}-0{,}000002148x^{4}}$.

Die Messpunkte weichen im Mittel (Standardabweichung) 0,19 kg von der Modellfunktion ab. Reduziert man den Grad des Polynoms auf 3, erhält man die Lösung

${\displaystyle y(x)\approx 54{,}22+1{,}515x-0{,}0226x^{2}+0{,}0001002x^{3}}$

mit einer mittleren Abweichung von 0,22 kg und beim Polynomgrad 2 die Lösung

${\displaystyle y(x)\approx 61{,}42+0{,}9397x-0{,}008881x^{2}}$

mit einer mittleren Abweichung von 0,42 kg. Wie zu erkennen ist, ändern sich beim Wegfallen der höheren Terme die Koeffizienten der niedrigeren Terme. Die Methode versucht, das Beste aus jeder Situation herauszuholen. Entsprechend werden die fehlenden höheren Terme mit Hilfe der niedrigeren Terme so gut wie möglich ausgeglichen, bis das mathematische Optimum erreicht ist. Mit dem Polynom zweiten Grades (Parabel) wird der Verlauf der Messpunkte noch sehr gut beschrieben (siehe Abbildung).

Spezialfall einer linearen Ausgleichsfunktion mit mehreren Variablen

Ist die Modellfunktion ein mehrdimensionales Polynom erster Ordnung, besitzt also statt nur einer Variablen ${\displaystyle x}$ mehrere unabhängige Modellvariablen ${\displaystyle x_{1},\ldots ,x_{N}}$, erhält man eine lineare Funktion der Form

${\displaystyle f(x_{1},\dotsc ,x_{N};\alpha _{0},\alpha _{1},\dotsc ,\alpha _{N})=\alpha _{0}+\alpha _{1}x_{1}+\dotsb +\alpha _{N}x_{N}}$,

die auf die Residuen

${\displaystyle {\begin{matrix}r_{1}=&\alpha _{0}+\alpha _{1}x_{1,1}+&\dotsb \;\;+\alpha _{j}x_{j,1}+&\dotsb \;\;+\alpha _{N}x_{N,1}-y_{1}\\r_{2}=&\alpha _{0}+\alpha _{1}x_{1,2}+&\dotsb \;\;+\alpha _{j}x_{j,2}+&\dotsb \;\;+\alpha _{N}x_{N,2}-y_{2}\\\vdots &\vdots &\vdots &\vdots \\r_{i}=&\alpha _{0}+\alpha _{1}x_{1,i}+&\dotsb \;\;+\alpha _{j}x_{j,i}+&\dotsb \;\;+\alpha _{N}x_{N,i}-y_{i}\\\vdots &\vdots &\vdots &\vdots \\r_{n}=&\alpha _{0}+\alpha _{1}x_{1,n}+&\dotsb \;\;+\alpha _{j}x_{j,n}+&\dotsb \;\;+\alpha _{N}x_{N,n}-y_{n}\\\end{matrix}}}$

führt und über den Minimierungsansatz

${\displaystyle \min _{\alpha }\sum _{i=1}^{n}r_{i}^{2}}$

gelöst werden kann.

Der allgemeine lineare Fall

Zweidimensionale Polynomfläche zweiter Ordnung mit 3 × 3 = 9 Basisfunktionen:
f(x₁, x₂) = ${\displaystyle \alpha }$₀ + ${\displaystyle \alpha }$₁x₁¹ + ${\displaystyle \alpha }$₂x₁² + ${\displaystyle \alpha }$₃x₂¹ + ${\displaystyle \alpha }$₄x₁¹x₂¹ + ${\displaystyle \alpha }$₅x₁²x₂¹ + ${\displaystyle \alpha }$₆x₂² + ${\displaystyle \alpha }$₇x₁¹x₂² + ${\displaystyle \alpha }$₈x₁²x₂²

Im Folgenden soll der allgemeine Fall von beliebigen linearen Modellfunktionen mit beliebiger Dimension gezeigt werden. Zu einer gegebenen Messwertfunktion

${\displaystyle y(x_{1},x_{2},\dots ,x_{N})}$

mit ${\displaystyle N}$ unabhängigen Variablen sei eine optimal angepasste lineare Modellfunktion

${\displaystyle f(x_{1},x_{2},\dots ,x_{N};\alpha _{1},\alpha _{2},\dots ,\alpha _{m})=\sum _{j=1}^{m}\alpha _{j}\varphi _{j}(x_{1},x_{2},\dots ,x_{N})}$

gesucht, deren quadratische Abweichung dazu minimal sein soll. ${\displaystyle x_{i}}$ sind dabei die Funktionskoordinaten, ${\displaystyle \alpha _{j}}$ die zu bestimmenden linear eingehenden Parameter und ${\displaystyle \varphi _{j}}$ beliebige zur Anpassung an das Problem gewählte linear unabhängige Funktionen.

Bei ${\displaystyle n}$ gegebenen Messpunkten

${\displaystyle (x_{1,1},x_{2,1},\dots ,x_{N,1};y_{1}),(x_{1,2},x_{2,2},\dots ,x_{N,2};y_{2}),\dots ,(x_{1,n},x_{2,n},\dots ,x_{N,n};y_{n})}$

erhält man die Anpassungsfehler

${\displaystyle {\begin{matrix}r_{1}=&\alpha _{1}\varphi _{1}(x_{1,1},\dots ,x_{N,1})\;\;+&\alpha _{2}\varphi _{2}(x_{1,1},\dots ,x_{N,1})+&\cdots \;\;\;+\alpha _{m}\varphi _{m}(x_{1,1},\dots ,x_{N,1})-y_{1}\\r_{2}=&\alpha _{1}\varphi _{1}(x_{1,2},\dots ,x_{N,2})\;\;+&\alpha _{2}\varphi _{2}(x_{1,2},\dots ,x_{N,2})+&\cdots \;\;\;+\alpha _{m}\varphi _{m}(x_{1,2},\dots ,x_{N,2})-y_{2}\\\vdots &\vdots &\vdots &\vdots \\r_{i}=&\alpha _{1}\varphi _{1}(x_{1,i},\dots ,x_{N,i})\;\;+&\alpha _{2}\varphi _{2}(x_{1,i},\dots ,x_{N,i})+&\cdots \;\;\;+\alpha _{m}\varphi _{m}(x_{1,i},\dots ,x_{N,i})-y_{i}\\\vdots &\vdots &\vdots &\vdots \\r_{n}=&\alpha _{1}\varphi _{1}(x_{1,n},\dots ,x_{N,n})\;\;+&\alpha _{2}\varphi _{2}(x_{1,n},\dots ,x_{N,n})+&\cdots \;\;\;+\alpha _{m}\varphi _{m}(x_{1,n},\dots ,x_{N,n})-y_{n}\\\end{matrix}}}$

oder in Matrixschreibweise

${\displaystyle r=A\alpha -y,}$

wobei der Vektor ${\displaystyle r\in \mathbb {R} ^{n}}$ die ${\displaystyle r_{i}}$ zusammenfasst, die Matrix ${\displaystyle A\in \mathbb {R} ^{n\times m}}$ die Basisfunktionswerte ${\displaystyle A_{ij}:=\varphi _{j}(x_{1,i},\dots ,x_{N,i})}$, der Parametervektor ${\displaystyle \alpha \in \mathbb {R} ^{m}}$ die Parameter ${\displaystyle \alpha _{j}}$ und der Vektor ${\displaystyle y\in \mathbb {R} ^{n}}$ die Beobachtungen ${\displaystyle y_{i}}$, wo ${\displaystyle n\geq m}$.

Der beste Schätzer wird durch die Lösung des Minimierungsproblems bestimmt. Das Minimierungsproblem, das sich mithilfe der euklidischen Norm durch

${\displaystyle \min _{\alpha }\sum _{i=1}^{n}r_{i}^{2}=\min _{\alpha }\|f(\alpha )-y\|_{2}^{2}=\min _{\alpha }\|A\alpha -y\|_{2}^{2}}$

formulieren lässt, kann im regulären Fall (d. h. ${\displaystyle A}$ hat vollen Spaltenrang, somit ist ${\displaystyle A^{T}A}$ regulär und damit invertierbar) mit der Formel

${\displaystyle {\hat {\alpha }}=(A^{T}A)^{-1}A^{T}y}$

eindeutig analytisch gelöst werden (siehe nächster Abschnitt). Im generalisierten Fall der gewichteten kleinsten Quadrate muss zudem noch die inverse Kovarianzmatrix ${\displaystyle V^{-1}}$ berücksichtigt werden

${\displaystyle {\hat {\alpha }}=(A^{T}V^{-1}A)^{-1}A^{T}V^{-1}y.}$

Im singulären Fall, wenn ${\displaystyle A}$ nicht von vollem Rang ist, ist das Normalgleichungssystem nicht eindeutig lösbar, d. h. der Parameter ${\displaystyle \alpha }$ nicht identifizierbar (siehe Satz von Gauß-Markow#Singulärer Fall, schätzbare Funktionen).

Jedoch ist in vielen praktischen Anwendungen die Modellfunktionen ${\displaystyle y(x_{1},x_{2},\dots ,x_{N})}$ nicht analytisch bekannt, sondern kann nur für verschiedene diskrete Werte ${\displaystyle (x_{1},x_{2},\dots ,x_{N})}$ bestimmt werden. In diesem Fall kann die Modellfunktion mithilfe einer linearen Regression näherungsweise bestimmt werden, und der beste Schätzer wird direkt mit der Gleichung des linearen Template Fits^[16] bestimmt:

${\displaystyle {\hat {\alpha }}=\left((Y{\tilde {M}})^{\mathsf {T}}V^{-1}Y{\tilde {M}}\right)^{-1}(Y{\tilde {M}})^{\mathsf {T}}V^{-1}(d-Y{\bar {m}}).}$

Dabei ist ${\displaystyle \mathbf {Y} }$ die Matrix mit den bekannten Werten der Modellfunktion (Template Matrix) für alle ${\displaystyle {\boldsymbol {x}}}$, und der Vektor ${\displaystyle \mathbf {d} }$ bezeichnet die Zufallsvariablen (bspw. eine Messung). Die Matrix ${\displaystyle \mathbf {\tilde {M}} }$ und der Vektor ${\displaystyle \mathbf {\tilde {m}} }$ werden mithilfe der Stützstellen ${\displaystyle \mathbf {x} }$ (zusammengefasst in der Matrix ${\displaystyle Y}$) berechnet.

Lösung des Minimierungsproblems

Herleitung und Verfahren

Das Minimierungsproblem ergibt sich, wie im allgemeinen linearen Fall gezeigt, als

${\displaystyle \min _{\alpha }\|A\alpha -y\|_{2}^{2}=\min _{\alpha }(A\alpha -y)^{T}(A\alpha -y)=\min _{\alpha }(\alpha ^{T}A^{T}A\alpha -2y^{T}A\alpha +y^{T}y).}$

Dieses Problem ist immer lösbar. Hat die Matrix ${\displaystyle A}$ vollen Rang, so ist die Lösung sogar eindeutig. Zum Bestimmen des extremalen Punktes ergibt Nullsetzen der partiellen Ableitungen bezüglich der ${\displaystyle \alpha _{j}}$,

${\displaystyle \nabla \|A\alpha -y\|_{2}^{2}=2(A\alpha -y)^{T}A,}$

ein lineares System von Normalgleichungen (auch Gaußsche Normalgleichungen oder Normalengleichungen)

${\displaystyle A^{T}A\alpha =A^{T}y,}$

welches die Lösung des Minimierungsproblems liefert und im Allgemeinen numerisch gelöst werden muss. Hat ${\displaystyle A}$ vollen Rang und ist ${\displaystyle n\geq m}$, so ist die Matrix ${\displaystyle A^{T}A}$ positiv definit, so dass es sich beim gefundenen Extremum in der Tat um ein Minimum handelt.^[17] Damit kann das Lösen des Minimierungsproblems auf das Lösen eines Gleichungssystems reduziert werden. Im einfachen Fall einer Ausgleichsgeraden kann dessen Lösung, wie gezeigt wurde, sogar direkt als einfache Formel angegeben werden.

Alternativ lassen sich die Normalgleichungen in der Darstellung

${\displaystyle A^{T}A\alpha -A^{T}y={\begin{pmatrix}\left\langle \varphi _{1},\varphi _{1}\right\rangle &\left\langle \varphi _{1},\varphi _{2}\right\rangle &\cdots &\left\langle \varphi _{1},\varphi _{m}\right\rangle \\\left\langle \varphi _{2},\varphi _{1}\right\rangle &\left\langle \varphi _{2},\varphi _{2}\right\rangle &\cdots &\left\langle \varphi _{2},\varphi _{m}\right\rangle \\\vdots &\vdots &\ddots &\vdots \\\left\langle \varphi _{m},\varphi _{1}\right\rangle &\left\langle \varphi _{m},\varphi _{2}\right\rangle &\cdots &\left\langle \varphi _{m},\varphi _{m}\right\rangle \\\end{pmatrix}}{\begin{pmatrix}\alpha _{1}\\\alpha _{2}\\\vdots \\\alpha _{m}\end{pmatrix}}-{\begin{pmatrix}\left\langle y,\varphi _{1}\right\rangle \\\left\langle y,\varphi _{2}\right\rangle \\\vdots \\\left\langle y,\varphi _{m}\right\rangle \\\end{pmatrix}}=0.}$

ausschreiben, wobei ${\displaystyle \left\langle \cdot ,\cdot \right\rangle }$ das Standardskalarprodukt symbolisiert und auch als Integral des Überlapps der Basisfunktionen verstanden werden kann. Die Basisfunktionen ${\displaystyle \varphi _{i}}$ sind als Vektoren ${\displaystyle {\vec {\varphi _{i}}}=(\varphi _{i}(x_{1,1},\dots ,x_{N,1}),\varphi _{i}(x_{1,2},\dots ,x_{N,2}),\ldots ,\varphi _{i}(x_{1,n},\dots ,x_{N,n}))}$ zu lesen mit den ${\displaystyle n}$ diskreten Stützstellen am Ort der Beobachtungen ${\displaystyle y={\vec {y}}=(y_{1},y_{2},\ldots ,y_{n})}$.

Ferner lässt sich das Minimierungsproblem mit einer Singulärwertzerlegung gut analysieren. Diese motivierte auch den Ausdruck der Pseudoinversen, einer Verallgemeinerung der normalen Inversen einer Matrix. Diese liefert dann eine Sichtweise auf nichtquadratische lineare Gleichungssysteme, die einen nicht stochastisch, sondern algebraisch motivierten Lösungsbegriff erlaubt.

Numerische Behandlung der Lösung

Zur numerischen Lösung des Problems gibt es zwei Wege. Zum einen können die Normalgleichungen

${\displaystyle A^{T}A\alpha =A^{T}y}$

gelöst werden, die eindeutig lösbar sind, falls die Matrix ${\displaystyle A}$ vollen Rang hat. Ferner hat die Produktsummenmatrix ${\displaystyle A^{T}A}$ die Eigenschaft, positiv definit zu sein, ihre Eigenwerte sind also alle positiv. Zusammen mit der Symmetrie von ${\displaystyle A^{T}A}$ kann dies beim Einsatz von numerischen Verfahren zur Lösung ausgenutzt werden: beispielsweise mit der Cholesky-Zerlegung oder dem CG-Verfahren. Da beide Methoden von der Kondition der Matrix stark beeinflusst werden, ist dies manchmal keine empfehlenswerte Herangehensweise: Ist schon ${\displaystyle A}$ schlecht konditioniert, so ist ${\displaystyle A^{T}A}$ quadratisch schlecht konditioniert. Dies führt dazu, dass Rundungsfehler so weit verstärkt werden können, dass sie das Ergebnis unbrauchbar machen. Durch Regularisierungsmethoden kann die Kondition allerdings verbessert werden.

Eine Methode ist die sog. Ridge-Regression, die auf Hoerl und Kennard (1970) zurückgeht.^[18] Das englische Wort ridge heißt so viel wie Grat, Riff, Rücken. Hier wird anstelle der schlecht konditionierten Matrix ${\displaystyle A^{T}A}$ die besser konditionierte Matrix ${\displaystyle A^{T}A+\delta I_{m}}$ benutzt. Dabei ist ${\displaystyle I_{m}}$ die ${\displaystyle m}$-dimensionale Einheitsmatrix. Die Kunst besteht in der geeigneten Wahl von ${\displaystyle \delta }$. Zu kleine ${\displaystyle \delta }$ erhöhen die Kondition nur wenig, zu große ${\displaystyle \delta }$ führen zu verzerrter Anpassung.

Zum anderen liefert das ursprüngliche Minimierungsproblem eine stabilere Alternative, da es bei kleinem Wert des Minimums eine Kondition in der Größenordnung der Kondition von ${\displaystyle A}$, bei großen Werten des Quadrats der Kondition von ${\displaystyle A}$ hat. Um die Lösung zu berechnen, wird eine QR-Zerlegung verwendet, die mit Householdertransformationen oder Givens-Rotationen erzeugt wird. Grundidee ist, dass orthogonale Transformationen die euklidische Norm eines Vektors nicht verändern. Damit ist

${\displaystyle \|A\alpha -y\|_{2}=\|Q(A\alpha -y)\|_{2}}$

für jede orthogonale Matrix ${\displaystyle Q}$. Zur Lösung des Problems kann also eine QR-Zerlegung von ${\displaystyle A}$ berechnet werden, wobei man die rechte Seite direkt mittransformiert. Dies führt auf eine Form

${\displaystyle \|R\alpha -Q^{T}y\|_{2}}$

mit ${\displaystyle R={\begin{pmatrix}{\tilde {R}}\\0\end{pmatrix}},}$ wobei ${\displaystyle {\tilde {R}}\in \mathbb {R} ^{m\times m}}$ eine rechte obere Dreiecksmatrix ist. Die Lösung des Problems ergibt sich somit durch die Lösung des Gleichungssystems

${\displaystyle {\tilde {R}}{\begin{pmatrix}\alpha _{1}\\\vdots \\\alpha _{m}\end{pmatrix}}={\begin{pmatrix}(Q^{T}y)_{1}\\\vdots \\(Q^{T}y)_{m}\end{pmatrix}}.}$

Die Norm des Minimums ergibt sich dann aus den restlichen Komponenten der transformierten rechten Seite ${\displaystyle (Qy)_{m+1},\dots ,(Qy)_{n},}$ da die dazugehörigen Gleichungen aufgrund der Nullzeilen in ${\displaystyle R}$ nie erfüllt werden können.

In der statistischen Regressionsanalyse spricht man bei mehreren gegebenen Variablen ${\displaystyle x_{1},\ldots ,x_{n}}$ von multipler linearer Regression. Der gebräuchlichste Ansatz ein multiples lineares Modell zu schätzen ist als die gewöhnliche Kleinste-Quadrate-Schätzung bzw. gewöhnliche Methode der kleinsten Quadrate (englisch ordinary least squares, kurz OLS) bekannt. Im Gegensatz zur gewöhnlichen KQ-Methode wird die verallgemeinerte Methode der kleinsten Quadrate, kurz VMKQ (englisch generalised least squares, kurz GLS) bei einem verallgemeinerten linearen Regressionsmodell verwendet. Bei diesem Modell weichen die Fehlerterme von der Verteilungsannahme wie Unkorreliertheit und/oder Homoskedastizität ab. Dagegen liegen bei multivariater Regression für jede Beobachtung ${\displaystyle i}$ ${\displaystyle (i=1,\dots ,n)}$ ${\displaystyle r}$ viele ${\displaystyle y}$-Werte vor, so dass statt eines Vektors eine ${\displaystyle n\times r}$-Matrix ${\displaystyle Y}$ vorliegt (siehe Allgemeines lineares Modell). Die linearen Regressionsmodelle sind in der Statistik wahrscheinlichkeitstheoretisch intensiv erforscht worden. Besonders in der Ökonometrie werden beispielsweise komplexe rekursiv definierte lineare Strukturgleichungen analysiert, um volkswirtschaftliche Systeme zu modellieren.

Probleme mit Nebenbedingungen

Häufig sind Zusatzinformationen an die Parameter bekannt, die durch Nebenbedingungen formuliert werden, die dann in Gleichungs- oder Ungleichungsform vorliegen. Gleichungen tauchen beispielsweise auf, wenn bestimmte Datenpunkte interpoliert werden sollen. Ungleichungen tauchen häufiger auf, in der Regel in der Form von Intervallen für einzelne Parameter. Im Einführungsbeispiel wurde die Federkonstante erwähnt, diese ist immer größer Null und kann für den konkret betrachteten Fall immer nach oben abgeschätzt werden.

Im Gleichungsfall können diese bei einem sinnvoll gestellten Problem genutzt werden, um das ursprüngliche Minimierungsproblem in eines einer niedrigeren Dimension umzuformen, dessen Lösung die Nebenbedingungen automatisch erfüllt.

Schwieriger ist der Ungleichungsfall. Hier ergibt sich bei linearen Ungleichungen das Problem

${\displaystyle \min _{\alpha }\|{\vec {f}}-{\vec {y}}\|_{2}\;}$ mit ${\displaystyle \;l\leq C\alpha \leq u}$, ${\displaystyle C\in \mathbb {R} ^{n\times n},}$

wobei die Ungleichungen komponentenweise gemeint sind. Dieses Problem ist als konvexes und quadratisches Optimierungsproblem eindeutig lösbar und kann beispielsweise mit Methoden zur Lösung solcher angegangen werden.

Quadratische Ungleichungen ergeben sich beispielsweise bei der Nutzung einer Tychonow-Regularisierung zur Lösung von Integralgleichungen. Die Lösbarkeit ist hier nicht immer gegeben. Die numerische Lösung kann beispielsweise mit speziellen QR-Zerlegungen erfolgen.

Nichtlineare Modellfunktionen

Grundgedanke und Verfahren

Mit dem Aufkommen leistungsfähiger Rechner gewinnt insbesondere die nichtlineare Regression an Bedeutung. Hierbei gehen die Parameter nichtlinear in die Funktion ein. Nichtlineare Modellierung ermöglicht im Prinzip die Anpassung von Daten an jede Gleichung der Form ${\displaystyle y=f(\alpha )}$. Da diese Gleichungen Kurven definieren, werden die Begriffe nichtlineare Regression und „curve fitting“ zumeist synonym gebraucht.

Manche nichtlineare Probleme lassen sich durch geeignete Substitution in lineare überführen und sich dann wie oben lösen. Ein multiplikatives Modell von der Form

${\displaystyle y=\alpha _{0}\cdot x^{\alpha _{1}}}$

lässt sich beispielsweise durch Logarithmieren in ein additives System überführen. Dieser Ansatz findet unter anderem in der Wachstumstheorie Anwendung.

Im Allgemeinen ergibt sich bei nichtlinearen Modellfunktionen ein Problem der Form

${\displaystyle \min _{\alpha }\|f(\alpha )-y\|_{2},}$

mit einer nichtlinearen Funktion ${\displaystyle f}$. Partielle Differentiation ergibt dann ein System von Normalgleichungen, das nicht mehr analytisch gelöst werden kann. Eine numerische Lösung kann hier iterativ mit dem Gauß-Newton-Verfahren erfolgen.

Aktuelle Programme arbeiten häufig mit einer Variante, dem Levenberg-Marquardt-Algorithmus. Dabei wird durch eine Regularisierung die Monotonie der Näherungsfolge garantiert. Zudem ist das Verfahren bei größerer Abweichung der Schätzwerte toleranter als die Ursprungsmethode. Beide Verfahren sind mit dem Newton-Verfahren verwandt und konvergieren unter geeigneten Voraussetzungen (der Startpunkt ist genügend nahe beim lokalen Optimum) meist quadratisch, in jedem Schritt verdoppelt sich also die Zahl der korrekten Nachkommastellen.

Wenn die Differentiation auf Grund der Komplexität der Zielfunktion zu aufwendig ist, stehen eine Reihe anderer Verfahren als Ausweichlösung zur Verfügung, die keine Ableitungen benötigen, siehe bei Methoden der lokalen nichtlinearen Optimierung.

Beispiel aus der Enzymkinetik einer nicht linearisierbaren Modellfunktion

Ein Beispiel für Regressionsmodelle, die voll nichtlinear sind, ist die Enzymkinetik. Hier ist zu fordern, dass „nur“ ${\displaystyle y}$ (Reaktionsgeschwindigkeit) und nicht ${\displaystyle \alpha }$ (Substratkonzentration) einem Fehler unterliegt und damit ${\displaystyle \alpha }$ als Variable genutzt werden kann. Die Lineweaver-Burk-Beziehung ist zwar eine algebraisch korrekte Umformung der Michaelis-Menten-Gleichung ${\displaystyle v=V_{\mathrm {max} }\cdot [S]/(K_{m}+[S])}$, ihre Anwendung liefert aber nur korrekte Ergebnisse, wenn die Messwerte fehlerfrei sind. Dies ergibt sich aus der Tatsache, dass sich die Realität nur mit einer erweiterten Michaelis-Menten-Beziehung

${\displaystyle \nu _{i}={\frac {V_{\max }\left[S_{i}\right]}{K_{m}+\left[S_{i}\right]}}(1+e_{i})\ {\boldsymbol {\nu }}_{i}}$

mit ${\displaystyle e_{i}}$ als Fehlerparameter, beschreiben lässt. Diese Gleichung lässt sich nicht mehr linearisieren, also muss hier die Lösung iterativ ermittelt werden.

Fehlverhalten bei Nichterfüllung der Voraussetzungen

Die Methode der kleinsten Quadrate erlaubt es, unter bestimmten Voraussetzungen die wahrscheinlichsten aller Modellparameter zu berechnen. Dazu muss ein korrektes Modell gewählt worden sein, eine ausreichende Menge Messwerte vorliegen und die Abweichungen der Messwerte gegenüber dem Modellsystem müssen eine Normalverteilung bilden. In der Praxis kann die Methode jedoch auch bei Nichterfüllung dieser Voraussetzungen für diverse Zwecke eingesetzt werden. Dennoch sollte beachtet werden, dass die Methode der kleinsten Quadrate unter bestimmten ungünstigen Bedingungen völlig unerwünschte Ergebnisse liefern kann. Beispielsweise sollten keine Ausreißer in den Messwerten vorliegen, da diese das Schätzergebnis verzerren. Außerdem ist Multikollinearität zwischen den zu schätzenden Parametern ungünstig, da diese numerische Probleme verursacht. Im Übrigen können auch Regressoren, die weit von den anderen entfernt liegen, die Ergebnisse der Ausgleichsrechnung stark beeinflussen. Man spricht hier von Werten mit großer Hebelkraft (englisch High Leverage Value).

Multikollinearität

Das Phänomen der Multikollinearität entsteht, wenn die Messreihen zweier gegebener Variablen ${\displaystyle x_{i}}$ und ${\displaystyle x_{j}}$ sehr hoch korreliert sind, also fast linear abhängig sind. Im linearen Fall bedeutet dies, dass die Determinante der Normalgleichungsmatrix ${\displaystyle A^{T}A}$ sehr klein und die Norm der Inversen umgekehrt sehr groß ist; die Kondition von ${\displaystyle A^{T}A}$ ist also stark beeinträchtigt. Die Normalgleichungen sind dann numerisch schwer zu lösen. Die Lösungswerte können unplausibel groß werden, und bereits kleine Änderungen in den Beobachtungen bewirken große Änderungen in den Schätzwerten.

Ausreißer

Ausreißer von y:
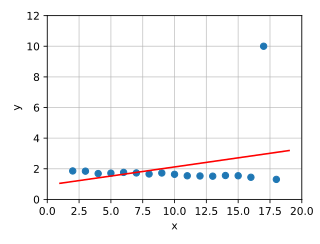
Der Wert zieht die Gerade nach oben

Als Ausreißer sind Datenwerte definiert, die „nicht in eine Messreihe passen“. Diese Werte beeinflussen die Berechnung der Parameter stark und verfälschen das Ergebnis. Um dies zu vermeiden, müssen die Daten auf fehlerhafte Beobachtungen untersucht werden. Die entdeckten Ausreißer können beispielsweise aus der Messreihe ausgeschieden werden oder es sind alternative ausreißerresistente Berechnungsverfahren wie gewichtete Regression oder das Drei-Gruppen-Verfahren anzuwenden.

Im ersten Fall wird nach der ersten Berechnung der Schätzwerte durch statistische Tests geprüft, ob Ausreißer in einzelnen Messwerten vorliegen. Diese Messwerte werden dann ausgeschieden und die Schätzwerte erneut berechnet. Dieses Verfahren eignet sich dann, wenn nur wenige Ausreißer vorliegen.

Bei der gewichteten Regression werden die abhängigen Variablen ${\displaystyle y}$ in Abhängigkeit von ihren Residuen gewichtet. Ausreißer, d. h. Beobachtungen mit großen Residuen, erhalten ein geringes Gewicht, das je nach Größe des Residuums abgestuft sein kann. Beim Algorithmus nach Mosteller und Tukey (1977), der als „biweighting“ bezeichnet wird, werden unproblematische Werte mit 1 und Ausreißer mit 0 gewichtet, was die Unterdrückung des Ausreißers bedingt. Bei der gewichteten Regression sind in der Regel mehrere Iterationsschritte erforderlich, bis sich die Menge der erkannten Ausreißer nicht mehr ändert.

Heteroskedastische Fehler

Liegen heteroskedastische Fehler vor, so liefert die Minimierung des Mittelwertes der kleinsten Quadrate keinen effizienten Schätzer des (bedingten) Mittelwertes, obwohl dieser immer noch unverzerrt ist^[19]. Die Minimierung der Gausschen Negativen Log-Likelihood kann in diesem Fall eine Alternative sein.

Verallgemeinerte Kleinste-Quadrate-Modelle

Weicht man die starken Anforderungen im Verfahren an die Fehlerterme auf, erhält man so genannte verallgemeinerte Kleinste-Quadrate-Ansätze. Wichtige Spezialfälle haben dann wieder eigene Namen, etwa die gewichtete Methode der kleinsten Quadrate (englisch weighted least squares, kurz WLS), bei denen die Fehler zwar weiter als unkorreliert angenommen werden, aber nicht mehr von gleicher Varianz. Dies führt auf ein Problem der Form

${\displaystyle \|D(A\alpha -y)\|_{2},}$

wobei D eine Diagonalmatrix ist. Variieren die Varianzen stark, so haben die entsprechenden Normalgleichungen eine sehr große Kondition, weswegen das Problem direkt gelöst werden sollte.

Nimmt man noch weiter an, dass die Fehler in den Messdaten auch in der Modellfunktion berücksichtigt werden sollten, ergeben sich die „totalen kleinsten Quadrate“ in der Form

${\displaystyle \min _{E,r}\|(E,r)\|_{F},(A+E)\alpha =b+r,}$

wobei ${\displaystyle E}$ der Fehler im Modell und ${\displaystyle r}$ der Fehler in den Daten ist.^[20][21]

Schließlich gibt es noch die Möglichkeit, keine Normalverteilung zugrunde zu legen. Dies entspricht beispielsweise der Minimierung nicht in der euklidischen Norm, sondern der Summennorm. Solche Modelle sind Themen der Regressionsanalyse.

Literatur

• Åke Björck: Numerical Methods for Least Squares Problems. SIAM, Philadelphia 1996, ISBN 0-89871-360-9.
• Walter Großmann: Grundzüge der Ausgleichsrechnung. 3. erw. Auflage. Springer Verlag, Berlin / Heidelberg / New York 1969, ISBN 3-540-04495-7.
• Richard J. Hanson, Charles L. Lawson: Solving least squares problems. SIAM, Philadelphia 1995, ISBN 0-89871-356-0.
• Frederick Mosteller, John W. Tukey: Data Analysis and Regression – a second course in statistics. Addison-Wesley, Reading MA 1977, ISBN 0-201-04854-X.
• Gerhard Opfer: Numerische Mathematik für Anfänger. Eine Einführung für Mathematiker, Ingenieure und Informatiker. 4. Auflage. Vieweg, Braunschweig 2002, ISBN 3-528-37265-6.
• Peter Schönfeld: Methoden der Ökonometrie. 2 Bände. Vahlen, Berlin/Frankfurt 1969–1971.
• Eberhard Zeidler (Hrsg.): Taschenbuch der Mathematik. Begründet v. I.N. Bronstein, K.A. Semendjajew. Teubner, Stuttgart/Leipzig/Wiesbaden 2003, ISBN 3-8171-2005-2.
• T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). 2nd edition. Springer Vieweg, 2016, ISBN 978-3-658-11455-8.

Weblinks

Wikibooks: Beweis zur Methode der kleinsten Fehlerquadrate

Wikibooks: Einführung in die Regressionsrechnung – Lern- und Lehrmaterialien

Einzelnachweise

1. Göttingen. In: Göttingische Anzeigen von Gelehrten Sachen / Göttingische Anzeigen von gelehrten Sachen / Göttingische gelehrte Anzeigen, 23. Jänner 1802, S. 1 (online bei ANNO).Vorlage:ANNO/Wartung/gas
2. Moritz Cantor: Gauß: Karl Friedrich G. In: Allgemeine Deutsche Biographie (ADB). Band 8, Duncker & Humblot, Leipzig 1878, S. 430–445., hier S. 436.
3. Paul Karlson: Zauber der Zahlen. Ullstein-Verlag, Berlin–West. Neunte, überarbeitete und erweiterte Auflage, 1967, S. 390 f.
4. A. Abdulle, Gerhard Wanner: 200 years of least square methods. In: Elemente der Mathematik, Band 57, 2002, S. 45–60, doi:10.1007/PL00000559.
5. Vgl. Moritz Cantor: Gauß: Karl Friedrich G. In: Allgemeine Deutsche Biographie (ADB). Band 8, Duncker & Humblot, Leipzig 1878, S. 430–445., S. 436.
6. Adrien-Marie Legendre: Nouvelles méthodes pour la détermination des orbites des comètes. Paris 1805, S. 72–80 (Anhang): Sur la Méthode des moindres quarrés.
7. Carl Friedrich Gauß: Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium. Göttingen 1809; Carl Haase (Übers.): Theorie der Bewegung der Himmelskörper, welche in Kegelschnitten die Sonne umlaufen. Hannover 1865.
8. Matrices and determinants.
9. Abgedruckt in Gauß, Werke, Band X/1, S. 380.
10. Abdulle, Wanner: Elemente der Mathematik. Band 57, 2002, S. 51. Mit Faksimileabdruck des Tagebucheintrags.
11. Laplace, zitiert nach Herman Goldstine: A history of numerical analysis. Springer, 1977, S. 209.
12. Carl Friedrich Gauß: Theoria combinationis observationum erroribus minimis obnoxiae. 2 Teile. Göttingen 1821–1823 (Commentationes Societatis Regiae Scientiarum Gottingensis recentiores, classis mathematicae, Band 5.); Supplementum Theoria combinationis observationum erroribus minimis obnoxiae. Göttingen 1826/28 (Commentationes Societatis Regiae Scientiarum Gottingensis recentiores, classis mathematicae, Band 6.). Anton Börsch Paul Simon (Hrsg.): Abhandlungen zur Methode der kleinsten Quadrate von Carl Friedrich Gauss. In deutscher Sprache. Berlin 1887, Textarchiv – Internet Archive.
13. Pete Stewart: Maybe We Should Call It “Lagrangian Elimination”. NA Digest Sunday, 21. Juni 1991, June 30, 1991 Volume 91, Issue 26.
14. Applied Regression Analysis and Generalized Linear Models, John Fox, 2015, ISBN 978-1-4833-2131-8, Google Books
15. H. Wirths: Beziehungshaltige Mathematik in Regression und Korrelation. In: Stochastik in der Schule, 1991, Heft 1, S. 34–53
16. D. Britzger: The Linear Template Fit. In: Eur. Phys. J. C. Band 82, 2022, S. 731, doi:10.1140/epjc/s10052-022-10581-w, arxiv:2112.01548.
17. Hans R. Schwarz, Norbert Köckler: Numerische Mathematik. 7. überarb. Auflage. Teubner, 2009, doi:10.1007/978-3-8348-9282-9, ISBN 978-3-8348-9282-9, S. 141, Kapitel 3.6 (Gauß-Approximation), Satz 3.23.
18. A.E. Hoerl and R.W. Kennard: Ridge regression: Biased estimation for nonorthogonal problems, Technometrics 12 (1970), 55-82.
19. The SAGE Encyclopedia of Research Design, ISBN ISBN 978-1-0718-1210-5, Seite 1291, Google books
20. Sabine Van Huffel, Joos Vandewalle: The Total Least Squares Problem: Computational Aspects and Analysis. SIAM Publications, Philadelphia PA 1991, ISBN 0-89871-275-0.
21. Martin Plesinger: The Total Least Squares Problem and Reduction of Data in AX ≈ B. Dissertation. (Memento vom 24. Juli 2012 im Internet Archive; PDF; 1,6 MB) TU Liberec und ICS Prague, 2008.

Dieser Artikel wurde am 27. August 2009 in dieser Version in die Liste der lesenswerten Artikel aufgenommen.