Schwingkreis

Ein elektrischer Schwingkreis, auch als Resonanzkreis bezeichnet, ist eine resonanzfähige elektrische Schaltung aus einer Spule (Bauteil L) und einem Kondensator (Bauteil C), die elektrische Schwingungen ausführen kann (vgl. Abb. 1). Der elektrische Schwingkreis wird oft mit dem harmonischen Oszillator der Mechanik wie dem Federpendel oder der Stimmgabel verglichen. Bei diesem LC-Schwingkreis wird Energie zwischen dem magnetischen Feld der Spule und dem elektrischen Feld des Kondensators periodisch ausgetauscht, wodurch abwechselnd hohe Stromstärke oder hohe Spannung vorliegen. Die Resonanzfrequenz (für Reihen- und idealen Parallelschwingkreis) berechnet sich zu:

${\displaystyle f_{r}={\frac {1}{2\pi {\sqrt {LC}}}}\ ,}$

wobei ${\displaystyle L}$ für die Induktivität der Spule und ${\displaystyle C}$ für die Kapazität des Kondensators stehen. Diese Gleichung heißt Thomsonsche Schwingungsgleichung.

Wird ein Schwingkreis durch einen Schaltvorgang oder einen Impuls einmalig angestoßen, dann führt er freie Schwingungen (Eigenschwingungen) aus, die in der Realität aufgrund von Verlusten nach einer gewissen Zeit abklingen. Wird er jedoch im Bereich seiner Resonanzfrequenz periodisch erregt, dann führt er erzwungene Schwingungen aus. Die dabei auftretenden Resonanzerscheinungen haben für die praktische Anwendung überragende Bedeutung.

Bei einem Schwingkreis mit äußerer Anregung unterscheidet man je nach Anordnung in Bezug zur Anregungsquelle zwischen Parallelschwingkreis (L parallel zu C) und Reihenschwingkreis (L in Reihe zu C). Unpräzise wird der Reihenschwingkreis manchmal auch als Serienschwingkreis bezeichnet.

Ähnliche Schaltungen aus Spule und Kondensator werden auch als LC-Glieder bezeichnet, sie befinden sich jedoch nicht zwingend in Resonanz (siehe Tiefpass, Hochpass).

Abb. 1 Allgemeiner Schwing­kreis, Darstellung mit Schalt­zeichen gemäß EN 60617-4:1996

Physikalische Vorgänge in elektrischen Schwingkreisen

Im Folgenden werden die in elektrischen Schwingkreisen periodisch ablaufenden physikalischen Vorgänge beschrieben. Die grundlegenden Abläufe bei ungedämpften freien und schwach gedämpften erzwungenen Schwingungen im stationären Zustand sind im Wesentlichen dieselben. Hauptmerkmal ist die Konstanz der Gesamtenergie im Schwingkreis, die zwischen Kondensator und Spule hin- und herpendelt (vgl. Abb. 5). Im schwach gedämpften freien Schwingkreis nimmt die Gesamtenergie des Systems hingegen beim Hin- und Herpendeln aufgrund von Verlusten an die Umgebung ab (vgl. Abb. 6). Die folgende Beschreibung beschränkt sich auf den ungedämpften freien Schwingkreis und beginnt mit einem willkürlich gewählten Anfangszustand (vgl. Abb. 2).

Abb. 2 U: Spannung; I: Strom; W: Energie

Abb. 3 Spannungsverlauf (blau gestrichelt) und Stromverlauf (rote Linie) im Schwingkreis

1. Zunächst sei die Spule ohne magnetischen Fluss. Der Kondensator sei geladen und in seinem elektrischen Feld die gesamte Energie des Schwingkreises gespeichert. Noch fließe kein Strom durch die Spule und die Kondensatorspannung sei maximal (Bild 1).
2. Aufgrund der Kondensatorspannung setze nun ein Stromfluss ein, der nach der Lenz’schen Regel eine entgegengesetzt gleich große Spannung an der Spule induziert, die dessen Änderung entgegenwirkt. Damit steigen Stromstärke und magnetischer Fluss nur langsam (anfangs linear mit der Zeit) an. Mit ansteigendem Strom wird im Laufe der Zeit im Kondensator Ladung abgebaut, womit zugleich dessen Spannung absinkt. Mit der Verringerung der Spannung verringert sich das Anwachsen des Stromflusses.
3. Wenn die Spannung auf null abgesunken ist, steigen Strom und magnetischer Fluss nicht mehr an, beide erreichen ihr Maximum. Zu diesem Zeitpunkt ist auch die magnetische Feldstärke der Spule am größten und der Kondensator vollständig entladen. Die gesamte Energie ist nun im Magnetfeld der Spule gespeichert. (Bild 2)
4. Bei spannungsfreier Spule fließt der Strom stetig weiter, da er sich – genau wie der Magnetfluss – nicht abrupt ändern kann. Der Strom beginnt, den Kondensator in Gegenrichtung zu laden und baut in ihm eine Spannung ebenfalls in Gegenrichtung auf (anfangs linear mit der Zeit), die den Strom und somit auch den magnetischen Fluss verringern. Dies verursacht nach der Lenz’schen Regel eine entgegengesetzt gleich große Spannung an der Spule, die die Verringerung von Strom und magnetischen Fluss zu verhindern sucht.
5. Wenn die Stromstärke auf null zurückgegangen ist, steigt der Betrag der Spannung nicht mehr an und erreicht somit sein Maximum. Der Kondensator erlangt seine ursprüngliche Ladung wieder, allerdings bei entgegengesetzter Polung. Die gesamte magnetische Feldenergie ist wieder in elektrische Feldenergie überführt worden. (Bild 3)
6. Diese Vorgänge setzen sich in entgegengesetzter Richtung fort. (Bild 4, dann wieder Bild 1)

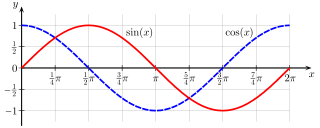
Der periodische Strom-Spannungs-Verlauf folgt der Sinus- bzw. Kosinusfunktion gemäß Abb. 3. Der Übergang von Bild 1 zu Bild 2 entspricht in den Funktionen dem Bereich x = 0 … π/2; der Übergang von Bild 2 zu Bild 3 verläuft wie im Bereich x = π/2 … π, von Bild 3 über Bild 4 zu Bild 1 wie in x = π … 2π.

Freie Schwingungen in elektrischen Schwingkreisen

Abb. 4 Freier Reihenschwingkreis. Maschenregel liefert ${\displaystyle u_{C}+Ri+L{\frac {di}{dt}}=0}$

In erster Näherung kann man die in Schwingkreisen auftretenden Verluste durch einen ohmschen Widerstand R darstellen, der in Reihe mit der Induktivität L liegt. Ausgehend vom Maschensatz und dem Verhalten der drei Bauelemente (Bepfeilung wie in Abb. 4) kann ein solcher RLC-Reihenschwingkreis durch folgendes (lineares) Differentialgleichungssystem beschrieben werden:

${\displaystyle u_{C}+R\cdot i+L\cdot {\frac {di}{dt}}=0}$

${\displaystyle C\cdot {\frac {du_{C}}{dt}}=i}$

Durch Eliminieren von u_C erhält man eine lineare Differentialgleichung zweiter Ordnung für den Strom:

${\displaystyle LC\cdot {\frac {d^{2}i}{dt^{2}}}+RC\cdot {\frac {di}{dt}}+i=0\quad }$ bzw. ${\displaystyle \quad {\frac {d^{2}i}{dt^{2}}}+2\delta \cdot {\frac {di}{dt}}+\omega _{0}^{2}\cdot i=0}$

wobei die „Abkürzungen“ für die ungedämpfte Eigenkreisfrequenz ${\displaystyle \omega _{0}={\frac {1}{\sqrt {LC}}}}$ und für den Dämpfungskoeffizienten ${\displaystyle \delta ={\frac {R}{2L}}}$ benutzt wurden.

Die Differentialgleichung für die Kondensatorspannung hat die gleiche Form. Für die zur eindeutigen Lösung benötigten zwei Anfangsbedingungen nimmt man meist an, dass zum Zeitpunkt t=0 der Kondensator mit einer Spannung u_C0 aufgeladen und der Strom durch die Induktivität 0 ist.

Im Folgenden werden die Lösungen für die verschiedenen Fälle angegeben. Deren Richtigkeit kann durch Einsetzen in die Differentialgleichungen und durch Kontrolle des Anfangszustandes überprüft werden.

Der ungedämpfte freie Schwingkreis

Für den verlustfreien Schwingkreis ist ${\displaystyle R=0}$ bzw. ${\displaystyle \delta =0}$, sodass das Dämpfungsglied in obiger Differentialgleichung entfällt. Die Lösungen sind ungedämpfte harmonische (um 90° phasenverschobenen) Schwingungen (vgl. Abb. 3)

${\displaystyle i(t)=-{\frac {u_{C0}}{\omega _{0}L}}\cdot \sin {\omega _{0}t}}$

${\displaystyle u_{C}(t)=u_{C0}\cdot \cos {\omega _{0}t}}$

Der gedämpfte freie Reihenschwingkreis

Bei verlustbehafteten Schwingkreisen ist ${\displaystyle R\neq 0}$ bzw. ${\displaystyle \delta \neq 0}$, sodass das Dämpfungsglied in obiger Differentialgleichung nicht entfällt. Hier unterscheidet man drei Fälle.

Schwingfall

Bei geringen Verlusten im Schwingkreis, d. h. ${\displaystyle \delta <\omega _{0}}$, lauten die Lösungen

${\displaystyle i(t)=-{\frac {u_{C0}}{\omega _{d}L}}\cdot e^{-\delta t}\cdot \sin {\omega _{d}t}}$

${\displaystyle u_{C}(t)=u_{C0}\cdot e^{-\delta t}\cdot \left(\cos {\omega _{d}t+{\frac {\delta }{\omega _{d}}}\cdot \sin {\omega _{d}t}}\right)=u_{C0}\cdot {\frac {\omega _{d}}{\omega _{0}}}\cdot e^{-\delta t}\cdot \cos \left({\omega _{d}t-\varphi }\right)}$

Hierbei ist ${\displaystyle \omega _{d}={\sqrt {\omega _{0}^{2}-\delta ^{2}}}}$ die gedämpfte Eigenkreisfrequenz und ${\displaystyle \varphi =\arctan {\frac {\delta }{\omega _{d}}}}$ die Phasenverschiebung.

In diesem „Normalfall der Praxis“ sind Strom und Kondensatorspannung durch den Faktor ${\displaystyle e^{-\delta t}}$ schwach gedämpft und nicht genau gegeneinander 90° in der Phase verschoben; die gedämpfte Eigenkreisfrequenz ω_d liegt unterhalb der ungedämpften Eigenkreisfrequenz ω₀.

Kriechfall

Bei großen Verlusten, d. h. ${\displaystyle \delta >\omega _{0}}$, entsteht keine Schwingung mehr. Je größer die Dämpfung ist, umso langsamer kriechen Strom und Spannung gegen 0. Im sog. Kriechfall lauten die Lösungen

${\displaystyle i(t)=-{\frac {u_{C0}}{\kappa L}}\cdot e^{-\delta t}\cdot \sinh {\kappa t}}$

${\displaystyle u_{C}(t)=u_{C0}\cdot e^{-\delta t}\cdot \left(\cosh {\kappa t+{\frac {\delta }{\kappa }}\cdot \sinh {\kappa t}}\right)=u_{C0}\cdot {\frac {\omega _{0}}{\kappa }}\cdot e^{-\delta t}\cdot \sinh \left({\kappa t+\chi }\right)}$

wobei ${\displaystyle \kappa ={\sqrt {\delta ^{2}-\omega _{0}^{2}}}}$ die „Kriechkonstante“ ist und ${\displaystyle \chi =\operatorname {arcoth} {\frac {\delta }{\kappa }}}$ die „hyperbolische“ Phasenverschiebung.

Aperiodischer Grenzfall

Auch im aperiodischen Grenzfall ${\displaystyle \delta =\omega _{0}}$ findet keine Schwingung mehr statt. Der Ruhezustand wird hier „ohne Überschwingen“ am schnellsten wiedererreicht. Hier lauten die Lösungen

${\displaystyle i(t)=-{\frac {u_{C0}}{L}}\cdot t\cdot e^{-\delta t}}$

${\displaystyle u_{C}(t)=u_{C0}\cdot \left(1+\delta t\right)\cdot e^{-\delta t}}$

Energiebilanz für den freien Schwingkreis

Abb. 5 Energie-Zeit-Diagramm des freien Reihenschwingkreises ohne Dämpfung

Abb. 6 Energie-Zeit-Diagramm des freien Reihenkreises bei schwacher Dämpfung

Die Gesamtenergie des Systems ${\displaystyle E=E_{C}+E_{L}}$ besteht aus der Summe von elektrischer Feldenergie des Kondensators ${\displaystyle E_{C}={\frac {1}{2}}Cu_{C}^{2}}$ und magnetischer Feldenergie der Spule ${\displaystyle E_{L}={\frac {1}{2}}Li^{2}}$. Differentiation liefert

${\displaystyle {\frac {dE}{dt}}=C\,u_{C}\,{\frac {du_{C}}{dt}}+L\,i\,{\frac {di}{dt}}=\left(u_{C}+L{\frac {di}{dt}}\right)i=-Ri^{2}}$

wobei in den letzten beiden Schritten beide Gleichungen des obigen Differentialgleichungssystems eingesetzt wurden.

Fall ${\displaystyle R=0}$: Die Gleichung ${\displaystyle {\dot {E}}=0}$ besagt, dass die Gesamtenergie im ungedämpften freien Schwingkreis konstant bleibt, d. h. ${\displaystyle E(t)=E_{0}={\frac {1}{2}}Cu_{C0}^{2}}$, und verlustfrei zwischen Kondensator und Spule hin- und herpendelt (vgl. Abb. 5).

Fall ${\displaystyle R\neq 0}$: Die Gleichung ${\displaystyle {\dot {E}}=-Ri^{2}}$ besagt, dass die Energie im gedämpften freien Reihenschwingkreis abnimmt, weil beständig Stromwärme dissipiert wird. Die abklingende Energie ist in Abb. 6 beispielhaft für den Fall schwacher Dämpfung dargestellt.

Bei schwacher Dämpfung, d. h. falls ${\displaystyle \delta \ll \omega _{0}=2\pi /T_{0}}$, ist die ungedämpfte Schwingungsperiode ${\displaystyle T_{0}}$ im Vergleich zur Energierelaxationszeit ${\displaystyle \tau =1/2\delta }$ klein, d. h. ${\displaystyle T_{0}\ll \tau }$. Da dann auch ${\displaystyle \omega _{d}\approx \omega _{0}}$, ist die zwischen Kondensator und Spule hin- und herpendelnde Gesamtenergie ${\displaystyle E(t)=E_{0}\,e^{-{\frac {t}{\tau }}}}$. Damit erhält man für die jeweils in der Folgeperiode dissipierte Energie

${\displaystyle W_{V}(t)=E(t)-E(t+T_{0})=\left\{1-e^{-{\frac {T_{0}}{\tau }}}\right\}E(t)\approx {\frac {E(t)}{\tau }}\,T_{0}}$,

wobei die Näherung ${\displaystyle e^{-x}\approx 1-x}$ für ${\displaystyle |x|\ll 1}$ benutzt wurde. Daraus lässt sich die Kreisgüte mithilfe ihrer Energiedefinition berechnen (siehe unten).

Erzwungene Schwingungen in elektrischen Schwingkreisen

Für die Beschreibung erzwungener Schwingungen wird im Folgenden eine Erregung der Schwingkreise durch eine ideale Einspeisequelle angenommen (d. h. in diesem Fall sinusförmige Wechselspannung oder -strom), welche schon solange anliegt, dass die Eigenschwingungen durch den Einschaltvorgang aufgrund der Verlustdämpfung abgeklungen sind. Man spricht dann vom stationären oder eingeschwungenen Zustand. Die unten angegebenen Lösungen der Differentialgleichungen beschreiben entsprechend nur den eingeschwungenen Zustand der gedämpften Schwingkreise; für weitergehende Analysen werden dann komplexe Wechselstromrechnung und Zeigerdiagramme genutzt.

Erzwungene Schwingungen im Reihenkreis

Abb. 7 RLC-Reihenschwingkreis. Maschenregel liefert: ${\displaystyle u=u_{C}+R\,i+u_{L}}$

Abb. 8 Amplitudengang des Stroms ${\displaystyle i_{0}(\omega )}$ für verschiedene Güten ${\displaystyle G}$ bei Spannungseinspeisung für ${\displaystyle u_{0}=1\,{\text{V}}}$, ${\displaystyle L=1\,{\text{H}}}$, ${\displaystyle C=1\,{\text{F}}}$

Beim RLC-Reihenkreis liegen Induktivität ${\displaystyle L}$, Kapazität ${\displaystyle C}$ und Verlustwiderstand ${\displaystyle R}$ in Reihe an den Klemmen einer idealen Einspeisequelle (s. o.), die dem Schwingkreis ihre Erregerfrequenz ${\displaystyle \omega }$ aufprägt. Mit dem Maschensatz ergibt sich folgende Gleichung (Bepfeilung wie in Abb. 7)

${\displaystyle u=u_{C}+R\cdot i+u_{L}}$ ${\displaystyle \quad \quad ({\text{M}})}$

wobei ${\displaystyle u_{C}=Q/C}$ und ${\displaystyle u_{L}=L{\frac {di}{dt}}}$. Einsetzen und Differenzieren nach der Zeit ergibt

${\displaystyle {\frac {du}{dt}}={\frac {i}{C}}+R\cdot {\frac {di}{dt}}+L\cdot {\frac {d^{2}i}{dt^{2}}}\quad }$ bzw. ${\displaystyle \quad {\frac {d^{2}i}{dt^{2}}}+2\delta \cdot {\frac {di}{dt}}+\omega _{r}^{2}\cdot i={\frac {1}{L}}{\frac {du}{dt}}}$

mit den Abkürzungen ${\displaystyle \omega _{r}=1/{\sqrt {LC}}}$ für die Resonanzfrequenz des Reihenschwingkreises und ${\displaystyle \delta =R/2L}$ für den Dämpfungskoeffizienten. Dies ist eine lineare Differentialgleichung zweiter Ordnung und lässt sich besonders leicht mit einem komplexen Ansatz lösen. Natürlich muss jede physikalische Lösung reell sein. Aufgrund der Linearität der Gleichung müssen Real- und Imaginärteil einer Lösung jeder für sich die Gleichung lösen und jede reelle Linearkombination reeller Lösungen eine physikalische Lösung ergeben.

Einsetzen des komplexen Ansatzes (imaginäre Einheit hier: ${\displaystyle \mathrm {j} }$)

${\displaystyle {\underline {u}}(t)=u_{0}\cdot e^{\mathrm {j} \omega t}}$, ${\displaystyle \;}$ ${\displaystyle {\underline {i}}(t)=i_{0}\cdot e^{\mathrm {j} (\omega t-\varphi )}}$

in die Differentialgleichung, Division durch ${\displaystyle \mathrm {j} \omega {\underline {i}}}$ sowie anschließendes Sortieren nach Real- und Imaginärteil liefert die Gesamtimpedanz bzw. den Scheinwiderstand

${\displaystyle {\underline {Z}}={\frac {\underline {u}}{\underline {i}}}={\frac {u_{0}}{i_{0}}}\,e^{\mathrm {j} \varphi }=R+\mathrm {j} \underbrace {{\biggl (}\omega L-{\frac {1}{\omega C}}{\biggr )}} _{=X}}$    bzw.    ${\displaystyle Z={\frac {u_{0}}{i_{0}}}={\sqrt {R^{2}+X^{2}}}}$ ${\displaystyle \qquad (*)}$

Die Phasenverschiebung ${\displaystyle \varphi }$ erhält man aus

${\displaystyle \tan \varphi ={\frac {\operatorname {Im} {\underline {Z}}}{\operatorname {Re} {\underline {Z}}}}={\frac {\omega L-{\frac {1}{\omega C}}}{R}}}$

Das reellwertige Paar bestehend aus Klemmenspannung ${\displaystyle u(t):=\operatorname {Re} \{{\underline {u}}(t)\}=u_{0}\cos(\omega t)}$ und Klemmenstrom ${\displaystyle i(t):=\operatorname {Re} \{{\underline {i}}(t)\}=i_{0}\cos(\omega t-\varphi )}$ löst obige Differentialgleichung. Hervorzuheben ist hierbei die Abhängigkeit der Phasenverschiebung ${\displaystyle \varphi =\varphi (\omega )}$ sowie des Scheinwiderstandes ${\displaystyle Z=Z(\omega )}$ von der Erregerfrequenz ${\displaystyle \omega }$. Diese Abhängigkeit lässt sich durch Ortskurven für die Impedanz ${\displaystyle {\underline {Z}}(\omega )=Z(\omega )\,e^{\mathrm {j} \varphi (\omega )}}$ veranschaulichen (vgl. unten). Die Amplituden von Klemmenspannung und -strom hängen gemäß ${\displaystyle (*)}$ über ${\displaystyle u_{0}(\omega )=Z(\omega )\,i_{0}(\omega )}$ zusammen; bei Spannungseinspeisung wird ${\displaystyle u_{0}(\omega )=}$ const., bei Stromeinspeisung ${\displaystyle i_{0}(\omega )=}$ const. angenommen.

Die Frequenz, bei welcher der Scheinwiderstand minimal wird, heißt Resonanzfrequenz des Reihenkreises und stimmt mit der oben so bezeichneten Abkürzung ${\displaystyle \omega _{r}}$ überein, was ihre Bezeichnung rechtfertigt. Die Resonanzbedingung ist ausdrückbar durch

${\displaystyle X=\operatorname {Im} {\underline {Z}}\mathrel {\stackrel {\text{!}}{=}} 0}$

Im Resonanzfall wird dann aufgrund von ${\displaystyle (*)}$ bei Spannungseinspeisung die Stromamplitude maximal ${\displaystyle i_{0}(\omega _{r})=u_{0}/R}$ (vgl. Abb.  8) und umgekehrt bei Stromeinspeisung die Spannungsamplitude minimal. Im Gegensatz zu ihrem mechanischen Pendant hängt die Resonanzfrequenz nicht (!) von der Dämpfung ab. Daher stimmt die Resonanzfrequenz für den Reihenkreis mit der ungedämpften Eigenfrequenz ${\displaystyle \omega _{0}}$ des freien Reihenkreises überein, d. h. es gilt ${\displaystyle \omega _{r}=\omega _{0}=1/{\sqrt {LC}}}$, wie man durch Einsetzen in ${\displaystyle X=X(\omega )}$ bestätigt.

Reihenresonanz (Spannungsüberhöhung)

Abb. 9 Spannung­süberhöhung im Resonanz­fall

Für die komplexen Effektivwerte von Kondensator- und Spulenspannung gilt ${\displaystyle \;{\underline {U}}_{C}=-\mathrm {j} \,{\underline {I}}/\omega C}$ und ${\displaystyle {\underline {U}}_{L}=\mathrm {j} \,\omega L{\underline {I}}}$, wobei ${\displaystyle {\underline {I}}={\underline {U}}/{\underline {Z}}}$ und ${\displaystyle U=u_{0}/{\sqrt {2}}}$ sowie ${\displaystyle I=i_{0}/{\sqrt {2}}}$ .

Nahe der Resonanzfrequenz (d. h. für ${\displaystyle \omega \approx \omega _{r}=\omega _{0}}$) gilt ${\displaystyle X\approx 0}$ und somit ${\displaystyle {\underline {Z}}\approx R}$ (Reihenresonanz). Für die Effektivwerte der Spannungen ergibt sich dann

${\displaystyle U_{C}={\frac {I}{\omega C}}\approx {\frac {1}{R}}{\sqrt {\frac {L}{C}}}\,U\quad }$ und ${\displaystyle \quad U_{L}=\omega LI\approx {\frac {1}{R}}{\sqrt {\frac {L}{C}}}\,U}$

Hieran liest man unmittelbar ab, dass die Effektivwerte der Einzelspannungen an Kondensator und Spule nahe der Resonanzfrequenz den Effektivwert der Klemmenspannung ${\displaystyle U}$ bei geringer Dämpfung (d. h. ${\displaystyle R<{\sqrt {L/C}}}$) überragen. Dieses Verhalten nennt man Spannungsüberhöhung (vgl. Abb. 9) und wird beim Resonanztransformator ausgenutzt.

Ferner sieht man, dass die Spannungsüberhöhung ${\displaystyle U_{C}/U=U_{L}/U}$ durch die Kreisgüte ${\displaystyle Q}$ ausdrückbar ist. Nahe der Resonanzfrequenz gilt

${\displaystyle U_{C}/U=U_{L}/U\approx Q={\frac {1}{R}}{\sqrt {\frac {L}{C}}}}$

Im Resonanzfall wird aus der Näherung exakte Gleichheit.

Die Höhe des Klemmenstroms ${\displaystyle I=U/Z}$ nahe der Resonanzfrequenz wird bei Spannungseinspeisung nur durch ${\displaystyle Z\approx R}$ bestimmt. Im verlustfreien, ungedämpften Grenzfall ${\displaystyle R=0}$ wird daher ${\displaystyle I=\infty }$ und es tritt ein Kurzschluss auf bzw. eine Resonanz­katastrophe ein (vgl. Abb. 8 für ${\displaystyle G=\infty }$); dieses Verhalten wird in Saugkreisen genutzt. Auch die Spannungsüberhöhungen an den Bauteilen wachsen dann über alle Grenzen, weil sie direkt proportional zum Klemmenstrom ${\displaystyle I}$ sind.

Ortskurve für den Reihenkreis

Abb. 10 Ortskurve für den Reihenkreis

Das Verhalten des Reihenkreises bei Veränderung der von außen aufgeprägten Netzfrequenz ${\displaystyle \omega }$ wird durch das Verhalten der Impedanz ${\displaystyle {\underline {Z}}=R+\mathrm {j} X}$ charakterisiert. Graphisch kann das Impedanzverhalten durch eine Ortskurve (vgl. Abb. 10) dargestellt werden.

1. Bei Resonanz (d. h. ${\displaystyle \omega =\omega _{r}}$) ist ${\displaystyle X=0}$, sodass der Zeiger auf der reellen Achse liegt. Die Impedanz stimmt dann mit dem Resonanzwiderstand ${\displaystyle R}$ überein.
2. Unterhalb der Resonanzfrequenz verhält sich der Blindanteil kapazitiv, ${\displaystyle X<0}$, der Zeiger liegt dann unterhalb der reellen Achse;
   oberhalb der Resonanzfrequenz verhält sich die Blindanteil induktiv, ${\displaystyle X>0}$, der Zeiger liegt dann oberhalb der reellen Achse.
3. Die Frequenz ${\displaystyle \omega _{\text{min}}}$, bei der das Minimum des Scheinleitwerts ${\displaystyle Z(\omega _{\text{min}})=Z_{\text{min}}}$ angenommen wird, stimmt mit der Resonanzfrequenz überein, d. h. ${\displaystyle \omega _{\text{min}}=\omega _{r}=\omega _{0}}$. In Abb. 10 stimmen daher auch die entsprechenden Zeiger mit dem Resonanzwiderstand überein, d. h. ${\displaystyle {\underline {Z}}_{\text{min}}={\underline {Z}}(\omega _{0})={\underline {Z}}(\omega _{r})=R}$.
4. Der Wirkanteil der Impedanz ${\displaystyle \operatorname {Re} {\underline {Z}}=R}$ ist frequenzunabhängig. Anschaulich bedeutet dies, dass die Ortskurve eine zur imaginären Achse parallele Gerade sein muss. Umgekehrt hängt daher die Resonanzfrequenz ${\displaystyle \omega _{r}}$ nicht (!) vom Widerstand ${\displaystyle R}$ (d. h. von der Dämpfung ${\displaystyle \delta }$) ab.

Alternativ kann das Verhalten direkt aus ${\displaystyle (*)}$ abgelesen werden.

Energiebilanz für den Reihenkreis

Die gesamte Energie des Systems ${\displaystyle E}$ ergibt sich als Summe von elektrischer Feldenergie des Kondensators ${\displaystyle E_{C}={\frac {1}{2}}Cu_{C}^{2}}$ und magnetischer Feldenergie der Spule ${\displaystyle E_{L}={\frac {1}{2}}Li^{2}}$. Im stationären Zustand muss diese konstant sein, d. h. ${\displaystyle E=E_{C}+E_{L}={\text{const.}}}$ Daraus folgt

${\displaystyle 0={\frac {dE}{dt}}=C\,u_{C}\,{\frac {du_{C}}{dt}}+L\,i\,{\frac {di}{dt}}=(u_{C}+u_{L})i=(u-Ri)i\quad \Leftrightarrow \quad ui=Ri^{2}}$

wobei im vorletzten Schritt die Maschengleichung ${\displaystyle ({\text{M}})}$ ausgenutzt wurde.

Im ungedämpften Fall ${\displaystyle R=0}$ besagt die Gleichung, dass keine Energie verheizt wird. Solange ${\displaystyle \omega \neq \omega _{r}}$ ergibt sich ein wohlbestimmter stationärer Zustand mit konstanter Gesamtenergie im Schwingkreis. Die Energie wächst nicht über alle Grenzen, weil Klemmenspannung ${\displaystyle u(t)}$ und Klemmenstrom ${\displaystyle i(t)}$ nicht in Phase schwingen. Im Resonanzfall schwingen sie jedoch in Phase, sodass beständig Energie ins System hineinfließt; die Gesamtenergie im System wächst dann theoretisch über alle Grenzen und es ergibt sich hier kein stationärer Zustand mehr.

Im gedämpften Fall ${\displaystyle R\neq 0}$ besagt die Gleichung, dass die von außen zugeführte Leistung ${\displaystyle P_{e}={\overline {ui}}=UI\cos \varphi }$ im stationären Zustand als ohmsche Verlustleistung ${\displaystyle P_{V}={\overline {Ri^{2}}}=RI^{2}}$ verheizt wird, wobei ${\displaystyle U=u_{0}/{\sqrt {2}}}$ und ${\displaystyle I=i_{0}/{\sqrt {2}}}$. Anders ausgedrückt: Während die Gesamtenergie ${\displaystyle E=LI^{2}}$ zwischen Kondensator und Spule hin- und herpendelt, wird beständig Stromwärme an die Umgebung abgegeben. Die dissipierte Energie wird von der äußeren Energiequelle nachgeliefert, sodass die Gesamtenergie im System konstant bleibt. Aus ${\displaystyle E,P_{V}}$ und ${\displaystyle \omega _{r}}$ lässt sich die Kreisgüte mithilfe ihrer Energiedefinition berechnen (siehe unten).

Erzwungene Schwingungen im Parallelkreis

Abb. 11 RLC-Parallelschwingkreis mit verlustbehafteter Spule

Im RLC-Parallelschwingkreis liegen Kapazität ${\displaystyle C}$ und Induktivität ${\displaystyle L}$ parallel an den Klemmen einer idealen Einspeisequelle (vgl. Reihenkreis), die dem Schwingkreis ihre Erregerfrequenz ${\displaystyle \omega }$ aufprägt. Verluste der Spule werden durch eine Reihenersatzschaltung von Induktivität ${\displaystyle L}$ und ohmschen Widerstand ${\displaystyle R_{L}}$ (vgl. Abb. 11) modelliert und alle weiteren Verluste vernachlässigt (z. B. Stromwärme in Leitungen, dielektrische Erwärmung des Kondensators, Abstrahlung von EM-Wellen). Wie beim Reihenkreis wird bei Spannungseinspeisung ${\displaystyle u_{0}(\omega )=}$ const., bei Stromeinspeisung ${\displaystyle i_{0}(\omega )=}$ const. angenommen.

Um die Dualitätsbeziehungen in allem, was folgt, ausnützen zu können, wird ein Parallelersatzschaltbild genutzt, sodass alle Bauteile (Kapazität ${\displaystyle C}$, Induktivität ${\displaystyle L_{p}}$ und Widerstand ${\displaystyle R_{p}=1/G_{p}}$) parallel an den Klemmen der idealen Einspeisequelle liegen (vgl. Abb. 11), dies ergibt das zum Reihenkreis duale Netzwerk (vgl. Abb. 12). Der verlustfreie Grenzfall ${\displaystyle R_{L}=0}$ entspricht hierbei ${\displaystyle G_{p}=0}$. Für die Rücktransformation aller durch duale Ersetzung erhaltenen Ergebnisse und Gleichungen in das „ursprüngliche“ Reihenersatzschaltmodell für die verlustbehaftete Spule nutzt man folgende Transformationsformeln (vgl. Abb. 11):

${\displaystyle G_{p}={\frac {R_{L}}{R_{L}^{2}+\omega ^{2}L^{2}}}}$ und ${\displaystyle L_{p}=L+{\frac {R_{L}^{2}}{\omega ^{2}L}}}$ ${\displaystyle \qquad ({\text{TF}})}$

Abb. 12 Dualität von Parallel- und Reihenschwingkreis

Durch duale Ersetzung kann man ohne weitere Rechnung alle Formeln und Ergebnisse aus dem Reihenkreis übernehmen, indem man gemäß Abb. 12 überall die Buchstaben für Spannungen ${\displaystyle u}$ und Ströme ${\displaystyle i}$ vertauscht (${\displaystyle u\leftrightarrow i}$, ${\displaystyle u_{C}\leftrightarrow i_{C}}$ usw.) sowie jedes Schaltelement durch sein duales Pendant ersetzt (${\displaystyle L\leftrightarrow C}$, ${\displaystyle C\leftrightarrow L_{p}}$, ${\displaystyle R\leftrightarrow G_{p}}$, ${\displaystyle X\leftrightarrow B_{p}}$ sowie ${\displaystyle {\underline {Z}}\leftrightarrow {\underline {Y}}_{p}}$). Selbstverständlich führt das Lösen der zugehörigen Differentialgleichung zu denselben Ergebnissen, das duale Ersetzungsschema ist lediglich eine „Abkürzung“.

Duales Ersetzen liefert die Knotengleichung

${\displaystyle i=i_{C}+i_{L_{p}}+i_{G_{p}}}$ ${\displaystyle \qquad ({\text{K}})}$

wobei ${\displaystyle i_{C}=C{\frac {du}{dt}}}$ und ${\displaystyle u=L_{p}{\frac {di_{L_{p}}}{dt}}=i_{G_{p}}/G_{p}}$.

Für die Gesamtadmittanz und den Scheinleitwert erhält man

${\displaystyle {\underline {Y}}_{p}={\frac {\underline {i}}{\underline {u}}}={\frac {i_{0}}{u_{0}}}\,e^{-\mathrm {j} \varphi }=G_{p}+\mathrm {j} \underbrace {{\biggl (}\omega C-{\frac {1}{\omega L_{p}}}{\biggr )}} _{=B_{p}}}$    bzw.    ${\displaystyle Y_{p}={\frac {i_{0}}{u_{0}}}={\sqrt {G_{p}^{2}+B_{p}^{2}}}}$ ${\displaystyle \qquad (*{\scriptstyle {\text{P}}})\quad }$

Für die duale Resonanzbedingung erhält man

${\displaystyle B_{p}=\operatorname {Im} {\underline {Y}}_{p}\mathrel {\stackrel {\text{!}}{=}} 0}$

für die Resonanzfrequenz des Parallelkreises ${\displaystyle \omega _{r}=1/{\sqrt {L_{p}C}}}$ und den Dämpfungskoeffizienten ${\displaystyle \delta ={\frac {G_{p}}{2C}}}$. Bei Resonanzfrequenz nimmt der Scheinleitwert ein Minimum an; gemäß ${\displaystyle (*{\scriptstyle {\text{P}}})}$ hängen die Amplituden von Klemmenstrom und -spannung über ${\displaystyle i_{0}(\omega )=Y_{p}(\omega )\,u_{0}(\omega )}$ zusammen, so dass im Resonanzfall bei Stromeinspeisung die Spannungsamplitude maximal wird und umgekehrt bei Spannungseinspeisung die Stromamplitude minimal.

Mithilfe von ${\displaystyle ({\text{TF}})}$ und der ungedämpften Eigenfrequenz ${\displaystyle \omega _{0}=1/{\sqrt {LC}}}$ ist die Resonanzfrequenz ausdrückbar durch

${\displaystyle \omega _{r}={\frac {1}{\sqrt {L_{p}C}}}=\omega _{0}{\sqrt {1-{\frac {R_{L}^{2}C}{L}}}}}$ ${\displaystyle \qquad ({\text{RF}})}$

Im Gegensatz zum Reihenschwingkreis hängt die Resonanzfrequenz des Parallelschwingkreises im Allgemeinen vom ohmschen Widerstand ${\displaystyle R_{L}}$ ab und liegt deshalb unterhalb der ungedämpften Eigenfrequenz ${\displaystyle \omega _{0}}$ freier Schwingungen. Bei schwacher Dämpfung kann man die Widerstandsabhängigkeit jedoch vernachlässigen, sodass ${\displaystyle \omega _{r}\approx \omega _{0}}$. Nur im Grenzfall ${\displaystyle R_{L}=0}$ gilt exakt ${\displaystyle \omega _{r}=\omega _{0}}$.

Die Diskussionen in den folgenden Abschnitten Parallelresonanz, Ortskurve, Energiebilanz und Kreisgüte verlaufen aufgrund der Dualität ähnlich zum Reihenkreis, lediglich die Abhängigkeit von der Erregerfrequenz ist bei ${\displaystyle G_{p}}$ und ${\displaystyle L_{p}}$ über ${\displaystyle ({\text{TF}})}$ zu berücksichtigen.

Parallelresonanz (Stromüberhöhung)

Abb. 13 Strom­über­höhung im Resonanz­fall bei schwacher Dämpfung

Die dualen Beziehungen für die komplexen Effektivwerte lauten ${\displaystyle \;{\underline {I}}_{L_{p}}=-\mathrm {j} \,{\underline {U}}/\omega L_{p}}$, ${\displaystyle \;{\underline {I}}_{C}=\mathrm {j} \,\omega C{\underline {U}}}$, ${\displaystyle \;{\underline {I}}_{G_{p}}=G_{p}\,{\underline {U}}}$ sowie ${\displaystyle {\underline {I}}={\underline {Y}}_{p}\,{\underline {U}}}$, wobei ${\displaystyle U=u_{0}/{\sqrt {2}}}$ und ${\displaystyle I=i_{0}/{\sqrt {2}}}$ .

Einsetzen der Resonanzfrequenz in die obigen Transformationsformeln ${\displaystyle ({\text{TF}})}$ liefert den Resonanzleitwert und die Resonanzinduktivität für die Parallelersatzschaltung in Abhängigkeit vom Verlustwiderstand ${\displaystyle R_{L}}$

${\displaystyle G_{pr}:={\frac {R_{L}C}{L}}\quad }$ und ${\displaystyle \quad L_{pr}:={\frac {L^{2}}{L-R_{L}^{2}C}}=L{\biggl (}{\frac {\omega _{0}}{\omega _{r}}}{\biggr )}^{2}}$

wobei ${\displaystyle \omega _{0}=1/{\sqrt {LC}}}$ die ungedämpfte Eigenfrequenz ist. Im Resonanzfall wird der Dämpfungskoeffizient somit zu ${\displaystyle \delta _{r}={\frac {G_{pr}}{2C}}={\frac {R_{L}}{2L}}}$ und die Resonanzfrequenz lässt sich entsprechend ausdrücken durch ${\displaystyle \omega _{r}={\sqrt {\omega _{0}^{2}-4\delta _{r}^{2}}}}$.

Nahe der Resonanzfrequenz (d. h. für ${\displaystyle \omega \approx \omega _{r}}$) ist ${\displaystyle G_{p}\approx G_{pr}}$ und ${\displaystyle L_{p}\approx L_{pr}}$; ferner ${\displaystyle B_{p}\approx 0}$ und somit ${\displaystyle {\underline {Y}}_{p}\approx G_{pr}}$(Parallelresonanz). Bei schwacher Dämpfung, d. h. ${\displaystyle \delta _{r}\ll \omega _{0}}$, gilt ${\displaystyle \omega _{r}\approx \omega _{0}}$ und ${\displaystyle L_{pr}\approx L}$. Damit ergibt sich für die Effektivwerte der Ströme durch Spule und Kondensator im Parallelersatzschaltbild

${\displaystyle I_{L_{p}}={\frac {U}{\omega L_{p}}}\approx {\frac {I}{\omega _{0}L\,G_{pr}}}=QI\quad }$ und ${\displaystyle \quad I_{C}=\omega C\,U\approx {\frac {\omega _{0}C}{G_{pr}}}\,I=QI}$

wobei ${\displaystyle Q={\frac {1}{R_{L}}}{\sqrt {\frac {L}{C}}}}$ die Kreisgüte ist.

Um die Stromüberhöhung für die verlustbehaftete Spule im eigentlichen Modell (vgl. Abb. 11 Reihenersatzschaltung links) zu erhalten, muss noch die Beziehung ${\displaystyle {\underline {I}}_{L}={\underline {I}}_{G_{p}}+{\underline {I}}_{L_{p}}}$ berücksichtigt werden (für den Kondensator gilt obiges Resultat auch im Reihenersatzschaltmodell, weil er als verlustfrei angenommen und somit keiner Transformation unterworfen wird). Unter den gleichen Voraussetzungen wie oben erhält man mit ${\displaystyle {\underline {I}}_{G_{p}}\approx {\underline {I}}}$ und ${\displaystyle {\underline {I}}_{L_{p}}=-\mathrm {j} I_{L_{p}}\approx -\mathrm {j} Q{\underline {I}}}$

${\displaystyle {\underline {I}}_{L}\approx {\underline {I}}-\mathrm {j} I_{L_{p}}\approx {\underline {I}}\,(1-\mathrm {j} Q)}$ ${\displaystyle \quad \Rightarrow \quad }$ ${\displaystyle I_{L}\approx I{\sqrt {1+Q^{2}}}\approx QI=I_{L_{p}}}$

wobei benutzt wurde, dass für die Kreisgüte ${\displaystyle Q\gg 1}$ gilt (wegen schwacher Dämpfung).

Hieran liest man unmittelbar ab, dass die Effektivwerte der einzelnen Zweigströme durch Spule und Kondensator den Effektivwert des Klemmenstroms ${\displaystyle I}$ nahe der Resonanzfrequenz bei schwacher Dämpfung überragen. Dieses Verhalten nennt man Stromüberhöhung (vgl. Abb. 13).

Ferner sieht man, dass die Stromüberhöhung ${\displaystyle I_{L}/I=I_{C}/I}$ durch die Kreisgüte ${\displaystyle Q}$ ausdrückbar ist. Bei schwacher Dämpfung, d. h. für ${\displaystyle R_{L}\ll 2{\sqrt {L/C}}}$, gilt nahe der Resonanzfrequenz

${\displaystyle I_{L}/I=I_{C}/I\approx Q={\frac {1}{R_{L}}}{\sqrt {\frac {L}{C}}}}$

Im Gegensatz zum Reihenkreis wird hier aus der Näherung auch im Resonanzfall keine exakte Gleichheit, da die Resonanzfrequenz für den Parallelkreis i. Allg. von der Dämpfung, d. h. vom Verlustwiderstand ${\displaystyle R_{L}}$, abhängt. Man kann aber zeigen, dass im Resonanzfall für den Fehler ${\displaystyle {\mathcal {O}}(R_{L}^{2}C/L)={\mathcal {O}}(Q^{-2})}$ gilt (vgl. Landau-Symbole) und die Näherung sich daher mit quadratischer Geschwindigkeit verbessert, wenn man die Dämpfung abschwächt bzw. die Güte erhöht.

Bei Spannungseinspeisung hängen die Zweigströme ${\displaystyle I_{L}=I_{C}\approx {\sqrt {\frac {C}{L}}}\,U}$ nahe der Resonanzfrequenz bei schwacher Dämpfung nicht (!) vom Verlustwiderstand ${\displaystyle R_{L}}$ ab, die Höhe des Klemmenstroms ${\displaystyle I\approx {\frac {R_{L}C}{L}}\,U}$ jedoch schon. In dem Fall äußert sich die Stromüberhöhung ${\displaystyle I_{L}/I=I_{C}/I}$ bei Verringerung von ${\displaystyle R_{L}}$ nicht im Ansteigen der Zweigströme, sondern im Sinken des Klemmenstroms; insbesondere strebt für ${\displaystyle R_{L}\rightarrow 0}$ auch ${\displaystyle I\rightarrow 0}$. Dieses Verhalten nutzt man z. B. in Sperrkreisen.

Abb. 14 Ortskurve für Parallelkreis für ${\displaystyle R_{L}=1\,\Omega }$, ${\displaystyle L=1\,{\text{H}}}$, ${\displaystyle C=0{,}2\,{\text{F}}}$

Ortskurve für den Parallelkreis

Abb. 15 Vergrößerter Ausschnitt der Ortskurve aus Abb. 14 nahe Koordinatenursprung

Das Verhalten des Parallelkreises bei Veränderung der von außen aufgeprägten Netzfrequenz ${\displaystyle \omega }$ wird durch das Verhalten der Admittanz ${\displaystyle {\underline {Y}}_{p}=G_{p}+\mathrm {j} B_{p}}$ charakterisiert. Graphisch kann das Admittanzverhalten durch eine Ortskurve (vgl. Abb. 14 und Abb. 15) dargestellt werden.

1. Bei Resonanz (d. h. ${\displaystyle \omega =\omega _{r}}$) ist ${\displaystyle B_{p}=0}$, sodass der Zeiger auf der reellen Achse liegt. Die Admittanz stimmt dann mit dem Resonanzleitwert ${\displaystyle G_{pr}}$ überein.
2. Unterhalb der Resonanzfrequenz verhält sich der Blindanteil induktiv, ${\displaystyle B_{p}<0}$, der Zeiger liegt dann unterhalb der reellen Achse;
   oberhalb der Resonanzfrequenz verhält sich der Blindanteil kapazitiv, ${\displaystyle B_{p}>0}$, der Zeiger liegt dann oberhalb der reellen Achse.
3. Die Frequenz ${\displaystyle \omega _{\text{min}}}$, bei der das Minimum des Scheinleitwerts ${\displaystyle Y_{p}(\omega _{\text{min}})=Y_{p,{\text{min}}}}$ angenommen wird, erfüllt ${\displaystyle \omega _{r}\leq \omega _{\text{min}}\leq \omega _{0}}$.
   In Abb. 15 sieht man das daran, dass der Zeiger ${\displaystyle {\underline {Y}}_{p}(\omega _{\text{min}})}$ oberhalb von ${\displaystyle {\underline {Y}}_{p}(\omega _{r})=G_{pr}}$, aber unterhalb von ${\displaystyle {\underline {Y}}_{p}(\omega _{0})}$liegt.
   Für ${\displaystyle R_{L}\neq 0}$ unterscheiden sich die Frequenzen, d. h. ${\displaystyle \omega _{r}<\omega _{\text{min}}<\omega _{0}}$; allerdings liegt ${\displaystyle \omega _{\text{min}}}$ i. d. R. sehr nahe bei ${\displaystyle \omega _{0}}$; im Beispiel ist ${\displaystyle \omega _{\text{min}}/\omega _{0}\approx 99{,}15\%}$, also eine Abweichung von weniger als 1 %. Im Grenzfall ${\displaystyle R_{L}=0}$ tritt Gleichheit ein, d. h. ${\displaystyle \omega _{r}=\omega _{\text{min}}=\omega _{0}}$; dann fallen auch die Zeiger mit dem Resonanzleitwert zusammen, d. h. ${\displaystyle {\underline {Y}}_{p}(\omega _{\text{min}})={\underline {Y}}_{p}(\omega _{0})={\underline {Y}}_{p}(\omega _{r})=G_{pr}}$, denn die Ortskurve liegt dann auf der imaginären Achse.
4. Für ${\displaystyle R_{L}\neq 0}$ ist der Wirkanteil der Admittanz ${\displaystyle \operatorname {Re} {\underline {Y}}_{p}=G_{p}}$ frequenzabhängig. Anschaulich bedeutet dies, dass die Ortskurve keine zur imaginären Achse parallele Gerade sein kann. Umgekehrt hängt daher die Resonanzfrequenz ${\displaystyle \omega _{r}}$ (über den Resonanzleitwert ${\displaystyle G_{pr}}$) vom Verlustwiderstand ${\displaystyle R_{L}}$ ab (d. h. von der Dämpfung ${\displaystyle \delta _{r}}$) – im Gegensatz zum Reihenkreis (!). Im Grenzfall ${\displaystyle R_{L}=0}$ entfällt die Frequenzabhängigkeit, weil dann ${\displaystyle G_{p}=0}$ ist und die Ortskurve auf der imaginären Achse liegt.

Alternativ kann das Verhalten direkt aus ${\displaystyle (*{\scriptstyle {\text{P}}})}$, ${\displaystyle ({\text{RF}})}$ und ${\displaystyle ({\text{TF}})}$ abgelesen werden. Für den 3. Punkt muss man jedoch die Minimalstelle des Scheinleitwerts berechnen (Kurvendiskussion).

Hinweis: Die Admittanz ${\displaystyle {\underline {Y}}_{p}=(R_{L}+\mathrm {j} \omega L)^{-1}+\mathrm {j} \omega C}$ für das Reihenersatzschaltbild (vgl. Abb. 11 links) ist äquivalent zum in Abb. 15 angegebenen Ausdruck; letzterer ergibt sich aus ersterem durch komplex-konjugierte Erweiterung und anschließendes Sortieren nach Real- und Imaginärteil, so erhält man auch die Transformationsformeln ${\displaystyle ({\text{TF}})}$.

Energiebilanz für den Parallelkreis

Wie beim Reihenkreis muss die Gesamtenergie des Parallelkreises im stationären Zustand konstant sein, d. h. ${\displaystyle E=E_{C}+E_{L}={\text{const.}}}$ Duale Ersetzung in der Energiebilanz zum Reihenkreis liefert

${\displaystyle 0={\frac {dE}{dt}}=ui-G_{p}u^{2}\quad \Leftrightarrow \quad ui=G_{p}u^{2}}$

Die Diskussion von ungedämpftem Fall (${\displaystyle G_{p}=0}$ bzw. ${\displaystyle R_{L}=0}$) und gedämpftem Fall (${\displaystyle G_{p}\neq 0}$ bzw. ${\displaystyle R_{L}\neq 0}$) erfolgt analog zum Reihenschwingkreis (vgl. Energiebilanz für den Reihenkreis). Mit Gesamtenergie ${\displaystyle E=CU^{2}}$, ohmscher Verlustleistung ${\displaystyle P_{V}=G_{p}{\overline {u^{2}}}=G_{p}U^{2}}$ und der Resonanzfrequenz ${\displaystyle \omega _{r}}$ lässt sich die Kreisgüte mithilfe ihrer Energiedefinition berechnen (siehe unten).

Kreisgüte

→ Hauptartikel: Gütefaktor

Die in realen Schwingkreisen auftretenden Verluste (ohmsche Verluste, dielektrische Verluste, Abstrahlung) führen dazu, dass die Schwingung eines Schwingkreises gedämpft wird. Ganz ohne Dämpfung würde andererseits bei Resonanz die Amplitude über alle Grenzen wachsen. Ein Maß für die Verluste ist der Gütefaktor.

Die Resonanzkurve (vgl. Abb. 8) stellt in einem Diagramm dar, wie weit es in Abhängigkeit von der Erregerfrequenz bei einem gegebenen Gütefaktor zu einer Amplitudenüberhöhung kommt.

Kreisgüte freier Schwingungen

Für den Reihenschwingkreis freier Schwingungen ergibt sich im Fall schwacher Dämpfung mit Dissipationsenergie ${\displaystyle W_{V}={\frac {E}{\tau }}\,T_{0}}$ aus der Energiebilanz oben und der Energiedefinition des Gütefaktors

${\displaystyle Q=2\pi {\frac {E}{W_{V}}}=\omega _{0}\tau =2\pi \,f_{0}\,\tau }$

wobei wegen obiger Voraussetzung ${\displaystyle \omega _{d}\approx \omega _{0}=2\pi f_{0}}$ gilt. Hier ist die Güte also das ${\displaystyle 2\pi }$-fache der Anzahl der Schwingungen bis die Energie auf den Bruchteil ${\displaystyle 1/e}$ gesunken ist (vgl. Abb. 6). Die Formel ist auch für den ungedämpften Idealfall ${\displaystyle R=0}$ anwendbar, die Güte ist dann ${\displaystyle Q=\infty }$.

Ferner erhält man durch Einsetzen von ${\displaystyle \omega _{0}=1/{\sqrt {LC}}}$ und ${\displaystyle \tau =L/R}$ die alternative Formel

${\displaystyle Q=\omega _{0}\tau ={\frac {1}{R}}{\sqrt {\frac {L}{C}}}}$

Im Fall schwacher oder ohne Dämpfung stimmen also die Güten für Reihenschwingkreise freier und erzwungener Schwingungen überein (vgl. unten).

Kreisgüte erzwungener Schwingungen

Reihenkreis: Mit Verlustleistung ${\displaystyle P_{V}=RI^{2}}$ aus der Energiebilanz für den Reihenkreis, gespeicherter Energie ${\displaystyle E=LI^{2}}$, Resonanzfrequenz ${\displaystyle \omega _{r}=\omega _{0}=1/{\sqrt {LC}}}$ und der Energiedefinition des Gütefaktors ergibt sich

${\displaystyle Q=\omega _{0}\,{\frac {E}{P_{V}}}={\frac {1}{\sqrt {LC}}}{\frac {L}{R}}={\frac {1}{R}}{\sqrt {\frac {L}{C}}}}$

Parallelkreis: Für Parallelkreis bei schwacher Dämpfung, d. h. ${\displaystyle \delta _{r}\ll \omega _{0}}$ (mit ${\displaystyle \delta _{r}=R_{L}/2L}$), gilt für die Resonanzfrequenz ${\displaystyle \omega _{r}\approx \omega _{0}={\sqrt {1/LC}}}$. Im Resonanzfall lautet die Verlustleistung aus der Energiebilanz ${\displaystyle P_{V}=G_{pr}U^{2}}$, wobei ${\displaystyle G_{pr}=R_{L}C/L}$ der Resonanzleitwert ist (Kehrwert ${\displaystyle R_{pr}=1/G_{pr}}$ heißt Resonanzwiderstand). Mit der gespeicherten Energie ${\displaystyle E=CU^{2}}$ und der Energiedefinition des Gütefaktors folgt

${\displaystyle Q=\omega _{r}\,{\frac {E}{P_{V}}}\approx {\frac {1}{\sqrt {LC}}}{\frac {C}{G_{pr}}}={\frac {1}{G_{pr}}}{\sqrt {\frac {C}{L}}}={\frac {1}{R}}_{L}{\sqrt {\frac {L}{C}}}}$

Auch im verlustfreien Grenzfall sind die Formeln noch anwendbar, für ${\displaystyle R,R_{L}\rightarrow 0}$ im Reihen- bzw. Parallelkreis strebt ${\displaystyle Q\rightarrow \infty }$.

Oszillator

Einmal angestoßen und dann sich selbst überlassen, schwingt ein Schwingkreis in der Nähe seiner Resonanzfrequenz f₀. Infolge der Dämpfung durch Verluste nimmt die Amplitude der Schwingung im Laufe der Zeit ab („gedämpfte Schwingung“), wenn nicht durch eine aktive Verstärkerschaltung (beispielsweise mit einem Transistor) oder einem negativen differentiellen Widerstand regelmäßig wieder Energie zugeführt wird. Man spricht dann auch von einer Mitkopplung oder von einer Entdämpfung des Schwingkreises. Eine solche Schaltung bildet eine Oszillatorschaltung (Schwingungserzeuger), ein Beispiel ist die Meißner-Schaltung.

Phasenverschiebung

Abb. 16 Messschaltung der Phasenverschiebung bei Resonanz

Abb. 17 Phasenverschiebung am Schwingkreis bei geringer und starker Dämpfung

Wird ein Schwingkreis durch einen externen Oszillator und schwache induktive Kopplung (vgl. Abb. 16) zu erzwungenen Schwingungen angeregt, reagiert er mit einer Phasenverschiebung zwischen 0° bei extrem tiefen Frequenzen und 180° bei sehr hohen Frequenzen (vgl. Abb. 17). Bei Resonanz beträgt die Phasenverschiebung genau 90°.

In der Umgebung der Resonanzfrequenz ist die Abweichung der Phasenverschiebung φ von 90° fast proportional zur Abweichung der Frequenz f. Das wird bei Demodulationsschaltungen von Frequenzmodulation ausgenutzt.

${\displaystyle \varphi -90^{\circ }=k\cdot (f-f_{0})}$

Der Proportionalitätsfaktor k ist umso größer, je kleiner die Dämpfung des Schwingkreises ist. Diese lässt sich durch den Reihenwiderstand zur Induktivität ändern. Bei verschwindender Dämpfung hätte die Kurve die Form einer Heaviside-Funktion.

Abstimmung

Unter Abstimmung versteht man das Einstellen der Resonanzfrequenz auf einen gewünschten Wert. Für den Reihenkreis hängt die Resonanzfrequenz nur von der L und C ab, auch für den schwach gedämpften Parallelkreis gilt näherungsweise ${\displaystyle \omega _{r}\approx 1/{\sqrt {LC}}}$. Indem man L und C passend wählt, kann der gewünschte Wert eingestellt und der Schwingkreis entsprechend den Erfordernissen abgestimmt werden (etwa beim Sperrkreis, um bestimmte Frequenzen zu sperren).

Die Induktivität L wird durch die Geometrie und das Füllmaterial (Spulenkern) der Spule bestimmt. Je kürzer die Spule und je höher ihre Wicklungszahl, desto höher die Induktivität. Ferner, je leichter der Spulenkern in Richtung des äußeren Magnetfeldes (= Feld der Spule) magnetisierbar, desto höher die Induktivität. Weichmagnetische Kerne (z. B. Weicheisen, Nickel-Eisen-Legierungen) erhöhen die Induktivität gegenüber der Luftspule (Luft als Kern), weil sie die magnetische Flussdichte im Spuleninneren erhöhen. Bei diamagnetische Kernen (z. B. Bismut, Silber, Supraleiter) ist es umgekehrt, weil die Magnetisierung in Gegenrichtung zum äußeren Magnetfeld erfolgt. Eine Liste mit Materialien verschiedener Magnetisierbarkeiten findet sich unter Permeabilitätszahl ${\displaystyle \mu _{r}}$ (= Maß für die Magnetisierbarkeit).

Die Kapazität C wird ebenfalls durch die Geometrie und das Füllmaterial (Dielektrikum) bestimmt. Im einfachsten Fall eines Plattenkondensators ist die Kapazität desto höher, je geringer der Plattenabstand und je größer die Platten. Ferner, je leichter das Dielektrikum elektrisch polarisierbar, desto höher die Kapazität. Dielektrika können die Kapazität gegenüber dem Vakuumkondensator (Vakuum als Dielektrikum) nur erhöhen, aber nicht verringern. Das liegt daran, dass das Vakuum keine Ladungsträger enthält und somit nicht polarisationsfähig ist. Eine Liste mit Dielektrika verschiedener Polarisierbarkeiten findet sich unter Permittivitätszahl ${\displaystyle \varepsilon _{r}}$ (= Maß für die elektrische Polarisierbarkeit).

Anwendung

Filter

Der Scheinwiderstand ist frequenzabhängig, in der Umgebung der Resonanzfrequenz wird er beim Reihenschwingkreis minimal und beim Parallelschwingkreis maximal. Diese Frequenzabhängigkeit ermöglicht, aus einem Signalgemisch unterschiedlicher Frequenzen eine bestimmte Frequenz herauszufiltern – entweder um sie allein durchzulassen, oder um sie gezielt zu unterdrücken. Der Parallelschwingkreis hat zudem den Vorteil, Gleichstrom wie beispielsweise den Betriebsstrom des Transistors unbehindert passieren zu lassen. Deshalb wird beim Einsatz in einem selektiven Verstärker immer ein Parallelschwingkreis verwendet.

• Bei älteren Telefonanlagen wurden über die Zweidrahtleitung sowohl Sprache als auch – auf höherer Frequenz – die Gebührenimpulse gesendet. Im Telefonapparat war ein Sperrkreis (Parallelschwingkreis als Zweipol) eingebaut, um die Frequenz des Impulses für den Hörer zu unterdrücken. Nur diese wurde über einen Reihenschwingkreis zum Gebührenzähler geschickt, vor dem wiederum die Sprachfrequenzen gesperrt wurden.
• Mit Parallelschwingkreisen werden Rundfunkempfänger auf den gewünschten Sender abgestimmt. Ein Schwingkreis wird zwischen die Eingangspole geschaltet – im einfachsten Fall des Detektorempfängers direkt zwischen Antenne und Erde. Das Ausgangssignal wird an diesen Anschlüssen abgenommen und der weiteren Verarbeitung (Mischung bei einem Überlagerungsempfänger, Demodulation) zugeführt.
• Die Endstufen von Sendeanlagen erzeugen häufig unerwünschte Oberschwingungen, die nicht über die Antenne abgestrahlt werden dürfen und durch einige Schwingkreise nach der Endstufe unterdrückt werden müssen. Wird der Schwingkreis durch einen Resonanztransformator ersetzt, kann so auch eine Leitungsanpassung an die Impedanz des Antennenkabels erfolgen.
• Mit Saugkreisen können störende Frequenzen einem Signalgemisch ausgefiltert (kurzgeschlossen) werden. Dazu wird er vor den eigentlichen Empfänger zwischen Antenne und Erde angeschlossen. Bei einfachen Rundfunkempfängern kann so ein sehr starker Ortssender ausgefiltert werden, um die eigentlichen Frequenzselektionsstufen dann auf die gewünschte Frequenz eines weiter entfernteren und dadurch schwächer einfallenden Senders abzustimmen, die sonst vom Ortssender überlagert würden. Gut geeignet und öfter eingesetzt ist auch ein Sperrkreis in der Antennenzuleitung.

Parallel- und Reihenschwingkreise können je nach Beschaltung auch die jeweils andere Aufgabe übernehmen. So kann ein lose gekoppelter Parallelschwingkreis Energie ausschließlich bei seiner Eigenfrequenz aufnehmen (Saugkreis); ein Reihenschwingkreis in Reihe in einer Signalleitung lässt nur Frequenzen seiner Eigenresonanz passieren. Dagegen lässt ein in eine Signalleitung in Reihe geschalteter Parallelschwingkreis genau seine Eigenfrequenz nicht passieren – vorausgesetzt, er wird durch diese nicht maßgeblich bedämpft.

Kompensation von Blindstrom

Verbraucher im elektrischen Energieversorgungsnetz beziehen elektrische Energie und geben sie z. B. als thermische, mechanische, chemische Energie weiter. Vielfach speichern sie auch Energie, z. B. in Motoren als magnetische Feldenergie. Das Feld wird im Rhythmus der Netzwechselspannung auf- und wieder abgebaut, und die Energie wird bezogen und zurückgeliefert. Diese Energiependelung erzeugt Blindstrom, der Quelle und Netz belastet und vermieden werden soll. Dazu wird ein Schwingkreis aufgebaut: Einer Induktivität wird eine Kapazität parallelgeschaltet – oder umgekehrt. Das Zusatzbauteil wird so dimensioniert, dass die Resonanzfrequenz gleich der Netzfrequenz wird und dadurch ein möglichst hoher Scheinwiderstand entsteht. Diese Schaltungsmaßnahme wird Blindstromkompensation genannt.

Schwingkreise als Ersatzschaltbilder

Neben Schwingkreisen gibt es viele weitere elektronische Konstruktionen, die in Anwendungen an Stelle von Schwingkreisen eingesetzt werden (besonders bei sehr hohen Frequenzen). Siehe hierzu Lecherleitung, Topfkreis, Hohlraumresonator, aber auch Antennendipol. Die physikalische Funktion dieser Konstruktionen basiert meist auf der Nutzung von stehenden Wellen und unterscheidet sich damit grundsätzlich von der physikalischen Funktion eines Schwingkreises. Für derartige Konstruktionen werden häufig Ersatzschaltbilder in Form elektrischer Schwingkreise angegeben, die eine vereinfachte, angenäherte Berechnung ihres Verhaltens erlauben.

Ersatzschaltbilder mit ihren idealen elektronischen Bauelementen bilden das Verhalten der „ersetzten“ Konstruktion nach, nicht jedoch ihren technischen Aufbau oder ihre Wirkungsweise.

Messgerät

Die Resonanzfrequenz von Schwingkreisen im MHz-Bereich kann mit einem Dipmeter gemessen werden.

Literatur

• Hans-Peter Beck et al.: Das Ingenieurwissen Elektrotechnik. Springer Vieweg, Berlin 2014, ISBN 978-3-662-44031-5.
• Wolfgang Demtröder: Experimentalphysik 2. Springer-Verlag, Berlin 2006, ISBN 3-540-33794-6.
• Thomas Harriehausen, Dieter Schwarzenau: Moeller Grundlage der Elektrotechnik. Springer Vieweg, Wiesbaden 2020, ISBN 978-3-658-27839-7.
• Ralf Kories und Heinz Schmidt-Walter: Taschenbuch der Elektrotechnik. Verlag Harri Deutsch, Frankfurt a. M. und Thun.
• Klaus Lunze: Theorie der Wechselstromschaltungen. Verlag Technik, Berlin 1991, ISBN 3-341-00984-1.
• Marlene Marinescu, Nicolae Marinescu: Elektrotechnik für Studium und Praxis. Springer Vieweg, Wiesbaden 2020, ISBN 978-3-658-28883-9.
• Wolfgang Pfeiler: Experimentalphysik Band 3. Gruyter Verlag, Berlin/Boston 2017, ISBN 978-3-11-044557-2.
• Martin Gerhard Wegener: Moderne Rundfunk-Empfangstechnik. Franzis-Verlag, München 1985, ISBN 3-7723-7911-7.
• Wilfried Weißgerber: Elektrotechnik für Ingenieure 2. Vieweg/Teubner, Wiesbaden 2009, ISBN 978-3-8348-0474-7.

Weblinks

Commons: Schwingkreis – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Schwingkreis – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

• HTML5-App zur Demonstration eines Schwingkreises