In der Mathematik ist das Hölder-Mittel, der Höldersche Mittelwert (nach Otto Hölder, 1859–1937) oder das Potenzmittel (engl. u. a. (p-th) power mean) ein (manchmal auch der) verallgemeinerter Mittelwert. Die Bezeichnung ist uneinheitlich, Bezeichnungen wie das -te Mittel, Mittel der Ordnung oder vom Grad oder mit Exponent sind auch im Umlauf. Im Englischen wird es auch als generalized mean bezeichnet.
Ebenso uneinheitlich sind die Schreibweisen, statt wird auch , oder geschrieben.
Das Hölder-Mittel verallgemeinert die seit den Pythagoreern bekannten Mittelwerte wie das arithmetische, geometrische, quadratische und harmonische Mittel durch Einführung eines Parameters
Definition
Für eine reelle Zahl wird das Hölder-Mittel der Zahlen zur Stufe definiert als
- ,
wobei die Wurzelschreibweise üblicherweise nur für natürliche Zahlen verwendet wird.
Eine dazu passende Definition für ist
Eigenschaften
- Das Hölder-Mittel ist homogen bezüglich , das heißt
- Außerdem gilt
- Eine wichtige Ungleichung zu den Hölder-Mitteln ist
- Daraus folgt etwa (Spezialfälle) die Ungleichung der Mittelwerte
- Die Potenzmittelwerte stehen mit den Stichprobenmomenten um Null recht einfach in Beziehung:
- In der Stochastik wird die Konvergenz im p-ten Mittel über diese Potenzmittelwerte definiert.
Spezialfälle
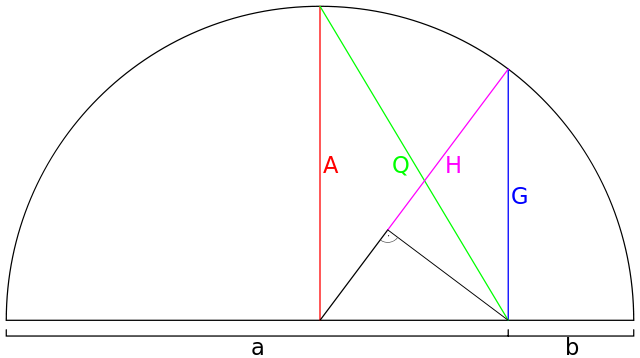
H = Harmonisches Mittel, G = Geometrisches Mittel,
A = Arithmetisches Mittel, Q = Quadratisches Mittel
Mittels Wahl eines geeigneten Parameters ergeben sich die bekannten Mittelwerte:
| Minimum | ||||
| Harmonisches Mittel | ||||
| Geometrisches Mittel | ||||
| Arithmetisches Mittel | ||||
| Quadratisches Mittel | ||||
| Kubisches Mittel | ||||
| Maximum |
Weitere Verallgemeinerungen
Zusammenfassung
Kontext
Gewichtetes Hölder-Mittel
Auch zu dem Hölder-Mittel lässt sich ein gewichtetes Mittel definieren: Das gewichtete Hölder-Mittel lässt sich mit den Gewichten mit definieren als
wobei für das ungewichtete Hölder-Mittel verwendet wird.
f-Mittel
- Vergleiche Quasi-arithmetisches Mittel
Das Hölder-Mittel lässt sich weiter verallgemeinern zu
bzw. gewichtet zu
Dabei ist eine Funktion von ; das Hölder-Mittel verwendet .
Weitere Beispiele:
- Sind die Renditen einer Kapitalanlage in den Jahren bis , so erhält man die mittlere Rendite als -Mittel der einzelnen Renditen zur Funktion .
- Sind die Alter von Personen, so erhält man das versicherungstechnische Durchschnittsalter als -Mittel der einzelnen Alter zur Funktion ; dabei bedeutet die Sterbeintensität. In der Praxis ist das summengewichtete versicherungstechnische Durchschnittsalter relevant, hier werden die Alter der versicherten Personen mit den jeweiligen Versicherungssummen gewichtet; die Sterbeintensität wird oft durch die einjährige Sterbewahrscheinlichkeit ersetzt.
Siehe auch
Literatur
- Julian Havil: Gamma: Eulers Konstante, Primzahlstrände und die Riemannsche Vermutung, Springer, Berlin 2007, ISBN 978-3-540-48495-0
- P. S. Bullen: Handbook of Means and Their Inequalities. Dordrecht, Netherlands: Kluwer, 2003, S. 175–265
Weblinks
- Eric W. Weisstein: Power mean. In: MathWorld (englisch).
- Weighted Power Mean und Proof auf planetmath.org (engl.)
- Examples of Generalized Mean
- Juttas Mathe-Newsletter
Wikiwand - on
Seamless Wikipedia browsing. On steroids.








![{\displaystyle M_{p}(x_{1},\dots ,x_{n})=\left({\frac {1}{n}}\cdot \sum _{i=1}^{n}x_{i}^{p}\right)^{1/p}={\sqrt[{p}]{\frac {x_{1}^{p}+x_{2}^{p}+\ldots +x_{n}^{p}}{n}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/d186559fab5110502802e5e21127c7d3a4f371e7)








![{\displaystyle {\bar {x}}(p)={\sqrt[{p}]{m_{p}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/34cc4385c2739912f9cc12d2cafcf42fea7c7ebc)







![{\displaystyle ={\sqrt[{n}]{x_{1}\cdot \dots \cdot x_{n}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/dd317441f730ad5aff3e01e05c62ae0faf400ba1)








![{\displaystyle ={\sqrt[{3}]{\frac {x_{1}^{3}+\dots +x_{n}^{3}}{n}}}}](http://wikimedia.org/api/rest_v1/media/math/render/svg/1f692aa3f6af6180bfae135a227100bc0c56f11a)

















