Primtal

Et primtal er et positivt heltal større end 1, der ikke er deleligt med andre hele positive tal end 1 og tallet selv, kaldet de trivielle divisorer. Ethvert positivt heltal (større end 1) kan skrives som et produkt af primtal på entydig vis (når der ses bort fra rækkefølgen af primtallene). En sådan opskrivning kaldes tallets primfaktoropløsning, og de indgående primtal kaldes tallets primfaktorer. F.eks. er 60 = 2² × 3 × 5. Det faktum, at ethvert positivt helt tal (større end 1) entydigt kan skrives som et produkt af primfaktorer, kaldes aritmetikkens fundamentalsætning.

Det højest kendte primtal efter år

Bemærk, at 1 ikke er et primtal i definitionen ovenfor, da der jo netop af et primtal kræves, at det er større end 1. Man kunne godt have defineret 1 til at være et primtal, men det gør den videre udvikling af teorien mere besværlig, idet mange sætninger kun gælder for primtal større end eller lig 2. Det gælder for eksempel for den tidligere oplyste entydighed af primfaktoropløsninger. Hvis 1 var defineret til at være et primtal, ville fx 60 kunne skrives som et produkt af primtal på uendelig mange måder. Derfor er det naturligt at definere 1 til ikke at være et primtal.

Primtal studeres indenfor talteori og danner basis for mange krypteringsalgoritmer.

Hvor mange primtal

Euklid beviste ca. 300 f.kr., at der findes uendeligt mange primtal. Beviset anføres ofte at være et modstridsbevis, idet man antager at man kender alle primtal. Ganger man alle disse tal sammen og lægger en til, får man et tal, der enten er et ikke-kendt primtal, eller som har en ikke kendt primfaktor (idet ingen af dem man kender jo kan gå op). Men faktisk gik hans bevisførelse ud på at hvis man har en hvilken som helst mængde af primtal, kan man altid finde mindst ét primtal til - fremgangsmåden svarer til ovenstående. Og dette kan selvfølgelig gentages i det uendelige.

Flere matematikere har lavet andre beviser for, at der er uendelig mange primtal, specielt har Euler vist, at summen af primtallenes reciprokke værdier ikke konvergerer, men går mod uendelig.

Primtallenes fordeling

Mens det er let at indse, at der findes uendeligt mange primtal, er det straks langt sværere at få styr på, hvordan primtallene fordeler sig. Hvis man betragter en liste over primtal (som den ovenfor), ser det ud til at være ganske "tilfældigt" og usystematisk, hvornår det næste primtal vil dukke op. Men selvom fordelingen af primtallene er uregelmæssig på lille skala, dukker der en fornem regelmæssighed op, når man betragter antallet af primtal i store områder.

antal primtal under 1.000:	168	(16,8 %)
antal primtal under 1.000.000:	78.498	(7,8 %)
antal primtal under 1.000.000.000:	50.847.534	(5,1 %)
antal primtal under 1.000.000.000.000:	37.607.912.018	(3,8 %)
antal primtal under 1.000.000.000.000.000:	29.844.570.422.669	(3,0 %)
antal primtal under 1.000.000.000.000.000.000:	24.739.954.287.740.860	(2,5 %)
antal primtal under 1.000.000.000.000.000.000.000:	21.127.269.486.018.731.928	(2,1 %)

Primtalssætningen (bevíst i 1896) giver en præcis beskrivelse af denne regelmæssighed. Antallet af primtal mindre end ${\displaystyle x}$ kan approksimeres med ${\displaystyle x/(\log x)}$, og den relative fejl ved denne approksimation bliver forsvindende når ${\displaystyle x}$ går mod uendelig. (Her betegner ${\displaystyle \log }$ den naturlige logaritme.)

Det er stadig uafklaret, hvor store udsving fra systematikken fra primtalssætningen, der forekommer. Hvis Riemann-hypotesen er sand, er primtallenes fordeling populært sagt så ensartet, som det er teoretisk muligt. Hvis Riemann-hypotesen mod forventning skulle vise sig at være falsk, ville der derimod igennem hele talrækken være forholdsvis store "bump", hvor tætheden af primtallene afveg mere fra den ideelle end den "behøvede".

Carl Friedrich Gauss forudsagde allerede som 14-årig, i 1791, en formel der angiver omtrentligt hvordan antallet af primtal skulle aftage. Lidt senere mente matematikere, at Gauss' formel overvurderede virkeligheden. Dog opdagede G.H. Hardys assistent ved Cambridge, J.E. Littlewood, i 1914, at Gauss' formel modsat tidligere matematiske synspunkter undervurderede virkeligheden. I 1955 demonstrerede Stanley Skewes, at undervurderingen begynder omkring tallet 10^{1010.000.000.000.000.000.000.000.000.000.000.000}, "Skewes' tal", hvilket betragtes som det største tal der nogensinde er blevet anvendt til matematiske formål.^[1]

Liste over primtal

Primtallene op til 1000 er:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991 og 997.

Største kendte primtal

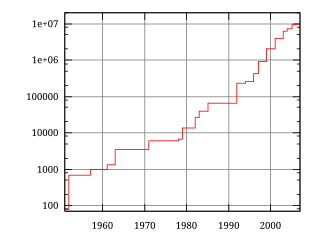
Med fremkomsten af computere er der sket en kraftig udvikling i det største kendte primtal. Det største kendte primtal har næsten altid været af formen 2ⁿ-1, som kaldes mersennetal (bemærk at ikke alle tal på denne form er primtal!). I 2024 var det største kendte primtal 2^136.279.841-1, det blev fundet den 21. oktober 2024 af GIMPS, som er en internetgruppe, der benytter overskydende computertid til at finde mersenneprimtal. Dette tal er på 41.024.320 decimale cifre.

Primtal på over 1.000 cifre kaldes et titanprimtal og en person der har fundet et sådan kaldes en "titan".

Forskellige grupper af primtal

Alt efter egenskaber kan primtal kategoriseres i grupper, f.eks.:

• Primtalstvillinger, det vil sige to primtal der ligger så tæt på hinanden som muligt (bortset fra eksemplet med 2 og 3 vil det sige at der er adskilt af to, f.eks. 5 og 7 eller 17 og 19).
• Primtalstrillinger, tre primtal der ligger så tæt på hinanden som muligt (f.eks. 5, 7, 11)
• Primtalsfirlinger, fire primtal der ligger så tæt på hinanden som muligt (f.eks. 5, 7, 11, 13)
• Mersenneprimtal, primtal på formen ${\displaystyle 2^{n}-1}$
• Fermatprimtal, primtal på formen ${\displaystyle 2^{2^{n}}+1}$
• Pythagoræiske primtal, primtal på formen 4n + 1
• Fakultetsprimtal, primtal på formen ${\displaystyle n!\pm 1}$
• Sexede primtal, to primtal hvor forskellen mellem dem er 6
• Titanprimtal, primtal med mindst 1000 cifre
• Gigantprimtal, primtal med mindst 10.000 cifre
• Megaprimtal, primtal med mindst 1.000.000 cifre
• Cirkulære primtal, primtal hvor hver cyklisk permutation (base 10) vil være et primtal (eksempelvis 1193)
• Palindromprimtal, primtal som er ens uanset om de læses forfra eller bagfra (eksempelvis 101)
• Latmirp et primtal der også er et primtal, hvis rækkefølgen på cifrene vendes om. (eksempelvis 13)

Af mere underholdende karakter er de såkaldte "James Bond primtal", der er primtal der ender med 007. De fire første er 7 (007), 4007, 6007 og 9007.^[2][3]

Ubesvarede spørgsmål

• Ovennævnte Riemann-hypotese opfattes af de fleste som det vigtigste ubesvarede spørgsmål i matematikken.
• Det vides ikke, om der findes uendelig mange primtalstvillinger. I 2013 beviste Zhang Yitang, at der findes uendeligt mange "par" af primtal, hvor forskellen mellem de to primtal er mindre end ${\displaystyle 7\cdot 10^{7}}$.
• Goldbachs formodning siger, at ethvert lige heltal større end 2 kan skrives som summen af to primtal. Man har afprøvet denne formodning for meget store tal og har endnu ikke fundet noget modeksempel. Det vides imidlertid ikke om formodningen er sand. Et bevis angående Golbachs Formodning kan have to udfald: "1. Formodningen er sand. 2. Formodningen er falsk.". Hvis formodningen er falsk er man garanteret eksistensen af et bevis herfor.^{[kilde mangler]} Derimod kan formodningen godt være sand men ubeviselig.^{[kilde mangler]} Der kan dog ikke eksistere et bevis for at Goldbachs formodning er uløselig (sådan som det for eksempel er blevet bevist for kontinuumhypotesen), da man heraf ville kunne slutte at formodningen er sand og dermed ikke uløselig.^{[kilde mangler]}

Andre egenskaber

• Ethvert primtal større end 3 har en "nabo" i 6-tabellen (fx er 5 nabo til 6, 11 er nabo til 12 osv.). Dette kan man let vise ved at kigge på den rest et primtal må have ved division med 6. Det er let at se, at resten altid må være 1 eller 5, idet 0, 2 og 4 udelukkes af at 2 ellers ville gå op, mens 3 udelukkes af at 3 ville gå op, hvilket strider mod at tallet er et primtal større end 3.

Dette betyder ikke, at en rest på 1 eller 5 ved division med 6 samtidig er en indikator på, om tallet (dividenden) er et primtal. For eksempel er resten ved division af 25 med 6 lig med 1.

• Med undtagelse for 2 og 5 har alle andre primtal en sidste cifre af 1 (fra tallet 11 og større) , 3, 7 eller 9.

• Følgende serie af primtal er meget intressant:

31, 331, 3 331, 33 331, 333 331, 3 333 331 er alle primtal. Før computernes tid var matematikerne rimelig overbevist om, at den slags tal sandsynligvis altid er primtal. Men beviser manglede for antagelsen af, at serien skulle fortsættes. Man fandt senere ud af, at 33 333 331 også er et primtal. Men så opdagede man, at 333 333 331 ikke er et primtal, da 17 x 19 607 843 = 333 333 331. Det er et godt eksempel på, at man bør bestræbe sig på at bevise matematiske formodninger.

Se også

• Wilsons sætning
• Eratosthenes' si

Eksterne henvisninger

• David Wells, Primtal - Matematikkens gådefulde tal - fra A-Ø, ISBN 978-87-571-2561-0
• En grundig gennemgang på engelsk af primtal Arkiveret 7. juni 2004 hos Wayback Machine
• De 10.000 første primtal

1. Simon Singh, Fermats store sætning, ISBN 87-00-31406-4, side 194.
2. Jens Ramskov, "Primtal: Fakta og Formodninger", Ingeniøren, nummer 47, 24. november 2006.
3. David Wells, Primtal – Matematikkens gådefulde tal fra A-Ø, Nyt Teknisk Forlag, ISBN 87-571-2561-9.