Gofod dau ddimensiwn

Mewn Mathemateg, mae gofod dau ddimensiwn (neu gofod 2-ddimensiwn) yn lleoliad geometrig lle nodir safle rhyw elfen (e.e. pwynt neu groesbwynt) gan ddau werth a elwir yn "baramedrau". Caiff ei gynrychioli'n gyffredin gan y symbol ℝ². Mae gofod dau ddimensiwn, fel yr awgryma'r enw, yn fath o ddimensiwn.

System cyfesurynnau Cartesaidd dau ddimensiwn

Gellir ystytried gofod dau ddimensiwn fel dyluniad o'r bydysawd real ar blân ac fel gofod Ewclidaidd. Gelwir y ddau ddimensiwn yn "hyd" a "lled". Mae'r term "Ewclidaidd"^[1] yn gwahaniaethu'r mannau hyn o fathau eraill a astudir o fewn geometreg fodern ac maent yn ymwneud â'r dimeniynau uwch e.e. mecaneg Lagrangaidd neu Hamiltonaidd.

Hanes

Mae cyfrol I - IV a VI o Elfennau gan Euclid yn ymdrin â geometreg dau ddimensiwn, gan ddatblygu cysyniadau fel tebygrwydd siapiau, Theorem Pythagoras (Gosodiad 47), hafaledd onglau ac arwynebedd, cyfochredd, swm yr onglau mewn triongl, y tri achos lle mae trionglau yn "gyfartal" (sydd â'r un arwynebedd), a nifer o bynciau perthnasol eraill.

Mewn geometreg

Prif: Plân geometrig

Prif: Geometreg Ewclidaidd

System gyfesurynnol

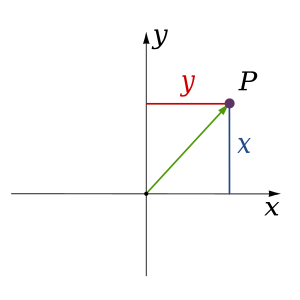
Mewn mathemateg, mae geometreg ddadansoddol (a elwir hefyd yn "geometreg Cartesaidd") yn disgrifio pob pwynt o fewn lle (neu 'ofod') dau ddimensiwn trwy ddefnyddio dau gyfesuryn.

Dylunnir dwy echelin berpendicwlar sy'n croesi ei gilydd ar y tarddiad. Maent fel arfer yn cael eu labelu x ac y. Mae lleoliad pob pwynt o fewn y gofod dau ddimensiwn yn cael ei nodi gan bâr o rifau real, gyda phob rhif yn rhoi pellter y pwynt hwnnw o'r tarddiad a fesurwyd ar hyd yr echelin perthnasol.

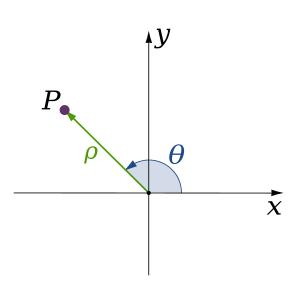
System gyfesurynnol arall a ddefnyddir yn helaeth yw'r system cyfesurynnol polar, sy'n nodi pwynt o ran ei bellter o'r tarddiad a'i ongl o'i gymharu â phelydryn cyfeiriol.

• 
  System cyfesurynnau Cartesaidd
• 
  System cyfesurynnol polar

Gweler hefyd

• Modelu dau ddimensiwn

Cyfeiriadau

1. termau.cymru; Y Termiadur Addysg - Ffiseg a Mathemateg; adalwyd 11 Medi 2018.