Llinell

Mewn mathemateg, cyflwynwyd y syniad o linell neu linell syth gan fathemategwyr ganrifoedd yn ôl i gynrychioli gwrthrychau syth heb fawr o drwch a heb fod yn llinellau crwm. Cynrychiolir gwrthrychau o'r fath gan linell, a wnaed fel arfer, gyda chymorth pren syth, pwrpasol (e.e. y pren mesur). Mae 'llinell' yn enw benywaidd; y lluosog yw 'llinellau'.

Llinell

Enghraifft o:	cysyniad geometregol
Math	algebraic curve, member of a group, locws, llinell, generalised circle, geometric primitive
Rhan o	plân geometraidd
Yn cynnwys	pwynt, orientation, abstract reference point, ray
Ffeiliau perthnasol ar Gomin Wicimedia

Mae gan y llinellau coch a glas yn y graff hwn yr un llethr (graddiant); mae gan y llinellau coch a gwyrdd yr un rhyngdoriad-y (y-intercept) h.y. mae nhw'n croesi'r echelin-y yn yr un lle.

Segment llinell.

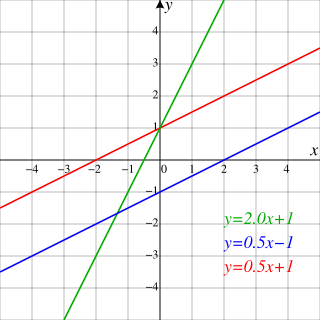
Mewn mathemateg fodern, mae'r cysyniad o linell wedi'i chysylltu'n agos iawn â geometreg. Er enghraifft, mewn geometreg ddadansoddol, mae llinell yn y plân yn aml yn cael ei diffinio fel y set o bwyntiau y mae eu cyfesurynnau'n bodloni hafaliad llinol penodol, ond mewn cyd-destun mwy haniaethol, megis 'geometreg amlder' (incidence geometry), gall llinell fod yn wrthrych annibynnol, ar wahân i'r set o bwyntiau sy'n gorwedd arni.

Hanes

Hyd at 17g, diffiniwyd llinellau yn y modd hwn: "Y linell [syth neu grwm] yw'r enghraifft gyntaf o faint, sydd ag un dimensiwn yn unig, sef hyd, ac heb led na dyfnder iddo, ac nid yw'n ddim byd mwy na phwynt yn llifo neu'n rhedeg..."^[1]

O fewn geometreg Ewclidaidd

Yn y plân Cartesaidd

Gellir disgrifio llinellau mewn plân Cartesaidd neu mewn cyfesurynnau affin (affine) yn nhermau algebra gyda hafaliadau llinol (linear equations).

Mewn dau ddimensiwn, rhoddir yr hafaliad ar gyfer llinellau nad ydynt yn fertigol ar ffurf:

${\displaystyle y=mx+b}$

ble:

m yw oledd neu'n graddiant y linell.

b yw y-intercept y linell.

x yw newidyn annibynnol y ffwythiant y = f(x).

Dynodir goledd neu raddiant y linell drwy bwyntiau ${\displaystyle A(x_{a},y_{a})}$ a ${\displaystyle B(x_{b},y_{b})}$, pan fo ${\displaystyle x_{a}\neq x_{b}}$, yn cael ei roi gan ${\displaystyle m=(y_{b}-y_{a})/(x_{b}-x_{a})}$ a gellr sgwennu'r hafaliad am y linell hon fel ${\displaystyle y=m(x-x_{a})+y_{a}}$.

Yn ${\displaystyle \mathbb {R^{2}} }$, mae pob llinell ${\displaystyle L}$ (gan gynnwys y linell fertigol) yn cael eu disgrifio gan hafaliad llinol ar ffurf

${\displaystyle L=\{(x,y)\mid ax+by=c\}}$

gyda chyfernodau real a sefydlog a, b ac c fel bod a a b ddim yn sero. Drwy ddefnyddio'r dull hwn, mae'r llinellau fertigol yn cyfateb i'r hafaliad b = 0.

Yn y cyfesurynnau pegynlinol

Yn y cyfesurynnau pegynlinol (polar coordinates) ar y plân Ewclidaidd gellir mynegi hafaliad y linell fel:

${\displaystyle r={\frac {mr\cos \theta +b}{\sin \theta }},}$

ble mae m yn oledd y linell, a b yw'r y-intercept. Pan fo θ = 0 yna bydd y graff yn anniffiniedig. Gellir ailysgrifennu'r hafaliad i ddileu'r diffygion yn y modd hwn:

${\displaystyle r\sin \theta =mr\cos \theta +b.}$

Fel hafaliad fector

Gellir mynegi hafaliad fector y linell drwy A a B fel ${\displaystyle \mathbf {r} =\mathbf {OA} +\lambda \,\mathbf {AB} }$ (ble λ yw'r sgalar).

Os mai a yw'r fector OA a b yw'r fector OB, yna, gellir sgwennu hafaliad y linell fel: ${\displaystyle \mathbf {r} =\mathbf {a} +\lambda (\mathbf {b} -\mathbf {a} )}$.

Gellir disgrifio pelydryn ar bwynt A drwy gyfyngu λ. Ceir un pelydryn os yw λ ≥ 0, a'r belydryn cyferbyn os yw λ ≤ 0.