Násobení matic

Součin matic^[1][2] hovorově též maticové násobení (neplést se skalárním násobkem matice) je v matematice zobecnění součinu čísel na matice. Formálně se dá definovat jako binární operace na maticích odpovídajících typů. Využívá se v matematice, fyzice a jejich aplikacích, obvykle pro popis skládání lineárních zobrazení.

Pro součin matic musí být počet sloupců v první matici roven počtu řádků ve druhé matici. Výsledná matice má počet řádků první matice a počet sloupců druhé matice.

Speciálním případem násobení matic je součin matice typu ${\displaystyle m\times n}$ a vektoru braného jako matice o typu ${\displaystyle n\times 1}$ (sloupcový vektor). Tento součin lze interpretovat jako aplikaci lineárního zobrazení reprezentovaného transformační maticí na vektor.

Formální definice

Pokud je ${\displaystyle {\boldsymbol {A}}}$ matice typu ${\displaystyle m\times n}$ a ${\displaystyle {\boldsymbol {B}}}$ je matice typu ${\displaystyle n\times p}$, jejich součin ${\displaystyle {\boldsymbol {A}}\cdot {\boldsymbol {B}}}$ je matice typu ${\displaystyle m\times p}$ definovaná vztahem

${\displaystyle ({\boldsymbol {A}}\cdot {\boldsymbol {B}})_{ij}=\sum _{k=1}^{n}a_{ik}b_{kj}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj}.}$

pro všechny prvky výsledné matice indexované ${\displaystyle i\in \{1,\dots ,m\}}$ a ${\displaystyle j\in \{1,\dots ,p\}}$.

Ve většině případů jsou prvky matice čísla, ale mohou to být jakékoli druhy matematických objektů, pro které je definováno sčítání a násobení, které jsou asociativní a takové, že sčítání je komutativní a násobení je distributivní s ohledem na sčítání, typicky prvky nějakého tělesa. Prvky mohou být dokonce samotné matice (bloková matice).

U reálných matic lze prvek v ${\displaystyle i}$-tém řádku a ${\displaystyle j}$-tém sloupci výsledné matice lze také chápat jako standardní skalární součin vektoru ${\displaystyle i}$-tého řádku první matice s vektorem ${\displaystyle j}$-tého sloupce druhé matice.

Tečka ${\displaystyle \cdot }$ se v součinu vynechává a píše se pouze ${\displaystyle {\boldsymbol {AB}}}$.^[2]

Ukázka výpočtu

Schéma součinu ${\displaystyle {\boldsymbol {A}}{\boldsymbol {B}}}$ dvou matic ${\displaystyle {\boldsymbol {A}}}$ a ${\displaystyle {\boldsymbol {B}}}$.

Součin matic ${\displaystyle {\boldsymbol {A}}={\begin{pmatrix}\color {blue}1&\color {blue}2&\color {blue}3\\\color {orange}4&\color {orange}5&\color {orange}6\\\end{pmatrix}}}$ a ${\displaystyle {\boldsymbol {B}}={\begin{pmatrix}\color {red}1&\color {green}2\\\color {red}3&\color {green}4\\\color {red}5&\color {green}6\\\end{pmatrix}}}$ je

${\displaystyle {\boldsymbol {AB}}={\begin{pmatrix}({\color {blue}1}\cdot {\color {red}1}+{\color {blue}2}\cdot {\color {red}3}+{\color {blue}3}\cdot {\color {red}5})&({\color {blue}1}\cdot {\color {green}2}+{\color {blue}2}\cdot {\color {green}4}+{\color {blue}3}\cdot {\color {green}6})\\({\color {orange}4}\cdot {\color {red}1}+{\color {orange}5}\cdot {\color {red}3}+{\color {orange}6}\cdot {\color {red}5})&({\color {orange}4}\cdot {\color {green}2}+{\color {orange}5}\cdot {\color {green}4}+{\color {orange}6}\cdot {\color {green}6})\\\end{pmatrix}}={\begin{pmatrix}22&28\\49&64\end{pmatrix}}}$

Prvky matice ${\displaystyle {\boldsymbol {A}}}$ zůstávají v řádcích tak, jak jsou, a prvky v matici ${\displaystyle {\boldsymbol {B}}}$ se rozmístí opět do levého a pravého sloupce.

Použití

Historicky bylo násobení matic zavedeno pro usnadnění a objasnění výpočtů v lineární algebře. Tento silný vztah mezi maticovým součinem a lineární algebrou zůstává je fundamentální v celé matematice, stejně jako ve fyzice, chemii, inženýrství a informatice.

Soustavy lineárních rovnic

Obecný tvar soustavy lineárních rovnic je

${\displaystyle {\begin{array}{rcr}a_{11}x_{1}+a_{12}x_{2}+\dots +a_{1n}x_{n}&=&b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\dots +a_{2n}x_{n}&=&b_{2}\\&\vdots &\\a_{m1}x_{1}+a_{m2}x_{2}+\dots +a_{mn}x_{n}&=&b_{m}\\\end{array}}}$

Při použití stejné notace jako výše je zápis soustavy ekvivalentní jednoduché maticové rovnici

${\displaystyle {\boldsymbol {Ax}}={\boldsymbol {b}}}$.

Lineární zobrazení

Pokud má vektorový prostor konečnou bázi, každý z jeho vektorů je jednoznačně reprezentován konečnou posloupností skalárů, nazývanou vektor souřadnic, tvořenou souřadnicemi vektoru vzhledem k bázi. Tyto vektory souřadnic tvoří další vektorový prostor, který je izomorfní původnímu vektorovému prostoru. Vektor souřadnic je běžně zapisován jako sloupcový vektor, což je matice pouze s jedním sloupcem. Sloupcový vektor pak představuje jak souřadnicový vektor, tak i vektor původního vektorového prostoru.

Lineární zobrazení ${\displaystyle A}$ prostoru dimenze ${\displaystyle n}$ do vektorového prostoru dimenze ${\displaystyle m}$ převádí sloupcový vektor

${\displaystyle {\boldsymbol {x}}={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}}$

na sloupcový vektor

${\displaystyle {\boldsymbol {y}}=A({\boldsymbol {x}})={\begin{pmatrix}a_{11}x_{1}+\cdots +a_{1n}x_{n}\\a_{21}x_{1}+\cdots +a_{2n}x_{n}\\\vdots \\a_{m1}x_{1}+\cdots +a_{mn}x_{n}\end{pmatrix}}.}$

Lineární zobrazení ${\displaystyle A}$ je proto definováno maticí

${\displaystyle {\boldsymbol {A}}={\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix}},}$

a zobrazuje sloupcový vektor ${\displaystyle {\boldsymbol {x}}}$ na maticový součin

${\displaystyle {\boldsymbol {y}}={\boldsymbol {Ax}}}$.

Je-li ${\displaystyle B}$ další lineární zobrazení z předchozího vektorového prostoru dimenze ${\displaystyle m}$, do vektorového prostoru dimenze ${\displaystyle p}$, pak jej lze reprezentovat maticí ${\displaystyle {\boldsymbol {B}}}$ řádu ${\displaystyle p\times m}$. Přímý výpočet ukazuje, že matice složeného zobrazení ${\displaystyle B\circ A}$ je rovna součinu ${\displaystyle {\boldsymbol {BA}}}$. Obecný vzorec ${\displaystyle (B\circ A)({\boldsymbol {x}})=B(A({\boldsymbol {x}}))}$, který definuje složené zobrazení, je jedním z specifických případů asociativity maticového součinu:

${\displaystyle ({\boldsymbol {BA}}){\boldsymbol {x}}={\boldsymbol {B}}({\boldsymbol {Ax}})={\boldsymbol {BAx}}.}$

Geometrické rotace

Při použití systému kartézských souřadnic v euklidovské rovině je rotace o úhel ${\displaystyle \alpha }$ kolem počátku (počátek odpovídá nulovému vektoru) lineární zobrazení. Přesněji, $${\displaystyle {\begin{pmatrix}x'\\y'\end{pmatrix}}={\begin{pmatrix}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{pmatrix}}{\begin{pmatrix}x\\y\end{pmatrix}},}$$ kde výchozí bod ${\displaystyle (x,y)}$ i jeho obraz ${\displaystyle (x',y')}$ jsou zapsány jako sloupcové vektory.

Složení rotací o úhel ${\displaystyle \alpha }$ a pak o úhel ${\displaystyle \beta }$ odpovídá maticovému součinu $${\displaystyle {\begin{pmatrix}\cos \beta &-\sin \beta \\\sin \beta &\cos \beta \end{pmatrix}}{\begin{pmatrix}\cos \alpha &-\sin \alpha \\\sin \alpha &\cos \alpha \end{pmatrix}}={\begin{pmatrix}\cos \beta \cos \alpha -\sin \beta \sin \alpha &-\cos \beta \sin \alpha -\sin \beta \cos \alpha \\\sin \beta \cos \alpha +\cos \beta \sin \alpha &-\sin \beta \sin \alpha +\cos \beta \cos \alpha \end{pmatrix}}={\begin{pmatrix}\cos(\alpha +\beta )&-\sin(\alpha +\beta )\\\sin(\alpha +\beta )&\cos(\alpha +\beta )\end{pmatrix}},}$$ ve druhé rovnosti jsou použity součtové vzorce. Výsledné složení odpovídá rotaci o úhel ${\displaystyle \alpha +\beta }$, jak lze očekávat.

Skalární součin, bilineární forma a seskvilineární forma

Standardní skalární součin dvou reálných sloupcových vektorů lze zapsat maticovým součinem

${\displaystyle {\boldsymbol {x}}^{\mathsf {T}}{\boldsymbol {y}},}$

kde ${\displaystyle {\boldsymbol {x}}^{\mathsf {T}}}$ je řádkový vektor získaný pomocí transpozice ${\displaystyle {\boldsymbol {x}}}$. (Výsledná matice ${\displaystyle 1\times 1}$ je zde ztotožněna se svým jediným prvkem.)

Obecněji lze jakoukoli bilineární formu ve vektorovém prostoru konečného rozměru vyjádřit jako maticový součin

${\displaystyle {\boldsymbol {x}}^{\mathsf {T}}{\boldsymbol {Ay}},}$

a jakoukoliv seskvilineární formu lze vyjádřit jako

${\displaystyle {\boldsymbol {x}}^{\mathsf {H}}{\boldsymbol {Ay}},}$

kde ${\displaystyle {\boldsymbol {x}}^{\mathsf {H}}}$ je hermitovsky sdružený vektor k vektoru ${\displaystyle {\boldsymbol {x}}}$.

Alokace zdrojů v ekonomii

Výpočet prvku v levém dolním rohu součinu ${\displaystyle {\boldsymbol {AB}}}$ odpovídá všem možným cestám (zvýrazněné) od suroviny ${\displaystyle b_{4}}$ ke konečnému výrobku ${\displaystyle f_{1}}$ v grafu toku výroby.

Jako příklad si představme fiktivní továrnu, která používá 4 druhy surovin ${\displaystyle b_{1},b_{2},b_{3},b_{4}}$ k výrobě 3 meziproduktů, ${\displaystyle m_{1},m_{2},m_{3}}$, které se následně používají k výrobě 3 druhů výrobků, ${\displaystyle f_{1},f_{2},f_{3}}$.

Matice ${\displaystyle {\boldsymbol {A}}={\begin{pmatrix}1&0&1\\2&1&1\\0&1&1\\1&1&2\\\end{pmatrix}}}$   a   ${\displaystyle {\boldsymbol {B}}={\begin{pmatrix}1&2&1\\2&3&1\\4&2&2\\\end{pmatrix}}}$ udávají množství surovin potřebných pro výrobu meziproduktů, respektive množství meziproduktů potřebných pro výsledné výrobky. Například k výrobě jednoho meziproduktu ${\displaystyle m_{1}}$ je třeba jedna jednotka suroviny ${\displaystyle b_{1}}$, dvě jednotky ${\displaystyle b_{2}}$, žádné ${\displaystyle b_{3}}$ a jedna jednotka ${\displaystyle b_{4}}$, což odpovídá prvnímu sloupci matice ${\displaystyle {\boldsymbol {A}}}$.

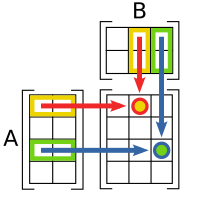
Součin ${\displaystyle {\boldsymbol {AB}}={\begin{pmatrix}5&4&3\\8&9&5\\\ 6&5&3\\11&9&6\\\end{pmatrix}}}$ pak přímo udává množství surovin potřebných pro výrobu jednotlivých výrobků. Například prvek v levém dolním rohu ${\displaystyle {\boldsymbol {AB}}}$ je vypočítán jako ${\displaystyle 1\cdot 1+1\cdot 2+2\cdot 4=11}$, což odpovídá tomu, že ${\displaystyle 11}$ jednotek ${\displaystyle b_{4}}$ je potřeba k výrobě jednoho výrobku ${\displaystyle f_{1}}$. Jmenovitě jedna jednotka ${\displaystyle b_{4}}$ je třeba pro ${\displaystyle m_{1}}$, 2 pro ${\displaystyle m_{2}}$ a ${\displaystyle 4}$ pro každý ze dvou meziproduktů ${\displaystyle m_{3}}$, které jsou potřeba pro jeden kus ${\displaystyle f_{1}}$, viz obrázek.

Aby bylo možné vyrobit např. 100 výrobků ${\displaystyle f_{1}}$, 80 ${\displaystyle f_{2}}$ a 60 ${\displaystyle f_{3}}$, lze potřebné množství surovin vypočítat jako

${\displaystyle ({\boldsymbol {AB}}){\begin{pmatrix}100\\80\\60\\\end{pmatrix}}={\begin{pmatrix}1000\\1820\\1180\\2180\end{pmatrix}},}$

tj. ${\displaystyle 1000}$ jednotek ${\displaystyle b_{1}}$, ${\displaystyle 1820}$ jednotek ${\displaystyle b_{2}}$, ${\displaystyle 1180}$ jednotek ${\displaystyle b_{3}}$ a ${\displaystyle 2180}$ jednotek ${\displaystyle b_{4}}$.Matice součinu ${\displaystyle {\boldsymbol {AB}}}$ může být použita k výpočtu množství surovin i pro jiné počty výrobků.^[3]

Vlastnosti

Rovnosti uvedené v následujících odstavcích platí, pokud mají výsledky operací smysl.

• Součin matice ${\displaystyle {\boldsymbol {A}}}$ s jednotkovou maticí ${\displaystyle \mathbf {I} }$ zprava i zleva má za výsledek matici ${\displaystyle {\boldsymbol {A}}}$, tj. ${\displaystyle \mathbf {I} {\boldsymbol {A}}={\boldsymbol {A}}\mathbf {I} ={\boldsymbol {A}}}$.
• Maticový součin je asociativní, tedy ${\displaystyle {\boldsymbol {A}}({\boldsymbol {B}}{\boldsymbol {C}})=({\boldsymbol {A}}{\boldsymbol {B}}){\boldsymbol {C}}}$.
• Maticový součin není komutativní, tedy existují příklady matic, pro něž platí ${\displaystyle {\boldsymbol {AB}}\neq {\boldsymbol {BA}}}$.
• Maticový součin je distributivní vůči sčítání, tj. ${\displaystyle {\boldsymbol {A}}\left({\boldsymbol {B}}+{\boldsymbol {C}}\right)={\boldsymbol {AB}}+{\boldsymbol {AC}}}$.
• Maticový součin je lineární vůči násobení skalárem (typicky reálné nebo komplexní číslo), tj. ${\displaystyle {\boldsymbol {A}}\left(c{\boldsymbol {B}}\right)=(c{\boldsymbol {A}}){\boldsymbol {B}}=c({\boldsymbol {A}}{\boldsymbol {B}})}$.
• Matice vzhledem k součinu mohou být dělitelé nuly, tj. součin dvou nenulových matic může být nulová matice, například

${\displaystyle {\begin{pmatrix}1&1\\2&2\end{pmatrix}}{\begin{pmatrix}-3\\3\end{pmatrix}}={\begin{pmatrix}0\\0\end{pmatrix}}}$.

• Součin matic ${\displaystyle {\boldsymbol {A}}}$ typu ${\displaystyle m\times n}$ a ${\displaystyle {\boldsymbol {B}}}$ typu ${\displaystyle n\times p}$ lze vyjádřit jako

${\displaystyle {\boldsymbol {AB}}={\boldsymbol {a}}_{1}{\boldsymbol {b}}_{1}^{\mathsf {T}}+{\boldsymbol {a}}_{2}{\boldsymbol {b}}_{2}^{\mathsf {T}}+\cdots +{\boldsymbol {a}}_{n}{\boldsymbol {b}}_{n}^{\mathsf {T}}}$,
kde ${\displaystyle {\boldsymbol {a}}_{1},{\boldsymbol {a}}_{2},\dots ,{\boldsymbol {a}}_{n}}$ jsou sloupce matice ${\displaystyle {\boldsymbol {A}}}$ a ${\displaystyle {\boldsymbol {b}}_{1}^{\mathsf {T}},{\boldsymbol {b}}_{2}^{\mathsf {T}},\dots ,{\boldsymbol {b}}_{n}^{\mathsf {T}}}$ řádky matice ${\displaystyle {\boldsymbol {B}}}$. (Neboli ${\displaystyle {\boldsymbol {b}}_{1},{\boldsymbol {b}}_{2},\dots ,{\boldsymbol {b}}_{n}}$ jsou sloupce ${\displaystyle {\boldsymbol {B}}^{\mathsf {T}}}$.) Zde každý sčítanec ${\displaystyle {\boldsymbol {a}}_{i}{\boldsymbol {b}}_{i}^{\mathsf {T}}}$ je matice typu ${\displaystyle m\times p}$, protože sloupcové vektory odpovídají maticím o jednom sloupci.

• Transpozice součinu matic je součin transponovaných matic v opačném pořadí, tj. ${\displaystyle {({\boldsymbol {AB}})}^{\mathsf {T}}={\boldsymbol {B}}^{\mathsf {T}}{\boldsymbol {A}}^{\mathsf {T}}}$
• Inverzní matice součinu regulárních matic je součin inverzních matic v opačném pořadí, tj. ${\displaystyle {({\boldsymbol {AB}})}^{-1}={\boldsymbol {B}}^{-1}{\boldsymbol {A}}^{-1}}$
• Hermitovské sdružení (hermitovská transpozice) součinu matic je součin matic hermitovsky sdružených v opačném pořadí, tj. ${\displaystyle {({\boldsymbol {AB}})}^{\mathsf {H}}={\boldsymbol {B}}^{\mathsf {H}}{\boldsymbol {A}}^{\mathsf {H}}}$
• Maticový součin odpovídá skládání lineárních zobrazení, které matice reprezentují.

Součiny čtvercových matic

Mocniny matice

Čtvercovou matici lze umocnit na jakoukoli nezápornou celočíselnou mocninu tím, že ji opakovaně násobíme stejným způsobem jako u běžných čísel, konkrétně

${\displaystyle {\boldsymbol {A}}^{0}=\mathbf {I} ,}$

${\displaystyle {\boldsymbol {A}}^{1}={\boldsymbol {A}},}$

${\displaystyle {\boldsymbol {A}}^{k}=\underbrace {{\boldsymbol {A}}{\boldsymbol {A}}\cdots {\boldsymbol {A}}} _{k{\text{ krát}}}.}$

Výpočet ${\displaystyle k}$-té mocniny matice potřebuje ${\displaystyle k-1}$ maticových součinů, pokud se provádí triviálním algoritmem (opakované násobení). Protože to může být velmi časově náročné, obecně se dává přednost použití umocňování pomocí druhé mocniny, které vyžaduje nejvýše ${\displaystyle \log _{2}k}$ maticových součinů, a je tedy mnohem efektivnější.

Snadným případem umocňování je diagonální matice. Protože součin diagonálních matic se rovná prostému vynásobení odpovídajících diagonálních prvků dohromady, získáme ${\displaystyle k}$-tou mocninu diagonální matice umocněním prvků na diagonále na ${\displaystyle k}$-tou:

${\displaystyle {\begin{pmatrix}a_{11}&0&\cdots &0\\0&a_{22}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &a_{nn}\end{pmatrix}}^{k}={\begin{pmatrix}a_{11}^{k}&0&\cdots &0\\0&a_{22}^{k}&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &a_{nn}^{k}\end{pmatrix}}.}$

Regulární a singulární matice

Označme ${\displaystyle {\mathcal {M}}_{n}(R)}$ množinu čtvercových matic řádu ${\displaystyle n}$ s prvky z okruhu ${\displaystyle R}$, což je v praxi často těleso.

V ${\displaystyle {\mathcal {M}}_{n}(R)}$ je součin definován pro každou dvojici matic. Toto dělá z ${\displaystyle {\mathcal {M}}_{n}(R)}$ okruh, který má jednotkovou matici ${\displaystyle \mathbf {I} }$ za neutrální prvek.

Pokud je ${\displaystyle n>1}$, mnoho matic nemá inverzní prvek vůči násobení, např. nulová matice. Pokud inverzní prvek existuje, značí se ${\displaystyle {\boldsymbol {A}}^{-1}}$ a nazývá se inverzní matice k matici ${\displaystyle {\boldsymbol {A}}}$. Splňuje:

${\displaystyle {\boldsymbol {A}}{\boldsymbol {A}}^{-1}={\boldsymbol {A}}^{-1}{\boldsymbol {A}}=\mathbf {I} .}$

Matice, která má inverzi, je regulární matice, někdy též invertibilní matice. Pokud inverzní matici nemá, nazývá se singulární matice.

Součin matic ${\displaystyle {\boldsymbol {AB}}}$ je regulární, právě když je každý z činitelů ${\displaystyle {\boldsymbol {A}}}$ i ${\displaystyle {\boldsymbol {B}}}$ regulární. V tomto případě platí

${\displaystyle ({\boldsymbol {AB}})^{-1}={\boldsymbol {B}}^{-1}{\boldsymbol {A}}^{-1}.}$

Determinant součinu

Determinant součinu čtvercových matic je součin jejich determinantů.

${\displaystyle \det({\boldsymbol {AB}})=\det({\boldsymbol {BA}})=\det {\boldsymbol {A}}\,\det {\boldsymbol {B}}}$.

Tento vztah platí kdykoli je ${\displaystyle R}$ komutativní okruh, jmenovitě i v tělesech.

Výpočetní složitost

Výpočetní složitost výše popsaného algoritmu je ${\displaystyle O(n^{3})}$ (počítáme ${\displaystyle n^{2}}$ čísel; pro každé potřebujeme ${\displaystyle 2n-1}$ aritmetických operací). Existují však algoritmy s nižší složitostí vhodné pro matice vyšších řádů. Nejpoužívanější z nich je Strassenův algoritmus se složitostí ${\displaystyle O(n^{\log _{2}{7}})\approx O(n^{2.807})}$. Nižší složitost u tohoto algoritmu však získáváme za cenu snížené numerické stability. Asymptoticky nejrychlejší ze známých algoritmů je Coppersmithův-Winogradův algoritmus (${\displaystyle O(n^{2.376})}$), který je však použitelný až pro matice tak velkých řádů, že je nelze zpracovávat pomocí současných počítačů^[4].

Teoreticky by se dala složitost ještě snížit, ale nikdy nemůže být menší než ${\displaystyle O(n^{2})}$, protože je třeba spočítat ${\displaystyle n^{2}}$ čísel.

Hledání nejkratší cesty v grafu

Algoritmy pro násobení matic s malou výpočetní složitostí lze využít i pro hledání nejkratší cesty v grafu z každého do každého vrcholu. To má v nejjednodušší podobě složitost ${\displaystyle O(n^{3})}$. V tomto případě se však nepoužívá zde popsané násobení matic, ale upravená verze, kde je místo sčítání výběr nejmenšího prvku a místo násobení sčítání, proto nelze použít například Strassenův algoritmus, který využívá operaci odčítání jako inverzní operaci ke sčítání, která k operaci ${\displaystyle \min }$ není.

Graf lze popsat maticí vzdáleností ${\displaystyle {\boldsymbol {A}}}$. Pokud je pro výpočty operace sčítání dvou čísel definována jako jejich minimum, a místo násobení se použije sčítání, je možno matici nejkratších cest ${\displaystyle {\boldsymbol {B}}}$ získat jako (${\displaystyle {\boldsymbol {A}}^{n}}$) kde ${\displaystyle n}$ je řád matice vzdáleností. Při reálném výpočtu není třeba cyklicky násobit původní maticí, ale vždy se vynásobí vzniklé výsledky - nejkratší cesty jsou získány po ${\displaystyle \log _{2}(n)}$ násobeních. Je-li použit pro násobení algoritmus se složitostí menší než ${\displaystyle O{\biggl (}{\frac {n^{3}}{\log _{2}(n)}}{\biggr )}}$, složitost hledání cest se tímto postupem sníží.

Odkazy

Reference

V tomto článku byl použit překlad textu z článku Matrix multiplication na anglické Wikipedii.

1. Slovník školské matematiky. Praha: SPN, 1981. 240 s.
2. ČSN EN ISO 80000-2 (011300). Veličiny a jednotky - Část 2: Matematika. Česká agentura pro standardizaci, 2020-11-01. detail.
3. Peter Stingl. Mathematik für Fachhochschulen – Technik und Informatik. 5th. vyd. Munich: Carl Hanser Verlag, 1996. ISBN 3-446-18668-9. (German)Je zde použita šablona {{Cite book}} označená jako k „pouze dočasnému použití“. Zde: příklad 5.4.10, s.205-206
4. Robinson, Sara (2005), "Toward an Optimal Algorithm for Matrix Multiplication Archivováno 31. 3. 2010 na Wayback Machine.", SIAM News 38 (9), http://www.siam.org/pdf/news/174.pdf Archivováno 31. 3. 2010 na Wayback Machine.

Literatura

• BÄRTSCH, Hans-Jochen. Matematické vzorce. Praha: Academia, 2006. 832 s. ISBN 80-200-1448-9. Kapitola Matice, s. 180–198.
• BEČVÁŘ, Jindřich. Lineární algebra. 1. vyd. Praha: Matfyzpress, 2019. 436 s. ISBN 978-80-7378-392-1.
• HLADÍK, Milan. Lineární algebra (nejen) pro informatiky. 1. vyd. Praha: Matfyzpress, 2019. 328 s. ISBN 978-80-7378-378-5. S. 39.
• OLŠÁK, Petr. Lineární algebra [online]. Praha: 2007 [cit. 2023-02-20]. Dostupné online.
• MOTL, Luboš; ZAHRADNÍK, Miloš. Pěstujeme lineární algebru [online]. [cit. 2023-02-20]. Dostupné online.

Související články

• Hadamardův součin
• Skalární součin, Vnitřní součin
• Smíšený součin
• Strassenův algoritmus
• Tenzorový součin, Vnější součin
• Vektorový součin, Dvojitý vektorový součin

Externí odkazy

• Obrázky, zvuky či videa k tématu násobení matic na Wikimedia Commons
• Lineární algebra: algebra matic Archivováno 16. 2. 2009 na Wayback Machine. Aplikace, která násobí a sčítá matice zadané uživatelem a zobrazuje postup výpočtu.

Portály: Matematika