Procés estocàstic

En teoria de probabilitat i generalment en el camp estadístic, un procés aleatori o procés estocàstic és un concepte matemàtic normalment definit com un conjunt de variables aleatòries.^[1][2] El seu estudi és el camp matemàtic de l’estocàstica.

L'índex borsari és un exemple de procés estocàstic de tipus no estacionari (per això no es pot predir)

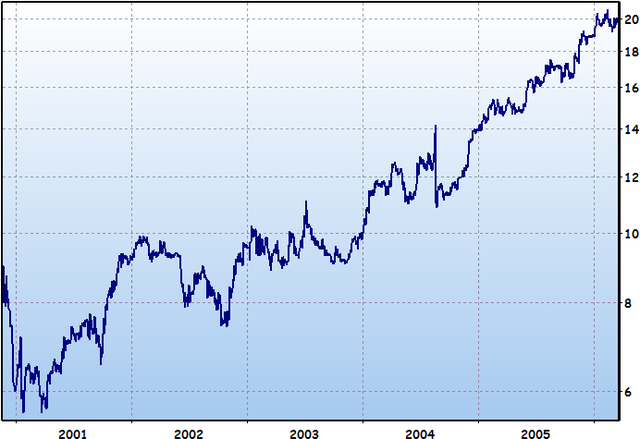
Els processos estocàstics s’acostumen a utilitzar com a models matemàtics de sistemes i fenòmens que acostumen a variar de forma aleatòria. Alguns exemples inclourien el creixement d’una població bacteriana, el corrent elèctric que fluctua a causa del soroll tèrmic, o bé el moviment d’una molècula de gas.

Els processos estocàstics tenen moltes aplicacions en diversos camps, com ara la biologia, l'ecologia, la informàtica, la neurociència, la química i moltes altres. En especial es podria mencionar el seu impacte en el sector financer després de veure grans canvis aleatoris en els mercats d’aquest sector.

Etimologia

El terme prové de l'adjectiu de l’antic grec στοχαστικος (stochastikos), que va derivar en el significat de «conjectural»,^[3] i que en origen volia dir «hàbil apuntant», especialment referit als arquers. Al seu torn, l’adjectiu prové de stochazesthai , apuntar, suposar, de stochos diana.

Introducció

Un procés aleatori o estocàstic pot ser definit com una col·lecció de variables que estan dins d’un conjunt matemàtic. Això voldria dir que cada variable aleatòria del procés estocàstic estaria únicament associada amb un element del conjunt matemàtic. Històricament el conjunt d’índex on es col·loquen les variables aleatòries era definit com un subconjunt de l'eix real, com ara l'eix dels nombres naturals, donant al conjunt d’índex la interpretació del temps. Cada variable del conjunt pren valors del mateix espai matemàtic, conegut com estat espai. Alguns exemples d’aquest estat poden ser els nombres enters, l'eix real o bé l'espai Euclidià n-dimensional.

Un procés estocàstic pot tenir varis resultats degut a la seva aleatorietat. En cas de tenir un resultat simple el procés s’anomena realització o funció mostra.

Classificacions

Els processos estocàstics poden classificar-se de diverses maneres. Segons el seu estat espai, el conjunt d’índex o segons la dependència entre les variables aleatòries. Una forma molt comú de classificar és per la cardinalitat del conjunt d’índex i de l'estat espai.

Quan ho interpretem com a temps, si l’índex d’un conjunt estocàstic té un nombre finit o comptable d’elements com ara un conjunt de nombres, el conjunt d’enters o de nombres naturals, aleshores el procés estocàstic es diu que és discret. Si l’índex en canvi és en un interval de l'eix real aleshores és continu. Els processos estocàstics discrets són considerats més fàcils d’estudiar ja que els processos continus requereixen tècniques matemàtiques més avançades i coneixement, particularment degut a que el seu índex és incomptable. Si l’índex són els enters o qualsevol subconjunt d’aquests aleshores el procés estocàstic pot anomenar-se seqüència aleatòria.

Terminologia

La definició de procés estocàstic varia, tot i així un procés estocàstic ha estat tradicionalment definit com una col·lecció de variables aleatòries indexades per un conjunt. El terme procés aleatori és un sinònim de procés estocàstic i són utilitzats pel mateix.

El terme de funció aleatòria s’acostuma a utilitzar com a procés aleatori, tot i que a vegades només s’utilitza quan el procés estocàstic pren valors reals. També s’utilitza quan el conjunt d’índex es un espai matemàtic diferent de l'eix real, mentre que el terme procés estocàstic s’utilitza quan el conjunt d’índex s’interpreta com a temporal.

Notació

Un procés estocàstic pot ser definit com ${\displaystyle {\displaystyle X(t)_{t\in T}}}$, ${\displaystyle {\displaystyle \{X_{t}\}_{t\in T}}}$, ${\displaystyle {\displaystyle X_{t}}}$, ${\displaystyle {\displaystyle X(t)}}$ o simplement ${\displaystyle {\displaystyle X}}$ o ${\displaystyle {\displaystyle X(t)}}$. Tot i que l’ús de ${\displaystyle {\displaystyle X(t)}}$ és considerat com un abús de la notació. Per exemple, ${\displaystyle {\displaystyle X(t)}}$ or ${\displaystyle {\displaystyle X_{t}}}$ s’utilitzen per referir-se a variables aleatoris amb índex ${\displaystyle {\displaystyle t}}$, i no a processos estocàstics. Si el conjunt d’índex és ${\displaystyle {\displaystyle T=[0,\infty )}}$, aleshores és pot escriure ${\displaystyle {\displaystyle (X_{t},t\geq 0)}}$ per denotar el procés estocàstic.

Exemples

Procés Bernoulli

Un dels processos estocàstics més simples és el procés de Bernoulli, que és una seqüència de variables aleatòries independents i idènticament distribuïdes (iid), on cada variable aleatòria pren el valor un o zero, per exemple, un amb probabilitat ${\displaystyle {\displaystyle p}}$ i zero amb probabilitat ${\displaystyle {\displaystyle 1-p}}$. Aquest procés es pot relacionar amb tirar repetidament una moneda, on hi ha la probabilitat d'obtenir un cap ${\displaystyle {\displaystyle p}}$ i el seu valor és un, mentre que el valor d'una creu és zero. En altres paraules, un procés de Bernoulli és una seqüència de variables aleatòries iid de Bernoulli, on cada llançament de moneda és un exemple d'un assaig de Bernoulli.

Caminada aleatòria

Els camins aleatoris són processos estocàstics que solen definir-se com a sumes de variables aleatòries iid o vectors aleatoris en l'espai euclidià, de manera que són processos que canvien en un temps discret. Però alguns també utilitzen el terme per referir-se a processos que canvien en un temps continu, particularment el procés de Wiener utilitzat en finances, que ha provocat certa confusió, resultant en la seva crítica. Hi ha altres tipus diversos de caminades aleatòries, definits de manera que els seus espais d'estats poden ser altres objectes matemàtics, com ara reticles i grups, i en general estan molt estudiats i tenen moltes aplicacions en diferents disciplines.

Un exemple clàssic de caminada aleatòria es coneix com a caminada aleatòria simple, que és un procés estocàstic en temps discret amb els nombres enters com a espai d'estats, i es basa en un procés de Bernoulli, on cada variable de Bernoulli pren el valor positiu o bé negatiu. En altres paraules, la caminada aleatòria simple té lloc sobre els nombres enters, i el seu valor augmenta en un amb probabilitat, per exemple, ${\displaystyle {\displaystyle p}}$, o disminueix en un amb probabilitat ${\displaystyle {\displaystyle 1-p}}$, de manera que el conjunt d'índexs d'aquesta caminada aleatòria són els nombres naturals, mentre que el seu espai d'estats són els nombres enters. Si el ${\displaystyle {\displaystyle p=0,5}}$, aquesta caminada aleatòria s'anomena caminada aleatòria simètrica.

Procés Wiener

El procés de Wiener és un procés estocàstic amb increments estacionaris i independents que es distribueixen normalment en funció de la mida dels increments. El procés de Wiener rep el nom de Norbert Wiener, que va demostrar la seva existència matemàtica, però el procés també s'anomena procés de moviment brownià o simplement moviment brownià a causa de la seva connexió històrica com a model del moviment brownià en líquids.

Jugant un paper central en la teoria de la probabilitat, el procés de Wiener sovint es considera el procés estocàstic més important i estudiat, amb connexions amb altres processos estocàstics. El seu conjunt d'índexs i l'espai d'estats són els nombres no negatius i els nombres reals, respectivament, de manera que té tant un conjunt d'índexs continus com un espai d'estats. Però el procés es pot definir de manera més general, de manera que el seu espai d'estats pot ser ${\displaystyle {\displaystyle n}}$-espai euclidià dimensional. Si la mitjana de qualsevol increment és zero, es diu que el procés de moviment de Wiener o Brownià resultant té un desplaçament estocàstic zero. Si la mitjana de l'increment per a dos punts de temps qualsevol és igual a la diferència de temps multiplicada per alguna constant ${\displaystyle {\displaystyle \mu }}$, que és un nombre real, llavors es diu que el procés estocàstic resultant té un desplaçament estocàstic ${\displaystyle {\displaystyle \mu }}$.

Quasi sempre, un camí de mostra d'un procés de Wiener és continu a tot arreu però enlloc diferenciable. Es pot considerar com una versió contínua de la caminada aleatòria simple. El procés sorgeix com el límit matemàtic d'altres processos estocàstics com ara certs camins aleatoris reescalats, que és l'objecte del teorema de Donsker o principi d'invariància, també conegut com el teorema del límit central funcional.

El procés de Wiener és membre d'algunes famílies importants de processos estocàstics, inclosos els processos de Markov, els processos de Lévy i els processos gaussians. El procés també té moltes aplicacions i és el principal procés estocàstic utilitzat en el càlcul estocàstic. Té un paper central en les finances quantitatives, on es fa servir, per exemple, en el model Black–Scholes–Merton. El procés també s'utilitza en diferents camps, incloent-hi la majoria de les ciències naturals així com algunes branques de les ciències socials, com a model matemàtic per a diversos fenòmens aleatoris.

Definició matemàtica

Un procés estocàstic es pot definir equivalentment de dues maneres diferents:

• Com un conjunt de realitzacions temporals i un índex aleatori que selecciona una d'elles.
• Com un conjunt de variables aleatòries ${\displaystyle X_{T}\,}$ indexades per un índex ${\displaystyle t\,}$, atès que ${\displaystyle t\in T\,}$, amb ${\displaystyle T\subseteq \mathbb {(} R)\,}$.

${\displaystyle T\,}$ pot ser continu si és un interval (el nombre dels seus valors és il·limitat) o discret si és numerable (només pot assumir determinats valors).

Les variables aleatòries ${\displaystyle X_{T}\,}$ prenen valors en un conjunt que s'anomena espai probabilístic.

Sigui ${\displaystyle (\Omega ,{\mathcal {B}},P)}$ un espai probabilístic.

En una mostra de mida ${\displaystyle n}$ s'observa un succés compost ${\displaystyle E}$ format per successos elementals ${\displaystyle \omega }$:

${\displaystyle E=\{\omega _{1},\omega _{2},...,\omega _{n}\}\subset \Omega \,}$, de manera que ${\displaystyle E\in B\,}$.

El succés compost és un subconjunt contingut en l'espai mostral i és una àlgebra de Boole ${\displaystyle B}$. A cada succés ${\displaystyle \omega }$ li correspon un valor d'una variable aleatòria ${\displaystyle V}$, de manera que ${\displaystyle V}$ és funció de ${\displaystyle \omega }$:

${\displaystyle V=V(\omega );\qquad \omega \in \Omega ,\,-\infty <V<\infty }$

El domini d'aquesta funció és a dir el camp de variabilitat del succés elemental, és l'espai mostral, i la seva recorregut, o sigui el de la variable aleatòria, és el camp dels nombres reals. Es diu procés aleatori al valor en ${\displaystyle (A,{\mathcal {A}})}$ d'un element ${\displaystyle X=(\Omega ,{\mathcal {B}},(X_{T})_{(}t\geq 0),P)}$, on per a tot ${\displaystyle t\in \mathbb {(} R),X_{T}\,}$ és una variable aleatòria del valor en ${\displaystyle (A,{\mathcal {A}})}$.

Si s'observa el succés ${\displaystyle \omega }$ en un moment ${\displaystyle t}$ de temps:

${\displaystyle V=V(\omega ,t),\qquad \omega \in \Omega ,t\in T,-\infty <V<\infty }$.

${\displaystyle V}$ defineix així un procés estocàstic.^[4]

Si ${\displaystyle (({\mathcal {B}})_{T})_{T}\,}$ és una filtració,^[5] s'anomena procés aleatori adaptat, al valor en ${\displaystyle (A,{\mathcal {A}})}$, d'un element ${\displaystyle X=(\omega ,{\mathcal {B}},{\mathcal {(}}B)_{T},(X_{T})_{T},P)}$, on ${\displaystyle X_{T}\,}$ és una variable aleatòria ${\displaystyle {\mathcal {(}}B)_{T}}$-mesurable del valor en ${\displaystyle (A,{\mathcal {A}})}$. La funció ${\displaystyle \mathbb {R} \rightarrow A\$ :\ t\mapsto X_{t}(\omega )} es diu la trajectòria associada al succés ${\displaystyle \omega \,}$.

Casos especials

• Procés estacionari: Un procés és estacionari en sentit estricte si la funció de distribució conjunta de qualsevol subconjunt de variables és constant respecte a un desplaçament en el temps. Es diu que un procés és estacionari en sentit ampli (o dèbilment estacionari) quan es verifica que:

1. La mitjana teòrica és independent del temps, i
2. Les autocovariances d'ordres només venen afectades pel lapse de temps transcorregut entre els dos períodes i no depenen del temps.

• Procés homogeni: És el que té variables aleatòries independents i idènticament distribuïdes
• Procés de Markov: Un procés discret en què l'evolució només depèn de l'estat actual i no dels anteriors.
• Procés de Gauss: Un procés continu en el que tota combinació lineal de variables és una variable de distribució normal.
• Procés de Poisson: És un procés continu en el temps
• Procés de Gauss-Markov: És un procés, al mateix temps, de Gauss i de Markov
• Procés de Bernoulli És un procés discret amb una distribució binomial.

Definicions

Procés estocàstic

Un procés estocàstic es defineix com una col·lecció de variables aleatòries definides en un espai de probabilitat comú ${\displaystyle {\displaystyle (\Omega ,{\mathcal {F}},P)}}$, on ${\displaystyle {\displaystyle \Omega }}$ és un espai mostral ,${\displaystyle {\displaystyle {\mathcal {F}}}}$ és un ${\displaystyle {\displaystyle \sigma }}$- àlgebra, i ${\displaystyle {\displaystyle P}}$ és una mesura de probabilitat. Les variables aleatòries, indexades per algun conjunt ${\displaystyle {\displaystyle T}}$, prenen valors en el mateix espai matemàtic ${\displaystyle {\displaystyle S}}$, que ha de ser mesurable respecte a alguna ${\displaystyle {\displaystyle \sigma }}$-àlgebra.

.En altres paraules, per a un espai de probabilitat donat ${\displaystyle {\displaystyle (\Omega ,{\mathcal {F}},P)}}$ i un espai mesurable ${\displaystyle {\displaystyle (S,\Sigma )}}$, un procés estocàstic és una col·lecció de ${\displaystyle {\displaystyle S}}$-variables aleatòries que es poden escriure com: ${\displaystyle {\displaystyle \{X(t):t\in T\}.}}$

Històricament, en molts problemes des de les ciències naturals un punt ${\displaystyle {\displaystyle t\in T}}$ feia referència al temps, ja que ${\displaystyle {\displaystyle X(t)}}$ és una variable aleatòria que representa un valor observat en el temps ${\displaystyle {\displaystyle t}}$. Un procés estocàstic també es pot escriure com ${\displaystyle {\displaystyle \{X(t,\omega ):t\in T\}}}$ per reflectir que en realitat és una funció de dues variables: ${\displaystyle {\displaystyle t\in T}}$ i ${\displaystyle {\displaystyle \omega \in \Omega }}$.

Hi ha altres maneres de definir un procés estocàstic, considerant la definició anterior la tradicional. Per exemple, un procés estocàstic es pot interpretar com la ${\displaystyle {\displaystyle S^{T}}}$-variable aleatòria, on ${\displaystyle {\displaystyle S^{T}}}$ és l'espai de totes les possibles ${\displaystyle {\displaystyle S}}$ funcions de ${\displaystyle {\displaystyle t\in T}}$.

Conjunt d'índexs

El conjunt ${\displaystyle {\displaystyle T}}$ s'anomena conjunt d'índexs o conjunt de paràmetres del procés estocàstic. Sovint, aquest conjunt és algun subconjunt de la recta real, com ara els nombres naturals o un interval, que dona al conjunt ${\displaystyle {\displaystyle T}}$ la interpretació del temps. A més d'aquests conjunts, el conjunt d'índexs ${\displaystyle {\displaystyle T}}$ pot ser un altre conjunt amb un ordre total o un conjunt més general, com el pla cartesià ${\displaystyle {\displaystyle R^{2}}}$ o l’${\displaystyle {\displaystyle n}}$-espai euclidià, on un element ${\displaystyle {\displaystyle t\in T}}$ pot representar un punt de l'espai. Dit això, molts resultats i teoremes només són possibles per a processos estocàstics amb un conjunt d'índexs totalment ordenat.

Espai d’estat

L' espai matemàtic ${\displaystyle {\displaystyle S}}$ d'un procés estocàstic s'anomena espai d'estats. Aquest espai matemàtic es pot definir mitjançant nombres enters, rectes reals, ${\displaystyle {\displaystyle n}}$-espais euclidians, plans complexos o espais matemàtics més abstractes. L'espai d'estats es defineix mitjançant elements que reflecteixen els diferents valors que pot prendre el procés estocàstic.

Funció de mostra

Una funció de mostra és un resultat únic d'un procés estocàstic, de manera que es forma prenent un únic valor possible de cada variable aleatòria del procés estocàstic. Més precisament, si ${\displaystyle {\displaystyle \{X(t,\omega ):t\in T\}}}$ és un procés estocàstic, per a qualsevol punt ${\displaystyle {\displaystyle \omega \in \Omega }}$, el mapeig ${\displaystyle {\displaystyle X(\cdot ,\omega ):T\rightarrow S,}}$ s'anomena funció mostra, realització o, especialment quan ${\displaystyle {\displaystyle T}}$ s'interpreta com el temps, un camí mostra del procés estocàstic ${\displaystyle {\displaystyle \{X(t,\omega ):t\in T\}}}$. Això vol dir que, per a un ${\displaystyle {\displaystyle \omega \in \Omega }}$ fixat, existeix una funció de mostra que aplica el conjunt d'índexs ${\displaystyle {\displaystyle T}}$ a l'espai estat ${\displaystyle {\displaystyle S}}$. Altres noms per a una funció mostra d'un procés estocàstic són trajectòria, funció de camí [140] o camí .

Increment

Un increment d'un procés estocàstic és la diferència entre dues variables aleatòries del mateix procés estocàstic. Per a un procés estocàstic amb un conjunt d'índexs que es pot interpretar com a temps, un increment és quant canvia el procés estocàstic en un període determinat. Per exemple, si ${\displaystyle {\displaystyle \{X(t):t\in T\}}}$ és un procés estocàstic amb espai d'estats ${\displaystyle {\displaystyle S}}$ i conjunt d'índexs ${\displaystyle {\displaystyle T=[0,\infty )}}$, llavors per a dos nombres no negatius qualssevol ${\displaystyle {\displaystyle t_{1}\in [0,\infty )}}$ i ${\displaystyle {\displaystyle t_{2}\in [0,\infty )}}$ de tal manera que ${\displaystyle {\displaystyle t_{1}\leq t_{2}}}$, la diferència ${\displaystyle {\displaystyle X_{t_{2}}-X_{t_{1}}}}$ és una ${\displaystyle {\displaystyle S}}$-variable aleatòria coneguda com a increment.

Més definicions

Dret

Per a un procés estocàstic ${\displaystyle {\displaystyle X\colon \Omega \rightarrow S^{T}}}$ definit en l'espai de probabilitat ${\displaystyle {\displaystyle (\Omega ,{\mathcal {F}},P)}}$, la llei del procés estocàstic${\displaystyle {\displaystyle X}}$ es defineix com la mesura de la imatge :${\displaystyle {\displaystyle \mu =P\circ X^{-1},}}$ on ${\displaystyle {\displaystyle P}}$ és una mesura de probabilitat, el símbol ${\displaystyle {\displaystyle \circ }}$ denota composició de funcions i ${\displaystyle {\displaystyle X^{-1}}}$ és la preimatge de la funció mesurable o, de manera equivalent, la ${\displaystyle {\displaystyle S^{T}}}$-variable aleatòria${\displaystyle {\displaystyle X}}$, on ${\displaystyle {\displaystyle S^{T}}}$ és l'espai de totes les possibles ${\displaystyle {\displaystyle S}}$-funcions valorades de ${\displaystyle {\displaystyle t\in T}}$. Per tant, la llei d'un procés estocàstic és una mesura de probabilitat. Per a un subconjunt mesurable ${\displaystyle {\displaystyle B}}$ de ${\displaystyle {\displaystyle S^{T}}}$, la preimatge de ${\displaystyle {\displaystyle X}}$ dona ${\displaystyle {\displaystyle X^{-1}(B)=\{\omega \in \Omega :X(\omega )\in B\},}}$ llavors la llei d'${\displaystyle {\displaystyle X}}$ es pot escriure com: ${\displaystyle {\displaystyle \mu (B)=P(\{\omega \in \Omega :X(\omega )\in B\}).}}$

El dret d'un procés estocàstic o una variable aleatòria és també anomenada la llei de probabilitat, distribució de probabilitat, o la distribució.

Distribucions de probabilitat de dimensions finites

Per a un procés estocàstic ${\displaystyle {\displaystyle X}}$ amb la llei ${\displaystyle {\displaystyle \mu }}$, la seva distribució de dimensions finites per${\displaystyle {\displaystyle t_{1},\dots ,t_{n}\in T}}$ es defineix com: ${\displaystyle {\displaystyle \mu _{t_{1},\dots ,t_{n}}=P\circ (X({t_{1}}),\dots ,X({t_{n}}))^{-1},}}$.

Aquesta mesura ${\displaystyle {\displaystyle \mu _{t_{1},...,t_{n}}}}$ es pot veure com una "projecció" de la llei ${\displaystyle {\displaystyle \mu }}$ a un subconjunt finit de ${\displaystyle {\displaystyle T}}$. Per a qualsevol subconjunt mesurable ${\displaystyle {\displaystyle C}}$, les distribucions de dimensions finites d'un procés estocàstic ${\displaystyle {\displaystyle X}}$ es pot escriure com: ${\displaystyle {\displaystyle \mu _{t_{1},\dots ,t_{n}}(C)=P{\Big (}{\big \{}\omega \in \Omega$ :{\big (}X_{t_{1}}(\omega ),\dots ,X_{t_{n}}(\omega ){\big )}\in C{\big \}}{\Big )}.}}

Les distribucions de dimensions finites d'un procés estocàstic satisfan dues condicions matemàtiques conegudes com a condicions de consistència.

Estacionarietat

L'estacionarietat és una propietat matemàtica que té un procés estocàstic quan totes les variables aleatòries d'aquest es distribueixen de manera idèntica. En altres paraules, si ${\displaystyle {\displaystyle X}}$ és un procés estocàstic estacionari, per a qualsevol ${\displaystyle {\displaystyle t\in T}}$ la variable aleatòria ${\displaystyle {\displaystyle X_{t}}}$ té la mateixa distribució, la qual cosa significa que per a qualsevol conjunt de ${\displaystyle {\displaystyle n}}$ valors ${\displaystyle {\displaystyle t_{1},\dots ,t_{n}}}$, el corresponen ${\displaystyle {\displaystyle n}}$ variables aleatòries ${\displaystyle {\displaystyle X_{t_{1}},\dots X_{t_{n}},}}$, i totes tenen la mateixa distribució de probabilitat. El conjunt d'índexs d'un procés estocàstic estacionari s'acostuma a interpretar com a temps, de manera que poden ser els nombres enters o la recta real. Però el concepte d'estacionarietat també existeix per a processos puntuals i camps aleatoris, on el conjunt d'índexs no s'interpreta com a temps.

Quan s'estableix l'índex ${\displaystyle {\displaystyle T}}$, que es pot interpretar com el temps, es diu que un procés estocàstic és estacionari si les seves distribucions de dimensions finites són invariants respecte les translacions del temps. Aquest tipus de procés estocàstic es pot utilitzar per descriure un sistema físic que es troba en estat estacionari, però encara experimenta fluctuacions aleatòries. La intuïció darrere de l'estacionarietat és que a mesura que passa el temps la distribució del procés estocàstic estacionari segueix sent la mateixa. Una seqüència de variables aleatòries forma un procés estocàstic estacionari només si les variables aleatòries estan distribuïdes de manera idèntica.

De vegades es diu que un procés estocàstic amb la definició anterior d'estacionarietat és estrictament estacionari, però hi ha altres formes d'estacionarietat. Un exemple és quan un procés estocàstic de temps discret o continu ${\displaystyle {\displaystyle X}}$ es diu que és estacionari en el sentit ampli, després el procés ${\displaystyle {\displaystyle X}}$ té un segon moment finit per a tots ${\displaystyle {\displaystyle t\in T}}$ i la covariància de les dues variables aleatòries ${\displaystyle {\displaystyle X_{t}}}$ i ${\displaystyle {\displaystyle X_{t+h}}}$ depèn només del nombre ${\displaystyle {\displaystyle h}}$ per a tot ${\displaystyle {\displaystyle t\in T}}$. Khinchin va introduir el concepte relacionat d'estacionarietat en el sentit ampli, que té altres noms com estacionarietat de covariància o estacionarietat en sentit ampli.

Filtració

Una filtració és una seqüència creixent de ${\displaystyle {\displaystyle \sigma }}$- àlgebres definida en relació a un espai de probabilitat i un conjunt d'índexs que té alguna relació d' ordre total, com en el cas que el conjunt d'índexs sigui algun subconjunt dels nombres reals. Més formalment, si un procés estocàstic té un índex establert amb un ordre total, llavors una filtració ${\displaystyle {\displaystyle \{{\mathcal {F}}_{t}\}_{t\in T}}}$, en un espai de probabilitat ${\displaystyle {\displaystyle (\Omega ,{\mathcal {F}},P)}}$ és una família de ${\displaystyle {\displaystyle \sigma }}$- àlgebres tal que ${\displaystyle {\displaystyle {\mathcal {F}}_{s}\subseteq {\mathcal {F}}_{t}\subseteq {\mathcal {F}}}}$ per a tot ${\displaystyle {\displaystyle s\leq t}}$, on ${\displaystyle {\displaystyle t,s\in T}}$ i ${\displaystyle {\displaystyle \leq }}$ indica l'ordre total del conjunt d'índexs ${\displaystyle {\displaystyle T}}$. Amb el concepte de filtració, és possible estudiar la quantitat d'informació continguda en un procés estocàstic ${\displaystyle {\displaystyle X_{t}}}$ a les ${\displaystyle {\displaystyle t\in T}}$, que es pot interpretar com el temps ${\displaystyle {\displaystyle t}}$.

Modificació

Una modificació d'un procés estocàstic és un altre procés estocàstic, que està estretament relacionat amb el procés estocàstic original. Més precisament, donat un procés estocàstic ${\displaystyle {\displaystyle X}}$ que té el mateix conjunt d'índexs ${\displaystyle {\displaystyle T}}$, establir l'espai ${\displaystyle {\displaystyle S}}$, i l'espai de probabilitat ${\displaystyle {\displaystyle (\Omega ,{\cal {F}},P)}}$ com un altre procés estocàstic ${\displaystyle {\displaystyle Y}}$ es diu que és una modificació de ${\displaystyle {\displaystyle Y}}$ si per a totes les ${\displaystyle {\displaystyle t\in T}}$, es compleix que ${\displaystyle {\displaystyle P(X_{t}=Y_{t})=1,}}$.

Dos processos estocàstics que són modificacions l'un de l'altre tenen la mateixa llei de dimensions finites i es diu que són estocàsticament equivalents o equivalents.

En lloc de modificació, també s'utilitza el terme versió, tanmateix alguns autors utilitzen el terme versió quan dos processos estocàstics tenen les mateixes distribucions de dimensions finites, però es poden definir amb una probabilitat diferent. Si un procés estocàstic de valor real en temps continu compleix determinades condicions de moment en els seus increments, aleshores el teorema de continuïtat de Kolmogorov diu que existeix una modificació d'aquest procés que té camins de mostra continus amb una probabilitat 1, de manera que el procés estocàstic té una modificació contínua o versió. El teorema també es pot generalitzar a camps aleatoris, de manera que el conjunt d'índexs és ${\displaystyle {\displaystyle n}}$-espai euclidià.

Separabilitat

La separabilitat és una propietat d'un procés estocàstic basada en el seu conjunt d'índexs en relació amb la mesura de probabilitat. La propietat s'assumeix de manera que les funcionals de processos estocàstics o camps aleatoris amb conjunts d'índexs incomptables poden formar variables aleatòries. Perquè un procés estocàstic sigui separable, a més d'altres condicions, el seu conjunt d'índexs ha de ser un espai separable, la qual cosa significa que el conjunt d'índexs contingui un subconjunt comptable dens.

Més precisament, un procés estocàstic en temps continu de valor real ${\displaystyle {\displaystyle X}}$amb un espai de probabilitat ${\displaystyle {\displaystyle (\Omega ,{\cal {F}},P)}}$ és separable si el seu índex és conjunt ${\displaystyle {\displaystyle T}}$ conté un subconjunt comptable dens ${\displaystyle {\displaystyle U\subset T}}$ i hi ha un conjunt ${\displaystyle {\displaystyle \Omega _{0}\subset \Omega }}$ de probabilitat zero, per tant ${\displaystyle {\displaystyle P(\Omega _{0})=0}}$, de manera que per a cada conjunt obert ${\displaystyle {\displaystyle G\subset T}}$ i cada conjunt tancat ${\displaystyle {\displaystyle F\subset \textstyle R=(-\infty ,\infty )}}$, els dos esdeveniments ${\displaystyle {\displaystyle \{X_{t}\in F{\text{ per a tot}}t\in G\cap U\}}}$ i ${\displaystyle {\displaystyle \{X_{t}\in F{\text{ per a tot}}t\in G\}}}$ difereixen entre sí com a màxim en un subconjunt de ${\displaystyle {\displaystyle \Omega _{0}}}$. La definició de separabilitat també es pot indicar per a altres conjunts d'índexs i espais d'estats, com en el cas de camps aleatoris, on el conjunt d'índexs i l'espai d'estats pot ser un ${\displaystyle {\displaystyle n}}$-espai euclidià.

El concepte de separabilitat d'un procés estocàstic va ser introduït per Joseph Doob. La idea subjacent de la separabilitat és fer que un conjunt comptable de dots del conjunt d'índexs determini les propietats del procés estocàstic. Qualsevol procés estocàstic amb un conjunt d'índexs comptables ja compleix les condicions de separabilitat, de manera que els processos estocàstics en temps discret són sempre separables. [175] El Teorema de Doob, de vegades conegut com el Teorema de Separabilitat de Doob, diu que qualsevol procés estocàstic en temps continu de valor real té una modificació separable. També existeixen versions d'aquest teorema per a processos estocàstics més generals amb conjunts d'índexs i espais d'estat diferents de la recta real.

Independència

Dos processos estocàstics ${\displaystyle {\displaystyle X}}$ i ${\displaystyle {\displaystyle Y}}$ definits en el mateix espai de probabilitat ${\displaystyle {\displaystyle (\Omega ,{\mathcal {F}},P)}}$ amb el mateix conjunt d'índexs ${\displaystyle {\displaystyle T}}$ es diu que són independents si els vectors aleatoris corresponents són independents.

Incorrelació

Dos processos estocàstics ${\displaystyle {\displaystyle \left\{X_{t}\right\}}}$ i ${\displaystyle {\displaystyle \left\{Y_{t}\right\}}}$ s'anomenen no correlacionats si la seva covariància creuada ${\displaystyle {\displaystyle \operatorname {K} _{\mathbf {X} \mathbf {Y} }(t_{1},t_{2})=\operatorname {E} \left[\left(X(t_{1}))-\mu _{X}(t_{1})\right)\left(Y(t_{2})-\mu _{Y}(t_{2})\right)\right]}}$ és zero en tots els temps. Formalment: ${\displaystyle {\displaystyle \left\{X_{t}\right\},\left\{Y_{t}\right\}{\text{incorrelacionats}}\quad \iff \quad \operatorname {K} _{\mathbf {X} \mathbf {Y} }(t_{1},t_{2})=0\quad \forall t_{1},t_{2}}}$.

Si dos processos estocàstics ${\displaystyle {\displaystyle X}}$ i ${\displaystyle {\displaystyle Y}}$ són independents, llavors tampoc estan correlacionats.

Ortogonalitat

Dos processos estocàstics ${\displaystyle {\displaystyle \left\{X_{t}\right\}}}$ i ${\displaystyle {\displaystyle \left\{Y_{t}\right\}}}$ s'anomenen ortogonals si la seva correlació creuada ${\displaystyle {\displaystyle \operatorname {R} _{\mathbf {X} \mathbf {Y} }(t_{1},t_{2})=\operatorname {E} [X(t_{1}){\overline {Y(t_{2})}}]}}$ és zero en tots els temps.Formalment: ${\displaystyle {\displaystyle \left\{X_{t}\right\},\left\{Y_{t}\right\}{\text{ortogonal}}\quad \iff \quad \operatorname {R} _{\mathbf {X} \mathbf {Y} }(t_{1},t_{2})=0\quad \forall t_{1},t_{2}}}$.

Espai Skorokhod

Un espai de Skorohod és un espai matemàtic de totes les funcions que són contínues per la dreta amb límits per l'esquerra, definits en algun interval de la rect a real com ara ${\displaystyle {\displaystyle [0,1]}}$ o ${\displaystyle {\displaystyle [0,\infty )}}$, i pren valors a la recta real o en algun espai mètric. Aquestes funcions es coneixen com a funcions càdlàg o cadlag, basades en l'acrònim de la frase francesa continue à droite, limite à gauche. Un espai de funció Skorokhod, introduït per Anatoli Skorokhod, sovint es denota amb la lletra ${\displaystyle {\displaystyle D}}$, de manera que l'espai de funció també es coneix com a espai ${\displaystyle {\displaystyle D}}$. La notació d'aquest espai funcional també pot incloure l'interval en què es defineixen totes les funcions càdlàg, així, per exemple, ${\displaystyle {\displaystyle D[0,1]}}$ denota l'espai de les funcions càdlàg definides en l'interval unitari ${\displaystyle {\displaystyle [0,1]}}$.

Els espais de funció de Skorokhod s'utilitzen freqüentment en la teoria dels processos estocàstics perquè sovint s'assumeix que les funcions de mostra dels processos estocàstics de temps continu pertanyen a un espai de Skorokhod. Aquests espais contenen funcions contínues, que corresponen a funcions de mostra del procés de Wiener. Però l'espai també té funcions amb discontinuïtats, la qual cosa significa que les funcions mostrals dels processos estocàstics amb salts, com el procés de Poisson (a la recta real), també són membres d'aquest espai.

Regularitat

En el context de la construcció matemàtica de processos estocàstics, el terme regularitat s'utilitza quan es discuteixen i s'assumeixen determinades condicions perquè un procés estocàstic resolgui possibles problemes de construcció. Per exemple, per estudiar processos estocàstics amb conjunts d'índexs incomptables, s'assumeix que el procés estocàstic s'adhereix a algun tipus de condició de regularitat com ara que les funcions mostrals són contínues.

Història

Teoria de la probabilitat primerenca

La teoria de la probabilitat té el seu origen en els jocs d’atzar, que tenen una llarga historia, però es va fer molt poc anàlisi sobre ells en termes de probabilitat. L’any 1654 a menut es considera el naixement de la teoria de la probabilitat, ja que els matemàtics francesos Pierre Fermat i Blaise Pascal tenien una correspondència escrita sobre la probabilitat, motivada per un problema de joc. Però, abans d’això, va haver un treball matemàtic sobre la probabilitat del joc d’atzar com Liber de Ludo Aleae de Gerolamo Cordano, escrit en el segle XVI però publicat més tard l’any 1663.

Després de Cardano, Jakob Bernoulli va escriure Ars Conjectandi, que es considera un esdeveniment significatiu en la historia de la teoria de la probabilitat. El llibre de Bernoulli va ser publicat en 1713 i, aquest va inspirar a molts matemàtics a estudiar probabilitat. Però, tot hi que alguns matemàtics com Pierre-Simon Laplace, Abraham de Moivre, Carl Gauss, Siméon Poisson i Pafnuty Chebyshev van contribuir a la teoria de la probabilitat, la majoria de la comunitat matemàtica no va considerar la teoria de la probabilitat com part de les matemàtiques fins al segle XX.

Mecànica estadística

En les ciències físiques, els científics al segle xix van desenvolupar la disciplina de la mecànica estadística, en la que els sistemes físics, com els contenidors plens de gasos, poden considerar-se o tractar-se matemàticament com col·leccions de moltes partícules en moviment. Tot hi que alguns científics, com Rudolf Clausius, van intentar incorporar la aleatorietat a la física estadística, la major part del treball va tenir poca o ninguna aleatorietat. Això va canviar l’any 1859 quan James Clerk Maxwell va contribuir significativament al camp, concretament, a la teoria cinètica dels gasos, al presentar un treball en el que assumia que las partícules de gas es mouen en direccions aleatòries a velocitats aleatòries. La teoria cinètica dels gasos y la física estadística van continuar desenvolupant-se durant la segona meitat del segle xix, amb treballs realitzats principalment per Clausius, Ludwig Boltzmann i Josiah Gibbs, que posteriorment influirien en el model matemàtic de Albert Einstein per al moviment brownià.

Teoria de la mesura i teoria de la probabilitat

En el Congrés Internacional de Matemàtics en Paris l’any 1900, David Hilbert va presentar un llistat de problemes matemàtics on el sisè problema demanava un tractament matemàtic de la física i la probabilitat, que involucrava axiomes. A principis del segle xx, els matemàtics van desenvolupar la teoria de la mesura, una branca de les matemàtiques per estudiar integrals de funcions matemàtiques, on dos dels fundadors van ser matemàtics francesos, Henri Lebesgue i Émile Borel. En 1925, un altre matemàtic francès, Paul Lévy, va publicar el primer llibre de probabilitats que utilitzava idees de la teoria de la mesura.

Durant la dècada de 1920, matemàtics com Sergei Bernstein, Aleksandr Khinchin, i Andrei Kolmogorov van fer contribucions fonamentals a la teoria de la probabilitat en la Unió Soviètica. Kolmogorov en 1929 va publicar el seu primer intent de presentar una base matemàtica basada en la teoria de la mesura per a la teoria de la probabilitat. A principis de la dècada del 1930, Khinchin i Kolmogorov van organitzar seminaris de probabilitat, on investigadors com Eugene Slutsky i Nikolai Smirnov van assistir. Khinchin va donar la primera definició matemàtica d’un procés estocàstic com un conjunt de variables aleatòries indexades per la línia real.

Naixement de la teoria de la probabilitat moderna

L’any 1933, Andrei Kolmogorov va publicar en alemany el seu llibre sobre els fonaments de la teoria de la probabilitat titulat Grundbegriffe der Wahrscheinlichkeitsrechnung, on Kolmogorov va utilitzar la teoria de la mesura per a desenvolupar un marc axiomàtic per a la teoria de la probabilitat. Avui en dia la publicació d’aquest llibre es considera com el naixement de la teoria de la probabilitat moderna, quan les teories de la probabilitat i els processos estocàstics es van convertir en part de les matemàtiques.

Després de la publicació del llibre de Kolmogorov, Khinchi i Kolmogorov, junt amb altres matemàtics com Joseph Doob, William Feller, Maurice Fréchet, Pul Lévy, Wolfgang Döblin i Harald Cramér, van realitzar més treballs fonamentals sobre la teoria de la probabilitat i els processos estocàstics.

Dècades més tard, Cramér es va referir a la dècada del 1930 com el “període heroic de la teoria de la probabilitat matemàtica”. La Segona Guerra Mundial va interrompre en gran manera el desenvolupament de la teoria de la probabilitat, provocant, per exemple, la migració de Feller de Suècia als Estats Units d’Amèrica i la mort de Döblin, ara considerat pioner en processos estocàstics.

Processos estocàstics després de la Segona Guerra Mundial

Després de la Segona Guerra Mundial, l'estudi de la teoria de la probabilitat i els processos estocàstics van guanyar més atenció per part dels matemàtics, amb contribucions significatives realitzades en moltes àrees de probabilitat i matemàtiques, així com la creació de noves àrees. A partir de la dècada del 1940, Kiyosi Itô va publicar articles que desenvolupaven el camp del càlcul estocàstic, que involucra integrals estocàstiques i equacions diferencials estocàstiques basades en el procés de moviment de Wiener o Brownià.

També a partir de la dècada del 1940, es van establir connexions entre els procediments estocàstics, particularment les martingales, i el camp matemàtic de la teoria potencial, amb les primeres idees de Shizuo Kakutani i posteriorment amb el treball de Joseph Doob. Gilbert Hunt va realitzar un treball addicional, considerat pioner, en la dècada del 1950, connectant els processos de Markov i la teoria potencial, el qual va tenir un efecte significatiu en la teoria dels processos de Lévy i va portar a un major interès en el estudi dels processos de Markov amb els mètodes desenvolupats per Itô.

En 1953 Doob va publicar el seu llibre Processos estocàstics, el qual va tenir una forta influencia en la teoria dels processos estocàstics i va destacar la importància de la teoria de la mesura en la probabilitat, Doob també va desenvolupar principalment la teoria de les martingales, amb contribucions substancials posteriors de Paul-André Meyer, Sergei Bernstein, Paul Lévy i Jean Ville que havien realitzat treballs anterior, adoptant aquest últim el terme martingala per al procés estocàstic. Els mètodes de la teoria de les martingales es van popularitzar per a resoldre diferents problemes de probabilitat. Es van desenvolupar tècniques i teories per a estudiar els processos de Markov i després es van aplicar a les martingales. Pel contrari, es van establir mètodes de la teoria de les martingales per a tractar els processos de Markov.

Es van desenvolupar i utilitzar altres camps de probabilitat per a estudiar els processos estocàstics, sent un objectiu principal la teoria de les grans desviacions. La teoria té moltes aplicacions en la física estadística, entre altres camps, i les seves idees centrals es remunten com a mínim a la dècada de 1930. Més tard, en els anys seixanta i setanta, Alexander Wentzell en la Unió Soviètica i Monroe D.Donsker i Srinicasa Varadhan en els Estats Units d’Amèrica van realitzar un treball fonamental pel que més endavant resultaria que Varadhan guanyaria el Premi Abel de 2007. En les dècades de 1990 i 2000, les teories de l'evolució de Schramm-Loewner es van introduir i desenvolupar per a estudiar processos estocàstics i altres àrees matemàtiques en la teoria de la probabilitat, pel que a Wendelin Werner li van entregar les medalles Fields al 2008 i a Martin Harier en 2014, respectivament.

La teoria dels processos estocàstics segueix sent un objectiu de investigació, amb conferències internacionals anuals sobre el tema dels processos estocàstics.

Descobriments de processos estocàstics específics

Tot hi que Khinchin va donar definicions matemàtiques de processos estocàstics en la dècada del 1930, ja s’havien descobert processos estocàstica específics en diferents escenaris, com el procés del moviment browianà o el procés de Poisson. Algunes famílies de processos estocàstics, com els processos puntuals o els processos de renovació, tenen històries llargues i complexes, que es remunten a segles anteriors.

Procés de Bernoulli

El procés de Bernoulli, que pot servir com a model matemàtic per a llençar una moneda esbiaixada, és possiblement el primer procés estocàstic que s’ha estudiat. El procés és una seqüència de assajos independents de Bernoulli, que porten el nom de Jackob Bernoulli, que els va utilitzar per a estudiar els jocs d’atzar, inclosos els problemes de probabilitat proposats i estudiats anteriorment per Christiaan Huygens. El treball de Bernoulli, inclòs el procés de Bernoulli, es va publicar al seu llibre Ars Conjectandi en 1713.

Processos aleatoris

En 1905 Karl Pearson va encunyar el terme caminada aleatòria mentre es plantejava un problema que descrivia una caminada aleatòria en l'avió (que estava motivat per una aplicació en la biologia), però aquesta mena de problemes relacionats amb caminades aleatòries ja s’havien estudiat en altres camps. Certs problemes de joc que es van estudiar segles abans poden considerar-se problemes relacionats com caminades a l’atzar. Per exemple, el problema conegut com la ruïna del jugador es basa en una caminada aleatòria simple, i es un exemple de una caminada aleatòria amb barreres absorbents. Pascal, Fermat i Huyens van donar solucions numèriques a aquest problema sense detallar els seus mètodes. Més endavant, Jakob Bernoulli i Abraham de Moivre van presentar solucions més detallades.

Per a passejos n-dimensionals per gelosies, George Pólya va publicar en 1919 i 1921 treballs on estudiava la probabilitat de una caminada aleatòria simètrica per a tornar a una posició anterior de la xarxa. Pólya va demostrar que una caminada aleatòria simètrica que té la mateixa probabilitat d’avançar en qualsevol direcció en la gelosia, tornarà a una posició anterior en la gelosia un nombre infinit de cops amb probabilitat 1 en una o dos dimensions, però amb probabilitat 0 per a tres o més dimensions.

Procés de Wiener

El procés de Wiener o procés de moviment brownià té els seus orígens en diferents camps, inclosos la estadística, les finances i la física. En 1880, Thorvald Thiele va escriure un article sobre el mètode de mínims quadrats, on va utilitzar el procés per a estudiar els errors de un model en el anàlisi de series del temps. El treball ara es considera un descobriment primerenc del mètode estadístic conegut com filtre de Kalman. Es creu que les idees de l’article de Thiele eren massa avançades per haver sigut enteses per la comunitat matemàtica d’aquell moment.

El matemàtic francés Louis Bachelier va utilitzar en procés de Wiener en la seva tesi del 1900 per a modelar els canvis de preus de la Borsa de Paris, una borsa de valors, sense conèixer el treball de Thiele. S’ha especulat que Bachelier va extreure idees del model de passeig aleatori de Jules Regnault, pero Bachelier no el va citar. La tesis de Bachelier ara es considera pionera en el camp de les matemàtiques financeres.

Es pensa que el treball de Bachelier va guanyar poca atenció i va se oblidat durant dècades fins que va ser redescobert en la dècada del 1950 per Leonard Savage, i es va fer més popular després que la tesis de Bachelier es traduís a l'anglès en 1964. Bachelier va publicar un llibre en 1912 detallen les seves idees, el qual va ser criticat per matemàtics com Doob, Feller i Kolmogorov. El llibre va continuar sent citat, però més tard, a partir de la dècada de 1960, la tesis original de Bachelier va començar a citar-se més que el seu llibre quan els economistes van començar a citar el treball de Bachelier.

En el 1905, Albert Einstein va publicar un article en el que estudiava la observació física del moviment brownià o el moviment per a explicar els moviments aparentment aleatoris de partícules en líquids utilitzant idees de la teoria cinètica dels gasos. Einstein va derivar una equació diferencial, coneguda com equació de difusió, per a escriure la probabilitat de trobar una partícula en una determinada regió de l'espai. Poc més tard del primer article de Einstein sobre el moviment brownià, Marian Smoluchowski va publicar un treball en el que citava a Einstein, però va escriure que havia obtingut de forma independent els resultats equivalents utilitzant un mètode diferent.

El treball de Einstein, així com els resultats experimentals obtinguts per Jean Perrin, van inspirar més endavant a Norbert Wiener en la dècada del 1920 a utilitzar un tipus de teoria de la mesura, desenvolupada per Percy Daniell, i el anàlisi de Fourier per a demostrar la existència del procés de Wiener com un mètode matemàtic.

Procés de Poisson

El procés de Poisson porta el nom de Siméon Poisson, degut a que la seva definició inclou la distribució de Poisson, però Poisson mai va estudiar el procés.

Hi ha una sèrie de afirmacions sobre utilitzacions o descobriments primerencs del procés de Poisson. A principis del segle xx, el procés de Poisson va sorgir de forma independent en diferents situacions. En Suècia el 1903, Filip Lundberg va publicar una tesis ara considerada fonamental i pionera, on proposava modelar las reclamacions d'assegurances amb un procés de Poisson homogeni.

Un altre descobriment va ocórrer en Dinamarca al 1909 quan AK Erlang va derivar la distribució de Poisson al desenvolupar un model matemàtic per al nombre de trucades telefòniques entrants en un interval de temps finit. Erlang no s’havia assabentat en aquell moment del treball anterior de Poisson i va assumir que el nombre de trucades telefòniques que arribaven en cada interval de temps eren independents entre si. Després va trobar el cas límit, que efectivament estava reformulant la distribució de Poisson com un límit de la distribució binomial.

En 1910, Ernest Rutherford i Hans Geiger van publicar resultats experimentals sobre el recompte de partícules alfa. Motivat pel seu treball, Harry Bateman va estudiar el problema de contar i va derivar probabilitats de Poisson com una solució a una família d'equacions diferencials, el que va resultar ajudar en descobriment independent del procés de Poisson. Després van haver molts estudis i aplicacions del procés de Poisson, els quals han estat explicats per a les diverses aplicacions del procés en nombrosos camps per biòlegs, ecòlegs, enginyers i científics físics.^[6]

Procés de Markov

Els processos de Markov i les cadenes de Markov porten el nom de Andrey Markov, qui va estudiar les cadenes de Markov a principis del segle xx. Markov estava interessat en estudiar una extensió de seqüències aleatòries independents. En el seu primer article sobre cadenes de Markov, publicat en 1906, Markov va mostrar que sota certes condicions la mitjana del resultat de la cadena de Markov convergiria a un vector fix de valors, demostrant així una llei dèbil de grans números sense independència, fet que s’havia considerat com un requisit per a que es complissin aquestes lleis matemàtiques. Més endavant, Markov va utilitzar cadenes de Markov per a estudiar la distribució de vocals en Eugene Onegin, escrit per Alexander Pushkin, i va demostrar un teorema de límit central per a les cadenes.

En 1912, Poincaré va estudiar les cadenes de Markov en grups finits amb l’objectiu d'estudiar el barallat de cartes. Altres utilitzacions de les cadenes de Markov, inclouen un model de difusió, introduït per Paul i Tatyana Ehrenfest en 1907, i un procés de ramificació, introduït per Francis Galton i Henry William Watson en 1873, abans del treball de Markov. Després del treball de Galton i Watson, es va revelar que el seu procés de ramificació havia sigut descobert i estudiat de forma independent unes tres dècades abans per Irénée-Jules Bienaymé. A partir de 1928, Maurice Fréchet es va interessar en les cadenes de Markov, el que finalment el va portar a publicar el 1928 un estudi detallat sobre les cadenes de Markov.  

Andrei Kolmogorov va desenvolupar en un article de 1931 una gran part de la teoria inicial dels processos de Markov en temps continu. Kolmogorov es va inspirar en el treball de 1900 de Louis Bachelier sobre les fluctuacions en el mercat de valors, així com en el treball de Norbert Wiener sobre el model de Einstein del moviment brownià. Va introduir i estudiar un conjunt particular de processos de Markov coneguts com processos de difusió, on va derivar un conjunt d'equacions diferencials que descriuen els processos.

Independentment del treball de Kolmogorov, Sydney Chapman va derivar en un article de 1928 una equació, ara nombrada Chapman-Kolmogorov, de una forma menys rigorosa matemàticament que Kolmogorov, mentre estudiava el moviment brownià. Les equacions diferencials ara es denominen equacions de Kolmogorov o equacions de Kolmogorov-Chapman. Altres matemàtics van contribuir significativament als fonaments dels processos de Markov incloent a William Feller, a partir de la dècada del 1930, i després a Eugene Dynkin, a partir de la dècada del 1950.  

Procés de Lévy

Els procés de Lévy com el procés de Wiener i el procés de Poisson (en la línia real) porten el nom de Paul Lévy, qui va començar a estudiar-los en la dècada del 1930, però tenen connexions amb distribucions infinitament divisibles que es remunten a la dècada del 1920. En un article del 1932, Kolmogorov va derivar una funció característica per a les variables aleatòries associades amb els processos de Lévy. Aquest resultat posteriorment va ser derivat en condicions més generals per Lévy al 1934, i després Khinchin va donar de forma independent una forma alternativa per a aquesta funció característica el 1937. A més de Lévy, Khinchin y Kolmogorov, les primeres contribucions fonamentals a la teoria dels processos de Lévy van ser realitzats per Bruno de Finetti i Kiyosi Itô.

Referències

1. «procès estocàstic | enciclopèdia.cat». [Consulta: 18 gener 2022].
2. «Proceso estocástico - Definición, qué es y concepto» (en castellà). [Consulta: 18 gener 2022].
3. Bruguera i Talleda, Jordi; Fluvià i Figueras, Assumpta. «estocàstic». A: Diccionari etimològic. Barcelona: Enciclopèdia Catalana, 1996 (2004, 4a edició), p. 361. ISBN 9788441225169.
4. Dagum, Camilo i Estela M. Bee d'Dagum (1971)Introducció a l'Econometria: 79-83. Mèxic: Siglo XXI editores, setè edició, 1980.
5. Es diu "filtració" a una successió (B (t), t ? T) de sub-s-àlgebres tal que B (t) està inclosa en B (r) si r <t.
6. «stochastic process | mathematics | Britannica» (en anglès). [Consulta: 18 gener 2022].

Vegeu també

• Sistema determinista