Remove ads
গণিত এবং কম্পিউটার বিজ্ঞানের আলোচনায় কলনবিধি বা ইংরেজি ভাষায় অ্যালগরিদম (Algorithm) বলতে একটি সুনির্দিষ্ট পদ্ধতিকে বোঝায়, যেটি কম্পিউটারে বাস্তবায়নযোগ্য ও সুনির্দিষ্ট ক্রমে বিন্যস্ত নির্দেশের সমষ্টি, যে নির্দেশগুলিকে ধাপগুলো অনুসরণ করে কোনও সুসংজ্ঞায়িত পরিগণনামূলক সমস্যার সমাধান করা হয়।[১][২] অন্যভাবে বললে, কলনবিধি বা অ্যালগরিদম হচ্ছে ধাপে ধাপে সমস্যা সমাধানের পদ্ধতি বিশেষ। অর্থাৎ একটি সমস্যাকে সীমিত সংখ্যক কয়েকটি ধাপে ভেঙে প্রত্যেকটি ধাপ পরপর সমাধান করে সমগ্র সমস্যা সমাধান করা হয়। পরিগণক যন্ত্র (কম্পিউটার), রোবট, এমনকি মানুষও কলনবিধি বা অ্যালগরিদমের ধাপগুলি ধারাবাহিকভাবে অনুসরণ করে একটি নির্দিষ্ট কাজ সম্পাদন করতে পারে। পরিগণক বিজ্ঞানের (কম্পিউটার বিজ্ঞান) বিভিন্ন সমস্যা সমাধানের জন্য সঠিক কলনবিধি বা অ্যালগরিদমের ধারণাটি অত্যন্ত গুরুত্বপূর্ণ। কলনবিধি বা অ্যালগরিদমগুলি পরিগণনা (কম্পিউটেশন), উপাত্ত প্রক্রিয়াজাতকরণ (ডেটা প্রসেসিং), স্বয়ংক্রিয় যুক্তি, স্বয়ংক্রিয় সিদ্ধান্ত গ্রহণ এবং অন্যান্য কার্য সম্পাদনের জন্য বিনির্দেশ স্পেসিফিকেশন হিসেবে ব্যবহৃত হয়।
একটি কলনবিধি বা অ্যালগরিদমকে যেকোনও ভাষায় বর্ণনা করা যেতে পারে, সে ভাষাটি হতে পারে বাংলা, ইংরেজির মত মানুষের মৌখিক ভাষা,অথবা সি++ , এইচটিএমএল, এইচটিএমএল ৫, সিএসএস , পাইথন , সি , সি শার্প , গো , রুবি , জুলিয়া জাভার মত প্রোগ্রাম (পূর্বলিখিত নির্দেশক্রম) রচনার ভাষা। এমনকি যন্ত্রাংশসামগ্রী (হার্ডওয়্যার) নকশাকরণের মাধ্যমেও এটি বর্ণনা করা যেতে পারে। তবে যে ভাষাতেই লেখা হোক না, সমস্যা সমাধানের প্রতিটি ধাপের বর্ণনা কলনবিধি বা অ্যালগরিদমে থাকতে হবে।
পরিগণক বিজ্ঞান তথা কম্পিউটার বিজ্ঞানের সমস্ত ক্ষেত্রে যেমন উপাত্তাধার (ডেটাবেজ), চিত্রলিখন (গ্রাফিক্স), জালিকায়ন (কম্পিউটার নেটওয়ার্কিং), পরিচালক ব্যবস্থা (অপারেটিং সিস্টেম), কম্পিউটার নিরাপত্তা, কৃত্রিম বুদ্ধিমত্তা, ইত্যাদিতে কলনবিধি বা অ্যালগরিদম নির্মাণ ও বিশ্লেষণ একটি মৌলিক কর্মকাণ্ড। অ্যালগরিদম নির্মাণ এবং প্রোগ্রাম (পূর্বলিখিত নির্দেশক্রম) রচনার মধ্যে পার্থক্য আছে। কলনবিধি বা অ্যালগরিদম নির্মাণের সময় কোনও পরিগণনামূলক সমস্যা সমাধানের উদ্দেশ্যে লভ্য সমস্ত বিকল্প ঠিকমতো বোঝা অত্যাবশ্যক। অর্থাৎ কোনও নির্দিষ্ট সমাধানের জন্য কী যন্ত্রাংশসামগ্রী (হার্ডওয়্যার) ব্যবহৃত হবে, নেটওয়ার্ক তথা জালিকাব্যবস্থাটি কী রকম, কোন্ ভাষায় প্রোগ্রাম রচিত হবে, কর্মদক্ষতার উপরে কী কী সীমাবদ্ধতা বিদ্যমান, এই সব কিছু বিবেচনায় রাখতে হয়। কোনও অ্যালগরিদম যদি কোনও সমস্যাকে পূর্ণাঙ্গরূপে এবং দক্ষভাবে সমাধান করতে পারে, তাহলে সেটিকে "সঠিক" বিবেচনা করা হয়। অ্যালগরিদমগুলি প্রবিষ্ট উপাত্ত (ইনপুট) ও বহির্গত উপাত্তের (আউটপুট) মাধ্যমে কাজ করে। প্রবিষ্ট উপাত্তের উপরে কলনবিধি বা অ্যালগরিদমের প্রতিটি ধাপ ধারাবাহিকভাবে প্রয়োগ করা হয় এবং সবশেষে বহির্গত উপাত্ত ফলাফল হিসেবে প্রকাশিত হয়। একটি কলনবিধি বা অ্যালগরিদমকে তখনই "সঠিক" বলা হয় যদি প্রতিটি প্রবিষ্ট উপাত্তের জন্য কলনবিধি বা অ্যালগরিদমটি সঠিক বহির্গত উপাত্ত উৎপাদন করে। তবে পুরোপুরি নির্ভুল নয় এমন কলনবিধি বা অ্যালগরিদমও গুরুত্বপূর্ণ হতে পারে, যদি ভুলের মাত্রা নিয়ন্ত্রণের মধ্যে রাখা যায়।
ইংরেজি "অ্যালগরিদম" শব্দটি ৯ম শতাব্দীর মুসলিম গণিতবিদ মুসা আল খোয়ারিজমি-র নাম থেকে এসেছে।[৩][৪][৫]
কলনবিধি বা অ্যালগরিদমের বিপরীত ধারণাটি হল আবিষ্করণী পদ্ধতি (Heuristic-হিউরিস্টিক), যা হল অতীত অভিজ্ঞতার মূল্যায়নের নিরিখে প্রয়াস ও প্রমাদের (trial and error) মধ্য দিয়ে আরোহী যুক্তিবিন্যাসের মাধ্যমে সমস্যা সমাধানের একটি পদ্ধতি; এটি সম্পূর্ণরূপে নির্দিষ্ট না-ও হতে পারে কিংবা সঠিক বা সর্বোত্তম ফলাফলের নিশ্চয়তা না-ও দিতে পারে (বিশেষ করে সেইসব সমস্যাক্ষেত্রে যেখানে কোন সুনির্দিষ্ট সঠিক বা সর্বোত্তম ফলাফল নেই)।[৬]
Remove ads
 | এই পরিচ্ছেদটি অন্য একটি ভাষা থেকে আনাড়িভাবে অনুবাদ করা হয়েছে। এটি কোনো কম্পিউটার অথবা দ্বিভাষিক দক্ষতাহীন কোনো অনুবাদক অনুবাদ করে থাকতে পারেন। |
অ্যালগরিদমের ধারণাটি প্রাচীনকাল থেকেই বিদ্যমান। পাটিগণিত অ্যালগরিদম, যেমন একটি বিভাগ অ্যালগরিদম, প্রাচীন ব্যাবিলনীয় গণিতবিদরা ব্যবহার করতেন c. 2500 BC এবং মিশরীয় গণিতবিদ গ. ১৫৫০ খ্রিস্টপূর্বাব্দ। [৭] গ্রীক গণিতবিদরা পরবর্তীতে ২৪০ খ্রিস্টপূর্বাব্দে মৌলিক সংখ্যা খুঁজে বের করার জন্য ইরাটোস্থেনিসের চালুনিতে অ্যালগরিদম এবং দুটি সংখ্যার সর্বশ্রেষ্ঠ সাধারণ ভাজক খুঁজে বের করার জন্য ইউক্লিডীয় অ্যালগরিদম ব্যবহার করেন। [৮] ৯ম শতাব্দীতে আল-কিন্দির মতো আরবি গণিতবিদরা ফ্রিকোয়েন্সি বিশ্লেষণের ভিত্তিতে কোড-ব্রেকিংয়ের জন্য ক্রিপ্টোগ্রাফিক অ্যালগরিদম ব্যবহার করতেন। [৯]
অ্যালগরিদম শব্দটি ৯ম শতাব্দীর ফার্সি গণিতবিদ মুহম্মদ ইবনে মুসা আল-খোয়ারিজমির নাম থেকে এসেছে, যার নিসবা (তাঁকে খোয়ারজম থেকে চিহ্নিত করা হয়েছে) ল্যাটিন করা হয়েছিল আলগোরিত্মি ( আরবাইজড ফার্সি الخوارزمی c. 780-780)। [১০][১১] মুহাম্মাদ ইবনে মুসা আল-খোয়ারিজমি ছিলেন একজন গণিতবিদ, জ্যোতির্বিদ, ভূগোলবিদ এবং বাগদাদের হাউস অফ উইজডমের পণ্ডিত, যার নামের অর্থ ' খোয়ারজমের স্থানীয়', এমন একটি অঞ্চল যা বৃহত্তর ইরানের অংশ ছিল এবং এখন উজবেকিস্তানে রয়েছে। [১২][১৩] প্রায় ৮২৫, আল-খোয়ারিজমি হিন্দু-আরবি সংখ্যা পদ্ধতির উপর একটি আরবি ভাষার গ্রন্থ লিখেছিলেন, যা ১২ শতকে ল্যাটিন ভাষায় অনুবাদ করা হয়েছিল। পাণ্ডুলিপিটি শুরু হয় দীক্ষিত আলগোরিজমি ('এইভাবে আল-খোয়ারিজমি') বাক্যাংশ দিয়ে, যেখানে "আলগোরিজমি" ছিল অনুবাদকের আল- খোরিজমির নামের ল্যাটিনাইজেশন। [১৪] আল-খোয়ারিজমি ছিলেন মধ্যযুগের শেষের দিকে ইউরোপে সর্বাধিক পঠিত গণিতবিদ, প্রাথমিকভাবে তার অন্য একটি বইয়ের মাধ্যমে, বীজগণিতের মাধ্যমে। মধ্যযুগের শেষের দিকে ল্যাটিন, অ্যালগোরিসমাস, ইংরেজি ' অ্যালগোরিজম ', তার নামের অপভ্রংশ, কেবল "দশমিক সংখ্যা পদ্ধতি" বোঝায়। ১৫ শতকে, গ্রিক শব্দ ἀριθμός ( arithmos ), 'সংখ্যা' ( cf. 'পাটিগণিত') এর প্রভাবে, ল্যাটিন শব্দটি অ্যালগরিদমাসে পরিবর্তিত হয়েছিল, এবং সংশ্লিষ্ট ইংরেজি শব্দ 'অ্যালগরিদম' প্রথম ১৭ তম সালে প্রমাণিত হয় শতাব্দী; আধুনিক অর্থ ১৯ শতকে প্রবর্তিত হয়েছিল। [১৫]
ভারতীয় গণিত প্রধানত অ্যালগরিদমিক ছিল। অ্যালগরিদমগুলি প্রাচীন থেকে ভারতীয় গাণিতিক ঐতিহ্যের প্রতিনিধিত্ব করে শুলবাসূত্র থেকে কেরালা স্কুলের মধ্যযুগীয় পাঠ্য পর্যন্ত।[তথ্যসূত্র প্রয়োজন]
ইংরেজিতে, অ্যালগরিদম শব্দটি প্রথম ব্যবহৃত হয়েছিল প্রায় 1230 সালে এবং তারপর চসার দ্বারা ১৩৯১ সালে। ইংরেজি ফরাসি শব্দটি গ্রহণ করেছিল, কিন্তু ১৯ শতকের শেষের দিকে "অ্যালগরিদম" আধুনিক ইংরেজিতে যে অর্থ রয়েছে তা গ্রহণ করেনি। [১৬]
আলেকজান্দ্রে দে ভিলেদিউ দ্বারা রচিত কারমেন ডি অ্যালগোরিসমো শিরোনামের একটি ম্যানুয়ালটিতে ১২৪০ সাল থেকে শব্দের আরেকটি প্রাথমিক ব্যবহার। এটি দিয়ে শুরু হয়:
এই বর্তমান শিল্প, যেখানে আমরা সেই দ্বিগুণ পাঁচটি ভারতীয় চিত্র ব্যবহার করি, তাকে অ্যালগোরিসমাস বলা হয়।
এই বর্তমান শিল্প, যেখানে আমরা সেই দ্বিগুণ পাঁচটি ভারতীয় চিত্র ব্যবহার করি, তাকে অ্যালগোরিসমাস বলা হয়।
যা অনুবাদ করে: অ্যালগরিদম হল সেই শিল্প যার দ্বারা বর্তমানে আমরা সেই ভারতীয় পরিসংখ্যানগুলি ব্যবহার করি, যা দুই বার পাঁচ নম্বর। কবিতাটি কয়েকশত লাইন দীর্ঘ এবং নতুন শৈলীকৃত ভারতীয় পাশা (টালি ইন্ডোরাম), বা হিন্দু সংখ্যার সাথে গণনার শিল্পকে সংক্ষিপ্ত করে। [১৭]
অ্যালগরিদমের আধুনিক ধারণার একটি আংশিক আনুষ্ঠানিকীকরণ 1928 সালে ডেভিড হিলবার্ট দ্বারা উত্থাপিত Entscheidungsproblem (সিদ্ধান্ত সমস্যা) সমাধানের প্রচেষ্টার মাধ্যমে শুরু হয়েছিল। " কার্যকর গণনাযোগ্যতা " [১৮] বা "কার্যকর পদ্ধতি" সংজ্ঞায়িত করার প্রচেষ্টা হিসাবে তৈরি করা হয়েছিল। [১৯] এই ফর্মালাইজেশনগুলির মধ্যে 1930, 1934 এবং 1935 সালের Gödel – Herbrand – Kleene রিকার্সিভ ফাংশন, 1936 সালের অ্যালোঞ্জো চার্চের ল্যাম্বডা ক্যালকুলাস, 1936 সালের এমিল পোস্টের ফর্মুলেশন 1 এবং অ্যালান টুরিং -এর টুরিং মেশিন 1936–37 এবং 1936-এর অন্তর্ভুক্ত ছিল।
Remove ads
| এই পরিচ্ছেদটি অন্য একটি ভাষা থেকে আনাড়িভাবে অনুবাদ করা হয়েছে। এটি কোনো কম্পিউটার অথবা দ্বিভাষিক দক্ষতাহীন কোনো অনুবাদক অনুবাদ করে থাকতে পারেন। |
একটি অনানুষ্ঠানিক সংজ্ঞা হতে পারে "নিয়মের একটি সেট যা সঠিকভাবে ক্রিয়াকলাপের একটি ক্রমকে সংজ্ঞায়িত করে",[২০][যাচাই করার জন্য উদ্ধৃতি প্রয়োজন] যার মধ্যে সমস্ত কম্পিউটার প্রোগ্রাম অন্তর্ভুক্ত থাকবে (এমন প্রোগ্রামগুলি যা সাংখ্যিক গণনা করে না) এবং (উদাহরণস্বরূপ) যেকোন নির্ধারিত আমলাতান্ত্রিক পদ্ধতি [২১] বা রান্নার বইয়ের রেসিপি । [২২]
সাধারণভাবে, একটি প্রোগ্রাম শুধুমাত্র একটি অ্যালগরিদম হয় যদি এটি শেষ পর্যন্ত থেমে যায় [২৩] — যদিও অসীম লুপ কখনও কখনও পছন্দসই প্রমাণিত হতে পারে।
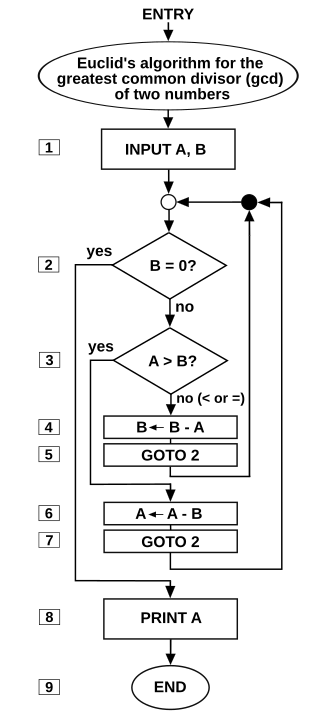
একটি অ্যালগরিদমের একটি নমুনা উদাহরণ হল ইউক্লিডীয় অ্যালগরিদম, যা দুটি পূর্ণসংখ্যার সর্বাধিক সাধারণ ভাজক নির্ধারণ করতে ব্যবহৃত হয়; একটি উদাহরণ (অন্যও আছে) উপরের ফ্লোচার্ট দ্বারা এবং পরবর্তী বিভাগে একটি উদাহরণ হিসাবে বর্ণনা করা হয়েছে।
বুলোস & জেফরি (1974, 1999) নিম্নলিখিত উদ্ধৃতিতে "অ্যালগরিদম" শব্দের একটি অনানুষ্ঠানিক অর্থ প্রদান করে:
কোন মানুষই যথেষ্ট দ্রুত, বা যথেষ্ট দীর্ঘ, বা যথেষ্ট ছোট লিখতে পারে না † ( †" ছোট এবং ছোট সীমাহীন... আপনি অণুর উপর, পরমাণুর উপর, ইলেকট্রনের উপর লেখার চেষ্টা করবেন") একটি এর সমস্ত সদস্য তালিকাভুক্ত করতে একের পর এক, কিছু স্বরলিপিতে তাদের নাম লিখে অসংখ্য অসীম সেট। কিন্তু মানুষ সমানভাবে কার্যকর কিছু করতে পারে, নির্দিষ্ট সংখ্যক অসীম সেটের ক্ষেত্রে: তারা নির্বিচারে সসীম n-এর জন্য সেটের nম সদস্য নির্ধারণের জন্য সুস্পষ্ট নির্দেশনা দিতে পারে। এই ধরনের নির্দেশগুলি বেশ স্পষ্টভাবে দেওয়া উচিত, এমন একটি ফর্ম যাতে সেগুলি একটি কম্পিউটিং মেশিন দ্বারা অনুসরণ করা যেতে পারে, অথবা এমন একজন মানুষ যিনি প্রতীকগুলিতে শুধুমাত্র খুব প্রাথমিক ক্রিয়াকলাপগুলি চালাতে সক্ষম। [২৪]
একটি "সংখ্যাযোগ্যভাবে অসীম সেট" হল এমন একটি যার উপাদানগুলিকে পূর্ণসংখ্যার সাথে এক থেকে এক চিঠিপত্রে রাখা যেতে পারে। এইভাবে বুলোস এবং জেফরি বলছেন যে একটি অ্যালগরিদম এমন একটি প্রক্রিয়ার নির্দেশনা বোঝায় যা একটি নির্বিচারে "ইনপুট" পূর্ণসংখ্যা বা পূর্ণসংখ্যা থেকে আউটপুট পূর্ণসংখ্যা "তৈরি করে" যা তত্ত্বগতভাবে, ইচ্ছামত বড় হতে পারে। উদাহরণস্বরূপ, একটি অ্যালগরিদম একটি বীজগণিত সমীকরণ হতে পারে যেমন y = m + n (অর্থাৎ, দুটি নির্বিচারে "ইনপুট ভেরিয়েবল" m এবং n যা একটি আউটপুট y তৈরি করে), কিন্তু ধারণাটিকে সংজ্ঞায়িত করার জন্য বিভিন্ন লেখকের প্রচেষ্টা নির্দেশ করে যে শব্দটি বোঝায় এর থেকে অনেক বেশি, কিছুর অর্ডারে (সংযোজন উদাহরণের জন্য):
- একটি দ্রুত, দক্ষ, "ভাল" প্রক্রিয়ার জন্য সুনির্দিষ্ট নির্দেশাবলী (একটি ভাষায় যা "কম্পিউটার" দ্বারা বোঝা যায়) [২৫] একটি দ্রুত, দক্ষ, "ভাল" [২৬] প্রক্রিয়ার জন্য যা "কম্পিউটার" (মেশিন বা মানব, অভ্যন্তরীণভাবে প্রয়োজনীয় সজ্জিত) এর "চালগুলি" নির্দিষ্ট করে, তথ্য এবং ক্ষমতা রয়েছে) [২৭] খুঁজে বের করতে, ডিকোড করতে এবং তারপরে নির্বিচারে ইনপুট পূর্ণসংখ্যা/প্রতীক m এবং n, চিহ্ন + এবং = ... এবং "কার্যকরভাবে" [২৮] প্রসেস করতে, একটি "যুক্তিসঙ্গত" সময়ে,[২৯] আউটপুট-পূর্ণসংখ্যা y একটি নির্দিষ্ট জায়গায় এবং একটি নির্দিষ্ট বিন্যাসে।
অ্যালগরিদমের ধারণাটি সিদ্ধান্তযোগ্যতার ধারণাকে সংজ্ঞায়িত করার জন্যও ব্যবহৃত হয় - একটি ধারণা যা একটি স্বতঃসিদ্ধ এবং নিয়মের একটি ছোট সেট থেকে আনুষ্ঠানিক সিস্টেমগুলি কীভাবে তৈরি হয় তা ব্যাখ্যা করার জন্য কেন্দ্রীয়। যুক্তিতে, একটি অ্যালগরিদম সম্পূর্ণ করার জন্য যে সময় প্রয়োজন তা পরিমাপ করা যায় না, কারণ এটি দৃশ্যত প্রথাগত শারীরিক মাত্রার সাথে সম্পর্কিত নয়।এই ধরনের অনিশ্চয়তা থেকে, যা চলমান কাজকে চিহ্নিত করে, অ্যালগরিদমের একটি সংজ্ঞার অনুপলব্ধতা তৈরি করে যা কংক্রিট (কিছু অর্থে) এবং শব্দটির বিমূর্ত ব্যবহার উভয়ের জন্য উপযুক্ত।
বেশিরভাগ অ্যালগরিদম কম্পিউটার প্রোগ্রাম হিসাবে প্রয়োগ করার উদ্দেশ্যে করা হয়। যাইহোক, অ্যালগরিদমগুলি অন্যান্য উপায়ে প্রয়োগ করা হয়, যেমন একটি জৈবিক নিউরাল নেটওয়ার্কে (উদাহরণস্বরূপ, মানব মস্তিষ্ক গাণিতিক প্রয়োগ করে বা খাদ্যের সন্ধানে একটি পোকা), বৈদ্যুতিক সার্কিটে বা একটি যান্ত্রিক যন্ত্রে।
Remove ads
| এই পরিচ্ছেদটি অন্য একটি ভাষা থেকে আনাড়িভাবে অনুবাদ করা হয়েছে। এটি কোনো কম্পিউটার অথবা দ্বিভাষিক দক্ষতাহীন কোনো অনুবাদক অনুবাদ করে থাকতে পারেন। |
কম্পিউটার যেভাবে ডেটা প্রসেস করে তার জন্য অ্যালগরিদম অপরিহার্য। অনেক কম্পিউটার প্রোগ্রামে অ্যালগরিদম থাকে যা একটি নির্দিষ্ট কাজ সম্পাদন করার জন্য, যেমন কর্মচারীদের বেতন চেক গণনা করা বা ছাত্রদের রিপোর্ট কার্ড মুদ্রণ করার জন্য - একটি নির্দিষ্ট ক্রমে - একটি কম্পিউটারের যে নির্দিষ্ট নির্দেশাবলী সম্পাদন করা উচিত তার বিশদ বিবরণ। এইভাবে, একটি অ্যালগরিদমকে ক্রিয়াকলাপের যেকোন ক্রম হিসাবে বিবেচনা করা যেতে পারে যা একটি টুরিং-সম্পূর্ণ সিস্টেম দ্বারা অনুকরণ করা যেতে পারে। যে লেখকরা এই থিসিসটি দাবি করেছেন তাদের মধ্যে রয়েছে মিনস্কি (1967), স্যাভেজ (1987) এবং গুরেভিচ (2000):
মিনস্কি: "তবে আমরা টিউরিংয়ের সাথেও বজায় রাখব... যে কোনও পদ্ধতি যাকে "স্বাভাবিকভাবে" কার্যকর বলা যেতে পারে, বাস্তবে একটি (সরল) মেশিন দ্বারা উপলব্ধি করা যেতে পারে। যদিও এটি চরম মনে হতে পারে, যুক্তিগুলি ... এর পক্ষে খণ্ডন করা কঠিন" [৩০] গুরেভিচ: "... তার থিসিসের পক্ষে টুরিংয়ের অনানুষ্ঠানিক যুক্তি একটি শক্তিশালী থিসিসকে ন্যায্যতা দেয়: প্রতিটি অ্যালগরিদম একটি টুরিং মেশিন দ্বারা অনুকরণ করা যেতে পারে … স্যাভেজ [1987] অনুসারে, একটি অ্যালগরিদম হল একটি টুরিং মেশিন দ্বারা সংজ্ঞায়িত একটি গণনামূলক প্রক্রিয়া"। [৩১]
টিউরিং মেশিন গণনামূলক প্রক্রিয়াগুলিকে সংজ্ঞায়িত করতে পারে যা শেষ হয় না। অ্যালগরিদমগুলির অনানুষ্ঠানিক সংজ্ঞাগুলির জন্য সাধারণত অ্যালগরিদমটি সর্বদা বন্ধ করা প্রয়োজন। এই প্রয়োজনীয়তাটি একটি আনুষ্ঠানিক পদ্ধতি একটি অ্যালগরিদম যা সাধারণ ক্ষেত্রে অসম্ভব কিনা তা সিদ্ধান্ত নেওয়ার কাজটি রেন্ডার করে - কম্পিউটেবিলিটি তত্ত্বের একটি প্রধান উপপাদ্য যা থামানো সমস্যা হিসাবে পরিচিত।
সাধারণত, যখন একটি অ্যালগরিদম তথ্য প্রক্রিয়াকরণের সাথে যুক্ত থাকে, তখন তথ্য একটি ইনপুট উত্স থেকে পড়া যায়, একটি আউটপুট ডিভাইসে লেখা হয় এবং পরবর্তী প্রক্রিয়াকরণের জন্য সংরক্ষণ করা যায়। সঞ্চিত ডেটা অ্যালগরিদম সম্পাদনকারী সত্তার অভ্যন্তরীণ অবস্থার অংশ হিসাবে বিবেচিত হয়। বাস্তবে, রাষ্ট্র এক বা একাধিক ডেটা স্ট্রাকচারে সংরক্ষণ করা হয়।
এই গণনামূলক প্রক্রিয়াগুলির কিছুর জন্য, অ্যালগরিদমকে অবশ্যই কঠোরভাবে সংজ্ঞায়িত করতে হবে: উদ্ভূত সমস্ত সম্ভাব্য পরিস্থিতিতে এটি যেভাবে প্রযোজ্য তা নির্দিষ্ট করে। এর মানে হল যে কোন শর্তসাপেক্ষ পদক্ষেপগুলি অবশ্যই পদ্ধতিগতভাবে মোকাবেলা করতে হবে, কেস-বাই-কেস; প্রতিটি ক্ষেত্রের মানদণ্ড অবশ্যই পরিষ্কার (এবং গণনাযোগ্য) হতে হবে।
যেহেতু একটি অ্যালগরিদম হল সুনির্দিষ্ট পদক্ষেপের একটি সুনির্দিষ্ট তালিকা, তাই অ্যালগরিদমের কার্যকারিতার জন্য গণনার ক্রম সর্বদা গুরুত্বপূর্ণ। নির্দেশাবলী সাধারণত সুস্পষ্টভাবে তালিকাভুক্ত বলে ধরে নেওয়া হয়, এবং "উপর থেকে" শুরু করা এবং "নীচে নীচে" যাওয়া হিসাবে বর্ণনা করা হয় - একটি ধারণা যা নিয়ন্ত্রণের প্রবাহ দ্বারা আরও আনুষ্ঠানিকভাবে বর্ণনা করা হয়।
এখনও অবধি, একটি অ্যালগরিদমের আনুষ্ঠানিককরণের আলোচনাটি অপরিহার্য প্রোগ্রামিংয়ের প্রাঙ্গনে ধরে নিয়েছে। এটি সবচেয়ে সাধারণ ধারণা - যা একটি কাজকে বিচ্ছিন্নভাবে বর্ণনা করার চেষ্টা করে, "যান্ত্রিক" মানে। আনুষ্ঠানিক অ্যালগরিদমের এই ধারণার জন্য অনন্য হল অ্যাসাইনমেন্ট অপারেশন, যা একটি পরিবর্তনশীলের মান নির্ধারণ করে। এটি একটি স্ক্র্যাচপ্যাড হিসাবে " মেমরি " এর অন্তর্দৃষ্টি থেকে উদ্ভূত। এই ধরনের একটি নিয়োগের উদাহরণ নিচে পাওয়া যাবে।
একটি অ্যালগরিদম কী গঠন করে তার কিছু বিকল্প ধারণার জন্য, কার্যকরী প্রোগ্রামিং এবং লজিক প্রোগ্রামিং দেখুন।
Remove ads
| এই পরিচ্ছেদটি অন্য একটি ভাষা থেকে আনাড়িভাবে অনুবাদ করা হয়েছে। এটি কোনো কম্পিউটার অথবা দ্বিভাষিক দক্ষতাহীন কোনো অনুবাদক অনুবাদ করে থাকতে পারেন। |
অ্যালগরিদমগুলি প্রাকৃতিক ভাষা, সিউডোকোড, ফ্লোচার্ট, ড্রাকন-চার্ট, প্রোগ্রামিং ভাষা বা নিয়ন্ত্রণ টেবিল (দোভাষীদের দ্বারা প্রক্রিয়াকৃত) সহ অনেক ধরনের স্বরলিপিতে প্রকাশ করা যেতে পারে। অ্যালগরিদমগুলির প্রাকৃতিক ভাষার অভিব্যক্তিগুলি ভার্বস এবং অস্পষ্ট হতে থাকে এবং জটিল বা প্রযুক্তিগত অ্যালগরিদমের জন্য খুব কমই ব্যবহৃত হয়। সিউডোকোড, ফ্লোচার্ট, ড্রাকন-চার্ট এবং কন্ট্রোল টেবিল হল অ্যালগরিদম প্রকাশ করার কাঠামোগত উপায় যা প্রাকৃতিক ভাষার উপর ভিত্তি করে বিবৃতিতে প্রচলিত অনেক অস্পষ্টতা এড়িয়ে যায়। প্রোগ্রামিং ভাষাগুলি প্রাথমিকভাবে অ্যালগরিদমগুলিকে এমন আকারে প্রকাশ করার উদ্দেশ্যে তৈরি করা হয় যা একটি কম্পিউটার দ্বারা কার্যকর করা যেতে পারে, তবে প্রায়শই অ্যালগরিদমগুলিকে সংজ্ঞায়িত বা নথিভুক্ত করার উপায় হিসাবেও ব্যবহৃত হয়।
বিভিন্ন ধরনের উপস্থাপনা সম্ভব এবং কেউ একটি প্রদত্ত টিউরিং মেশিন প্রোগ্রামকে মেশিন টেবিলের ক্রম হিসাবে প্রকাশ করতে পারে (দেখুন সীমিত-রাষ্ট্র মেশিন, রাষ্ট্রীয় রূপান্তর সারণী এবং আরও জন্য নিয়ন্ত্রণ টেবিল ), ফ্লোচার্ট এবং ড্রাকন-চার্ট হিসাবে (স্টেট ডায়াগ্রাম দেখুন আরও কিছুর জন্য), অথবা প্রাথমিক মেশিন কোড বা অ্যাসেম্বলি কোডের একটি ফর্ম হিসাবে যাকে বলা হয় "চতুষ্পদগুলির সেট" (আরো জন্য টুরিং মেশিন দেখুন)।
অ্যালগরিদমগুলির উপস্থাপনাগুলিকে টিউরিং মেশিনের বর্ণনার তিনটি স্বীকৃত স্তরে শ্রেণীবদ্ধ করা যেতে পারে, নিম্নরূপ:[৩২]
- ১ উচ্চ-স্তরের বর্ণনা
- "...গদ্য একটি অ্যালগরিদম বর্ণনা করার জন্য, বাস্তবায়নের বিবরণ উপেক্ষা করে। এই স্তরে, মেশিনটি কীভাবে তার টেপ বা মাথা পরিচালনা করে তা আমাদের উল্লেখ করার দরকার নেই।"
- ২ বাস্তবায়নের বিবরণ
- "...গদ্য টিউরিং মেশিন কীভাবে তার মাথা ব্যবহার করে এবং কীভাবে এটি তার টেপে ডেটা সংরক্ষণ করে তা সংজ্ঞায়িত করতে ব্যবহৃত হয়। এই স্তরে, আমরা রাজ্য বা রূপান্তর ফাংশনের বিশদ বিবরণ দিই না।"
- ৩ আনুষ্ঠানিক বিবরণ
- সবচেয়ে বিস্তারিত, "সর্বনিম্ন স্তর", টিউরিং মেশিনের "স্টেট টেবিল" দেয়।
তিনটি স্তরে বর্ণিত সহজ অ্যালগরিদম "অ্যাড m+n" এর উদাহরণের জন্য, উদাহরণ দেখুন।
Remove ads
| এই পরিচ্ছেদটি অন্য একটি ভাষা থেকে আনাড়িভাবে অনুবাদ করা হয়েছে। এটি কোনো কম্পিউটার অথবা দ্বিভাষিক দক্ষতাহীন কোনো অনুবাদক অনুবাদ করে থাকতে পারেন। |
অ্যালগরিদম ডিজাইন বলতে সমস্যা সমাধান এবং ইঞ্জিনিয়ারিং অ্যালগরিদমের জন্য একটি পদ্ধতি বা গাণিতিক প্রক্রিয়া বোঝায়। অ্যালগরিদমের নকশা অপারেশন গবেষণার অনেক সমাধান তত্ত্বের অংশ, যেমন ডায়নামিক প্রোগ্রামিং এবং ডিভাইড-এন্ড-কনকার । অ্যালগরিদম ডিজাইন ডিজাইন এবং বাস্তবায়নের কৌশলগুলিকে অ্যালগরিদম ডিজাইন প্যাটার্নও বলা হয়, উদাহরণ সহ টেমপ্লেট পদ্ধতি প্যাটার্ন এবং ডেকোরেটর প্যাটার্ন।
অ্যালগরিদম ডিজাইনের সবচেয়ে গুরুত্বপূর্ণ দিকগুলির মধ্যে একটি হল সম্পদ (রান-টাইম, মেমরি ব্যবহার) দক্ষতা; বড় ও স্বরলিপি ব্যবহার করা হয় যেমন একটি অ্যালগরিদমের রান-টাইম বৃদ্ধির বর্ণনা দিতে, কারণ এটির ইনপুটের আকার বৃদ্ধি পায়।
অ্যালগরিদমগুলির বিকাশের সাধারণ পদক্ষেপগুলি:
- সমস্যার সংজ্ঞা
- একটি মডেলের উন্নয়ন
- অ্যালগরিদমের স্পেসিফিকেশন
- একটি অ্যালগরিদম ডিজাইন করা
- অ্যালগরিদমের সঠিকতা পরীক্ষা করা হচ্ছে
- অ্যালগরিদম বিশ্লেষণ
- অ্যালগরিদম বাস্তবায়ন
- প্রোগ্রাম পরীক্ষা ও
- ডকুমেন্টেশন প্রস্তুতি[স্পষ্টকরণ প্রয়োজন]
Remove ads
Wikiwand in your browser!
Seamless Wikipedia browsing. On steroids.
Every time you click a link to Wikipedia, Wiktionary or Wikiquote in your browser's search results, it will show the modern Wikiwand interface.
Wikiwand extension is a five stars, simple, with minimum permission required to keep your browsing private, safe and transparent.
Remove ads