Hipérbola

Una hipérbola (del griegu ὑπερβολή) ye una seición cónica, una curva abierta de dos rames llograda cortando un conu rectu por un planu oblicuu a la exa de simetría, y con ángulu menor que'l de la generatriz respectu de la exa de revolución.^[1]

Una hipérbola ye'l llugar xeométricu de los puntos d'un planu tales que'l valor absolutu de la diferencia de les sos distancies a dos puntos fixos, llamaos focos, ye igual a la distancia ente los vértices, que ye una constante positiva.

Hipérbola
non-degenerate conic section (en) y sinusoidal spiral (en)

Les asíntotas de la hipérbola amuésense como llinies discontinues azules que se corten nel centru de la hipérbola (curves coloraes), C. Los dos puntos focales denominar F₁ y F₂, la llinia negra que xune los vértices ye la exa tresversal. La delgada llinia perpendicular en negru que pasa pel centru ye la exa conxugada. Les dos llinies grueses en negru paraleles a la exa conxugada (poro, perpendicular a la exa tresversal) son los dos directrices, D₁ y D₂. La escentricidá y (y>1), ye igual al cociente ente les distancies (en verde) dende un puntu P de la hipérbola a unu de los focos y la so correspondiente directriz. Los dos vértices atópase na exa tresversal a una distancia ±a con respectu al centru.

Etimoloxía. Hipérbole ya hipérbola

Seiciones cóniques.

Hipérbola deriva de la pallabra griega ὑπερβολή (escesu), y ye cognáu de hipérbole (la figura lliteraria qu'equival a desaxeración).

Historia

Por cuenta de l'enclín de la corte, el planu de la hipérbola interseca dambes cañes del conu.

Según la tradición, les seiciones cóniques fueron afayaes por Menecmo, nel so estudiu del problema de la duplicación del cubu,^[2] onde demuestra la esistencia d'una solución por aciu la corte d'una parábola con una hipérbola, lo cual ye confirmáu darréu por Proclo y Eratóstenes.^[3]

Sicasí, el primeru n'usar el términu hipérbola foi Apolonio de Perge nel so tratáu Cóniques,^[4] considerada obra cume sobre la tema de les matemátiques griegues, y onde se desenvuelve l'estudiu de les tanxentes a seiciones cóniques.

Ecuaciones de la hipérbola

Ecuaciones en coordenaes cartesianes: Ecuación d'una hipérbola con centru nel orixe de coordenaes ${\displaystyle (0,0)\,}$ y ecuación de la hipérbola na so forma canónica.

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$

Ecuación d'una hipérbola con centru nel puntu ${\displaystyle (h,k)\,}$

${\displaystyle {\frac {(x-h)^{2}}{a^{2}}}-{\frac {(y-k)^{2}}{b^{2}}}=1}$

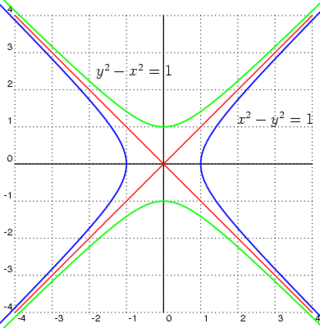
Exemplos:

a)

${\displaystyle {\frac {(x)^{2}}{25}}-{\frac {(y)^{2}}{9}}=1}$

b)

${\displaystyle {\frac {(y)^{2}}{9}}-{\frac {(x)^{2}}{25}}=1}$

Si la exa x ye positivu, entós la hipérbola ye horizontal; si ye al aviesu, ye vertical. La escentricidá d'una hipérbola siempres ye mayor qu'unu.

Ecuación de la hipérbola na so forma complexa

Una hipérbola nel planu complexu ye'l llugar xeométricu formáu por un conxuntu de puntos ${\displaystyle z\,}$, nel planu ${\displaystyle ReIm\,}$; tales que, cualesquier d'ellos satisfai la condición xeométrica de que'l valor absolutu de la diferencia de les sos distancies ${\displaystyle |z-w_{1}|-|z-w_{2}|\,}$, a dos puntos fixos llamaos focos${\displaystyle w_{1}\,}$ y ${\displaystyle w_{2}\,}$, ye una constante positiva igual al doble de la distancia (esto ye ${\displaystyle 2l\,}$ ) qu'esiste ente'l so centru y cualesquier de los sos vértices de la exa focal.

La ecuación queda: ${\displaystyle |z-w_{1}|-|z-w_{2}|=2l\,}$

Evidentemente esta operación llevar a cabu nel conxuntu de los númberos complexos.

Ecuaciones en coordenaes polares

Dos hipérboles y los sos asíntotas en coordenaes cartesianes.

Hipérbola abierta de derecha a esquierda:

${\displaystyle r^{2}=a\sec 2\theta \,}$

Hipérbola abierta de riba abaxo:

${\displaystyle r^{2}=-a\sec 2\theta \,}$

Hipérbola abierta de nordés a suroeste:

${\displaystyle r^{2}=a\csc 2\theta \,}$

Hipérbola abierta de noroeste a sureste:

${\displaystyle r^{2}=-a\csc 2\theta \,}$

Hipérbola con orixe nel focu derechu:

${\displaystyle r(\theta )={\frac {a(\varepsilon ^{2}-1)}{1-\varepsilon \cos \theta }}}$

Hipérbola con orixe nel focu esquierdu:

${\displaystyle r(\theta )={\frac {a(\varepsilon ^{2}-1)}{1+\varepsilon \cos \theta }}}$

Ecuaciones paramétricas

Imaxe de seición cónica.

Hipérbola abierta de derecha a esquierda:

${\displaystyle {\begin{matrix}x=a\sec t+h\\y=b\tan t+k\\\end{matrix}}\qquad \mathrm {o} \qquad {\begin{matrix}x=\pm a\cosh t+h\\y=b\sinh t+k\\\end{matrix}}}$

Hipérbola abierta de riba abaxo:

${\displaystyle {\begin{matrix}x=a\tan t+h\\y=b\sec t+k\\\end{matrix}}\qquad \mathrm {o} \qquad {\begin{matrix}x=a\sinh t+h\\y=\pm b\cosh t+k\\\end{matrix}}}$

En toles fórmules (h,k) son les coordenaes del centru de la hipérbola, a ye'l llargor del semiexe mayor, b ye'l llargor del semiexe menor.

Elementos de la hipérbola

Exa mayor o real

La exa mayor ye la recta de la hipérbola onde pertenecen los focos y los vértices de la mesma. El so valor ye 2a y ye perpendicular a la exa imaxinaria

Exa menor o imaxinariu

La exa menor o imaxinariu nun tien puntos de mancomún cola hipérbola. Sicasí, siempres se cumple que les perpendiculares llanzaes pelos sos estremos corten coles perpendiculares llanzaes pelos estremos de la exa mayor en 4 puntos que pueden sirvir pa trazar les asíntotas.

Asíntotas

Son les rectes r y r' que pasen pel centru de la hipérbola y verifiquen que s'averen a les cañes al alloñar del centru de la hipérbola.

Les ecuaciones de les asíntotas son: r: y= b/a x r': y = -b/a r

Vértices

Los vértices d'una hipérbola son los puntos onde esta curtia a les sos exes.

Focos

Son dos puntos, ${\displaystyle F_{1}\,y\,F_{2}}$, respectu de los cualos permanez constante la diferencia de distancies (en valor absolutu) a cualquier puntu, ${\displaystyle x}$, de dicha hipérbola.

${\displaystyle \vert d(F_{1},x)-d(F_{2},x)\vert =cte}$

Centro

Puntu mediu de los vértices y de los focos de la hipérbola.

Tanxentes

La tanxente a una hipérbola en cualquier puntu de la curva ye bisectriz del ángulu formáu pelos radios vectores d'esi puntu.

Radiu de combadura

Sía'l puntu ${\displaystyle M(x_{0},y_{0})}$ de la hipérbola, entós el radiu de combadura ye

${\displaystyle R=a^{2}b^{2}({\frac {x_{0}^{2}}{a^{4}}}+{\frac {y_{0}^{2}}{b^{4}}})^{\frac {3}{2}}={\frac {(r_{1}\cdot r_{2})^{1.5}}{ab}}}$

, la ecuación de la hipérbola ye

${\displaystyle {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1}$

^[5]

Árees

01.Sía'l segmentu ${\displaystyle AMN}$ onde A, vértiz d'una caña; M y N estremos d'una cuerda perpendicular a la exa focal, entós l'área ye

${\displaystyle AMN=x\cdot y-a\cdot b\cdot \ln \left({\frac {x}{a}}+{\frac {y}{b}}\right)=a\cdot b\cdot \operatorname {Arch} {\frac {x}{a}}}$

02. Sía'l cuadriláteru curvu ${\displaystyle OAMG}$, onde O (orixe de coordenaes); segmentu OG sobre una asíntota; OA estremos centru y un vértiz; y ${\displaystyle M(xy)}$ un puntu de la hipérbola; MA un arcu d'hipérbola; L'área ye

${\displaystyle OAMG={\frac {a\cdot b}{4}}+{\frac {a\cdot b}{2}}\cdot \ln {\frac {2OG}{c}}}$^[6]

Ver tamién

• Xeometría analítica
• Seición cónica
• Recta
• Circunferencia
• Elipse
• Parábola
• Esferes de Dandelin