零知识证明

密码学中，零知識證明（英語：zero-knowledge proof）或零知識協議（zero-knowledge protocol）是一方（證明者）向另一方（檢驗者）證明某命題的方法，特點是過程中除「該命題為真」之事外，不泄露任何資訊。因此，可理解成「零洩密證明」。^[1]例如，欲向人證明自己擁有某情報，則直接公開該情報即可，但如此則會將該細節亦一併泄露；零知識證明的精粹在於，如何證明自己擁有該情報而不必透露情報內容。這也是零知識證明的難點。^[2]

若該命題的證明，需要知悉某秘密方能作出，則檢驗者單憑目睹證明，而未獲悉該秘密，仍無法向第三方證明該命題（即單單轉述不足以證明）。待證的命題中，必定包含證明者宣稱自己知道該秘密，但過程中不能傳達該秘密本身。否則，協議完結時，已給予檢驗者有關命題的額外的資訊。此類「知識的零知識證明」是零知識證明的特例，其中待證命題僅有「證明者知道某事」。

交互式零知識證明中，需要各方互動，靠通訊過程證明某方具備某知識，而另一方檢驗該證明是否成立。^[2]

也有某種非交互式零知識證明（英语：non-interactive zero-knowledge proof）^[3][4]，但證明之所以成立，依賴計算假設（典型假設是理想的密碼雜湊函數）。

生活範例

山洞中，小靜隨機選擇A路或B路，阿嚴則在洞外等候

阿嚴選一個出口

小靜準確出現在阿嚴所選的出口出現

以下有一個熟知的故事，總結零知識證明的若干重要概念。故事最早由Jean-Jacques Quisquater（英语：Jean-Jacques Quisquater）及同事發表於《如何向你的孩子解釋零知識協議》。^[5]設有小靜（證明者）和阿嚴（驗證者）兩人。^{[註 1]}

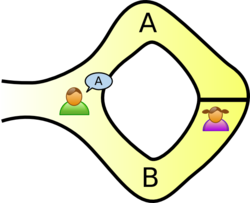
故事中，小靜發現洞穴中某扇魔法門的開門暗號。洞穴呈環形，入口在一側，對側則有魔法門隔斷。阿嚴想知小靜是否已知該暗號，但小靜很注重隱私，不希望泄露暗號予阿嚴，也不想全世界知道她有暗號之事。

兩人分別將入口左右兩條通道標示為A路、B路。首先，阿嚴在洞口外，待小靜進入洞內。小靜自行選擇行A路或B路，但阿嚴不准窺視小靜所選為何。然後，阿嚴行入洞穴，均勻隨機喊出A路或B路，表明希望小靜由該方向返回。假若小靜確實知道暗號，則很易達成，因為即使起初所選不是同一條路，她也可以開門通過，從另一條路返回。

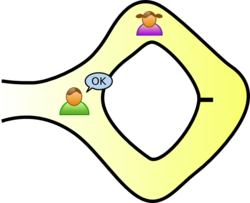
然而，若她其實不知道暗號，則祗有一半概率能從阿嚴所選的方向返回，因為阿嚴隨機選A路和B路，恰有一半機會選中起初小靜進入的方向。若兩人重複以上過程，比如連續20次，則小靜靠運氣全部碰巧從正確方向返回的概率极小，为2²⁰分之1。

所以，若小靜連續多次從阿嚴所選的方向返回，則阿嚴可以推斷，小靜很可能知道暗號。

以下考慮第三方的觀點。即使假設阿嚴佩戴隱蔽的鏡頭，錄影所見的整個過程，鏡頭所見亦只有阿嚴喊「A！」小靜從A路返回；或阿嚴喊「B！」小靜從B路返回。此種片段極易由兩人共謀偽造（祗需小靜與阿嚴事前商討多次驗證中阿嚴將選該串A、B的次序），從而對第三方而言，不具說服力，即阿嚴無法藉此向第三方證明小靜知道暗號。事實上，即使錄影換成現場在阿嚴身旁監視亦同，因為兩人可能一早已協調綵排好。

但是，若阿嚴在鏡頭前擲硬幣，然後按該硬幣喊A或B，則協議不再零知識。該段錄影可能足以說服第三方，兩人無法偽造，因為阿嚴難以準確擲出預定的AB次序。於是，雖然證明過程沒有泄露暗號予阿嚴，但是阿嚴可藉此說服世人，證明小靜知道暗號，與小靜起初的意欲完全相反。不過，數碼的密碼學中，「擲硬幣」以伪随机数生成器實作，類似於一枚結果已預定好的硬幣，但該結果（由其随机种子（英语：Random seed）決定）僅有硬幣主人知道。若阿嚴的硬幣實際是以此法運作，則協議又回復為零知識協議，因為兩人又有可能共同偽造「實驗」結果，所以使用偽隨機數生成器與擲真硬幣不同，前者不會向世人泄露小靜知道暗號。

還有另一種做法，小靜以獨一次實驗已可向阿嚴證明自己知道暗號，而不泄漏。方法是，兩人一同走入洞口，然後阿嚴目送小靜沿A路走，沒有原路折返，但從B路返回。如此，小靜必然已向阿嚴證明自己知道暗號，而沒有告知阿嚴暗號。不過此種證明亦非零知識：若第三方觀察到過程，或阿嚴有錄影，則該證明對第三方具說服力。換言之，小靜無法宣稱自己與阿嚴串通，所以無法向第三方說該證明無效。如此，小靜無法控制何人得知她擁有暗號之事。

定義

零知識證明要具備下列三種性質：

完備（complete）

若所要證之事為真，則誠實（意即依協議行事）的證明者能說服誠實驗證者。

健全（sound）

若命題為假，則作弊證明者僅得極小機會能說服誠實驗證者該事為真。

零知識（zero-knowledge）

若命題為真，則驗證者除此之外，過程中沒有得悉任何其他資訊。換言之，僅知命題為真（而不知祕密本身）已足以「想像」出一個交互的情境，其中證明者的確知道該秘密。此性質能嚴格定義為：每個驗證者皆有相應的模擬器，輸入欲證事實時，無需求助於證明者，已可輸出一套通訊謄本，看似誠實驗證者與證明者的通訊記錄。

前兩種性質，更廣義的交互式證明系統亦應具備。第三種性質使該交互證明稱為零知識。

零知識證明不算數學證明，因為尚允許有很少（但非零）概率，令作弊證明者能向驗證者「證明」假命題。該概率稱為可靠度誤差（soundness error）。換言之，零知識證明是概率「證明」，而非決定性。不過，也有技巧將可靠度誤差壓到忽略不計。

零知識的嚴格定義，需要抽象計算模型，如常見的图灵机。設${\displaystyle P}$、${\displaystyle V}$、${\displaystyle S}$為三部圖靈機。某語言${\displaystyle L}$的交互式证明系统^{[註 2]}${\displaystyle (P,V)}$為零知識，意思是對任意概率多項式時間（PPT）驗證者${\displaystyle {\widehat {V}}}$，皆有PPT模擬器${\displaystyle S}$使得：

${\displaystyle \forall x\in L,z\in \{0,1\}^{*},\operatorname {View} _{\widehat {V}}\left[P(x)\leftrightarrow {\widehat {V}}(x,z)\right]=S(x,z)}$

其中${\displaystyle \operatorname {View} _{\widehat {V}}\left[P(x)\leftrightarrow {\widehat {V}}(x,z)\right]}$是${\displaystyle P(x)}$與${\displaystyle {\widehat {V}}(x,z)}$間交互的全記錄。證明者${\displaystyle P}$通常假設具無限計算能力（實踐上，常為機率圖靈機）。直觀理解，某交互證明系${\displaystyle (P,V)}$為零知識，即對任意驗證者${\displaystyle {\widehat {V}}}$，皆存在某高效模擬器${\displaystyle S}$（視乎${\displaystyle {\widehat {V}}}$而定），給定任何輸入，可以重現${\displaystyle P}$與${\displaystyle {\widehat {V}}}$間的對話。定義中的輔助串${\displaystyle z}$，是用作放置任何「前備知識」（包括預知${\displaystyle {\widehat {V}}}$運行時擲得的硬幣結果）。定義推出，${\displaystyle {\widehat {V}}}$不能利用預知串${\displaystyle z}$從與${\displaystyle P}$的對話中發掘出資訊，因為若給予${\displaystyle S}$該串，則也同樣可以重現${\displaystyle {\widehat {V}}}$與${\displaystyle P}$間的對話。

以上為完美零知識的定義。若將定義中，驗證者${\displaystyle {\widehat {V}}}$的視角（view）與模擬相等之要求，改為僅要求計算上無法分辨（英语：computational indistinguishability），則得到計算零知識的定義。

計算範例

離散對數

前段概念適用於較實際的密碼學場景。設小靜欲向阿嚴證明，自己知道某群某指定元素的离散对数。^[6]

例如，給定數${\displaystyle y}$、质数${\displaystyle p}$、生成元${\displaystyle g}$，小靜希望證明自己知道某數${\displaystyle x}$使${\displaystyle g^{x}{\bmod {p}}=y}$，而不泄漏${\displaystyle x}$。事實上，知曉${\displaystyle x}$之事，本身可用作身份證明，即小靜可藉此證明該${\displaystyle y}$值是由她先暗中選某隨機值${\displaystyle x}$，再計算${\displaystyle y=g^{x}{\bmod {p}}}$，公諸所有潛在的驗證者。如此，若某人證明自己知道${\displaystyle x}$，則相當於證明自己即小靜，因為學者相信離散對數很難計算，即其他人無法從${\displaystyle y}$倒推出${\displaystyle x}$值。

證明協議如下：每輪，小靜預備隨機數${\displaystyle r}$，計算${\displaystyle C=g^{r}{\bmod {p}}}$，將該值傳予阿嚴。收到${\displaystyle C}$後，阿嚴隨機請求下列兩者之一：小靜公開${\displaystyle r}$值，或${\displaystyle (x+r){\bmod {(p-1)}}}$值。單獨看任何一個值，其分佈皆是均勻隨機，所以協議每輪皆不泄露任何機密。

阿嚴可以驗證所得回應。若問${\displaystyle r}$，則可以計算${\displaystyle g^{r}{\bmod {p}}}$，檢查是否等於${\displaystyle C}$。若問${\displaystyle (x+r){\bmod {(p-1)}}}$，則可以計算${\displaystyle g^{(x+r){\bmod {(p-1)}}}{\bmod {p}}}$，而該值應當等於${\displaystyle C\cdot y{\bmod {p}}}$，所以亦驗證${\displaystyle C}$值是否滿足該條件。若小靜確實知道${\displaystyle x}$值，理應很易回答阿嚴的任一條問題。

若小靜預知阿嚴採用何種盤問，則很易作弊，在不知${\displaystyle x}$的情況下，向阿嚴假裝自己知道${\displaystyle x}$：若她知道阿嚴將要問${\displaystyle r}$，則如常繼續，選${\displaystyle r}$，計算${\displaystyle C=g^{r}{\bmod {p}}}$，告知阿嚴${\displaystyle C}$值；她可以答出${\displaystyle r}$值。另一方面，若她知道阿嚴將問${\displaystyle (x+r){\bmod {(p-1)}}}$，則取隨機一個${\displaystyle r'}$值，計算${\displaystyle C'=g^{r'}\cdot \left(g^{x}\right)^{-1}{\bmod {p}}}$，然後發送${\displaystyle C'}$值予阿嚴（阿嚴會以為該值為${\displaystyle C}$值）。當阿嚴要求公開${\displaystyle (x+r){\bmod {(p-1)}}}$值時，小靜公開${\displaystyle r'}$，但這足以讓阿嚴驗證結果，因為他計算的值實為${\displaystyle g^{r'}{\bmod {p}}}$，是等於${\displaystyle C'\cdot y}$，因為${\displaystyle C'}$正是小靜一早乘上${\displaystyle y}$的逆元而計出。

然而，若有某輪驗證中，阿嚴的問題與小靜預估的有出入，則小靜無法計算出要答的結果（假定該群的離散對數問題難解）。若她揀選${\displaystyle r}$並公開${\displaystyle C=g^{r}{\bmod {p}}}$，則無法作弊給出服眾的${\displaystyle (x+r){\bmod {(p-1)}}}$值來通過阿嚴的檢查，因為不知道${\displaystyle x}$。又若她揀選${\displaystyle r'}$值，偽裝成${\displaystyle (x+r){\bmod {(p-1)}}}$，則要回答公開值的離散對數，但她無法回答，因為該值是由已知值乘出，而非某已知值以${\displaystyle g}$為底的冪，所以她不能計出其離散對數

所以，作弊的證明者僅得${\displaystyle 1/2}$概率通過某輪驗證。重複足夠多輪，成功作弊的概率可壓到任意小。

撮要

小靜要證知道${\displaystyle x}$值（如其密碼）。

1. 小靜與阿嚴約定某質數${\displaystyle p}$，及域${\displaystyle \mathbb {Z} /p\mathbb {Z} }$的乘法生成元${\displaystyle g}$。
2. 小靜計算${\displaystyle y=g^{x}{\bmod {p}}}$，傳送予阿嚴。
3. 重複以下步驟若干次：
   1. 小靜選某個均勻隨機數${\displaystyle r\in U[0,p-2]}$，計算${\displaystyle C=g^{r}{\bmod {p}}}$，傳送${\displaystyle C}$予阿嚴。
   2. 阿嚴問小靜${\displaystyle (x+r){\bmod {(p-1)}}}$或${\displaystyle r}$，二選其一。若問前者，則阿嚴驗證${\displaystyle (C\cdot y){\bmod {p}}\equiv g^{(x+r){\bmod {(p-1)}}}{\bmod {p}}}$。若問後者，則他驗證${\displaystyle C\equiv g^{r}{\bmod {p}}}$。

${\displaystyle (x+r){\bmod {(}}p-1)}$之值，可視為${\displaystyle x{\bmod {(}}p-1)}$的加密。若${\displaystyle r}$確為隨機，在${\displaystyle 0}$至${\displaystyle (p-2)}$間均勻分佈，則${\displaystyle (x+r){\bmod {(p-1)}}}$也同樣均勻分佈，所以不會泄漏任何關於${\displaystyle x}$的資訊（見一次性密碼本）。

大圖的哈密頓環

下列方案是曼紐爾·布盧姆提出。^[7]

此場境中，小靜知道某大圖${\displaystyle G}$的哈密頓環。阿嚴知道${\displaystyle G}$但不知該環（比如說小靜將該圖列印給阿嚴）。一般相信，找大圖的哈密頓環，在計算上並不可行，因為相應的決定問題已證為NP完全。小靜欲證自己知道該環，但不想泄漏出去，原因可能是阿嚴打算向小靜買，但付款前希望先驗證小靜知道；也可能是全世界衹得小靜知道該環，所以小靜向阿嚴證明此事，是為向阿嚴核實自己身份。

小靜為證明自己知道哈密頓環，與阿嚴作若干輪驗證。每輪中：

• 一開始，小靜預備圖${\displaystyle H}$，是與${\displaystyle G}$同構（即${\displaystyle H}$與${\displaystyle G}$一樣，但頂點的標籤不同）。若小靜知道${\displaystyle G}$的哈密頓環，則因為${\displaystyle H}$與${\displaystyle G}$間的同構由她揀選，她很易找到${\displaystyle H}$中對應的哈密頓環。
• 小靜秘諾${\displaystyle H}$。此處可選任意密碼學秘諾機制（英语：commitment scheme），甚或直接將${\displaystyle H}$的頂點編號，然後對${\displaystyle H}$的每條邊，將兩端編號寫在小紙片上，反轉蓋在枱面。總之，秘諾目的是使小靜此後無法竄改${\displaystyle H}$，但同時不讓阿嚴提早知道${\displaystyle H}$的資訊。
• 阿嚴隨機問小靜以下兩事之一：給出${\displaystyle H}$與${\displaystyle G}$間的同構（見圖同構問題（英语：graph isomorphism problem））；或給出${\displaystyle H}$的哈密頓環。
• 若問兩圖的同構，則小靜先展示${\displaystyle H}$（將枱面全部紙翻開），並給出${\displaystyle G}$頂點與${\displaystyle H}$頂點的對應表。阿嚴可以驗證該對應關係是否滿足圖同構的條件。
• 若問哈密頓環，則小靜衹翻開在${\displaystyle H}$的哈密頓環上的紙片。如此，阿嚴已可驗證${\displaystyle H}$有哈頓頓環。

秘諾一步必須使阿嚴在第二種情況能驗證該環確實由${\displaystyle H}$的邊構成。一種做法是，逐條邊分別秘諾。

完備

若小靜確知${\displaystyle G}$中的哈密頓環，則阿嚴詢問同構時，她很易回答（該同構為她所選），而阿嚴問${\displaystyle H}$中的哈密頓環時，她同樣很易回答（${\displaystyle G}$有哈密頓環，${\displaystyle G}$與${\displaystyle H}$間的同構為所她選，所以可以找到${\displaystyle H}$中對應的環）。

健全

若小靜不知哈密頓環，則衹能預先猜測阿嚴會問何種問題，相應準備某個與${\displaystyle G}$同構的圖，或另一個不相關的哈密頓圖。然而，因為她不知${\displaystyle G}$的哈密頓環，所以無法同時做兩件事。於是，若以上驗證重複${\displaystyle n}$次，則小靜蒙混過關的概率僅得${\displaystyle 2^{-n}}$，從而實際意義上，衹需合理多輪驗證，已使造假者寸步難行。

零知識

小靜的回答不泄漏原圖${\displaystyle G}$的哈密頓環，因為每一輪，阿嚴衹會得悉${\displaystyle H}$與${\displaystyle G}$的同構，或是${\displaystyle H}$的哈密頓環，兩者之一，但他需要對同一個${\displaystyle H}$同時得知兩者，纔能構造出${\displaystyle G}$中的哈密頓環。如此，衹要小靜每輪預備一幅不同的圖${\displaystyle H}$，就能保密。若小靜不知${\displaystyle G}$的哈密頓環，但不知為何已事前得知阿嚴每輪會問的問題，則她可以作弊。例如，若小靜預知阿嚴該輪會問${\displaystyle H}$的哈密頓圖，則大可以祕諾一幅與${\displaystyle G}$無關的哈密頓圖。與之類似，若小靜預知阿嚴會問同構表，則她可以隨便預備一幅與${\displaystyle G}$同構的圖${\displaystyle H}$（其中她不知道任何哈密頓圖）。阿嚴根本無需小靜在場，亦可獨自想像出自己將見的場面，因為他清楚自己將會問甚麼，將見的僅是一個環（而不顯示圖的其他部分）或一幅與${\displaystyle G}$同構的圖，即阿嚴可以自行模擬該協議。因此，阿嚴從每一輪驗證揭露之事，無法得到任何關於${\displaystyle G}$哈密頓環的資訊。

零知識條件的變式

「零知識」的定義有若干變形，分別在於如何嚴謹定義模擬結果「看似」真實的交互記錄：

完美零知識（perfect zero-knowledge）

模擬器與真正交互產生的概率分佈完全相等。離散對數範例即屬此類。

統計零知識（statistical zero-knowledge）

兩個分佈並非完全相等，但統計上接近（英语：statistically close），即有某個可忽略函數，使該兩列分佈^{[註 3]}在任意集合取值的概率差，皆小於該函數。^[8]

計算零知識（computational zero-knowledge）

無高效算法分辨兩個分佈。

應用

身份驗證

零知識證明的研究，是受身份驗證系統啟發。驗證時，一方要向另一方證明自己身份，通常藉賴證明自己持有某種袐密（如通行密碼），但不希望對方知悉該袐密，稱為零知識知識證明（英语：proof of knowledge）。不過，通行密碼一般不是太短，就是不夠隨機，不能用於許多零知識知識證明方案。零知識通行碼證明（英语：zero-knowledge password proof）就是有考量密碼長度限制的一類零知識知識證明。^{[來源請求]}

2015年4月，Sigma協議（「其中之一」證明，英語：one-out-of-many proofs）面世。^[9]2021年8月，美國網絡基建、安全公司Cloudflare採用該種證明機制，以供應方硬件^{[請求校對翻譯]}為私人網絡提供驗證服務。^[10]

道德行為

密碼學協議之中使用零知識證明，可以在不退讓隱私的情況下，確保各方誠實。粗略言之，方法是迫用戶零知識地證明，其所作所為是依足協議。^[11][12]由健全性，用戶必先確實跟從協議，纔能服眾。又由於證明是零知識，此過程並無犠牲用戶的隱私。

核裁軍

2016年，普林斯頓電漿物理實際室與普林斯頓大學展示一個技巧，或許適用於未來的核裁軍談判。其特點是，無需揭露某物件內部的機密構造，亦可允許督查員判斷該物件是否核武器。^[13]

區塊鏈

零知識證明用於小零幣（英语：Zerocoin protocol）與大零幣協議中，最終於2016年發展成小零幣（英语：Zcoin）^[14]（2020年改稱飛熔幣（英语：Firo (cryptocurrency)））^[15]和大零幣兩種加密貨幣。小零幣內置有混幣模型，以確保匿名，且該模型無需信任任何對等用戶或中央集權混幣者。^[14]用戶可以用另一種基準幣交易，也可以將該幣賣出買入小零幣。^[16]:118大零幣協議的模型也類似（該變式稱為非交互式零知識證明（英语：Non-interactive zero-knowledge proof））^[17]，而且可以掩蓋交易額，但小零幣則不能。大零幣的交易數據如此隱密，所以與小零幣相比，較不易受到隱私計時攻擊（英语：Timing attack）。不過，此層額外隱私，可能導致不能追蹤假幣，倘因此造成大零幣供給的超通漲，可能無法偵測到。^[14][18]

2018年，防彈證明（bulletproofs）面世。其改進自非交互式零知識證明，不再需要可信的安裝環境。^[19]其後，實作成「結舌」協議（Mimblewimble protocol，Grin和Beam兩種加密幣皆出自該協議）和门罗币。^[20]2019年，飛熔幣實作Sigma協議（英语：Proof of knowledge），是對應小零幣協議無可信環境的改進。^[21][9]同年，飛熔幣引入萊蘭托斯協議（Lelantus protocol），更自Sigma協議改進，隱去交易的源頭與金額。^[22]

沿革

零知識證明最早由莎菲·戈德瓦塞尔、希爾維奧·米卡利、查爾斯·拉克福（英语：Charles Rackoff）三人於1985年發表，論文題為《交互式證明系統的知識複雜度》。^[11]該論文引入交互式证明系统的IP複雜度類（英语：IP (complexity)），並構想出「知識複雜度」概念，衡量證明過程中，由證明者傳遞予驗證者的知識量。三人亦給出首個具體問題的零知識證明，即零知識地證明某數不是模 m 的二次剩余。連同鲍鲍伊·拉茲洛（英语：László Babai）與什洛莫·莫蘭（英语：Shlomo Moran）的另一篇論文，戈-米-拉三氏的論文發明了交互式證明系統。為此，五人同獲1993年首屆哥德尔奖。

引述戈-米-拉三氏：

該額外知識基本為0的情況尤其值得關注。我等證明，可以交互地證明某數非模 m 的二次剩餘，而釋出零額外知識。其出奇之處是，若不給定 m 的分解，則無高效算法判別某數是否模 m 的二次剩餘。更甚者，任何已知的NP證明皆要表明 m 的質因數分解。這就表明，在證明過程中添加互動，可能減少證明某定理所必須交流的知識。 ^{[註 4]}

二次非剩餘問題既有NP算法又有反NP算法，故位處NP與反NP兩類之交集中。其後找到有零知識證明的若干個問題，亦具同樣的性質，例如歐迪·戈德賴希（英语：Oded Goldreich）未經正式出版的證明系統，可以驗證某數（為兩個未知質數之積）不是布盧姆整數，即並非兩個模4餘3的質數之積。^[23]

歐迪·戈德賴希（英语：Oded Goldreich）、希爾維奧·米卡利、阿维·威格森更進一步證明，假定存在無懈可擊的加密法，則可以造出三色圖着色問題的零知識證明系統，而該問題本身為NP完全。又因為每個NP問題都可以高效化歸成該NP完全問題，所以在前述假定下，所有NP問題皆有零知識證明。^[24]需要該假定的原因是，正如前節範例，需要有秘諾的手段。若存在單向函數，則的確有牢不可破的加密法。此為廣泛引用的充分條件。另外也可能有物理方法實作。

更上一層樓，他們亦證明，圖不同構問題（英语：graph nonisomorphism problem），即圖同構問題（英语：graph isomorphism problem）之補（英语：complement (complexity)），有零知識證明。該問題已知屬於反NP，但未知是否屬於NP或其他實際可行的複雜度類。更一般地，羅素·英帕利亞佐（英语：Russell Impagliazzo）、莫迪凱·容（英语：Moti Yung）^{[譯名請求]}二人，與米高·本-奧爾（Michael Ben-Or）及同事，兩組證明：同樣假設存在單向函數或牢不可破的加密，則任何屬於IP（已證等於PSPACE）的問題，皆有零知識證明。換言之，任何命題若可藉交互系統證明，則可零知識證明。^[25][26]

許多理論家不希望假設不必要的條件，所以試圖在不假定單向函數的條件之下，證明同樣的結論。有種做法稱為「多證明者交互式證明系統」（見交互式证明系统），即有多個獨立的證明者，而非僅得一個。驗證者可以將證明者逐個孤立，然後詰問，以免被作弊證明者誤導。無需任何難解假設，已可證明在此系統中，任何NP問題皆有零知識證明。^[27]

後來發現，互聯網等同時執行多個協議的環境中，較難構造零知識證明。研究並行零知識證明的先驅是辛西婭·德沃克（英语：Cynthia Dwork）、莫尼·納奧爾（英语：Moni Naor）、阿米特·薩海（英语：Amit Sahai）。^[28]此類研究之中，重要成果有證據不可辨（英语：witness-indistinguishable proof）協議。與零知識相比，其性質較弱：可能有多種證據供證明者選擇採用何者作證，此時僅要求驗證者無法分辨證明者選擇為何^{[註 5]}，但證明者可以泄漏部分資訊，如全體證據組成的集合。儘管失去零知識性質，但此類協議的好處是，並行時不會遇到此前提及的問題。^[29]

變式尚有非交互式零知識證明（英语：non-interactive zero-knowledge proof）。曼纽尔·布卢姆、保羅·費爾德曼（Paul Feldman）、米卡利證明，若證明者與驗證者共有一條隨機字串，則可以達成計算零知識，而毋須交互。^[3][4]

參見

• 配對式密碼學（英语：Pairing-based cryptography）：給定${\displaystyle f(x)}$與${\displaystyle f(y)}$，無需知道${\displaystyle x}$、${\displaystyle y}$，已可計算${\displaystyle f(x\times y)}$。
• 安全多方计算：各方的輸入值保密，但共同計算出該些輸入對應的結果。
• 圈子簽名（英语：Ring signature）：可以簽署某文件，使圈外人無法得悉由圈內何人署名，衹知圈內有某人署名。
• 阿羅資訊悖論（英语：Arrow information paradox）
• 密碼學協議
• 費蓋-菲亞特-薩莫爾身份認證（英语：Feige–Fiat–Shamir identification scheme）
• 密碼學諸主題

註

1. 英文文獻中，常稱零知識協議中的證明者為Peggy（取prover的首字母）、驗證者Victor（verifier的首字母），見愛麗絲與鮑伯。
2. 即欲證事實為某字串${\displaystyle x\in L}$。
3. 對不同輸入規模（安全參數），各有模擬器與真正交互此兩個分佈。
4. 原文作 "Of particular interest is the case where this additional knowledge is essentially 0 and we show that [it] is possible to interactively prove that a number is quadratic non residue mod m releasing 0 additional knowledge. This is surprising as no efficient algorithm for deciding quadratic residuosity mod m is known when m’s factorization is not given. Moreover, all known NP proofs for this problem exhibit the prime factorization of m. This indicates that adding interaction to the proving process, may decrease the amount of knowledge that must be communicated in order to prove a theorem."
5. 即無法分辨該證明者與採用另一證據的證明者。

參考文獻

1. 林之晨. 區塊鏈的「零知識證明」是什麼東西？. 天下雜誌. 2018-11-05, 660.
2. What is a zero-knowledge proof and why is it useful?. 16 November 2017 [2021-11-17]. （原始内容存档于2019-06-07）.
3. Blum, Manuel; Feldman, Paul; Micali, Silvio. Non-Interactive Zero-Knowledge and Its Applications. 1988: 103–112. ISBN 978-0897912648. S2CID 7282320. doi:10.1145/62212.62222. |journal=被忽略 (帮助)^{[失效連結]}
4. Wu, Huixin; Wang, Feng. A Survey of Noninteractive Zero Knowledge Proof System and Its Applications. The Scientific World Journal. 2014, 2014: 560484. PMC 4032740 . PMID 24883407. doi:10.1155/2014/560484.
5. Quisquater, Jean-Jacques; Guillou, Louis C.; Berson, Thomas A. How to Explain Zero-Knowledge Protocols to Your Children (PDF). Lecture Notes in Computer Science 435. 1990: 628–631. ISBN 978-0-387-97317-3. doi:10.1007/0-387-34805-0_60. |journal=被忽略 (帮助)
6. Chaum, David; Evertse, Jan-Hendrik; van de Graaf, Jeroen. An Improved Protocol for Demonstrating Possession of Discrete Logarithms and Some Generalizations. Lecture Notes in Computer Science 304. 1987: 127–141. ISBN 978-3-540-19102-5. doi:10.1007/3-540-39118-5_13. |journal=被忽略 (帮助)
7. Blum, Manuel. How to Prove a Theorem So No One Else Can Claim It. ICM Proceedings. 1986: 1444–1451. CiteSeerX 10.1.1.469.9048 .
8. Sahai, Amit; Vadhan, Salil. A complete problem for statistical zero knowledge (PDF). Journal of the ACM. 1 March 2003, 50 (2): 196–249. CiteSeerX 10.1.1.4.3957 . S2CID 218593855. doi:10.1145/636865.636868. （原始内容存档 (PDF)于2015-06-25）.
9. Groth, J; Kohlweiss, M. One-Out-of-Many Proofs: Or How to Leak a Secret and Spend a Coin. Annual International Conference on the Theory and Applications of Cryptographic Techniques. Lecture Notes in Computer Science (Berlin, Heidelberg: EUROCRYPT 2015). 14 April 2015, 9057: 253–280. ISBN 978-3-662-46802-9. doi:10.1007/978-3-662-46803-6_9.
10. Introducing Zero-Knowledge Proofs for Private Web attestation with Cross/Multi-Vendor Hardware. The Cloudflare Blog. 2021-08-12 [2021-08-18]. （原始内容存档于2021-12-13） （英语）.
11. Goldwasser, S.; Micali, S.; Rackoff, C., The knowledge complexity of interactive proof systems (PDF), SIAM Journal on Computing, 1989, 18 (1): 186–208 [2021-11-21], ISSN 1095-7111, doi:10.1137/0218012, （原始内容存档 (PDF)于2021-10-21）
12. Abascal, Jackson; Faghihi Sereshgi, Mohammad Hossein; Hazay, Carmit; Ishai, Yuval; Venkitasubramaniam, Muthuramakrishnan. Is the Classical GMW Paradigm Practical? The Case of Non-Interactive Actively Secure 2PC. Proceedings of the 2020 ACM SIGSAC Conference on Computer and Communications Security. CCS '20 (Virtual Event, USA: Association for Computing Machinery). 2020-10-30: 1591–1605. ISBN 978-1-4503-7089-9. doi:10.1145/3372297.3423366.
13. PPPL and Princeton demonstrate novel technique that may have applicability to future nuclear disarmament talks - Princeton Plasma Physics Lab. www.pppl.gov. [2022-03-22]. （原始内容存档于2021-09-21）.
14. Hellwig, Daniel; Karlic, Goran; Huchzermeier, Arnd. Privacy and Anonymity. Build your own blockchain - A practical guide to distributed ledger technology. SpringerLink. 3 May 2020: 112 [3 December 2020]. ISBN 9783030401429. doi:10.1007/978-3-030-40142-9_5. （原始内容存档于2021-11-21）.
15. Hurst, Samantha. Zcoin Announces Rebranding to New Name & Ticker "Firo". Crowdfund Insider. [4 November 2020]. （原始内容存档于30 October 2020）.
16. Bonneau, J; Miller, A; Clark, J; Narayanan, A. SoK: Research Perspectives and Challenges for Bitcoin and Cryptocurrencies. 2015 IEEE Symposium on Security and Privacy (San Jose, Carlifornia). 2015: 104–121 [2021-11-21]. （原始内容存档于2022-02-10）.
17. Ben-Sasson, Eli; Chiesa, Alessandro; Garman, Christina; Green, Matthew; Miers, Ian; Tromer, Eran; Virza, Madars. Zerocash: Decentralized Anonymous Payments from Bitcoin (PDF). IEEE. 18 May 2014 [26 January 2016]. （原始内容存档 (PDF)于2022-02-08）.
18. Orcutt, Mike. A mind-bending cryptographic trick promises to take blockchains mainstream. MIT Technology Review. [2017-12-18]. （原始内容存档于2019-08-15） （英语）.
19. Bünz, B; Bootle, D; Boneh, A. Bulletproofs: Short Proofs for Confidential Transactions and More. IEEE Symposium on Security and Privacy (San Francisco, Carlifornia). 2018: 315–334 [3 December 2020]. ISBN 978-1-5386-4353-2. S2CID 3337741. doi:10.1109/SP.2018.00020 . （原始内容存档于2022-01-21）.
20. Odendaal, Hansie; Sharrock, Cayle; Heerden, SW. Bulletproofs and Mimblewimble. Tari Labs University. [3 December 2020]. （原始内容存档于29 September 2020）.
21. Andrew, Munro. Zcoin cryptocurrency introduces zero knowledge proofs with no trusted set-up. Finder Australia. 30 July 2019 [30 July 2019]. （原始内容存档于30 July 2019）.
22. Aram, Jivanyan. Lelantus: Towards Confidentiality and Anonymity of Blockchain Transactions from Standard Assumptions. Cryptology ePrint Archive. 7 April 2019, (Report 373) [14 April 2019]. （原始内容存档于2019-04-14）.
23. Goldreich, Oded. A zero-knowledge proof that a two-prime moduli is not a Blum integer. Unpublished Manuscript. 1985.
24. Goldreich, Oded; Micali, Silvio; Wigderson, Avi. Proofs that yield nothing but their validity. Journal of the ACM. 1991, 38 (3): 690–728. CiteSeerX 10.1.1.420.1478 . S2CID 2389804. doi:10.1145/116825.116852.
25. Russell Impagliazzo, Moti Yung: Direct Minimum-Knowledge Computations. CRYPTO 1987: 40-51
26. Ben-Or, Michael; Goldreich, Oded; Goldwasser, Shafi; Hastad, Johan; Kilian, Joe; Micali, Silvio; Rogaway, Phillip. Everything provable is provable in zero-knowledge. Goldwasser, S. (编). Advances in Cryptology—CRYPTO '88. Lecture Notes in Computer Science 403. Springer-Verlag. 1990: 37–56.
27. Ben-or, M.; Goldwasser, Shafi; Kilian, J.; Wigderson, A. Multi prover interactive proofs: How to remove intractability assumptions (PDF). Proceedings of the 20th ACM Symposium on Theory of Computing. 1988: 113–121 [2021-11-27]. （原始内容存档 (PDF)于2007-04-17）.
28. Dwork, Cynthia; Naor, Moni; Sahai, Amit. Concurrent Zero Knowledge. Journal of the ACM. 2004, 51 (6): 851–898. CiteSeerX 10.1.1.43.716 . S2CID 52827731. doi:10.1145/1039488.1039489.
29. Feige, Uriel; Shamir, Adi. Witness Indistinguishable and Witness Hiding Protocols. 1990: 416–426. CiteSeerX 10.1.1.73.3911 . ISBN 978-0897913614. S2CID 11146395. doi:10.1145/100216.100272. |journal=被忽略 (帮助)