数学物理
来自维基百科,自由的百科全书
数学物理是数学和物理学的交叉领域,指应用特定的数学方法来研究物理学的某些部分。对应的数学方法也叫数学物理方法。数学和物理学的发展在历史上一直密不可分,许多数学理论是在物理问题的基础上发展起来的;很多数学方法和工具通常也只在物理学中找到实际应用。不過,也只是互相參考而已,沒有所謂的一定。[1]

范围
数学物理有多个分支,大致对应特定历史时期。
将数学物理技术应用于经典力学,通常涉及用拉格朗日力学和哈密顿力学(包括有约束时的两种方法)对牛顿力学进行严格抽象的重新表述。这两种表述都体现在分析力学中,使人们理解动力系统动态演化过程中对称性与守恒定律间的深刻相互作用,体系拿在诺特定理的最基本表述中。这些方法与思想已经推广到物理学的其他领域,如统计力学、连续介质力学、经典场论、量子场论等。此外,它们还为微分几何提供了很多例子与见解(如辛几何与向量丛中的多个概念)。
数学中,偏微分方程、变分法、傅里叶分析、位势论、向量分析等也许与数学物理的联系最密切。18世纪下半叶(如让·勒朗·达朗贝尔、莱昂哈德·欧拉、约瑟夫·拉格朗日)到1930年代,这些领域得到了蓬勃发展。发展的物理应用如流体力学、天体力学、连续介质力学、弹性理论、声学、热力学、电学、磁学与空气动力学。
原子光谱理论(及后来的量子力学)几乎与线性代数、算子谱理论、算子代数、更广泛的泛函分析等领域的某些部分同时发展。非相对论量子力学包括薛定谔算,与原子分子物理学有关。量子信息论是另一个分支学科。
狭义相对论和广义相对论需要相当不同类型的数学,这就是群论,在量子场论和微分几何中发挥重要作用。宇宙学和量子场论现象的数学描述中,拓扑学和泛函分析逐渐对其进行了补充。同调代数和范畴论的一些概念也很重要。[2]
统计力学是独立领域,包括相变理论,依赖于哈密顿力学(或其量子版本),并与更数学的遍历理论及概率论的某些部分密切相关。组合学与物理学,特别是统计物理学之间的互动日益频繁。
用途
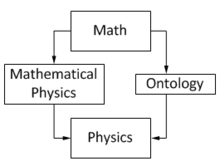
“数学物理”一词的用法有时很特殊。最早来自物理学的一些数学部分并不被视作数学物理的一部分,例如常微分方程和辛几何通常归为纯数学学科,动力系统与哈密顿力学之类则归入数学物理。
“数学物理”有时用来指在数学严谨框架内研究物理问题与思想实验的研究,这样,数学物理涵盖了非常广的学术领域。虽然数学物理与理论物理学有关,[3]这个意义上,数学物理强调类似于数学的物理严谨性。
另一方面,理论物理强调与观测和实验物理学的联系,往往要求理论物理学家(及更一般意义的数学物理学家)使用启发式、直觉或近似的论证。[4]而数学家并不认为这种论证是严谨的。
这种数学物理学家关注物理理论的推广与阐述。由于对数学严谨性的要求,他们常常要处理理论物理学家认为已解决的问题,不过也能指出现有解决方法的不完善。例子如从统计力学推断热力学第二定律,狭义与广义相对论中同步过程的微妙处(萨格纳克效应与爱因斯坦同步法)。
将物理理论建立于严格数学基础上的努力不仅发展了物理学,也影响了很多数学领域,例如量子力学的发展与泛函分析的很多方面并行不悖。量子力学、量子场论和量子统计力学的数学研究推动了算子代数的成果,对量子场论进行严格数学表述的尝试也在表示论等领域取得进展。
著名数学物理学家
对自然现象进行数学分析的传统可追溯到古希腊时代,如欧几里得《光学》、阿基米德《平面图形的平衡或其重心》《论浮体》、托勒密《光学》《谐和论》等。[5][6]后来伊斯兰、拜占庭学者们在这些著作基础上加以发展,L最终在12世纪和文艺复兴重新引入了欧洲。
16世纪前十年,业余天文学家尼古拉斯·哥白尼提出了日心说,并在1543年发表了相关论文,保留了托勒密的本轮,只构建更简单的本轮轨道以简化天文学。本轮包含很多个圆,而根据亚里士多德物理学,圆是运动的完美形式,是亚里士多德第五元素(以太)的内在运动,也是天体的纯净成分。第谷·布拉厄的助手约翰内斯·开普勒(1571–1630)将哥白尼轨道修正为椭圆,形式化为开普勒定律。
伽利略·伽利雷是狂热的原子论者,在《试金者》(The Assayer,1623)中断言“自然之书是用数学写成的”。[7]他在1632年出版的关于望远观测的书中支持日心说。[8]引入实验后,伽利略又通过反驳亚里士多德物理学本身来驳斥地心宇宙学。《关于两门新科学的论述》(1638)中确立了等距自由落体定律和惯性运动原理,为今日的经典力学奠定了核心概念。[8]根据伽利略惯性定律和伽利略不变性原理(也称伽利略相对论),对任何有惯性的物体,只能从经验知道是处于相对静止还是相对运动(相对于另一物体)。
勒内·笛卡尔以涡旋运动原理为基础,发展出一套完整的日心宇宙学体系,这就是笛卡尔物理学,导致了亚里士多德物理学的消亡。笛卡尔试图将科学中的数学推理形式化,发展了笛卡尔坐标系以在三维空间中几何地绘制位置图,并在时间流中标记位置变化。[9]
与牛顿同时代的克里斯蒂安·惠更斯是第一个通过一组参数将物理问题理想化的人,也是第一个将不可观测物理现象的力学解释完全数学化的人。因此,惠更斯被认为是第一位理论物理学家和现代数学物理的奠基人。[10][11]
微积分的重要概念(如微积分基本定理,1668年由苏格兰数学家詹姆斯·格雷果里证明[12]、用费马定理由微分求函数极值)在牛顿和莱布尼茨之前就已为人所知。艾萨克·牛顿(1642–1727)提出了微积分的一些概念(戈特弗里德·莱布尼茨在物理学之外也提出了类似概念),和解决物理问题用的牛顿法。将微积分应用于运动理论的尝试取得了巨大成功,载于《自然哲学的数学原理》(1687)[13],其中将三个伽利略运动定律和牛顿万有引力定律建立在绝对空间的框架上——牛顿将其假定为欧氏结构向所有方向无限延伸的物理实体;还假定了绝对时间,假定绝对运动(物体相对于绝对空间的运动)合理。伽利略不变性/相对性隐含在牛顿运动理论中。表面上看,牛顿将开普勒的天体运动和伽利略的地面运动归结为一种统一的运动,从而实现了数学严谨,而在理论上显得松懈。[14] 18世纪,瑞士丹尼尔·伯努利(1700–1782)在流体力学和弦振动方面做出了贡献。瑞士莱昂哈德·欧拉(1707–1783)在变分法、动力学、流体力学等领域做出了突出贡献。法国籍意大利裔约瑟夫·拉格朗日(1736–1813)在分析力学(提出拉格朗日力学)和变分法方面的工作也很突出。爱尔兰物理学家、天文学家与数学家威廉·哈密顿(1805-1865)提出了哈密顿力学,在现代物理理论(包括场论与量子力学)的形成中发挥了重要作用。法国数学物理学家约瑟夫·傅里叶(1768 – 1830)引入了傅立叶级数求解热传导方程式,从而产生了一种用积分变换求解偏微分方程的新方法。
到19世纪初,法国、德国与英国数学家相继对数学物理做出贡献。法国皮埃尔-西蒙·拉普拉斯(1749–1827)在数学天文学、位势论方面做出了重大贡献。西梅翁·德尼·泊松(1781–1840)致力于分析力学和位势论。在德国,卡尔·弗里德里希·高斯(1777–1855)对电学、磁学、力学和流体力学做出重要贡献。在英国,乔治·格林(1793-1841)的《数学分析在电磁理论中的应用》(1828)除了对数学的重大贡献,还在电学与磁学的数学基础上取得了早期进展。
在牛顿发表光的粒子论前几十年,荷兰克里斯蒂安·惠更斯(1629–1695)提出了光的波动论(1690)。1804年,托马斯·杨的双缝实验发现光的衍射,成为波动说的重要论据,惠更斯的以太说得到接受。奥古斯丁·菲涅耳对以太的假设行为进行了建模。英国物理学家迈克尔·法拉第引入了场的理论概念(而非远距离作用)。19世纪中叶,苏格兰詹姆斯·克拉克·麦克斯韦(1831–1879)将电学和磁学归结为麦克斯韦电磁场理论,后来精简为麦克斯韦方程组。最初,人们发现光学是麦克斯韦场的结果,后来发现辐射与今日所谓电磁波谱也是这个电磁场的结果。
英国物理学家约翰·斯特拉斯(1842–1919)研究了声音。爱尔兰威廉·哈密顿(1805–1865)、乔治·斯托克斯(1819–1903)与开尔文勋爵(1824–1907)完成了多部重要著作:斯托克斯是光学和流体力学的领军人物;开尔文在热力学方面做出了重大发现;哈密顿在分析力学领域做出突出贡献,开发出了哈密顿力学。他的德国同事数学家卡尔·雅可比(1804–1851)对这方法做出了非常重要的共线,特别是在正则变换方面。德国赫尔曼·冯·亥姆霍兹(1821–1894)在电磁学、波、流体、声学领域做出重大贡献。在美国,乔赛亚·威拉德·吉布斯(1839–1903)的开创性工作成为统计力学的基础。德国路德维希·玻尔兹曼(1844-1906)取得了这领域的基础理论成果,共同奠定了电磁理论、流体力学与统计力学的基础。
到1880年代,出现了一个突出的悖论:麦克斯韦电磁场中的观察者以近似恒定速度测量电磁场,而与观察者相对于场中其他物体的速度无关。因此,虽然相对于电磁场,观察者的速度会不断丢失,但相对于电磁场中的其他物体,观察者的速度却保持不变。然而,在物体间的相互作用中,并没有违反伽利略不变性的现象。由于麦克斯韦电磁场被模拟为以太的振动,时人推断,在以太内运动会产生以太漂移,扭曲电磁场,这就解释了观察者速度的流失。伽利略变换是将参照系中位置转换为另一参照系位置的数学过程,都发生于笛卡尔坐标系中;这过程被洛伦兹变换取代,得名于荷兰亨德里克·洛伦兹(1853–1928)。
1887年,实验家Michelson和Morley没能探测到以太漂移。有人假设,进入以太的运动也会使以太缩短,如洛伦兹变换所模拟。据此假设,以太使电磁场在所有惯性系中都符合伽利略不变性,而牛顿运动定律则幸免。
奥地利物理学家、哲学家恩斯特·马赫批评了牛顿假设的绝对空间。数学家亨利·庞加莱(1854–1912)甚至对绝对时间也提出质疑。1905年,皮埃尔·迪昂发表了对牛顿运动理论基础的毁灭性批判。[14]同年,阿尔伯特·爱因斯坦(1879–1955)发表了狭义相对论,通过摒弃以太,对电磁场不变性与伽利略不变性做出了新阐述。与牛顿的绝对时空相对,狭义相对论考虑的是相对时空,物体在运动过程中长度收缩、时间膨胀。
1908年,爱因斯坦的前数学教授赫尔曼·闵可夫斯基将三维空间与一维时间模型化,将时间轴视作第四个空间维度。[15]爱因斯坦最初称其为“多余的学问”,但后来在广义相对论中非常优雅地使用了闵可夫斯基时空,[16]将不变性推广到所有参考系,并将此归功于当时已去世的闵可夫斯基。广义相对论用广义坐标取代了笛卡尔坐标,用引力场取代了牛顿假设的欧氏空间假想引力(即时超距作用)。引力场就是闵可夫斯基时空本身,即爱因斯坦以太的4维拓扑,以洛伦兹流形为模型,根据黎曼曲率张量几何地弯曲。牛顿引力的概念:“两质量相互吸引”代以几何论证:在质能附近,“质量改变了时空曲率,有质量的自由粒子沿时空间的测地线运动”。(1850年代,高斯和伯恩哈德·黎曼为寻找内蕴几何与非欧几何,已经提出了黎曼几何。)狭义相对论下,即便是无质能量也会通过质能等价局部扭曲4维时空,产生引力效应。
20世纪另一革命性进展是量子理论,源于马克斯·普朗克(1856–1947)关于黑体辐射的开创性贡献与爱因斯坦对光电效应的研究。1912年,数学家亨利·庞加莱发表了《量子理论研究》(Sur la théorie des quanta)。[17][18]他在这篇论文中首次提出了量子化的形式定义。早期量子物理的发展遵循阿诺尔德·索末菲(1868–1951)和尼尔斯·玻尔(1885–1962)设计的启发式框架,很快被马克斯·玻恩(1882–1970)、维尔纳·海森堡(1901–1976)、保罗·狄拉克(1902–1984)、埃尔温·薛定谔(1887–1961)、萨特延德拉·纳特·玻色(1894–1974)、沃尔夫冈·泡利(1900–1958)发展的量子力学所取代。这一革命性理论框架基于对状态、演化与测量的概率解释,即无限维向量空间上的自伴算子。这空间称作希尔伯特空间(数学家大卫·希尔伯特(1862–1943)、埃哈德·施密特(1876–1959)、里斯·弗里杰什(1880–1956)为寻求欧氏空间的推广与研究积分方程而引入)。约翰·冯·诺依曼在《量子力学的数学基础》中严格定义了公理化的现代版本,并建立了希尔伯特空间现代泛函分析的相关部分——谱理论(大卫·希尔伯特引入,研究了无穷多变量的二次型。多年后,人们发现谱理论与氢原子光谱有关,他对这应用非常惊讶)。保罗·狄拉克用代数构造为电子建立了相对论模型,预言了电子的磁矩及其反粒子——正电子的存在。
主要内容
另见
脚注
参考文献
阅读更多
外部链接
Wikiwand - on
Seamless Wikipedia browsing. On steroids.
