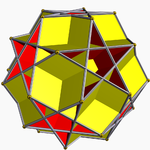
大十二面半二十面體是一種擬正半多面體[1],由12個五邊形面和10個穿過整體幾何中心的六邊形面組成,[2]外觀看起來像每個五角星都向內凹陷的截半大十二面體[3]:158。由於其每個面都是正多邊形,且每個頂點對應的角皆相等,因此也可以被歸類為擬正多面體[4],然而由於這個立體同時具備半多面體的特性,因此被部分學者分成一類新的立體,即擬正半多面體(Versi-Regular Polyhedra),這類立體共有九個,最早在1881年由亞伯特·巴杜羅(Albert Badoureau)發現並描述[5]。特別地,大十二面半二十面體的外接球的半徑正好是邊長的兩倍。[6]
性質
大十二面半二十面體由22個面、60條邊和30個頂點組成[7],每個頂點都是2個六邊形和2個五邊形的公共頂點,並且呈折四邊形狀排列,在頂點圖中,其可用6, 5/4, 6, 5來表示[8]。
對偶多面體
大十二面半二十面體的對偶多面體為大十二面半無窮星形二十面體[9]。其外觀與小十二面半無窮星形二十面體相同。[10][11]
相關多面體
大十二面半二十面體與截半大十二面體共用相同的邊排佈方式,因此可以視為是截半大十二面體經過刻面後的結果。[12]此外,小十二面半二十面體、截半大十二面體和大十二面半二十面體皆可以視為截半二十面体的刻面多面體。[13]
參見
參考文獻
Wikiwand - on
Seamless Wikipedia browsing. On steroids.